弹性地基梁法在箱涵中的应用

朱 涛 訾 娟 范瑞朋 武 帅

弹性地基梁法在箱涵中的应用

朱 涛 訾 娟 范瑞朋 武 帅

介绍了弹性地基梁计算的几种方法及适用条件，并根据实际工程选用了基床系数法计算了一个双孔箱涵的弯矩，并比较了弯矩分配法的计算结果。结果表明弹性地基梁法在箱涵的计算中更符合工程实际。

弹性地基梁 基床系数法 弯矩分配法 箱涵

1 弹性地基梁的简介

泵站、渡槽、水闸等水工建筑物，常常为了适应地基的不均匀沉降或者地基承载力的要求而采用大体积的混凝土基础。这种大体积的基础板梁结构，与地基有良好地接触，而且由于地基具有弹性，常称之为弹性地基梁[1]。地基的稳定是整个建筑物安全的关键，因此，弹性地基梁的结构设计非常重要。

弹性地基梁的底面与地基接触良好，当梁在上部荷载作用下变形时，地基随着梁的变形而变形，为多次超静定结构，不同于一般连续梁的刚性支座下的有限次静定结构。

2 弹性地基梁的计算假定

弹性地基梁与地基连续接触，梁所受的地基反力亦为连续分布的，为无穷多次超静定结构[2]，用常规静定结构的计算方法无法计算出弹性地基梁的内力和弯矩，需采用一定的假设来简化计算。目前，需根据不同的地基情况，常采用的计算假定有3种：（1）地基反力直线分布的假定；（2）文克尔假定（反力强度与沉降量成正比的假定）；（3）半无限理想弹性体的假定。

2.1 反力直线假定

反力直线假定是一种比较简单的假定计算方法，假定地基反力是呈直线分布的，在均布荷载的作用下呈矩形分布，在偏心荷载的作用下呈梯形分布，再根据静力平衡条件计算梁的内力和弯矩。

由于地基变形通常不是直线分布，多是近似直线的曲线分布，即基础与地基之间有变形协调，而且地基的土壤特性未被考虑其中，因此，是一种近似的计算方法。反力直线法的计算结果不够准确，但是计算简便易行，适用于一般的小型基础的计算和对大型基础的近似估值。

2.2 基床系数假定 （也称基床系数法）[3]

在基床系数假定中，考虑到了地基和建筑物基础之间的变形协调，将地基模拟为建筑物基础底座上的一系列独立的弹簧，弹簧既有刚度又有弹性。这样，地基的变形和建筑物基础的变形即为一致，较反力直线法地基变形更加切合实际。基床系数法的关键是弹簧的弹性系数需符合地基的实际，同时还应注意地基只能抵抗压力的作用[4]。

假定建筑物地基的变形y与地基每单位所承受的荷载N成正比，即N=ky，其中k为弹簧的弹性系数，即为基础的基床系数，此假定适用任何基础梁[5]。

虽然基床系数法应用范围较广，但是也存在一定的局限性：（1）由于弹簧只存在于建筑物基础底面，故基础荷载作用下的地基变形只发生在基础底部的地基范围内，基础以外的地基变形等于0。这显然是不合理的。地基的变形在建筑物基础边缘应该也是渐变的，基础区域外的地基变形应随着离建筑物的距离加大逐渐趋近于0。所以，这种假设对于变形较大，密实厚土层和重要的大型工程的地基，会产生较大误差。（2）基床系数法的另外一个局限就是基床系数的选取。基床系数不仅与土壤的性质有关，而且还与荷载的大小和基础形状有关，故基床系数选取的主观因素较多，需要有丰富的工程经验。

2.3 半无限理想弹性体的假定

半无限地基假定的原则是：地基为均匀、连续、弹性的半无限体。因此，可以用弹性理论中的公式来计算地基反力，从而计算建筑物基础的受力和弯矩。

目前基于半无限弹性地基假定的近似解决方法有：多项式法、链杆法、能量法等[5]。无论哪种方法的计算都是一个繁琐的过程，所以，在实际计算中，已有前人根据不同的荷载工况，建立了一些相关的计算参数表格[6]，例如郭氏表，可查表获得相关参数，从而简化计算。

由于土壤并不是匀质弹性体，而且土壤的变形不止包括弹性变形，受力较大时，还会产生塑性变形，因此，把土壤当作半无限的弹性体，也存在一定的局限性。只有当地基为厚状整块的岩层或者厚度远大于基础的水平尺寸土层时，才能近似为半无限体弹性地基[1]。

3 弹性地基梁的计算实例及比较

本文所用工程实例为天津独流减河右堤加固工程中的一个箱涵。该箱涵为双孔矩形箱涵，为三级建筑物，涵底位于地下水位以上。涵底为夯实的砂土地基，相对密度为0.8，压缩模量Es=62 000 kN/m2；涵顶填土高度3.5 m，填土容量18.1 kN/m3，内摩擦角为32°。涵孔净高H=3.0 m，净宽3.5 m，底板厚度d1=0.40 m，顶板厚度d2=0.35 m，侧墙和中墙厚度d3=0.3 m。箱涵尺寸和各节点编号见图1。本次计算只计算箱涵完建工况，即涵内外均无水的工况。

图1 箱涵剖面尺寸及受力计算简图

本次箱涵计算比较弯矩分配法和弹性地基梁法的计算结果。

3.1 弯矩分配法

弯矩分配法的计算方法是按结点及杆端列表依次对各结点进行弯矩分配和传递，以消除各结点的不平衡弯矩。计算过程：首先计算该结点各杆端的固端弯矩代数和，将该代数和反号，分别乘各杆端的分配系数得各杆端的分配弯矩，各分配弯矩乘以相应的传递系数传至远端，各节点轮流传递，直至满足精度要求；最后将固端弯矩、分配弯矩和传递弯矩叠加得到杆端总弯矩。

根据SL 191—2008《水工混凝土结构设计规范》的要求和 《涵洞》 （中国水利水电出版社）的计算公式，可得箱涵各部位受力情况，详见图1。作用于顶板的垂直均布荷载q2=84.45 kN/m，包括涵洞顶部土重和涵洞顶板的重量；作用于底板上的垂直均布荷载总和q1=93.42 kN/m，为q2与侧墙及中墙产生的地基反力之和；q3和q4为作用在侧墙面上的土压力，q3=43.08 kN/m，q4=22.45 kN/m。

经计算，弯矩分配法计算得到的箱涵弯矩图见图2。

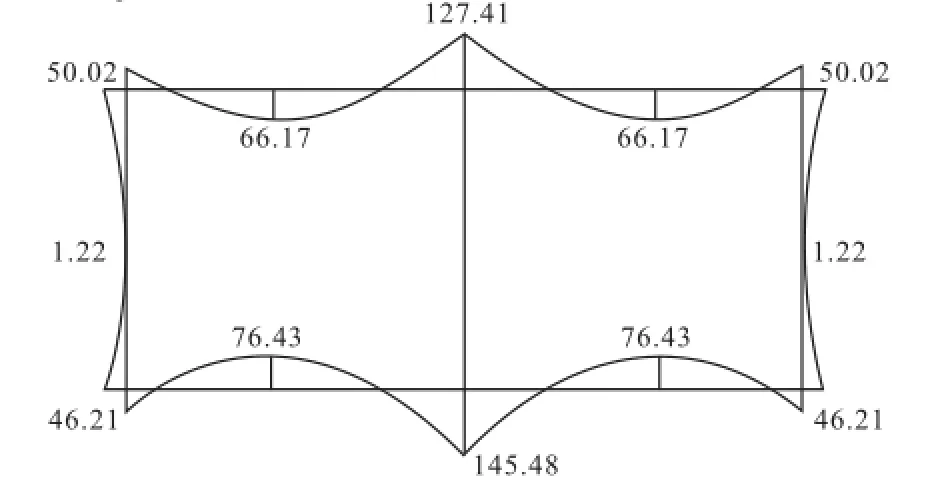
图2 弯矩分配法计算弯矩图 （单位：kN·m）

3.2 弹性地基梁法

涵底为夯实的砂土地基，相对密度为0.8，适宜用弹性地基梁法计算箱涵的弯矩。由于可压缩土层厚度与弹性地基梁半长的比值小于0.25，可选用弹性地基梁法中的基床系数法。

侧墙上的土压力q3和q4可见图1；作用于顶板的垂直均布荷载q2=75.26 kN/m，为涵洞顶部土重 （不计涵洞顶板的重量）；作用于底板上的垂直均布荷载q1由弹簧取代。由于箱涵受对称荷载，所以在D点 （见图1）固定箱涵横向位移，在箱涵底部加弹簧。以上操作可在SAP2000结构软件中进行。

根据中国船舶工业总公司第九设计研究院编写的 《弹性地基梁及矩形板计算》附录5，密实砂土的基床系数取值范围为50 000～10 000 kN/m3，参考已有工程经验和地基的压缩模量，本次计算取60 000 kN/m3，本次计算取单位长度的箱涵，弹簧间距取1.0 m，所以弹簧的刚度取60 000 kN/m。

经计算，弯矩分配法计算得到的箱涵弯矩图见图3。

图3 基床系数法计算弯矩图 （单位：kN·m）

3.3 计算结果分析

根据弯矩分配法和基床系数法计算得到箱涵各关键部位弯矩值，详见表1。

表1 两种计算方法弯矩值比较表 kN·m

其中，弯矩MBA=MBD，MAB=MAC，表中不一一列出。

由表1可知，弯矩分配法和弹性地基梁法计算得到的弯矩值都较接近，特别在箱涵顶部区别较小，但是两种方法在箱涵底部计算结果区别较大，弹性地基梁法计算得到的底部弯矩图较平缓，说明弹簧对箱涵底部地基变形起到了协调作用。弹性地基法计算结果更加接近实际，能较好地应用于工程之中。

[1]李涛.浅谈弹性地基梁法在水闸底板设计中的应用 [J].河南水利与南水北调,2013(2)：32-34.

[2]龙驭球.弹性地基梁的计算[M].北京：高等教育出版社，1983.

[3]中国船舶工业总公司第九设计研究院.弹性地基梁及矩形板计算[M].北京：国防工业出版社，1983.

[4]彭俊生，罗永坤.结构概念分析与SAP 2000应用[M].成都：西南交通大学出版社，2005.

[5]卢晓莉，李琦.弹性地基梁的计算方法[J].枣庄师专学报，2008，25 (2):68，70.

[6]李云勋，朱振凯.弹性地基梁郭氏查表法和链杆法计算特点的比较 [J].科技资讯，2012(23):46，48.

朱 涛 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222

訾 娟 女 工程师 中水北方勘测设计研究有限责任公司 天津 300222

范瑞朋 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222

武 帅 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222

TV222.2

B

1007-6980（2016）02-0007-03

（2016-03-25）