时变参数比例自适应滤波算法
倪锦根
(苏州大学电子信息学院,江苏苏州 215006)
时变参数比例自适应滤波算法
倪锦根
(苏州大学电子信息学院,江苏苏州 215006)
在免提电话和视频会议系统中,自适应滤波器估计的回声路径通常是稀疏的.改进的比例归一化最小均方(IPNLMS)算法能够加快自适应滤波器在估计稀疏系统时的收敛速度,但与归一化最小均方(NLMS)算法相比,其稳态失调的波动性较大.为了解决这一问题,本文提出了一种时变参数IPNLMS(TV-IPNLMS)算法.该算法根据系统的均方误差(MSE)与噪声功率的比值,使用一个sigmoid函数来调整时变参数的值.该时变参数能够降低IPNLMS算法在滤波器到达稳态时的比例增益.仿真结果表明,时变参数方法能够降低IPNLMS算法稳态失调的波动性.该算法可用于回声消除、主动噪声控制等领域.
免提电话;视频会议;比例自适应;时变参数;稳态失调
1 引言
自适应滤波技术在通信、雷达、声纳等领域获得了广泛应用[1].自适应滤波算法决定了自适应滤波器的收敛速度和稳态失调.最小均方(LMS)算法及其改进算法[2]和归一化最小均方(NLMS)算法及其改进算法[3]是两类重要的自适应滤波算法.在网络和声学回声消除等应用中,待估计的回声路径脉冲响应通常是稀疏的,即回声路径脉冲响应只有很少系数的值较大,而大部分系数的值很小或者为零[4].如果采用LMS或NLMS算法来估计稀疏系统,则收敛较慢.
Duttweiler于2000年提出了著名的比例NLMS(PNLMS)算法[5].该算法根据回声路径脉冲响应的稀疏性,给自适应滤波器的每个系数按比例分配增益,从而加快自适应滤波器在估计稀疏系统时的收敛速度.然而,当待辨识的系统是非稀疏时,PNLMS算法比NLMS算法收敛更慢.为了保证PNLMS算法在估计非稀疏系统时仍然保持较快的收敛速度,Benesty等人提出了一种改进的PNLMS(IPNLMS)算法[6].无论待估计系统是稀疏还是非稀疏的,IPNLMS算法的收敛速度都优于PNLMS算法.在IPNLMS算法被提出之后,许多比例自适应算法采用了IPNLMS算法中使用的增益分配思想,如文献[7~9].通过仿真实验可以发现,在估计稀疏系统时,IPNLMS算法的收敛速度快于NLMS算法,但其稳态失调的波动性较大.在回声消除等应用中,大的稳态失调波动性会在免提电话、视频会议等设备中产生严重的干扰噪声,从而影响通话质量[10,11].文献[12]提出了一种变参数IPNLMS(VP-IPNLMS)算法,该算法能够加快滤波器估计非稀疏系统时的收敛速度,但在估计稀疏系统时,其稳态失调的波动性仍然较大.
针对上述问题,本文提出了一种时变参数方法来降低IPNLMS算法稳态失调的波动性.该方法根据系统的均方误差与噪声功率的比值,使用一个sigmoid函数来自动调整时变函数的值.仿真结果表明,本文提出的时变参数方法,能够显著减小IPNLMS算法引起的稳态失调波动性.
2 时变参数IPNLMS算法
在自适应滤波应用中,通常认为期望响应d(n)满足模型
d(n)=uT(n)wo+v(n)
(1)
其中,(·)T表示转置运算符,u(n)=[u(n),u(n-1),…,u(n-M+1)]T表示由输入信号的M个样值构成的输入向量,wo为待估计系统的脉冲响应,v(n)为系统噪声.通常假设u(n)、v(n)和d(n)的均值为零.若均值不为零,可对其进行预处理[1].
令w(n)=[w0(n),w1(n),…,wM-1(n)]T为自适应滤波器在n时刻的系数向量,μ为步长参数,δ为很小的正则化参数,e(n)为误差信号且满足
e(n)=d(n)-uT(n)w(n)
(2)
则IPNLMS算法的迭代公式可表示为[6]
(3)
其中,G(n)表示M×M的对角增益矩阵.该矩阵的第m个对角元素由下式确定

m=0,1,…,M-1
(4)
其中,‖w(n)‖1表示系数向量w(n)的l1范数,ε为很小的正常数,α为在区间[-1,1)内取值的参数.
IPNLMS算法给自适应滤波器的每个系数按比例分配增益.当自适应滤波器处于稳态阶段时,大的系数仍然采用大的增益进行更新,导致IPNLMS算法比NLMS算法的稳态失调的波动性更大.本文采用如下方法来解决这一问题:在自适应滤波初始阶段,给式(4)中的参数α分配一个较大的值,使得自适应滤波器按照IPNLMS算法进行迭代,从而获得较快的收敛速度;在自适应滤波稳态阶段,使参数α的值趋于-1,使得IPNLMS算法性能接近NLMS算法,从而降低稳态失调的波动性.为了达到上述目的,我们将参数α变为时变的参数α(n),从而式(4)可改写为
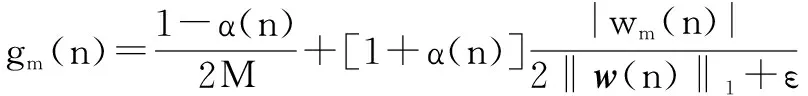
m=0,1,…,M-1
(5)
本文将采用式(5)的IPNLMS算法称为时变参数IPNLMS(TV-IPNLMS)算法.下面来讨论α(n)的选取问题.
定义自适应滤波器的含噪信噪比为
(6)
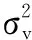
误差信号e(n)的大小能较好地反应自适应滤波器所处的阶段,因而可以通过建立α(n)和e(n)之间的关系来自动更新α(n)的值.为此,定义如下的中间变量
(7)

当自适应滤波器处于0时刻时,根据式(2)和常用的初始条件w(0)=0,可得E[e2(0)]=E[d2(0)],从而有
x(0)=NSNR/10
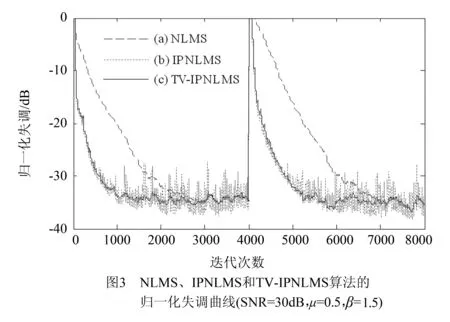
(8)
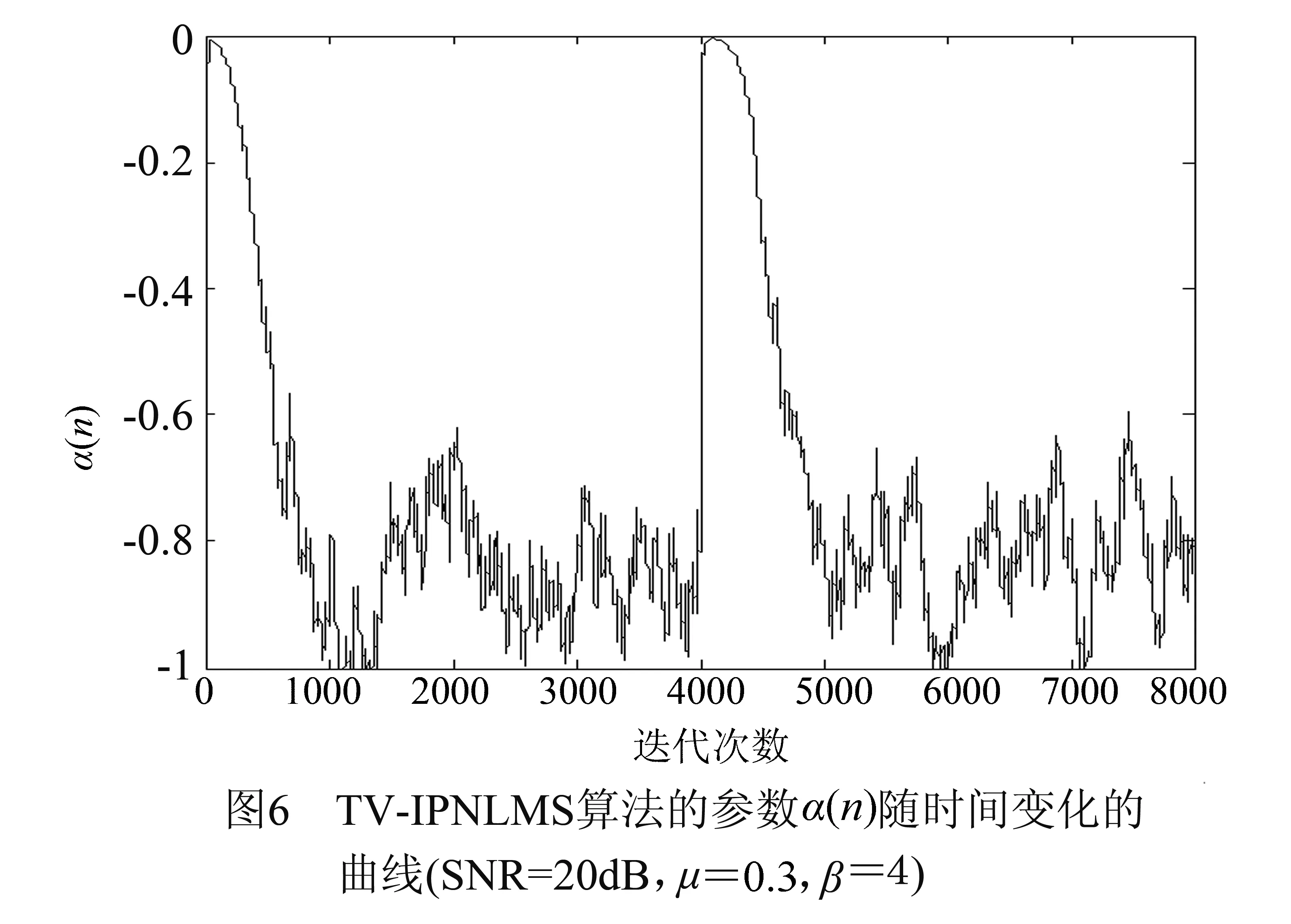
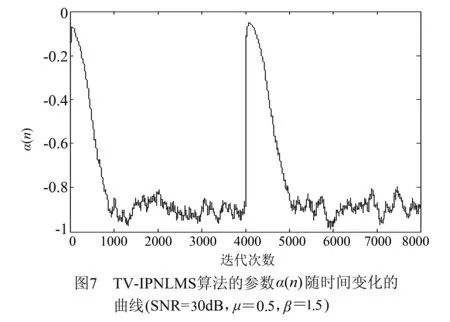
在平稳信号输入下,E[e2(n)]随着迭代次数增大逐渐而减小,从而有E[e2(n)] (9) 对于NLMS算法,当自适应滤波器处于稳态时,即n→∞,其稳态均方误差为[1] (10) 上式随步长参数变化的极限值为 (11) 假设α(n)在稳态阶段能取到近似-1的值,则TV-IPNLMS算法近似于NLMS算法,从而式(11)也是TV-IPNLMS算法稳态均方误差的下限.将式(11)代入式(7),可得 (12) 综合式(8)、(9)和(12),可得 0≤x(n) (13) 将待估计系统的无噪声输出信号记为y(n)=uT(n)·wo,则通常意义下的信噪比(SNR)的定义为 (14) 虽然e(n)能够反应自适应滤波器所处的阶段,但是在不同的输入信号和噪声环境中,e(n)的差别较大.为此,选择一个与e(n)相关但是在不同环境中差别较小的变量更为重要.一个较好的选择就是SNR,因为在大部分应用中,SNR位于区间[10,80]内,其典型值位于10至40之间.因此,在典型信噪比环境中,有E[d2(n)]≈E[y2(n)],从而有NSNR≈SNR.根据式(13)可知,在不同的输入信号和噪声环境中,式(7)中x(n)的取值范围要远小于e(n)的取值范围.此外,x(n)的最小值为0,而e(n)的最小值随着输入信号和噪声的不同而不同.因此,采用x(n)来估计自适应滤波器的工作状态要优于采用e(n). 中间变量x(n)选定之后,还需要选择关于x(n)的单调递增函数.在众多函数中,S型的sigmoid类函数在线性和非线性之间实现了很好的平衡,并且其形状可以通过调整斜率参数来改变.一个应用广泛的sigmoid类函数是logistic函数,其表达式为[16] f(t)=1/[1+exp(-βt)] (15) 其中β为logistic函数的斜率参数,该参数控制logistic函数的形状.取不同斜率参数的logistic函数如图1所示.由该图可见,f(t)在0到1之间取值,其对称中心位于点(0,0.5). 令φ为时变参数α(n)的上限,则该上限应满足条件φ∈[-1,1),且α(n)的下限应为-1.因此,α(n)与式(15)中的f(t)取值范围和对称中心均不相同.为了获得满足条件的时变参数α(n),需要将式(15)中的logistic函数进行缩放和平移,具体过程如下:将f(x(n))放大2φ+2倍后,再将放大后的函数沿着纵轴向下平移φ+2,可得 (16) 容易验证,在x(n)≥0和φ∈[-1,1)条件下,式(16)中的α(n)位于区间[-1,1)内,该区间与IPNLMS算法中参数α要求的取值范围相同. TV-IPNLMS算法的性能会受到logistic函数的斜率参数β的影响,该参数的取值主要依赖于环境的SNR、待估计系统的脉冲响应长度以及输入信号的统计特征,其选取原则如下:(1)在低SNR环境中,大的噪声功率会使得x(n)取值较小,α(n)的取值也相应减小,导致自适应滤波器在估计稀疏系统时收敛较慢.因此,在低SNR环境中,应该选择较大的β值,来补偿x(n)对时变参数α(n)取值的影响,从而维持自适应滤波器在估计稀疏系统时的收敛速度.在高SNR环境中,自适应滤波器的收敛速度受噪声影响不大,因此可以使用较小的β值来获得尽可能小的稳态失调波动性.(2)对于较长的脉冲响应或者相关性较高的输入信号,由于自适应滤波器在达到稳态前,具有较长的过渡阶段,β可以取较大的值来加快自适应滤波器的收敛速度.对于较短的脉冲响应或相关性较小或不相关的输入信号,自适应滤波器收敛较快,β可以取较小的值来获得尽可能小的稳态失调波动性. 本节通过计算机仿真来比较NLMS[1]、IPNLMS[6]、VP-IPNLMS[12]和本文提出的TV-IPNLMS算法在估计稀疏系统时的稳态失调波动性.待估计系统具有100个系数,除4个系数外,其他系数的值均为零,4个非零系数位于点{1,30,35,85}处,其对应的值为{0.1,1.0,-0.5,0.1}.输入信号u(n)为二阶自回归(AR)随机过程,由零均值的高斯白噪声θ(n)通过系统u(n)=0.40u(n-1)-0.40u(n-2)+θ(n)产生.系统噪声采用零均值的高斯白噪声.上述条件与文献[17]中的仿真条件相似.IPNLMS算法的参数α取为0,相应地,TV-IPNLMS算法的时变参数α(n)的上限φ亦取为0.估计误差信号功率的平滑因子λ取为0.99.为了比较算法的跟踪性能,在算法运行到第4000点时,将待估计系统的脉冲响应向右循环平移12个样值.采用归一化失调作为衡量算法性能的指标,其定义为ρ(n)=20log10‖wo-w(n)‖/‖wo‖,单位为分贝(dB)[18]. 图2比较了NLMS、IPNLMS和TV-IPNLMS算法在20dB信噪比环境下的归一化失调曲线.三种算法的步长均取为μ=0.3.TV-IPNLMS算法的斜率参数取为β=4.由图2可见,IPNLMS和TV-IPNLMS算法比NLMS算法收敛更快,且TV-IPNLMS算法比IPNLMS算法的稳态失调波动性更小.图3通过将信噪比增加到30dB来比较三种算法的归一化失调曲线.三种算法的步长均取为μ=0.5.根据TV-IPNLMS算法斜率参数选取原则,在相同输入信号作用下,信噪比越高,β的取值越小.因此,在30dB信噪比环境下,TV-IPNLMS算法的斜率参数取为β=1.5.由图3可见,TV-IPNLMS算法仍然优于NLMS和IPNLMS算法. 图4和图5分别比较了VP-IPNLMS和TV-IPNLMS算法在20dB和30dB信噪比环境下的归一化失调曲线.TV-IPNLMS算法的参数在不同信噪比环境下的取值分别与图2和图3相同.由于自适应滤波器的初始权值取为w(0)=0,VP-IPNLMS算法无法根据公式计算稀疏度.为此,本文在VP-IPNLMS算法计算稀疏度的公式中加入了很小的正常数,用来防止数值计算困难.由图4和图5可见,在估计实验中使用的稀疏系统时,TV-IPNLMS算法比VP-IPNLMS算法的稳态失调波动性更小. TV-IPNLMS算法的优越性源于参数α(n)的自动调整.图6和图7分别给出了TV-IPNLMS算法的参数α(n)在20和30dB信噪比环境下随时间变化的曲线.由图6和图7可见,在自适应滤波的初始收敛阶段,参数α(n)取值较大;随着迭代的进行,参数α(n)的取值逐渐减小;在稳态阶段,参数α(n)的取值在最小值-1上方波动,且信噪比越大,波动越小.因此,参数α(n)随时间自动调整的过程符合比例增益取值的要求. IPNLMS算法在估计稀疏系统时比经典的NLMS算法收敛更快,但其稳态失调的波动性较大.本文提出了一种时变参数IPNLMS算法来解决上述问题.该时变参数IPNLMS算法根据系统的均方误差与噪声功率的比值来调整时变参数的值,从而达到自动调整比例增益的目的.仿真结果表明,在估计稀疏系统时,时变参数IPNLMS算法稳态失调的波动性远小于IPNLMS算法. [1]Sayed A H.Adaptive Filters[M].Hoboken,NJ:John Wiley & Sons,2008. [2]洪丹枫,苗俊,等.一种变步长凸组合LMS自适应滤波算法改进及分析[J].电子学报,2014,42(11):2225-2230. HONG Dan-feng,MIAO Jun,et al.An improved variable step-size convex combination of LMS adaptive filtering algorithm and its analysis[J].Acta Electronica Sinica,2014,42(11):2225-2230.(in Chinese) [3]刘立刚,FUKUMOTO Masahiro,张世永.一种变步长proportionate NLMS自适应滤波算法及其在网络回声消除中的应用[J].电子学报,2010,38(4):973-978.LIU Li-gang,FUKUMOTO Masahiro,ZHANG Shi-yong.A variable step-size proportionate NLMS adaptive filtering algorithm and its application in network echo cancellation[J].Acta Electronica Sinica,2010,38(4):973-978.(in Chinese) [4]文昊翔,陈隆道,蔡忠法.改进仿射投影算法及其在电子回声消除中的应用[J].电子学报,2012,40(6):1229-1234. WEN Hao-xiang,CHEN Long-dao,CAI Zhong-fa.An improved affine projection algorithm and its application in network echo cancellation[J].Acta Electronica Sinica,2012,40(6):1229-1234.(in Chinese) [5]Duttweiler D L.Proportionate normalized least-mean-squares adaptation in echo cancellers[J].IEEE Transactions on Speech and Audio Processing,2000,8(5):508-518. [6]Benesty J,Gay S L.An improved PNLMS algorithm[A].IEEE International Conference on Acoustic,Speech,and Signal Processing[C].Piscataway,New Jersey:IEEE Press,2002.1881-1884. [7]Paleologu C,Ciochina S,Benesty J.An efficient proportionate affine projection algorithm for echo cancellation[J].IEEE Signal Processing Letters,2010,17(2):165-168. [8]Yang Z,Zheng Y R,Grant S L.Proportionate affine projection sign algorithms for network echo cancellation[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(8):2273-2284. [9]Burton T G,Goubran R A.A generalized proportionate subband adaptive second-order Volterra filter for Acoustic Echo Cancellation in Changing Environments[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(8):2364-2373. [10]Paleologu C,Benesty J,and Ciochina S.Study of the general Kalman filter for echo cancellation[J].IEEE Transactions on Audio,Speech,and Language Processing,2013,21(8):1539-1549. [11]Paleologu C,Benesty J,Ciochina S.Widely linear general Kalman filter for stereophonic acoustic echo cancellation[J].Signal Processing,2014,94(1):570-575. [12]Liu L,Fukumoto M,Zhang S.A variable parameter improved proportionate normalized LMS algorithm[A].IEEE Asia Pacific Conference on Circuits and Systems[C].Piscataway,New Jersey:IEEE Press,2008.201-204. [13]Benesty J,Rey H,et al.A nonparametric VSS NLMS algorithm[J].IEEE Signal Processing Letters,2006,13(10):581-584. [14]Ni J,Li F.Varable step-size matrix normalized subband adaptive filter[J].IEEE Transactions on Audio,Speech,and Language Processing,2010,18(6):1290-1299. [15]Paleologu C,Ciochina S,Benesty J.Variable step-size NLMS algorithm for under-modeling acoustic echo cancellation[J].IEEE Signal Processing Letters,2008,15(1):5-8. [16]Haykin S.Neural Networks and Learning Machines[M].Upper Saddle River,NJ:Prentice-Hall,2009. [17]Souza F C de,Tobias O J,et al.A PNLMS algorithm with individual activation factors[J].IEEE Transactions on Signal Processing,2010,58(4):2036-2047. [18]Ni J,Chen X,Yang J.Two variants of the sign subband adaptive filter with improved convergence rate[J].Signal Processing,2014,96(B):325-331. 倪锦根男,1979年11月生,江苏省兴化市人.毕业于复旦大学,获理学博士学位,现为苏州大学电子信息学院副教授、硕士生导师,IEEE会员.主要研究方向为自适应滤波、自适应网络、多采样率滤波器组设计、高速数字系统的FPGA实现. E-mail:jni@suda.edu.cn Time-Varying Parameter Proportionate Adaptive Filtering Algorithm NI Jin-gen (SchoolofElectronicandInformationEngineering,SoochowUniversity,Suzhou,Jiangsu215006,China) In hands-free telephones and teleconferencing systems,the echo path to be estimated by the adaptive filter is usually sparse.The improved proportionate normalized least-mean-square (IPNLMS) algorithm can increase the convergence rate of the adaptive filter when it is used to estimate sparse systems.However,the steady-state misalignment of the IPNLMS algorithm may suffer from much larger fluctuations than that of the normalized least-mean-square (NLMS) algorithm.To address this problem,a time-varying parameter IPNLMS (TV-IPNLMS) algorithm is proposed,which uses a sigmoid function to adjust the value of the time-varying parameter according to the ratio of the mean square error (MSE) to the power of the system noise.This time-varying parameter can reduce the proportionate gains of the IPNLMS algorithm when the adaptive filter arrives at steady state.Simulation results show that the time-varying parameter method can reduce the fluctuations of the steady-state misalignment of the IPNLMS algorithms.This algorithm can be used in the fields of echo cancellation,active noise control,and so on. hands-free telephone;teleconferencing system;proportionate adaptation;time-varying parameter;steady-state misalignment 2015-03-30; 2015-11-12;责任编辑:覃怀银 国家自然科学基金(No.61471251,No.61101217);江苏省自然科学基金(No.BK20131164) TN911.72 A 0372-2112 (2016)05-1208-05 电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.028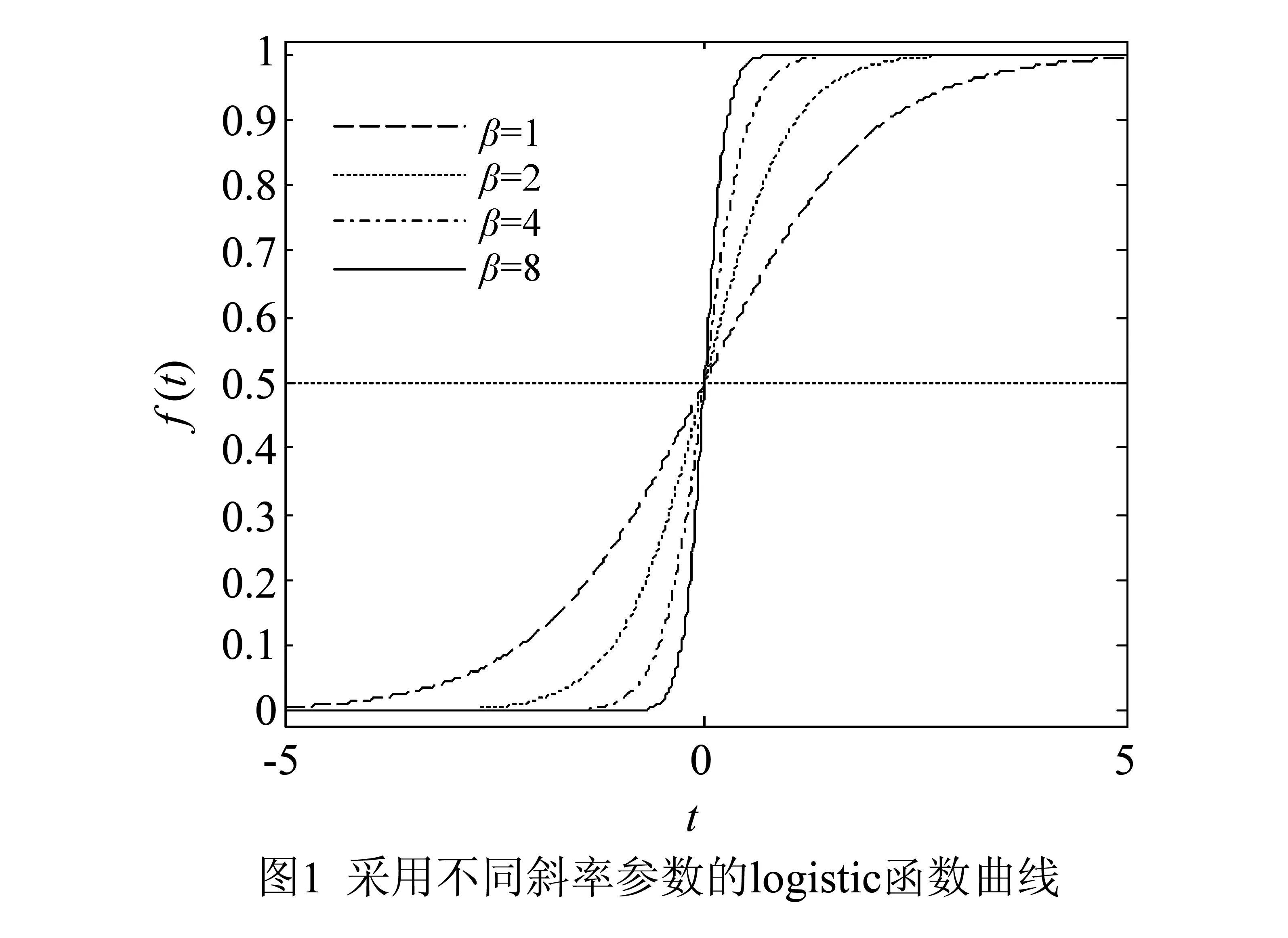
3 仿真实验



4 结论


