Stokes参数数字化求解的误差分析

陆　浩,王振占,刘璟怡,李　彬,董　帅

(中国科学院微波遥感技术重点实验室,中国科学院国家空间科学中心,北京 100190)



Stokes参数数字化求解的误差分析

陆浩,王振占,刘璟怡,李彬,董帅

(中国科学院微波遥感技术重点实验室,中国科学院国家空间科学中心,北京 100190)

Stokes参数是描述极化波的强度量纲,在电磁测量、合成孔径雷达、辐射计中均有广泛应用.文中提出了求解Stokes参数的数字化方法,具有带宽高、稳定性高等特点.针对将模拟信号采样量化后求解Stokes参数的方法,本文分别就自相关和互相关两种计算过程,详细分析并给出了数字量化对最终亮温的误差贡献.文中证明了高于3bit量化引入的亮温误差小于1*10-5K,进一步给出了量化后的系统灵敏度,分析了由数字量化产生的亮温灵敏度偏差.当量化位数为3bit时,数字相关系统灵敏度可以达到理想模拟相关系统的95%.本文为不同应用条件下,满足不同精度时,如何选择特定量化位数与量程提供了依据.

Stokes参数;相关计算;数字采样;量化误差

1　引言

为了描述电磁波的极化状态,1852年英国物理学家Stokes提出用四个具有强度量纲的参数来描述极化波,称之为Stokes参数,如式(1)所示[1]:

(1)

其中,Ev、Eh分别为垂直和水平方向的电场强度,η为波阻抗,k是波尔兹曼常数,λ是波长.

Stokes参数表示了目标电磁辐射的极化度,在电子与光子符合散射实验中,通过测量光子的Stokes参数可以描述受激P态电荷云分布和散射过程的动力学[2].极化电子束在物理学及其相关领域应用十分广泛,要深入研究这些应用必须对电子束的极化度进行精确测量,即对Stokes参数的精确测量[3].此外,Stokes参数归一计算在空间探测望远镜得图像预处理中有重要意义[4].

Stokes参数在合成孔径雷达(SAR)中有重要应用.SAR标准化Stokes参数分布的概率密度函数描述了SAR多视图像的随机状态特性,这对地表目标识别具有重要意义.而在全极化辐射计中,求解Stokes参数可以反演海面风场.Stokes参数的复相关分量T3和T4是表征目标特性的重要参数,T3主要表征线性极化的程度,而T4表征极化方向性的特征,且不受Faraday旋转的影响,对大气中的水汽和液水不敏感,更适合在各类天气观测海面风向.

由式(1)可知,可以通过求解单个信号自相关和两个信号互相关来得到Stokes参数.Stokes参数的数字化是指通过将极化信号采样量化后再进行相关计算.将模拟信号采样、量化、编码是数字处理的前提,而数字化的过程引入的噪声和非线性也直接影响着系统的性能[5],因此需要对数字化过程做详细分析,验证数字化方法的可行性.下面分别给出了量化对四个stokes参数计算结果的影响,并分析量化误差对所测亮温灵敏度的影响.

2　数字采样

采样是利用模数转换器(ADC)把连续时间信号转化成离散时间信号,而采样必然带来偏差,输入信号x(t)取均值为零的高斯随机噪声模型,方差为σ2,密度函数为:

(2)

ADC步进为v,量化电压Vadc和量化阶数的关系如下式:

Vadc=a*σ=2wv

(3)

高斯噪声超过99%的信号落在6σ以内,我们的实际应用中a略大于6.w表示量化位数,s可以表示为:s=2w/a.

实际的AD采样会同时引入量化偏差和非线性偏差,定义ΔV为总的量化误差,量化偏差为ΔVq其限制在-v/2到v/2,非线性偏差ΔVL为λv/2,其中λ取值范围为(-1,1),反映了AD与理想线性量化的偏离程度.非线性偏差可以理解成在量化偏差的基础上叠加的误差.量化偏差和非线性偏差都是AD采样过程中需要带入分析的误差源.

ΔV=ΔVq+ΔVL

(4)

ΔVq与ΔVL是误差分析中不可缺少的研究对象.定义ΔV归一化量化偏移为:

b=ΔV/v

(5)

3　量化误差

3.1Tv、Th量化误差

如图1所示为自相关情况下的原理框图,X(t)表示V或H极化通道进入ADC前的信号.X(t)采样后求平方然后累加,输出为rQ,而如果不经过量化处理,理想化模拟的输出为r∞.

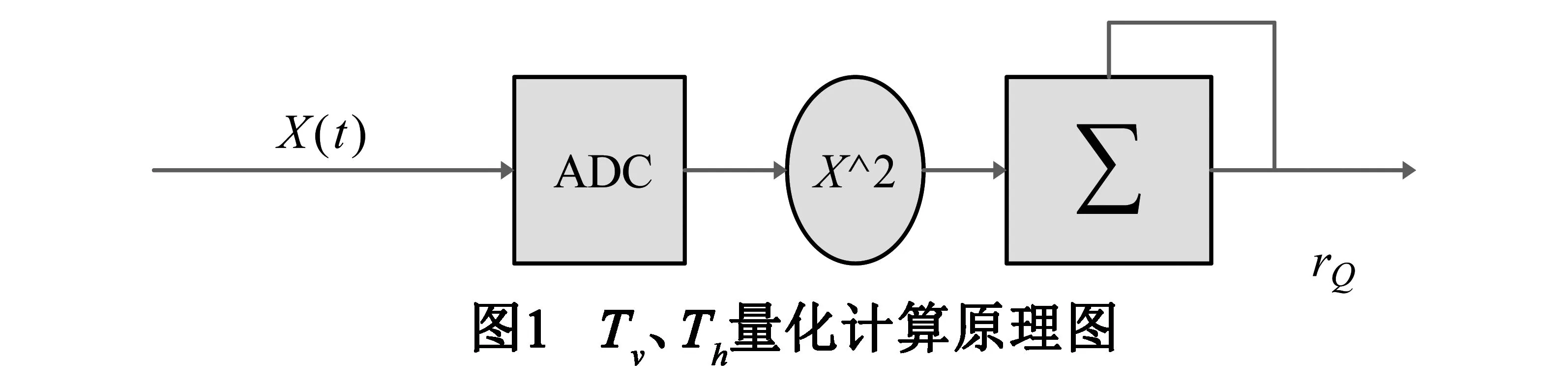
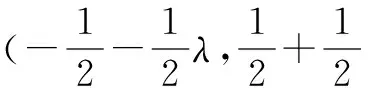
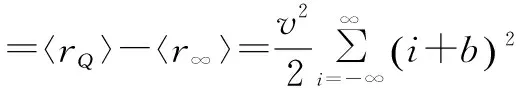
(6)

〈re〉为有限量化和无限量化的输出差值.当s在0.7以下时,〈re〉呈现明显的变化趋势,而当s大于1时,量化偏差则稳定在v2/12+λ2v2/16.目前通用的ADC的量化位数基本都在3bit以上,其s均大于1,λ均小于1%.以10bit(1024阶)量化的ADC为例,假设量程为1000mv,则其步进0.98mv,在阻抗匹配50欧姆的系统,引入噪声功耗小于-40dBm.这样因量化引入的误差就可以忽略.以上结论定量说明了可以忽略多位量化在Stokes第一参数、第二参数计算中产生的误差.

3.2T3、T4量化误差

根据式(1),T3、T4为两个极化通道之间的互相关结果,在实际数字量化以后就是两个数字量乘积的均值.图2为两路信号互相关的数字化过程,x(t)表示V通道进入ADC之前的噪声信号,y(t)表示H通道进入ADC之前的噪声信号.第三stokes参数为互相关的实部rreal,是x(t)与y(t)信号被采样成离散数列后相乘累加后的值.第四stokes参数为互相关的虚部rimag,是y(t)信号移相90°之后与x(t)信号被采样成离散数列后相乘累加后的值.

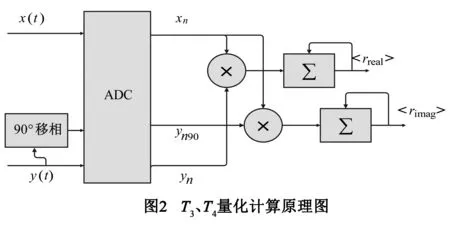
第三与第四个stokes参数的输出结果均可以写成x、y组合的权重形式,如下:

(7)

其中,b1和b2是相关通道的量化偏差,实际应用中,多个通道的采样一般都在一片ADC中完成,此时量化偏移b1与b2可以认为是一致的,因此上式可以简化为:

(8)

(9)

则:

〈rreal/imag〉=

(10)

图3为式(10)加号左右两边随s值的变化曲线,采用离散的形式直观表现.左函数在b取1/4时最大,随着s的增加而递减,当s在0.6以上时,左函数的最大值小于2.1e-007,可以证明对于多位量化来说,左函数近似为0.同样,当s大于0.7的时候,右函数的最大值接近ρσ2,误差在1e-005以内,因此当s大于0.7时,可以得到rreal/imag=ρσ2.

以上结论定量证明了可以忽略多位量化在Stokes第三参数、第四参数计算中产生的误差.

4　数字量化灵敏度

4.1Tv、Th亮温灵敏度

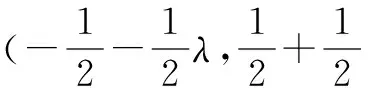
(11)

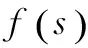
(12)

因为〈r∞〉是定值,所以〈re〉和〈rQ〉具有相同的标准偏差:

(13)

输出的信噪比定义为:

(14)

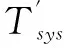
TQ=v2/12+λ2v2/16

又由上述结论可知,下式成立:

〈rQ〉≈σ2+v2/12+λ2v2/16

(15)

综合可知:

(16)

灵敏度影响为:

(17)

4.2T3、T4亮温灵敏度

在互相关的情况下,相关输出rreal/imag的方差为:

(18)

其中,N=2Bτ,τ是积分时间,B是中频带宽.对式(18)的第一项做分解[7]:

(19)

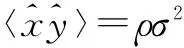
(20)

x、y的自相关函数,表示如下[8]:

(21)

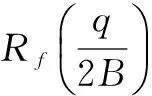
(22)

将式(22)与式(20)代入式(18),得到:

(23)

其中的s因子充分说明了数字量化给互相关的亮温灵敏度带来的影响.当量化位数为3bit时,根据式(3),s值等于1.48,而λ通常小于1%,因此数字相关系统灵敏度可以达到理想模拟相关系统的95%以上.在假设采样位数足够高(s趋于∞),且AD具有理想的线性化特征,式(23)又简化为:

这就是理想的模拟复相关灵敏度.

5　总结

Stokes在科学理论研究和工程应用中有着广泛的意义.文中分析了数字化方法求解Stokes参数的误差,定量给出了采样及非线性对理想值的影响.Stokes参数计算包含自相关和互相关计算.文中计算了量化分别对四个stokes参数引入的亮温误差,证明在实际应用中其值小于1*10-5K,进一步给出了量化下的系统灵敏度,分析了由数字量化产生的灵敏度误差.当量化位数为3bit时,数字相关系统灵敏度可以达到理想模拟相关系统的95%.本文为不同应用条件下,满足不同精度时,如何选择特定量化位数与量程提供了依据和标准.通过误差值,说明了多位数字量化引入的误差相对于理想值可以忽略.随着数字化技术的发展,5GHz以上采样率的ADC以及1GHz以上主频率的集成芯片已经市场化,这都超过模拟相关处理器的带宽,数字化具有广阔的前景.

[1]王振占,姜景山,刘憬怡,殷晓斌.全极化微波辐射计遥感海面风场的关键技术和科学问题[J].中国工程科学,2008,12(10):76-86.WANGZhen-zhan,JIANGJing-shan,LIUJing-yi,YINXiao-bin.Keytechniquesandscientificissuesofthesurfacewindfieldinthefullypolarimetricmicrowaveradiometer[J].EngineeringSciences,2008,12(10):76-86.(inChinese)

[2]刘义保,庞文宁,丁海兵,尚仁成.原子受激态的Stokes参数分析[J].原子核物理评论,2005,22(3):300-308.

LIUYi-bao,PANGWen-ning,DINGHai-bing,SHANGRen-cheng.AnalysisofStokesparametersinatomicstateexcitedbyelectrons[J].NuclearPhysicsReview,2005,22(3):300-308.(inChinese)

[3]李兴鳌,阮存军,等.光学极化度测量仪的研制及弱光Stokes参数的测量[J].物理,2000,29(12):742-745.LIXing-ao,RUANCun-jun,etal.DevelopmentofopticalelectronpolarimetryandmeasurementofweaklightStokesparameters[J].Physics,2000,29(12):742-745.(inChinese)

[4]王宇舟,金声震.空间太阳望远镜的图象预处理系统研制[J].电子学报,2005,33(7):1291-1294.

WANGYu-zhou,JINSheng-zhen.Developmentofimagepreprocessingsystemforspacesolartelescope[J].ACTAElectronicaSinica,2005,33(7):1291-1294.(inChinese)

[5]马仑,廖桂生,杨鹏,明洋.一种新的并行交替采样系统误差估计方法[J].电子学报,2014,42 (5):912-917.

MALun,LIAOGui-sheng,etal.Anovelmulti-channelmismatchestimationmethodforparalleltime-interleavedsystem[J].ACTAElectronicaSinica,2014,42 (5):912-917.(inChinese)

[6]XavierBosch-Lluis,IsaacRamos-Perez,etal.Ageneralanalysisoftheimpactofdigitizationinmicrowavecorrelationradiometers[J].Sensors,2011,7(6):6066-6087.

[7]JMWozencraft,IMJacobs.Principlesofcommunicationengineering[M].NewYork:Wiley,1965.205-206.

[8]JRPiepmeier,AJGasiewski,JEAlmodovar,Advancesinmicrowavedigitalradiometry[A].IGARSS2000VolumeVII[C].Honolulu,2000.2830-2833.

陆浩男，1988年生于安徽亳州,中科院博士.研究方向为大规模数字电路,微波辐射计系统研制和定标.

E-mail:luhao0408@126.com

王振占男,研究员1969年生于河北青龙县.研究方向为全极化微波辐射测量技术、定标和应用基础研究;微波辐射计海洋/大气微波辐射传输及参数的反演应用研究等.

Error Analyze of Stokes Parameters Digital Solution

LU Hao,WANG Zhen-zhan,LIU Jing-yi,LI Bin,DONG Shuai

(Key Laboratory of Microwave Remote Sensing,National Space Science Center,Chinese Academy of Sciences,Beijing 100190,China)

Stokesparameteristheintensitydimensiontodescribepolarizedwave.Stokesparameteriswidelyusedinelectromagnetismmeasure,syntheticapertureandradiometer.Thedigitalmethodgiveninthepaperhasthecharactersofhigh-bandwidthandhigh-stability.ThemeasureerrorcontributedbydigitalsamplingforStokesparametersolutionisanalyzedindetailinthepaper.Thebrightnesstemperaturequantizationerrorunderauto-correlationisprovedtobelessthan1*10-5Kinapplicationwith3bitsquantization.Furtherthepapergivesthesystemsensitivity,analyzesthebrightnesstemperatureerrorgeneratedbythedigitalquantization.Whenquantizationisabove3bits,thedigitalsystemsensitivitycanachieve95%ofidealanalogsystem.Thetheoryfoundationofdigitizationsolutionisgiventoproveitsfeasibilityfordifferentdemandindifferentdevice.

Stokesparameter;correlation;digitalsample;quantizationerror

2013-12-04;

2015-08-28；责任编辑：蓝红杰

中国科学院空间科学战略性先导科技专项(No.XDA04061200)

TP274

A

0372-2112 (2016)05-1254-04

电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.035