基于Maxwell关系分析制冷工质磁热效应的研究*

包立夫

(陕西理工学院，陕西　汉中　723001)



基于Maxwell关系分析制冷工质磁热效应的研究*

包立夫

(陕西理工学院，陕西汉中723001)

磁热效应是指对磁性材料进行磁化或退磁时所产生放热或吸热的现象，其本质是材料内部的磁有序度发生改变(熵的改变)，引起材料本身的吸热放热行为。具有磁热效应的磁性制冷工质在制冷工业中有着潜在的应用。等温熵变是衡量磁性制冷工质性能大小的重要参数之一。本文介绍了利用Maxwell关系分析制冷工质性能的原理。针对制冷工质的磁化曲线，阐述了利用Maxwell关系分析具体制冷工质性能的思路和方法，为相关研究人员提供了参考。

Maxwell关系；制冷工质；磁热效应

以气体压缩技术为主的制冷业具有能耗高、污染重的特点，2009年12月的哥本哈根会议明确了各国节能减排的新指标，因此，研发新型低能耗、无污染的制冷技术是当今世界需要迫切解决的问题。磁制冷技术具有绿色环保、高效节能、稳定可靠的特点，近些年来已经引起世界范围的广泛关注。美国、中国、荷兰、日本相继发现的几类高温乃至室温区制冷工质大大推动了人们对普冷温区磁制冷技术的期待[1-4]。这些新型制冷工质的共同特点是磁熵变均高于传统室温磁制冷材料Gd，且相变性质为一级。

磁制冷工质通常具有较大的磁热效应。磁热效应是指磁性制冷工质在被磁化或退磁时，由于内部磁矩的有序度(即熵)发生变化，从而表现出的一种放热或吸热的现象。在零磁场条件下，磁体内磁矩的取向是无序的，此时磁体的熵较大。在外加磁场下，磁体内磁矩沿磁化方向趋于有序排列，熵减小，在等温条件下，磁体向外界放热；当外加磁场减弱或为零时，由于磁性原子或离子的热运动，磁矩又趋于无序，熵增大，磁体在等温条件下从外界吸热。磁热效应是磁性材料的內禀属性。也就是说，任何磁性材料都具有一定的磁热效应。衡量磁热效应的大小，通常用等温熵变(ΔSM)和绝热温变(ΔTad)来表征。

1　Maxwell关系分析磁热效应机理

在热力学中，当系统的约束条件是等温等压时，为了研究的方便，引入了状态函数——吉布斯函数G，其表达式为：

G=U-TS+PV

(1)

对于磁性系统，状态参量还应包含磁化强度M和磁场强度H,于是有：

G=U-TS+PV-MH

(2)

对上式做全微分，有：

dG=dU-TdS-SdT+PdV+VdP-MdH-HdM

(3)

热力学第一定律表明了内能U可以表示成系统状态参量的函数。而熵(S)这一概念也由热力学第二定律引出。综合二者后，我们可以得到热力学基本的微分方程。

dU=TdS-PdV

(4)

式中，T代表温度，P代表压力，S代表熵，V代表体积。对于磁性系统，磁场的功也应该包含在上式之中。所以，磁性系统的内能的微分方程为：

dU=TdS-PdV+HdM

(5)

把磁性系统的内能微分方程(式5)带入吉布斯函数的全微分方程(式3)中可，可以得到：

dG=-SdT+VdP-MdH

(6)

若把吉布斯函数全微分方程写出各个广义力与外参量乘积之和的形式后, 即:

(7)

比较式6和7后，可以得到各个广义力的表达式，这里只关心熵的关系式，即:

(8)

如果吉布斯函数的二阶混合偏导连续(这是麦克斯韦关系式成立的必要前提)，那么对各个广义力表达式取不同外参量的偏导数也应该是连续的。这样，就可以得到麦克斯韦关系式(结合式2和式8)。

(9)

上式成立的依据是交换了对吉布斯自由能的求导次序。所以，吉布斯函数的二阶混合偏导连续是麦克斯韦关系式成立的必要条件。

根据式9，可以得到：

(10)

对于绝热温变，可由热力学第二定律导出。热力学第二定律有：

(11)

(12)

以上就是通过热力学推导出衡量磁热效应的2个参数。

2　Maxwell关系分析磁热效应的应用

在历史上，人们通常使用麦克斯韦关系来研究二级相变的物理量的变化。对于一级相变，则采用克劳修斯-克拉伯龙方程：

(13)

从麦克斯韦关系和克劳修斯-克拉伯龙方程中，可以得出结论。若材料具有较大的磁热效应，应具备：①具有大的dM/dT，即显著的磁化强度的改变。②具有较大的dH/dTc，即磁场对相变温度有较大的驱动率。此外，作为实际应用的磁制冷工质，材料还应具有可调的相变温度，制备工艺简单，成本低廉等特点。

在2004-2006年期间[5]，一些关于MnAs化合物具有“庞磁热效应”的报道陆续发表。这里的庞磁热效应是指材料的磁熵变已经超出理论值。据文献报道称，MnAs在2.23 kbar下的磁熵变可以达到-267 J/kg·K。报道中的解释认为这种庞磁热效应是晶格与磁耦合的结果。不过，后来的研究已经表明，这种庞磁热效应只是一种计算上的假象，是由于采用麦克斯韦关系计算一级相变体系熵变会产生一些假象的峰值[6]。人们对MnAs化合物的庞磁热效应产生的机理进行了分析，然而理论拟合得到的格林爱森常数是很大的负值，这使得人们开始怀疑解释的合理性。实际上，一级相变体系在相变温度附近普遍存在两相共存，这时直接利用Maxwell 关系明显高估了体系的磁热效应，要得到真正的熵变值，需要用比热测量来验证。

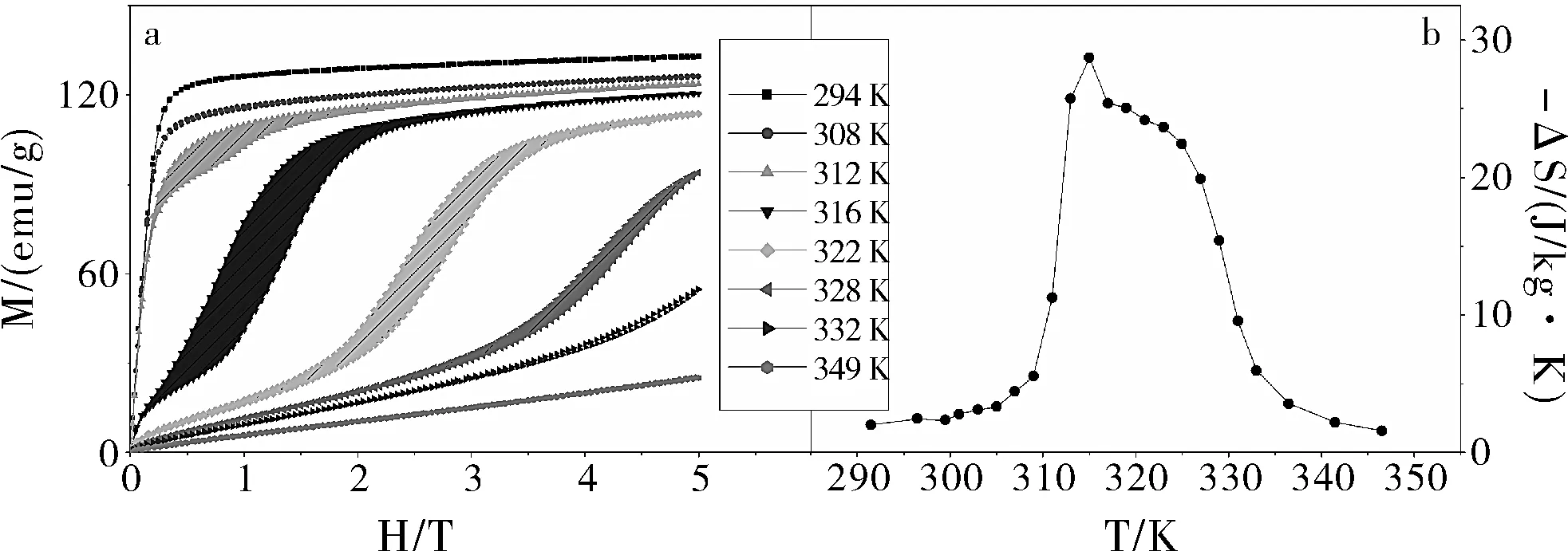
图1　La0.7(Ce,Pr,Nd)0.3Fe11.6Si1.4H1.6在不同温度下的等温磁化曲线(a)和等温熵变随温度的变化(b)

尽管利用麦克斯韦关系计算一级相变材料的熵变一直存在着争议，但是Maxwell关系仍有一定的适用性。一般来讲，n级相变的定义是：在相变点系统的热力学势的第(n-1)阶导数保持连续，而第n阶导数不连续。除了玻色爱因斯坦凝聚是三级相变之外，人们仅观察到了一级、二级相变。而对于计算一级相变磁热效应的主要争议集中在麦克斯韦关系是否可行。从前文已知，麦克斯韦关系成立的条件是体系的吉布斯自由能二阶混合偏导连续。这就是研究者质疑麦克斯韦关系计算一级相变体系熵变的主要原因。当然，在实际的物理体系中，相变几乎不可能在一个温度点上完成，往往是一个过程。研究人员也从数学上推导出麦克斯韦关系其实是与克劳修斯-克拉伯龙方程是一致的。也就是说，用数值积分的方法来近似麦克斯韦关系其实是涵盖了克劳修斯-克拉伯龙方程。所以，通常来讲，对于实际体系采用麦克斯韦关系来计算一级相变材料的磁热效应是合理的。但是，需要注意的是，对于相变区域的熵变尖峰应该扣除。其熵变值应取熵变平台的数值。图1(a)为La0.7(Ce,Pr,Nd)0.3Fe11.6Si1.4H1.6化合物的在不同温度下的磁化曲线，图1(b)为根据麦克斯韦关系来计算样品的等温熵变。这里值得说明的是，ΔS-T曲线中的熵变尖峰值并不是真实的熵变值，这个假象的尖峰是由于采用麦克斯韦关系计算一级相变体系而产生的误差。因而，ΔS-T曲线中熵变平台的最大值为样品真实的熵变值[7]。

3　结　语

由于磁制冷工质的磁热效应和磁性特征直接影响磁制冷的能力和效率，准确的测试对于开发和评估磁制冷材料至关重要。磁热效应通常用等温磁熵变来表征。通过分析制冷工质在不同温度下的磁化曲线，并利用Maxwell关系来计算熵变，这种测试方法简单快捷，因而实验室常常用来测试磁性材料的磁热性能。该方法的优点是测试迅速、可靠性高、可重复性好。考虑到测试精度及计算采用的数值积分所致的误差，熵变的误差范围在3%～10%。但是，在磁性转变温度附近熵变可能引起比较大的误差。对于这种情况，制冷工质的真实熵变不是曲线的尖峰，而是熵变曲线平台中的最大值。

[1]Pecharsky V K, Gschneidner K A. Giant Magnetocaloric Effect in Gd5(Si2Ge2)[J]. Physical Review Letters, 1997, 78(23):4494-4497.

[2]Franco V, Blazquez J S, Ingale B, et al. The Magnetocaloric Effect and Magnetic Refrigeration Near Room Temperature: Materials and Models[J]. Annual Review of Materials Research, 2012, 42(42):305-342.

[3]陈远富,陈云贵,涂铭旌,等. 磁制冷发展现状及趋势[J].低温工程, 2001(1):49-58.

[4]Jr K G, Mudryk Y, Paudyal D. Making the most of the magnetic and lattice entropy changes[J]. Journal of Magnetism & Magnetic Materials, 2009, 321(21):3541-3547.

[5]Ariana D C, Rocco D L, Carvalho A M G, et al. Ambient pressure colossal magnetocaloric effect tuned by composition in Mn1-xFexAs.[J]. Nature Material, 2006, 5(10):802-804.

[6]Amaral J S, Amaral V S. The effect of magnetic irreversibility on estimating the magnetocaloric effect from magnetization measurements[J]. Applied Physics Letters, 2009, 94(4):042506-042506-3.

[7]Bao L F, Hu F X, Chen L, et al. Magnetocaloric properties of La(Fe,Si)13-based material and its hydride prepared by industrial mischmetal[J]. Applied Physics Letters, 2012, 101(16):162406-162406-5.

Study on the Magnetocaloric Effect of Magnetic Refrigerant Based on Maxwell Relations*

BAOLi-fu

(Shaanxi University of Technology, Shaanxi Hanzhong 723000，China)

Magnetocaloric effect (MCE) refers to heating or cooling phenomenon of magnetic materials in the magnetization and demagnetization. The nature of MCE is the changing of magnetic ordering degree (entropy change) in the materials, which can cause heating or cooling behavior of behavior. Magnetic refrigerant with magnetocaloric effect has potential application in refrigeration industry. The isothermal entropy change is one of the important parameters to measure the performance of magnetic refrigerant. The principle of using Maxwell relations was illustrated to analyze the performance of refrigerant. According to the magnetization curve of refrigerant, it was pointed out that method of using Maxwell relations to analyze the performance of specific refrigerant, which provided reference for related researchers.

Maxwell relations; magnetic refrigerant; magnetocaloric effect

包立夫，男，博士，讲师，主要从事磁制冷材料相关领域研究。

TM271

A

1001-9677(2016)010-0009-03

*基金支持：国家自然科学基金青年科学基金项目(NO：11504222)；陕省教育厅专项科研计划项目(NO：15JK1111)；陕西理工学院人才启动项目基金(NO：SLGKYQD2-02)。