能量法分析二元机翼颤振的机理

陆 磊

能量法分析二元机翼颤振的机理

陆 磊

本文研究了基于定常气动力的二元线性气动弹性系统的输入能和耗散能等各种能量之间的关系，以此分析机翼发生颤振的机理。分析表明，机翼发生颤振时，两个自由度间必须存在一定的相位差才能维持系统的周期运动，惯性力对沉浮自由度做的功转换成该自由度的耗散能，惯性力对俯仰自由度做的功转换成该自由度的输入能，系统及子系统的输入能和耗散能均满足相等的关系。系统的颤振频率、两自由度的相位差及振幅比由系统的参数唯一确定。

飞机在飞行过程中受到扰动后将会引起振动，当飞行速度比较小时，由于气动阻尼和系统阻尼的作用，振动会衰减，当速度增大到一定程度后，振动的衰减便逐渐减慢。当达到某一飞行速度后，扰动引起的振幅正好保持不变，这一速度便是颤振临界速度，简称颤振速度。由于颤振是在其本身的运动引起的气动力激励下产生的，所以颤振是一种自激振动。

颤振是一种复杂的物理现象，对于其物理本质，目前国内外几乎所有的气动弹性教材也只是作了简要的定性分析或描述，即使对于线性颤振问题其机理的表述也不甚清楚，非线性颤振是国内外的研究重点，研究的成果非常丰富，但对于产生非线性现象的机理分析却几乎没有。由于对复杂非线性气动弹性现象的机理缺乏完整的理解，在目前的工程界对于非线性气动弹性问题主要解决途径还是尽力降低非线性程度，加大安全系数，利用线性分析手段进行处理。这种方式对较弱的非线性问题是有效的，但这种以提高安全余量保证飞行安全的方法与减轻结构重量提高结构效率的优化设计是背道而驰的。因此，开展线性及非线性气动弹性现象的机理研究显得十分必要。

事实上，颤振作为一种自激振动，属于结构动力响应的范畴，因此，气动弹性系统的稳定性问题可以用自激振动的稳定性理论进行分析。从能量的观点出发，结构振动的稳定性取决于能量的输入与耗散的相互关系。若振幅偏离稳态值时，能量的增减能促使振幅回至稳态值，则平衡状态稳定，反之，平衡状态不稳定。当然，对于气动弹性系统而言，影响系统稳定性的因素并不是系统的振幅，而是来流速度。综上所述，本文从能量的观点首先探讨了基于定常气动力的二元气动弹性系统发生颤振的机理，以便为研究非线性气动弹性现象的机理做铺垫。

模型介绍

图1所示的是一个单位展长的二元机翼的剖面图。机翼的半弦长为b，刚心E距离翼弦中点为ab，a为翼弦中点到刚心的距离占半弦长的百分比，刚心在翼弦中点后时，a＞0。机翼的运动由刚心的浮沉位移h和机翼的绕刚心的俯仰角位移为a（迎风抬头为正）来描述。

二元机翼的运动微分方程为：

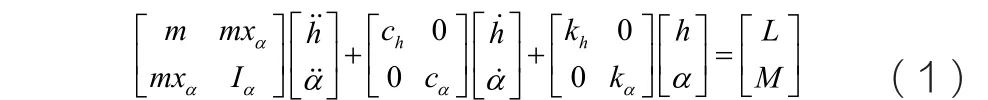
式中，L与M为气动力与气动力矩，为了讨论方便，本文使用定常气动力进行分析，单位展长的二元机翼受到的定常气动力为：

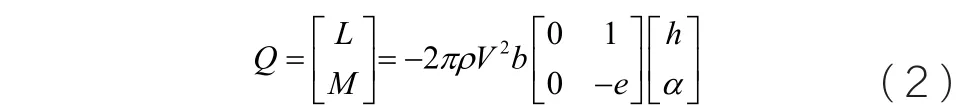
其中， r为空气的密度，V为来流速度，e为气动力中心到刚心的距离，其表达式为e=（0.5+a）b。

为了使用图线形象地展示，这里取一个典型的模型进行分析，模型的几何及物理参数为：

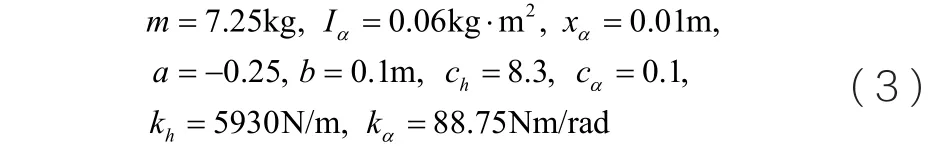
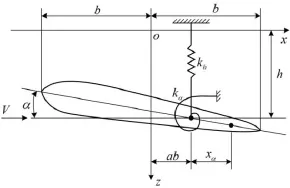
图1　二元机翼的力学模型

该气弹系统的颤振速度VF=23.39m/s。

来流速度等于颤振速度

从颤振的定义与现象可知，当来流速度达到颤振速度时，系统的运动为单频的周期运动，假设系统的运动为：

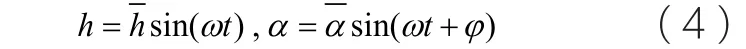
沉浮方向的输入能为：

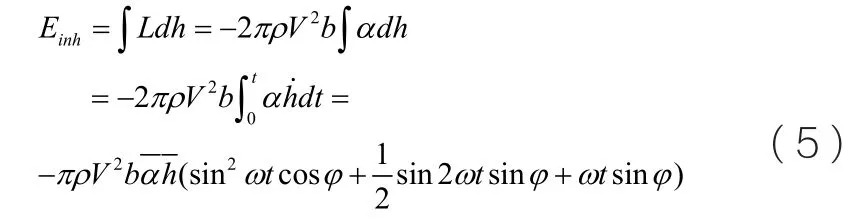
俯仰方向的输入能为：

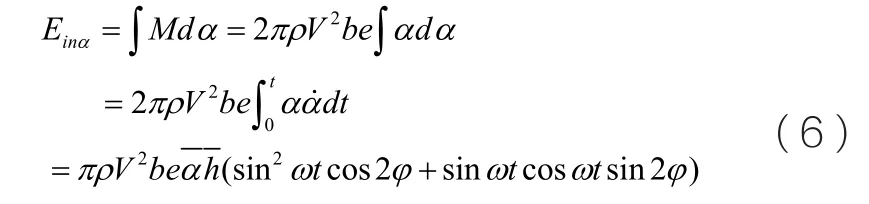
系统的输入能为：

沉浮方向的耗散能为：

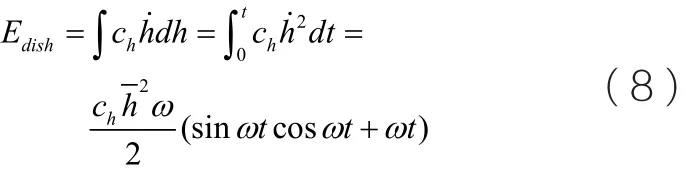
俯仰方向的耗散能为：

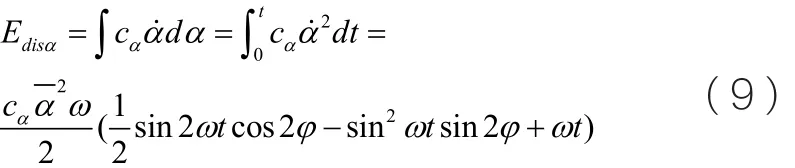
系统的耗散能为：

当分别讨论系统中的沉浮自由度和俯仰自由度的能量时，这里还需介绍惯性力做的功。

惯性力对沉浮自由度做的功为：

惯性力对俯仰自由度做的功为：

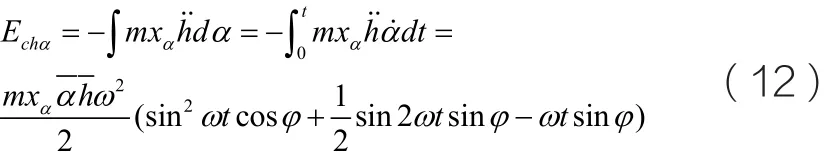
当t=Tz（Tz为运动周期）时，式（5）、式（6）、式（8）、式（9）、式（11）和式（12）的表达式化简为：

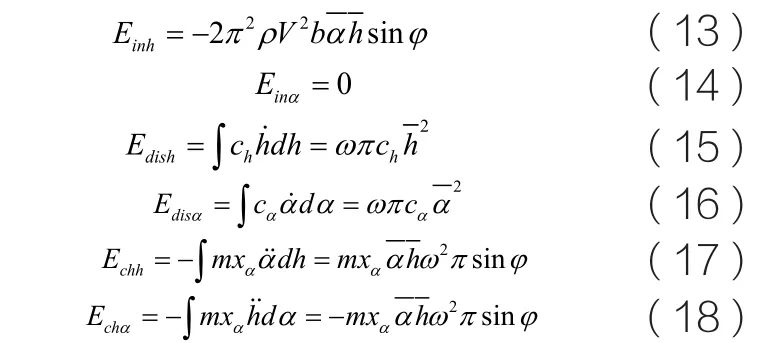
式（14）表明，一周期内，俯仰方向的气动力对系统做功为零，也就是说，该自由度的气动刚度起到了减弱结构刚度的作用。式（17）和式（18）表明一周期内惯性力对沉浮自由度和俯仰自由度做功互为相反数。

颤振作为一种自激振动，从能量的观点出发，自激系统只有系统的输入能和耗散能满足相等的关系才能产生周期运动。由系统输入能等于耗散能可以得到：

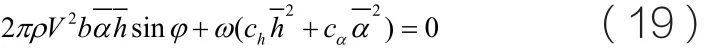
对于系统中的沉浮自由度和俯仰自由度而言，其各自的输入能和耗散能也应该满足相等的关系。以俯仰自由度为例，由于该方向的气动力在一周期内对系统做功为零，因此，该方向的输入能由惯性力对其做的功来提供，即Echa为俯仰方向的输入能，由此得到：

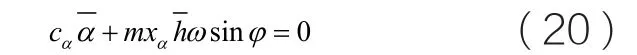
将式（4）代入方程（1）的第一个方程，整理得：

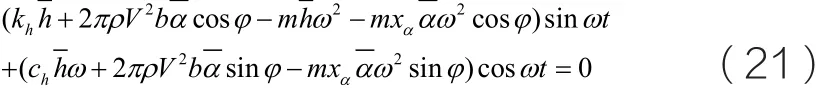
若方程（21）有解，则：

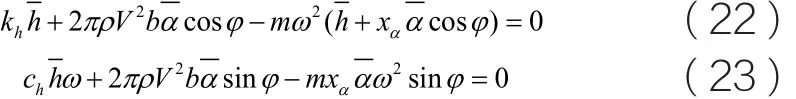
联立求解由式（19）、式（20）、式（22）和式（23）组成的方程组即可得到相应的解。

当V=VF时，上述方程组的解是：

由于方程（1）稳态解的解析表达式较难求得，为了验证上述结论，本文将用数值法求解系统的稳态解。

当V=VF，初始条件为h0=0.1，a0=0.1时（注：为了讨论方便，初始速度均为零），用数值法求得系统的响应，选取稳态周期运动的数据进行函数拟合。选取数据的原则是使浮沉方向的位移从0开始，并将时间更新至从0开始，如图2所示。

拟合的函数形式为：

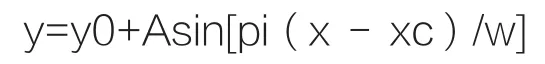
拟合的结果如表1和表2所示。

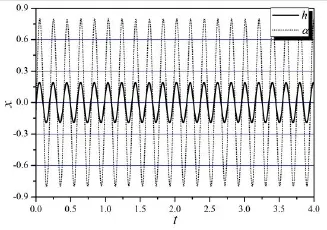
图2　h与a的稳态响应

表1　沉浮方向拟合的结果

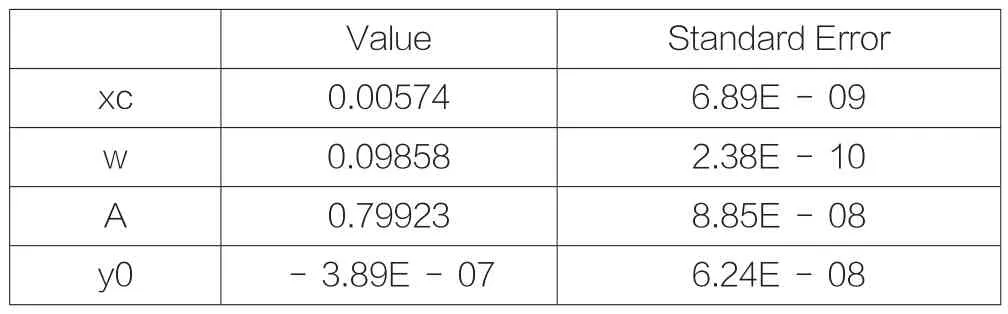
表2　俯仰方向拟合的结果

所以，拟合的沉浮方向与俯仰方向的响应函数分别是：

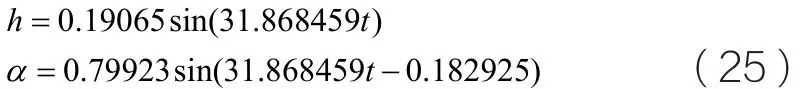
综上所述，当系统发生颤振时，气动力通过沉浮自由度给系统输入能量，由于系统存在惯性耦合，两自由度间的能量转换靠惯性力做功来实现，惯性力对俯仰自由度做的功充当了该自由度的输入能，而惯性力对沉浮自由度做的功充当了该自由度耗散能的一部分，当系统以及子系统各自的输入能和耗散能满足相等的关系时，颤振发生了。

值得指出的是，式（13）和式（14）表明系统的输入能是运动振幅和相位差的函数，式（15）和式（16）表明系统耗散能是运动振幅和振动频率的函数，当系统在颤振速度下作周期运动时，两个自由度间必须维持一定的相位差才能保证系统做的是周期运动。

系统的机械能为：

俯仰自由度的机械能为

系统的机械能、输入能和耗散能随时间的变化如图3所示。图3表明，当二元机翼发生颤振时，系统的机械能周期变化，并且系统的输入能和耗散能在t=nTz/2（n=0，1，2，……）时是相等的，即在半周期内系统的输入能等于系统的耗散能。

另一方面，图3的Esum-Ein+Edis这条曲线是一个常数说明系统的机械能、输入能和耗散能满足如下关系式：

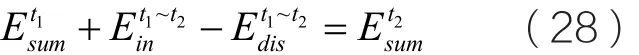
对于俯仰自由度，其机械能、惯性力对其做的功以及耗散能随时间的变化如图4所示。

图4表明，俯仰方向的机械能是周期变化的，在t=nTz/2（n=0，1，2，……）时，惯性力对俯仰自由度做的功和耗散能是相等的，并且Esuma-Echa+Edisa这条曲线是一个常数，这说明俯仰自由度的机械能、输入能和耗散能也满足式（28）的关系。

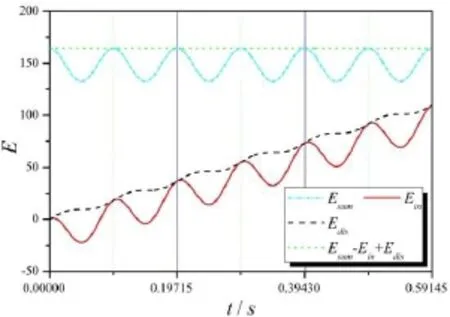
图3　系统的机械能、输入能及耗散能

图4　俯仰方向的能量

来流速度不等于颤振速度

若来流速度小于颤振速度，响应是收敛的；若来流速度大于颤振速度，则响应是发散的，也就是说，当来流速度不等于颤振速度时，系统的响应函数包含指数成分，在这种情况下，系统的解的解析表达式较难求得，这也造成了与解有关的一些计算难以进行，如能量的计算。然而，用数值法对运动方程进行直接求解则可以克服这些弊端。下面本文将用数值法来计算当来流速度不等于颤振速度时系统的各种能量，进一步探讨二元机翼发生颤振的原因。

也许你此时正觉得自己一无是处，为自己对什么都不感兴趣而不知所措，甚至烦闷不已。你要明白，也许你并不是对什么都不感兴趣，只是没有去接触而已。

系统的输入能为：

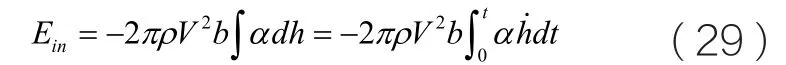
系统的耗散能为：

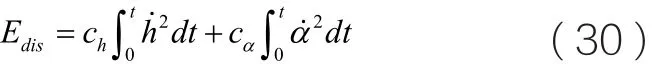
图5　V=20.0时系统的响应

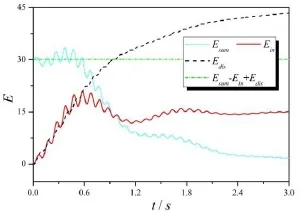
图6　V＜VF时系统的能量

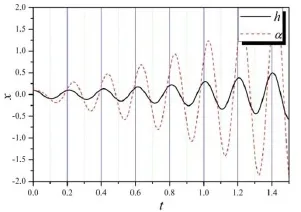
图7　V=25.0时系统的响应

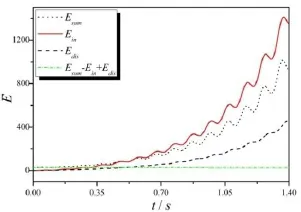
图8　V＞VF时系统的能量

来流速度小于颤振速度

当V=20.0，初始条件为h0=0.1，a0=0.1时，用数值法求得系统的响应，如图5所示。

通过对图5的响应曲线进行傅里叶分析，结果表明，沉浮方向是单频振动，而俯仰方向是多频振动，该方向的频率除了自身的固有频率外，还包含了沉浮方向的振动频率。

系统的机械能、输入能和耗散能随时间的变化如图6所示，图6说明当系统的来流速度低于颤振速度时，系统的输入能小于耗散能，以致系统的机械能不断减少，最后系统的响应收敛至平衡位置。另一方面，系统的机械能、输入能和耗散能满足式（28）的关系。

来流速度大于颤振速度

当V=25.0，初始条件为h0=0.1，a0=0.1时，用数值法求得系统的响应，如图7所示。通过对图7的响应曲线进行傅里叶分析，结果表明，沉浮方向和俯仰方向是同一频率的单频振动。

系统的机械能、输入能和耗散能随时间的变化如图8所示，分析表明当系统的来流速度大于颤振速度时，系统的输入能大于耗散能，以致系统的机械能不断增加，从而使系统的响应发散。Esum-Ein+Edis这条曲线是一个常数体现了系统得机械能、输入能和耗散能也满足式（28）的关系。

结语

本文从能量的观点分析了二元机翼不同时刻的机械能以及不同时间区间系统的输入能、耗散能，以探讨二元机翼发生颤振的机理，得到的结论如下。

1）当系统的输入能等于耗散能时，系统发生颤振；当输入能小于耗散能时，系统的响应收敛至平衡位置；当输入能大于耗散能时，系统的响应发散。

2）当系统在颤振速度下作周期运动时，两个自由度间必须存在一定的相位差才能维持系统的周期运动。当一个系统的系统参数确定了之后，该系统的颤振频率、两自由度的相位差及振幅比也就确定了。

3）俯仰方向的输入能靠惯性力对其做的功提供，惯性力对沉浮自由度做的功转换成了该自由度耗散能的一部分，系统发生颤振时，对于系统及子系统而言，其输入能和耗散能同样满足相等的关系。

陆 磊

上海飞机设计研究院

陆磊，男，硕士，上海飞机设计研究院。

DOI：10.3969/j.issn.1001-8972.2016.08.010