基于随机扩散理论的色谱动力学模拟

孙寅璐，郭　彦，赵健伟

(1. 南京大学 化学化工学院 生命分析化学国家重点实验室，南京 210008；2. 南京信息工程大学 环境科学与工程学院 江苏省大气环境监测与污染控制高技术研究重点实验室，南京 210044)



基于随机扩散理论的色谱动力学模拟

孙寅璐1，郭彦2，赵健伟1

(1. 南京大学 化学化工学院 生命分析化学国家重点实验室，南京 210008；2. 南京信息工程大学 环境科学与工程学院 江苏省大气环境监测与污染控制高技术研究重点实验室，南京 210044)

为了深入理解粒子扩散对色谱过程动力学的影响，利用微尺度受限空间内随机行走的方法对待分离粒子在气相色谱填充柱内的扩散过程进行了动态模拟.重点考察了固定相的填充率和排布方式、柱压和柱长对色谱动力学的影响.结果表明，短柱和大填充率有利于提高柱效，而固定相的排布方式对柱效影响较小.待分离粒子的运动表现出微尺度空间限域的超扩散运动特征，其轴向扩散行为随着柱内压力的增加而愈发明显.本文提出的模拟方法对加速优化分离过程和开发新型色谱分离技术具有参考意义.

随机行走； 色谱动力学； 粒子扩散； 固定相

粒子扩散问题是微观理论化学研究中的基本问题，在微流控、微通道、微反应器等领域中引起了研究者们的广泛关注.粒子扩散与输运行为密切相关，是研究传质过程和计算传质速率的重要基础.实验上通常采用荧光显微镜、原子力显微镜等单粒子跟踪技术来追踪粒子的扩散过程[1].这些技术手段大大提高了人们对粒子微观运动的认识，然而基于现有的技术水平，依靠实验方法还不足以获得较为全面的扩散信息.随着计算技术的飞速发展，计算机模拟方法将成为分子微观行为研究中的重要辅助手段.它打破了实验技术水平的限制，同时各实验条件参数经过计算机模型化处理后更能清晰准确的表达对扩散行为的影响，从而揭示出粒子扩散的本质规律以及不同操作条件下的扩散模式，为实验提供理论基础.

色谱法是分离分析中最为常见的方法之一，其分离过程中的扩散问题是色谱动力学研究的基础.深入理解粒子在两相中的扩散和传质行为，探索不同条件下的扩散机理，可有效控制峰展宽、提高分离度，为实现快速优化分离、提升色谱性能和改进分离器件提供了重要的理论依据.

以色谱过程热力学为基础的分离理论和以扩散过程为基础的峰形预测理论，均能很好的阐述色谱的保留值规律和峰形规律.但是这些理论属于宏观理论，没有考虑到分离器件内填充物的形状、大小、填充密度和表面理化性质对分离分析的影响，然而这些微观性质对分离效果至关重要.因此色谱理论的发展亟需从微观角度对色谱的分离规律、条件控制开展模拟研究.Slusher等[2]用分子动力学方法计算了反相色谱体系中，溶剂密度和取向分布与色谱柱壁之间距离的函数关系.Sun等采用分子动力学方法分别模拟了配体密度[3]和溶剂pH[4]对蛋白质在疏水电荷诱导色谱中的吸附脱附行为的影响.Makrodimitris等[5]应用格子-偶极模型在介观尺度上模拟了肽链在反相色谱上的吸附行为.Turowski等[6]应用MM+力场和AM1半经验方法计算了脂肪族和芳香族溶质的范德华半径、与固定相和流动相的相互作用，及这些作用情况在反相色谱分离中的应用.Sarti等[7]应用数学模型研究了蛋白质在膜亲和相色谱中的吸附平衡和流出曲线.Siepmann课题组长期致力于色谱的蒙特卡罗模拟研究，例如考察气相色谱中气液界面的吸附和分配[8]，非极性和极性物质在反相液相色谱中的保留机理[9]，待测物质在气相色谱中的过保留行为[10]以及流动相改性对分配的影响[11]等等.

总体而言，以上描述微观扩散的方法可分为分子动力学和蒙特卡罗两种.分子动力学方法[12-15]是一种确定性的模拟方法，其优势在于可全面模拟体系所经历的物理化学全过程，精确获取体系内部各种物理化学信息.而蒙特卡罗方法[16-18]是随机动力学方法，求解问题通过建立概率模型然后统计分析得出，该方法侧重于结果而忽略过程中的细节.目前这两种方法均用于处理色谱吸附热力学、待分离物质的性质以及溶剂化环境等局部问题，尚未用于研究色谱扩散分离的整体情况，实现色谱的全过程模拟.这是因为现有的计算水平往往适用于较小的扩散体系，而对于色谱分离等较大规模的扩散体系来说，计算量过大，模拟用时远远超过可以接受的程度.

为了既能保留扩散分离过程中的重要细节，同时又能兼顾全过程模拟，我们结合分子动力学和随机运动理论[19-23]的优势提出了一种新的简化方法——受限空间内的随机行走模拟方法.该方法保留了制约扩散行为的关键信息，对粒子间的相互作用进行合理简化，将模拟步长的时间尺度放大，从而减小运算量，提高运算效率，使大体系扩散过程模拟成为可能.该方法可模拟分离过程中的粒子运动、碰撞、分离介质的性质等微观细节，其模拟结果更为准确可靠，同时也可促进分离条件的优化和分离器件的改进.由于模拟的规模足够大、时间足够长，其结果可与一般宏观测量信号相对照，也可与基于宏观理论的模拟作对比.该方法在大规模体系、长时间分离过程的模拟中找到了计算量与计算体系之间的平衡点，现已应用于膜渗透过程[24-25]和电化学过程[26-27]的粒子扩散行为的模拟研究中.

本文根据粒子在色谱中的基本运动规律，设计了粒子在含有周期排布势垒的二维受限空间内随机行走的仿真模型，模拟粒子在填充柱中的扩散行为.重点考察了势垒的填充率和排布方式、柱压和柱长对色谱动力学的影响.

1　模型与方法

如图1所示，将填充柱定义为二维平面空间，该空间在x方向上无限延伸，y方向上有上下两个边界.空间内包含周期排布的结构单元，如虚线框所示.结构单元内均包含一圆形势垒用于模拟固定相.粒子不可进入势垒，只能在势垒以外的区域内运动.虚线方格表示的结构单元中，空白部分代表粒子可自由运动的区域，红色曲线代表粒子的运动轨迹.组分在色谱柱内的总体运动趋势是沿着柱长的方向迁移(近似一维分离体系)，所以我们主要研究粒子在x方向上的扩散行为.

采用忽略了质量和体积的质点来表示待分离粒子.粒子的速度由两部分组成，一是粒子自身扩散的随机速度δ，其大小与粒子的相对分子质量和温度相关，其方向随机产生，即以粒子为中心360°范围内等概率分布；另一速度为在x轴向上给粒子施加的附加速度uM，用于模拟载气定向流动时对粒子的推动作用.需要注意的是，模型中的随机速度并非仅为粒子在真空中的热运动速度，它实际上是一种表观速率，是对粒子自身的热运动、粒子与其他粒子的碰撞、粒子与势垒的碰撞以及粒子与载气分子的碰撞等各种因素相互作用后的综合体现.

粒子和势垒之间的相互作用可用多种模型来描述，本章采用弹性碰撞模型[28]来简化处理.假定粒子在某一小段时间内随机速度保持不变，那么随机速度和时间步长的乘积决定了行走一步的步长.在不受势垒阻碍下，根据粒子的当前位置和每步步长即可确定粒子完成一步之后的位置.当粒子与势垒碰撞时，其扩散速度大小不变，方向上遵从反射定律，即粒子以原方向的反射方向继续在色谱柱中运动.对粒子的步点位置进行时间积分获得运动轨迹，根据运动轨迹来分析粒子的扩散行为及分离效果.

2　结果与讨论

应用上述模型研究了待分离粒子在填充柱内的扩散行为，重点考察了势垒的填充率和排布方式、柱压和柱长等因素对色谱动力学行为的影响.模拟温度均为298K，根据气体布朗运动理论估算可将粒子的随机速度设为20mm·s-1，时间步长设为0.005s·step-1.若无特殊说明，势垒粒径为 0.6mm，载气流速为2mm·s-1，模拟时间为500s(对应长度为1m的填充柱).当体系浓度较低时，粒子之间的运动是相互独立的，可将多粒子的随机运动视为单粒子的多次随机运动.实验中的检测信号为粒子在色谱柱内保留时间的统计分布；同样地，粒子在给定时间内运动的位移也存在统计分布，即浓度分布.应用已建立的单粒子随机行走模型对每个模拟条件均实施1000次模拟，以浓度分布的统计均值作为分析结果.

2.1填充率

固定相填充质量的优劣直接影响到色谱柱的柱效.在模拟中，我们用势垒的填充率大小来反映色谱柱固定相的填充情况.填充率用势垒面积和单元格面积的比值表示.在周期单元格大小不变的条件下，势垒粒径小，则填充率小，相当于固定相填充得较为疏松的色谱柱；反之，势垒粒径大，则填充率大，相当于固定相填充得较为紧实的情况.模拟中，势垒粒径大小分别设置为0.98，0.90，0.80，0.60和0.20mm，相对应的填充率分别为75%，63%，50%，28%和3%.

图2为同一载气流速下，随势垒粒径的变化，粒子沿x轴向扩散的统计分布图.图中曲线为高斯拟合得到的色谱峰.当势垒粒径从0.20mm增大到0.98mm时，相当于固定相填料粒度由大变小，色谱峰在x轴向上的浓度分布的平均位移变小，峰形逐渐变得窄而尖，柱效提高.

色谱中的涡流扩散过程与填充技术、固定相颗粒大小以及颗粒均匀度密切相关.色谱柱参数中，固定相的填充情况可以用涡流扩散项A来描述：

A=2λdp；

(1)

均方位移(Mean Square Displacement， MSD)[29-32]为粒子位移平方的平均值，用来表征粒子在体系中的平均扩散距离.它反映了粒子的扩散速率，是时间(或步数)t的函数，由下式给出：

(2)

其中N是总步数，dk表示粒子在k步后的位置矢量(d0是初始位置)，|dk+t-dk|表示k步到k+t步的位移矢量.

MSDx和MSDy分别为MSD在x和y方向上的分量，定义为

(3)

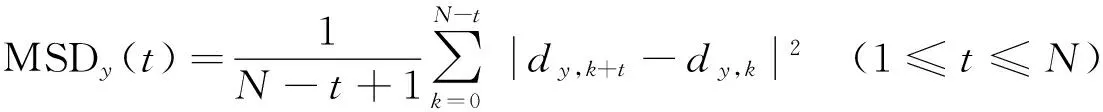
(4)

其中dx，k和dy，k分别为dk的x和y方向上的分量.

MSD的意义在于可以通过求解MSD得到粒子的扩散系数D.在二维空间内，MSD和D有如下关系[33]：

MSD=4Dtα，

(5)

指数α反映了粒子的运动模式：当α=1时，代表布朗运动，即自由扩散；当α=2时，代表理想的定向运动；当1<α<2时，介于布朗运动和定向运动之间，这种有方向的扩散被称为超扩散运动；当0<α<1时，表现为受限区域内的扩散过程，被称为次扩散运动.

图3为粒子在不同势垒粒径下的MSD变化图.从总体上看，MSD随势垒粒径的减小而增大，表明粒子在势垒粒径较小时扩散能力较强，这与先前研究的模拟结果一致[34].由于x方向施加了定向速度，所以粒子的MSDx和MSD曲线类似，均随时间呈指数增加.由于粒子在y方向上表现为自由扩散，MSDy随时间线性增加，所以在相同的扩散时间内MSDx要远高于MSDy.模拟中，粒子既存在受限空间内的次扩散运动，同时又受到载气驱动的影响而具有超扩散运动特征.为了进一步揭示其内在扩散机制，我们对MSD曲线进行拟合，得到各粒径对应的D和α，结果见表1：

表1　不同势垒粒径下拟合MSD得到的D和α参数

由表1可知，α值介于1和2之间表明了粒子在该条件下的超扩散运动行为.虽然势垒会在一定程度上阻碍粒子的扩散运动，但其影响非常微弱，从α值均接近于2可以看出，载气的推动作用仍占主导地位，粒子的整体扩散行为更接近于定向运动.随势垒粒径的减小，粒子受到势垒的阻碍作用越小，其自由扩散和定向扩散的空间越大，扩散能力显著提高，同时其定向运动趋势也愈发明显.

平均位移(Average Displacement， AD)反映粒子平均一步的位移.计算采用逐差法，以步数的一半为分界把位点分为前后两组，计算后一组第一个点和前一组第一个点之间的位移，以此类推，算出所有位移后取平均，再除以两点之间的步数差，求出平均一步的位移.分别计算x和y分量，把两分量相加即为实际的位移矢量.

对某一运动轨迹，若总步数N是奇数，则位点数目N+1是偶数，令N+1=2n，则有

(6)

若总步数N是偶数，则位点数目N+1是奇数，令N+1=2n+1，则有

(7)

最后

AD=ADx+ADy

(8)

图4为不同势垒粒径下对应的平均位移.从(a)中明显看出粒子在x方向上的位移随势垒粒径的增大而减小，其中500s处各粒径对应的平均位移与图2中的各峰值点对应一致.而粒子在y方向表现为自由扩散，故其扩散位移随粒径没有明显的变化规律，如图(b)所示.

2.2势垒排布

除势垒粒径外，势垒的排布方式也可能影响粒子的扩散行为.我们假定势垒大小不变，通过改变晶胞角度来改变势垒排布，适当调整晶胞尺寸大小以消除填充率的改变而造成的结果差异.本部分共设计了四种势垒排布方式，晶胞角度从90°开始依次减小15°直至45°.不难发现，当晶胞角度为45°时势垒的排布方式与90°的情况相同，如图5所示.

由晶胞角度引起的MSD、MSDx、MSDy和ADx的差异相比势垒粒径要小得多，但仍表现出一定的变化规律.随晶胞角度变小MSD、MSDx、MSDy(图6，见第194页)和ADx(图7(a)，见第194页)均呈现出先上升(90°减小到60°)后下降(60°减小到45°)的趋势，这与y方向上势垒之间的距离变化规律一致；而ADy没有明显的变化规律(图7(b)).

表2　不同晶胞角度下拟合MSD得到的D和α参数

对MSD进行拟合，得到各晶胞角度对应的D和α，结果见表2.通过改变晶胞角度实现了对粒子扩散空间的调整，扩散空间的相对扩大有利于提高粒子的次扩散能力，表现为D和α都略有增加.然而对于色谱中以超扩散运动为主的粒子来说，这种影响是非常微弱的.

2.3柱压

气相色谱柱压是通过调节载气流速实现的，流速越大柱压越大.在模拟中，我们通过改变驱动速度的大小来描述压力的变化情况.设势垒粒径为0.6mm，载气流速在x轴向的线速度分别设定为1，2，4mm·s-1，考察了500s内载气流速的变化对粒子扩散分离的影响.

表3　不同流速下拟合MSD得到的D和α参数

如图8所示，在相同扩散时间内MSD和MSDx随载气流速增加而显著增加，这与图3随粒径减小时的情况相似.实际上，减小势垒粒径相当于间接提高了载气的推动作用，二者对粒子在x轴向扩散的影响在本质上是一样的.而MSDy随载气流速增加略有下降，表明x方向加载较大的载气流速会对y方向的自由扩散产成轻微的削弱影响.

对MSD曲线进行拟合，得到各流速下对应的D和α，见表3.结果表明，载气流速越大粒子的流动性越明显，其扩散能力显著增强，D近乎呈指数增长.所以在保证一定分离度的前提下，适当增加载气流速可有效缩短待测物质的保留时间，进而提高分离效率.

2.4柱长

我们进一步考察了柱长对粒子分离扩散的影响.通过增加随机步数、延长粒子在柱内的扩散时间来表达柱长增加.以势垒粒径为0.6mm为例，步数分别设置为1.0×105，2.0×105，3.0×105，5.0×105和8.0×105步，即分离时间分别为500，1000，1500，2500，4000s，对应模拟长度分别为1，2，3，5，8m的色谱柱.

图9为不同柱长沿x轴向扩散的位移统计分布图.结果表明，柱子越长，粒子的浓度分布越宽.影响色谱峰宽的因素包括涡流扩散、纵向分子扩散和传质阻力.由于简化了粒子与固定相的相互作用，峰展宽主要受分子纵向扩散的影响.柱长越长，粒子的纵向扩散时间越长，峰展宽越严重，柱效显著下降，所以在实际经验中在确保待分离物质完全分离的前提下都尽可能使用短柱.

(9)

对随机速度进行累加，得到位移的方差σdis为

(10)

式(10)表明峰宽与粒子扩散步数的平方根成正比.由于步数和柱长相对应，因此峰宽与柱长的平方根成正比.插图亦表明了半峰宽(FWHM)与柱长平方根的线性关系，证实了我们的模拟结果与理论推导的一致性.

利用随机行走算法对气相色谱中粒子在填充柱中的扩散过程进行了动态模拟，流出曲线呈高斯分布.运用MSD和AD方法对粒子的扩散运动轨迹进行分析，从总体上看，待分离粒子表现出微尺度空间限域的超扩散运动特征.通过拟合MSD方程求解扩散系数的方法，直观地比较了势垒的粒径大小、柱压和柱长对粒子扩散能力的影响程度，模拟结果表明增大填充率、增加柱压和减小柱长都会提高柱效，而势垒的排布方式对色谱动力学的影响不明显.

[1]CLARIDGE S A， SCHWARTZ J J， WEISS P S. Electrons， photons， and force：quantitative single-molecule measurements from physics to biology [J].ACSNano， 2011，5(2)：693-729.

[2]SLUSHER J T， MOUNTAIN R D. A molecular dynamics study of a reversed-phase liquid chromatography model [J].JPhysChemB， 1999，103(8)：1354-1362.

[3]ZHANG L， ZHAO G， SUN Y. Effects of ligand density on hydrophobic charge induction chromatography：Molecular dynamics simulation [J].JPhysChemB， 2010，114(6)：2203-2211.

[4]ZHANG L， ZHAO G， SUN Y. Molecular dynamics simulation and experimental validation of the effect of pH on protein desorption in hydrophobic charge induction chromatography [J].MolSimulat， 2010，36(13)：1096-1103.

[5]MAKRODIMITRIS K， FERNANDEZ E J， WOOLF T B，etal. Mesoscopic simulation of adsorption of peptides in a hydrophobic chromatography system [J].AnalChem， 2005，77(5)：1243-1252.

[6]TUROWSKI M， YAMAKAWA N， MELLER J，etal. Deuterium isotope effects on hydrophobic interactions：the importance of dispersion interactions in the hydrophobic phase [J].JAmChemSoc， 2003，125(45)：13836-13849.

[7]DIMARTINO S， BOI C， SARTI G C. A validated model for the simulation of protein purification through affinity membrane chromatography [J].JChromatogrA， 2011，1218(13)：1677-1690.

[8]WICK C D， SIEPMANN J I， SCHURE M R. Molecular simulation of concurrent gas-liquid interfacial adsorption and partitioning in gas-liquid chromatography [J].AnalChem， 2002，74(14)：3518-3524.

[9]RAFFERTY J L， ZHANG L， SIEPMANN J I，etal. Retention mechanism in reversed-phase liquid chromatography：A molecular perspective [J].AnalChem， 2007，79(17)：6551-6558.

[10]WICK C D， SIEPMANN J I， SCHURE M R. Influence of analyte overloading on retention in gas-liquid chromatography：A molecular simulation view [J].AnalChem， 2002，74(1)：37-44.

[11]WICK C D， SIEPMANN J I， SCHURE M R. Simulation studies on the effects of mobile-phase modification on partitioning in liquid chromatography [J].AnalChem， 2004，76(10)：2886-2892.

[12]KESKIN S. Adsorption， diffusion， and separation of CH4/H2mixtures in covalent organic frameworks：molecular simulations and theoretical predictions [J].JPhysChemC， 2012，116(2)：1772-1779.

[13]KESKIN S. Atomistic simulations for adsorption， diffusion， and separation of gas mixtures in zeolite imidazolate frameworks [J].JPhysChemC， 2011，115(3)：800-807.

[14]GURDAL Y， KESKIN S. Atomically detailed modeling of metal organic frameworks for adsorption， diffusion， and separation of noble gas mixtures [J].IndEngChemRes， 2012，51(21)：7373-7382.

[15]LI J R， KUPPLER R J， ZHOU H C. Selective gas adsorption and separation in metal-organic frameworks [J].ChemSocRev， 2009，38(5)：1477-1504.

[16]TOBITA H， HAMASHIMA N. Monte Carlo simulation of size exclusion chromatography for randomly branched and crosslinked polymers [J].JPolymSciPolymPhys， 2000，38(15)：2009-2018.

[17]WERNEKENSCHNIEDER M， ZINN P. Monte-Carlo simulation of gas chromatographic separation for the prediction times and peak half widths [J].Chromatographia， 1989，28(5-6)：241-248.

[18]DONDI F， MUNARI P， REMELLI M，etal. Monte Carlo model of nonlinear chromatography [J].AnalChem， 2000，72(18)：4353-4362.

[19]AVRAMOV I， ARGYRAKIS P. Particle separation using high frequency alternating external fields [J].Langmuir， 2002，18(8)：3376-3379.

[20]GIDDINGS J C， EYRING H. A molecular dynamic theory of chromatography [J].JPhysChem， 1955，59(5)：416-421.

[21]FELINGER A， PASTI L， DONDI F，etal. Stochastic theory of size exclusion chromatography：Peak shape analysis on single columns [J].AnalChem， 2005，77(10)：3138-3148.

[22]FELINGER A. Determination of rate constants for heterogeneous mass transfer kinetics in liquid chromatography [J].JChromatogrA， 2006，1126(1/2)：120-128.

[23]PASTI L， CAVAZZINI A， FELINGER A，etal. Single-molecule observation and chromatography unified by levy process representation [J].AnalChem， 2005，77(8)：2524-253

[24]FU Y Q， CHEN L L， SUN W，etal. Simulation for diffusion behaviour of molecules in nanopattern-supported lipid bilayers based on random walk theory [J].MolSimulat， 2014，40(4)：313-319.

[25]FU Y Q， CHEN L L， KE J Y，etal. Simulate the diffusion of hydrated ions by nanofiltration membrane process with random walk [J].MolSimulat， 2012，38(6)：491-497.

[26]KE J Y， FU Y Q， CHEN L L，etal. The random walk simulation of the ions diffusion in the membrane materials of lithium-ion battery [J].JFudanUniversity(NatureScience)， 2012，51(2)：251-254.

[27]ZHAO J W， CHEN L L， FU Y Q，etal. A new random walk simulation model for study of diffusion behavior of single particle within two-dimentional space [J].JElectrochem， 2012，18(5)：427-436.

[28]JIN S， VERKMAN A S. Single particle tracking of complex diffusion in membranes：Simulation and detection of barrier， raft， and interaction phenomena [J].JPhysChemB， 2007，111(14)：3625-3632.

[29]BALDUCCI A， MAO P， HAN J，etal. Double-stranded DNA diffusion in slitlike nanochannels [J].Macromolecules， 2006，39(18)：6273-6281.

[30]HOFLING F， FRANOSCH T， FREY E. Localization transition of the three-dimensional Lorentz model and continuum percolation [J].PhysRevLett， 2006，96(16)：165901.

[31]MICHALET X. Mean square displacement analysis of single-particle trajectories with localization error：Brownian motion in an isotropic medium [J].PhysRevE， 2010，82(4)：041914.

[32]KENKRE V M， GIUGGIOLI L， KALAY Z. Molecular motion in cell membranes：Analytic study of fence-hindered random walks [J].PhysRevE， 2008，77(5)：051907.

[33]SAXTON M J. Single-particle tracking：Effects of corrals [J].BiophysJ， 1995，69(2)：389-398.

[34]GUO Y， FU Y Q， SUN Y L，etal. Theoretical simulation on the chromatographic system based on the random diffusion of the separating particles [J].ActaPhys-ChimSin， 2012，28(12)：2797-2802.

[35]NIEHAUS A M S， VLACHOS D G， EDWARDS J S，etal. Microscopic simulation of membrane molecule diffusion on corralled membrane surfaces [J].BiophysJ， 2008，94(5)：1551-1564.

[36]ROSENBLATT M. A central limit theorem and a strong mixing condition [J].ProcNatlAcadSciUSA， 1956，42(1)：43-47.

Simulation of Chromatographic Dynamics Based on Random Diffusion

SUN Yinlu1， GUO Yan2， ZHAO Jianwei1

(1. State Key Laboratory of Analytical Chemistry for Life Science， School of Chemistry and ChemicalEngineering，NanjingUniversity，Nanjing210008，China； 2.KeyLaboratoryofAtmosphericEnvironmentMonitoringandPollutionControlofJiangsuProvince，SchoolofEnvironmentalScienceandEngineering，NanjingUniversityofInformationScienceandTechnology，Nanjing210044，China)

In order to thoroughly understand the influence of particle diffusion on chromatographic dynamics， we developed a model based on the theory of random walk in confined space and apply it to dynamical simulation of particle diffusion in a GC packing column. The effects of packing fraction and barrier arrangement of the stationary phase as well as pressure and column length on the chromatographic dynamics have been investigated in detail. It was demonstrated that short column and large packing fraction contributes to high column efficiency， while barrier arrangement of the stationary phase only has a slight effect on column efficiency. The super-diffusion of particles is characterized in confined space and the axial diffusion rises with the increasing pressure. The simulation method has some significance for the acceleration of optimization processes and the development of novel technologies of chromatographic separation.

random walk; chromatographic dynamics; particle diffusion; stationary phase

0427-7104(2016)02-0189-10

2015-07-14

国家自然科学基金(21121091，21273113)

孙寅璐(1990—)，女，硕士研究生；赵健伟，男，教授，博士生导师，通讯联系人，E-mail：zhaojw@nju.edu.cn.

O 657

A