智能算法用于汽油馏程蒸发温度的计算

张柳莺, 任莹莹

(中国石油化工股份有限公司广东石油分公司，广东　广州　510000)



智能算法用于汽油馏程蒸发温度的计算

张柳莺, 任莹莹

(中国石油化工股份有限公司广东石油分公司，广东广州510000)

探讨了人工神经网络法和径向基神经网络法，用于GB/T6536《石油产品蒸馏测定法》测定汽油馏程试验时，从馏出温度计算蒸发温度的可能性。试验表明，线性神经网络法的泛化预测能力，优于径向基神经网络法。用所选的训练集数据建立数学模型后，测试集数据的仿真结果表明，仿真值与原测定值的绝对偏差，没有超过2 ℃，说明线性神经网络法用于汽油蒸发温度的计算是可行的，该方法是一种快速、准确、简便值得借鉴的方法。

汽油馏程；蒸发温度换算；线性神经网络法；MATLAB

车用汽油规格指标中，要求用蒸发温度表述其蒸发性能的优劣。通常汽油的蒸发温度是采用GB/T6536-2010《石油产品蒸馏测定法》测定的。实验中，使用测得的馏出温度，通过换算，得到所需的各点蒸发温度，过程较为繁琐，给使用者带来不便[1]。目前使用计算机的智能算法在众多学科研究和工程应用中已得到广泛应用，取得不少可喜的成果[2-4]。笔者尝试在汽油馏程测定中，使用线性神经网络(Linear Neural Networks，LNN)法完成各点馏出温度到蒸发温度的计算。试验表明，LNN法用于汽油馏程蒸发温度计算是可行的，该方法具有快速、简便、准确的特点，是一种值得借鉴的方法。

1　实　验

1.1仪器设备与试样

德国海尔潮 PAC OPTIDIST型自动馏程测定仪；大气压力计。

油品93#、97#车用汽油。

1.2实验过程

按照GB/T6536《石油产品蒸馏测定法》来测定其馏程，记录初馏点(initial boling point, ibp)、5%、10%、20%、30%、40%、50%、80%、90%、95%和终馏点(final boling point, fbp)的馏出温度，记录测试现场的大气压，并按照规程的要求，求出蒸发损失量等数据，最后按照规程指定的方法，计算出要求的各点蒸发温度[1]。

用LNN法计算各点的蒸发温度时，是将训练集的ibp、10%、50%、90%、fbp的馏出温度、蒸发损失量和测定时的大气压数据，作为输入向量，将上述各点对应的蒸发温度作为目标向量，输入到预先安装了MATLAB软件的计算机中，用其中的神经网络工具箱中的LNN网络函数，建立数学模型，然后用测试集数据考察模型的“泛化”预测能力，模型泛化能力满意时，就可以在实际测定时，用来仿真预测上述各点的蒸发温度。

2　结果与讨论

2.1智能算法的优越性及方法的选择

智能算法是一种高效的信息处理技术，解决了众多学科研究和工程应用中许多重要问题。它是从已知的数据出发，运用当今新技术、新理论，如支持向量机、神经网络、决策树、粗糙集理论、模糊集理论和智能仿生计算等，提取其中的特征量，然后再进行特征抽取以确定合适的特征量，张成模式空间或特征空间，最后通过智能算法进行训练和判别，来揭示已知数据信息中隐含的性质和规律，为人们提供有用的决策依据和过程优化的重要信息[2-3]。

正是智能算法在解决信息处理方面的优越性，笔者确定在汽油馏程测定中，尝试使用人工神经网络中的LNN网络；径向基神经网络的广义回归(newgrnn)网络来建立数模和仿真。实验表明，LNN法建立的模型，泛化预测能力强，是一种快速、准确、简便预测汽油馏程蒸发温度可借鉴的方法[5]。

2.2人工神经网络

2.2.1人工神经网络简介

人工神经网络是一类模拟人脑功能的全新数据和知识等信息处理加工系统，是由人工建立的以有向图为拓扑结构的动态系统，通过对连续或断续的输入作状态响应而进行信息处理。神经网络的数学模型是人工神经网络的理论基础。1943年以来，经过了漫长、曲折的发展过程，如今已成为解决复杂信息处理问题，如模式识别、预测、图像处理、函数拟合、优化等的有力工具。

人工神经网络的结构由接收信号的输入层、输出信号的输出层及处于输入层和输出层之间的隐含层组成。人工神经网络的运行可分为两个阶段：①训练或学习阶段；②预测(推广)阶段。在训练或学习阶段，反复向神经网络提供一系列输入—输出模式，并不断调整节点之间的相互连接权重，直至特定的输入产生期望的输出。通过学习或训练后，神经网络便具备(学会)了正确的输入输出响应行为，从而对未知样本进行预报。

2.2.2MATLAB神经网络工具箱概述

MATLAB神经网络工具箱是用MATLAB语言构造出的典型神经网络激活函数,使得人们对所选定网络输出的计算，变成了对激活函数的调用，并按照各种典型的修正网络权重的规则，结合网络的训练过程，用MATLAB编写出各种网络设计与训练的子程序，从而可根据自己的需要，调用所需函数解决实际问题。主要包括的网络模型有：①感知器；②线性网络；③BP网络；④径向基函数；⑤自组织网络；⑥回归网络。对于各种网络模型，工具箱集成了多种学习算法，还给出了大量的示例程序，为用户提供了极大方便。

2.2.3MATLAB神经网络工具箱的应用

实践中常发现，用各种智能方法建立的数学模型对已知数据(即所谓训练集)常能拟合较好，而预报未知样本时，偏差会较大，这就是所谓的“过拟合”(overfiing)现象。反之，由于样本数目过少，建立的模型精度不够，则称之为“欠拟合”(underfiing)。如何提高算法和数学模型的推广能力，以确保预

报结果的可靠性，显然是智能算法中的重要课题。实践表明，用智能算法的神经网络法求解，一是应根据问题的特点选择合适的网络模型；二是建立网络模型时通过仿真，分析判断网络是否适合实际问题的特点，是否达到所需的准确度和精度，这两点至关重要[2-5]。

笔者用神经网络法由汽油馏出温度计算其蒸发温度时，曾选择了LNN网络；径向基神经网络中的广义回归(newgrnn)网络，实验证明，用LNN网络建立的模型，泛化预测能力优于后者。

2.2.4LNN法计算汽油馏程的蒸发温度

2.2.4.1LNN网络简介

LNN网络结构如图1所示，它是一种最简单的神经元网络，由一个或多个线性神经元组成，每个神经元的传递函数为线性函数，可采用Widrow-Hoff学习规则或者LMS(Least Mean Square)算法来调整网络的权重和阈值。

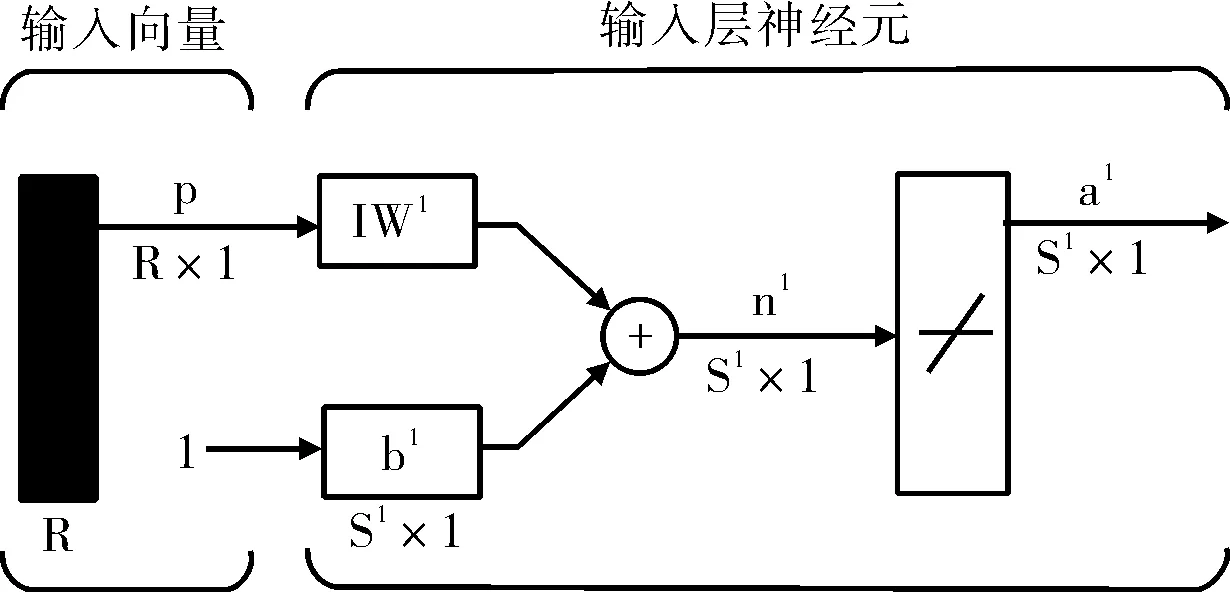
图1　线性神经网络层模型结构图

LNN网络的神经元的传输函数是线性函数，LNN网络层的输出为：

a=purelin(WP+b)=WP+b

LNN网络层的输出可以取任意值，而且线性神经元网络可以是多层的。LNN网络只能求解线性问题，而不能用于非线性计算，这一点与BP网络和径向基网络不同[6-7]。

本文采用newlind函数设计LNN网络。调用格式为：

net=newlind(P,T)

其中：P为训练集网络的输入向量，T为训练集网络的目标向量。

2.2.4.2用LNN法计算汽油馏程的蒸发温度

(1)训练集、测试集试样的确定

取车用汽油馏程测定数据64组，选1～45组作为训练集样本，用来训练建立数学模型，选46～64组共19组作为测试集样本，考察模型的泛化预测能力，见表1、表2。表中馏出温度、蒸发损失量和大气压，为试验测定获得，蒸发温度是按照GB/T6536方法规定得来。

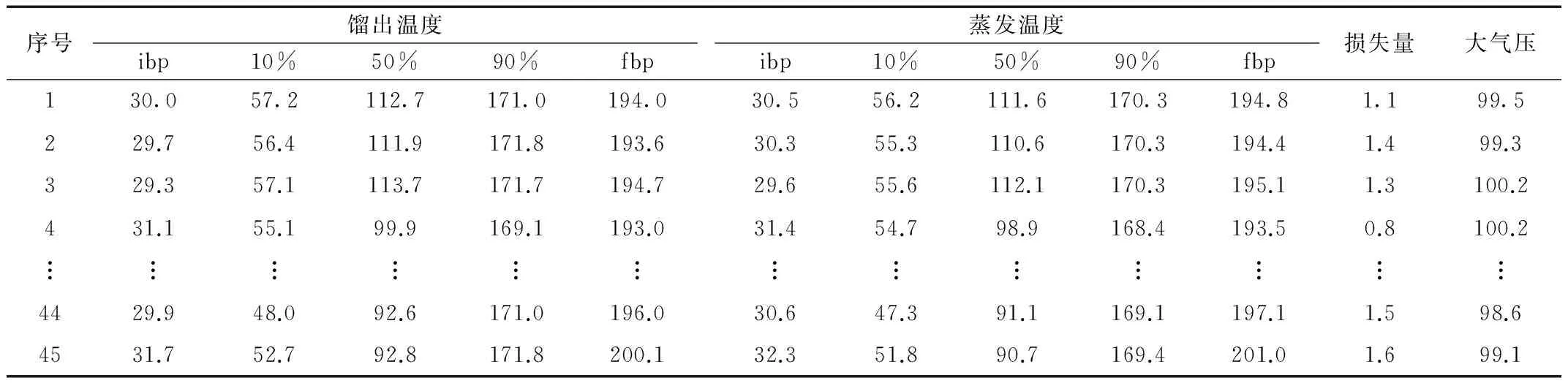
表1　汽油馏程训练集样本数据

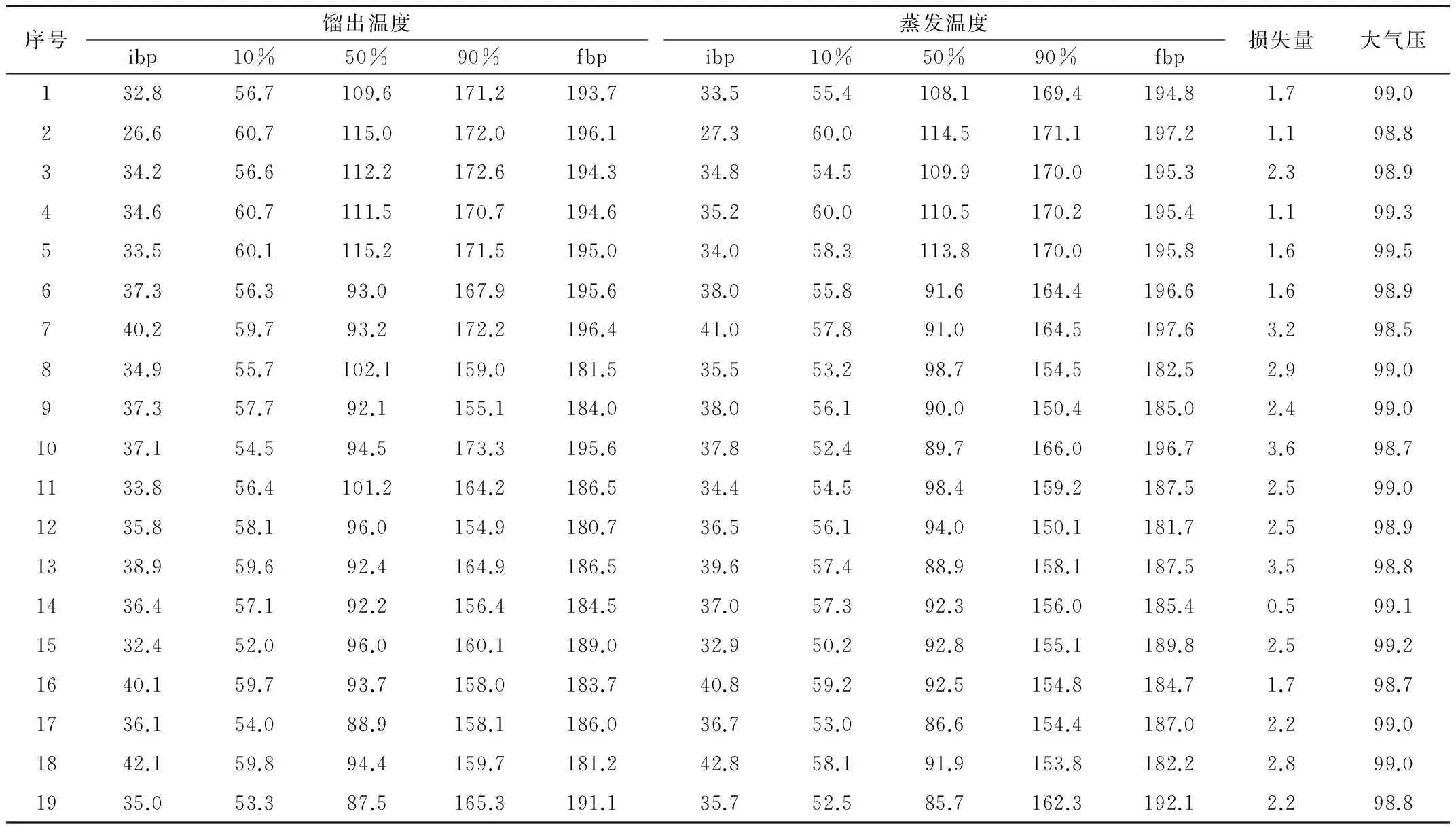
表2　汽油馏程测试集样本数据

(2)LNN算法

用GB/T6536方法从馏出温度计算蒸发温度时，考虑了蒸发损失量和测定时大气压的影响[1]，因此在设计LNN网络结构建立数模时，也考虑了馏出温度、蒸发损失量和测定时大气压的影响。程序设计时，依次把训练集的ibp、10%、50%、90%和fbp点的馏出温度和损失量及大气压作为输入向量，把上述各点的蒸发温度作为目标向量，选择newlind函数设计网络结构，用sim函数仿真，通过训练网络和仿真即可预测蒸发温度。例如将训练集的10%点馏出温度、蒸发损失量和大气压作为输入向量，将对应的10%点蒸发温度作为目标向量，输入电脑，选择newlind函数建立网络，用sim函数仿真，再用测试集的10%点对应的数据考察数模的泛化预测能力，如果对建立的数模满意，就可以在以后测定时，用来预测10%点的蒸发温度。

(3)测试集样本仿真结果与GB/T6536方法测定结果对比

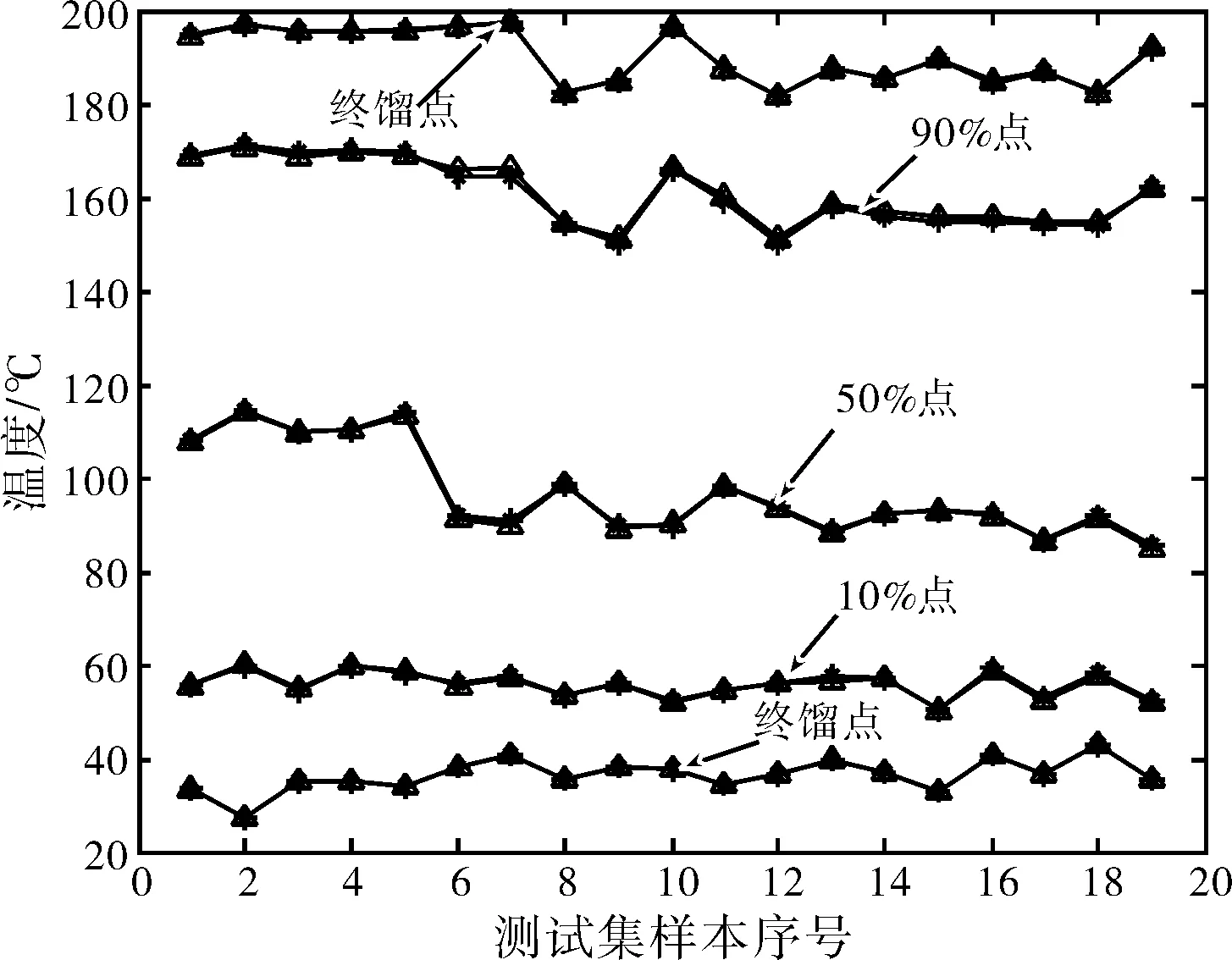
图2　测试集样本各点蒸发温度实测值与仿真值对比图

对比结果见图2。由图2可见，除过90%点的实测值与仿真值偏差稍大以外，ibp、10%、50%、fbp实测值与仿真值偏差均很小。表3列出了测试集样本各点蒸发温度实测值与仿真值的最大绝对偏差，由表3可见，90%点实测值与仿真值偏差稍大，但也未超过2 ℃。

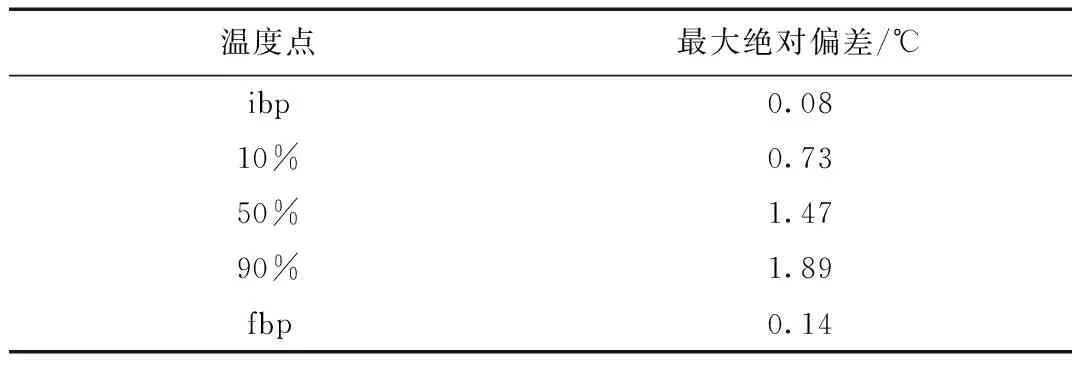
表3　测试集各点蒸发温度实测值与仿真值的最大绝对偏差

(4)LNN法测定结果与径向基广义回归网络法结果的比较

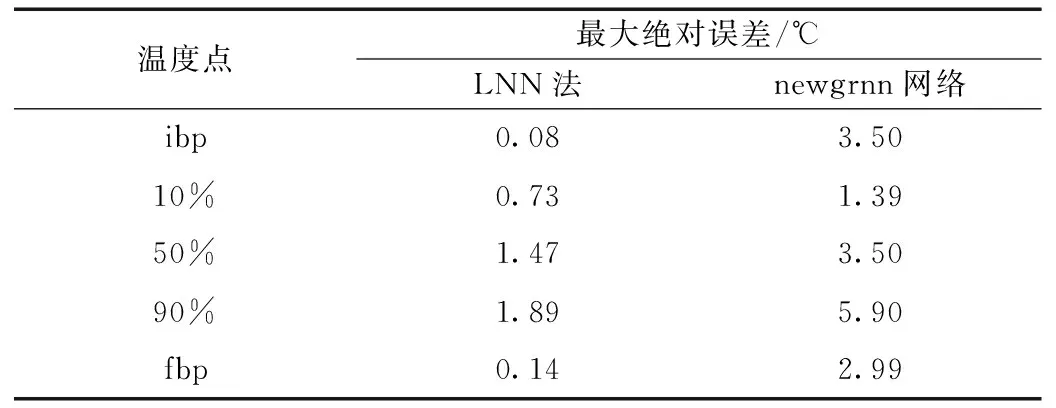
表4　LNN法仿真结果与径向基广义回归网络法仿真结果比较

表4为LNN法测定结果与径向基广义回归网络法结果的比较表。由表可见，LNN法的仿真值与径向基广义回归网络法仿真值比较，前者要优于后者。

(5)LNN法测试的精密度考察

表5为精密度考察表。根据理论分析，汽油馏程蒸发温度测定精密度主要取决于测定过程，而计算机仿真环节，不会带来多大误差，所以测定的精密度和手工测定的精密度相当。

表5　汽油馏程蒸发温度测定精密度考察表(n=5)

注：n=5表示实验时进行了5次平行实验。

3　结　论

(1)实验表明，在使用GB/T6536测定汽油馏程，由馏出温度换算成蒸发温度时，可以使用LNN法。使用时只需要向计算机输入ibp、10%、50%、90%和fbp的馏出温度，蒸发损失量以及测试时的大气压，然后用建立好的线性网络仿真，就可以快速、简便、准确预测出所需的馏程蒸发温度，因此这是一种计算蒸发温度的值得借鉴的方法。

(2)使用人工神经网络法建立数学模型时，一是要注意选择合适的网络模型，二是要调整好网络参数，这样才可以建立泛化预测能力强的数学模型，取得满意的仿真预测结果。

(3)使用LNN法计算馏程蒸发温度，由于观察的温度点减少，操作者工作强度减小，很适合手工操作。

(4)当建立的数学模型使用一段时间后，例如一周或半个月，需要跟使用GB/T6536方法计算的蒸发温度进行对照，对数学模型进行校准、修正，以保证仿真预测结果的可靠性。

[1]国家技术监督局.GB/T6536-2010 石油产品蒸馏测定法[S]．

[2]许国根.模式识别与智能计算的MATLAB实现[M].北京:北京航空航天大学出版社, 2012:5-8.

[3]杨淑莹.群体智能与仿生计算—MATLAB技术实现[M].北京:电子工业出版社, 2012:15-18.

[4]杨淑莹. 模式识别与智能计算—MATLAB实现[M].北京:电子工业出版社, 2008:17-20.

[5]许国根.化学化工中的数学方法及MATLAB实现[M].北京:化学工业出版社, 2008:2-6.

[6]周开利.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社, 2005:10-11.

[7]李水祥,谢文武. MATLAB语言的神经网络工具箱及应用[J]. 高等函授学报(自然科学版), 2007,20(1):43-46.

Calculation of the Evaporation Temperature of Gasoline Distillation by Intelligent Algorithm

ZHANGLiu-yimg,RENYing-ying

(Guangdong Petroleum Company, China Petroleum Chemical Co., Ltd., Guangdong Guangzhou 510000, China)

The method of artificial neural network and radial basis function neural network method was discussed, used for the determination of gasoline distillation test GB/T6536 "Petroleum Products-Determination of distillation", calculating the possibility of evaporation temperature from the distillation temperature. Experiments showed that the generalization of linear neural network prediction ability was better than the RBF neural network. Data was set to establish the mathematical model with the selected training set, test data and simulation results showed that the simulation values of absolute deviation and the original values, was no more than 2 ℃, and it showed that the linear neural network method for calculating the evaporation temperature was feasible, the method was a rapid, accurate, simple and valuable method.

gasoline distillation; evaporation temperature conversion; linear neural network; MATLAB

张柳莺(1981-),女，大学本科，从事油品质检技术工作。

A

1001-9677(2016)010-0134-04