能量因素对压缩空气弹射内弹道性能影响研究

李　军, 胡　亚, 丛龙腾, 周为浩, 于思淼

(南京理工大学 机械工程学院， 南京　210094)



能量因素对压缩空气弹射内弹道性能影响研究

李军, 胡亚, 丛龙腾, 周为浩, 于思淼

(南京理工大学 机械工程学院， 南京210094)

以大口径火箭弹压缩空气发射装置为研究对象,利用理论分析,确定影响内弹道性能的能量因素,并建立了不同空气压力、不同体积以及有、无泄漏的压缩空气弹射内弹道模型。通过对流固耦合数值仿真结果的分析,得到了弹药速度与时间、弹药速度与位移、弹药加速度与时间等关系,从而分析出能量因素对压缩空气弹射内弹道性能的影响。

压缩空气弹射;内弹道性能;能量因素;有限元仿真

0　引　　言

火箭武器的发射方式按照发射动力可以分为冷发射和热发射。冷发射是依靠外部动力使火箭武器弹出发射装置， 在主发动机点火前获得一定初速度的发射[1]。压缩空气弹射是冷发射的代表方式之一， 利用高压空气作用在火箭武器下部提供弹射外力， 从而将火箭武器推出发射装置[2-3]，具有爆发力强及温度适应性广等优势[4]。针对压缩空气弹射内弹道问题， 美苏两国利用各种试验充分研究了压缩空气系统的性能以对其利用[5]。随着压缩空气弹射系统种类逐渐复杂多样， 试验成本增加， 利用试验来研究不同压缩空气弹射系统内弹道性能越来越困难。 近年来， 计算机性能的增加和有限元技术的发展， 使利用虚拟样机技术研究压缩空气弹射成为可能[6]。 本文采用有限元仿真分析方法， 利用双向流固耦合[7]技术研究能量因素对大口径火箭弹压缩空气弹射内弹道性能的影响。

1　大口径火箭弹仿真模型

压缩空气弹射简化模型如图1所示。 整体战术技术要求火箭弹在发射管管口的速度v0达到200 m/s， 发射装置高压室压缩空气压强为25～35 MPa， 取中间值30 MPa为初始压强P0， 初始容积V0为0.2 m3， 整体发射装置长度L不得超过12 m。 由于在模型仿真中无法准确判断发射装置的总长， 以火箭弹达到v0时的位移l与高压室段长度之和替代L， 以火箭弹弹底位于高压室出口时刻为初始时刻t0。发射管管壁壁厚为30 mm， 火箭弹直径为275 mm。

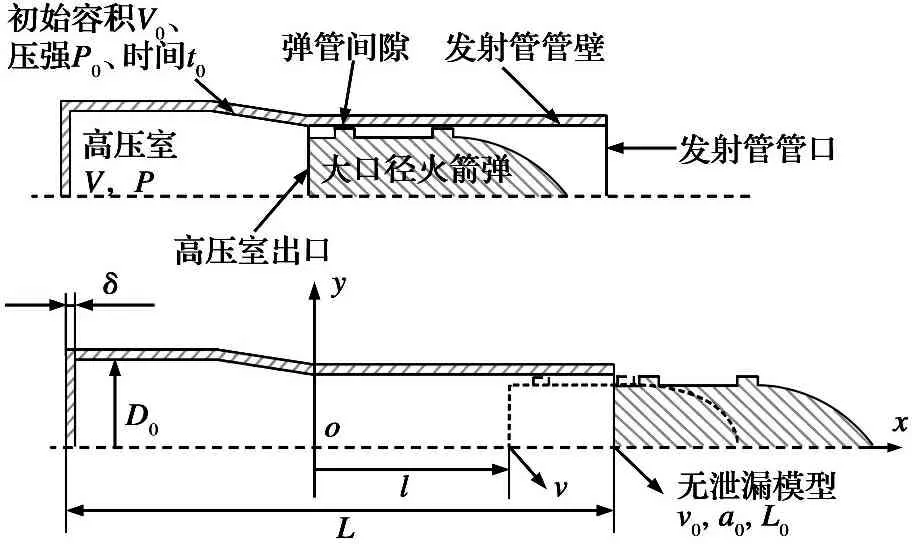
图1压缩空气弹射示意图

为了更好地达到战术技术要求， 实现最佳的内弹道性能， 需要分析影响内弹道的因素， 并且将压缩空气能量最大利用， 如何确定压缩空气能量的影响因素是本文的重点。

2　压缩弹射有效能

按照热力学定律描述， 流动空气的绝对能量由焓、 运动能和势能组成， 起决定作用的是流动空气的焓， 其运动能和势能基本可以忽略不计[8]。 焓又由流动空气的内能和传递能组成。流动空气的能量组成可表示为

H=U+pV=mCpθ

(1)

式中：H为系统能量;U为内能;p为目标空气压强;V为目标空气体积;m为空气质量；Cp为等压比热；θ为空气绝对温度。

参照式(1)， 空气的绝对能量取决于空气的质量和温度， 与空气压力无关。 空气质量越大、 温度越高， 能量越大。 因此， 即使是周围的大气也具有很大的能量。

但这与越压缩空气压强越大， 能量就越大的观点存在悖论， 究其原因， 是因为压缩空气能量体现形式是伴随空气体积的压缩或者膨胀而增减， 是与绝对能量不同的性质概念， 所以焓不能用来表示储存于压缩空气中用于动力传动的能量。

因此需要定义压缩空气对外的做功能力， 即压缩空气的有效能。 在该定义的基础上， 有效能是一个相对于大气状态基准量的相对量(亦可以相当于其他压强状态)， 是建立在压缩空气弹射系统工况相较于标准大气系统基础之上的。 压缩空气的有效能E可以表示为

(2)

式中：pa外界环境压力。

可以看出影响内弹道性能的能量因素主要包含高压室压缩空气压强和体积， 除此之外在实际发射装置中， 火箭弹和发射管之间存在间隙， 所以在压缩空气弹射时作用在火箭弹弹底的高压气体必然存在由于泄漏造成的能量损失, 从而影响内弹道性能[9]。下面逐一探讨三个主要因素对内弹道的影响。

3　能量因素对内弹道性能的影响

3.1压强对冷发射装置内弹道性能的影响

在有限元软件中建立双向流固耦合仿真模型， 在合理的压强范围内， 取P0(30 MPa)附近的四组压强25 MPa， 28 MPa， 32 MPa， 35 MPa的压缩空气模型进行比较， 弹底位移l和速度v对应结果如图2所示。

图2不同压强下模型弹底速度-位移曲线

由图2可以看出， 随着压强的增加， 速度和位移都明显增加， 并且在足够长的距离和相应的时间都可以达到v0的战术技术要求。此外， 随着位移的增加， 不同压强之间的速度差距逐渐增大。在相同的压强下， 同一曲线的斜率逐渐减小， 即速度随位移的增加量逐渐减小。不同压强模型的发射装置总长L如表1所示。

表1　不同压强模型发射装置总长

表1中， 最大的L数值对应的是25 MPa模型， 发射装置总长约为11 m， 处于发射装置总长度的临界点， 符合战术要求， 因此在总长度上所有压强模型均符合战术技术要求。在合理的压强范围内比较， 随着压强的增大， 压强增加量分别为3 MPa， 2 MPa， 2 MPa， 3 MPa， 而位移减少量则为2 m， 0.86 m， 0.67 m， 0.75 m， 说明压强对位移减少量的贡献也逐渐减少, 进而说明随着压强的逐渐增加， 压缩空气能量的损失也越大， 因此理论上压强越小越好。综合考虑发射装置总长度及能量损失， 确定最佳模型压强为28 MPa。

3.2高压室容积对冷发射装置内弹道性能的影响

高压室容积同压强一样是决定压缩空气有效能的主要因素， 本文采用等差扩大发射装置体积的方法考虑容积因素对发射装置内弹道的影响， 扩大体积采用保证高压室长度不变， 扩大内径的方法， 在初始内径D0的基础上逐渐增加， 分别达到1.1， 1.2， 1.3， 1.4， 1.5， 1.6倍的V0， 在对比模型中压缩空气压强均为P0， 仿真后得到弹底的速度-时间曲线和位移-时间曲线如图3(a)～(b)所示。

图3不同容积模型下弹底速度-时间及位移-时间曲线

由图3可以看出， 速度和位移随着体积的增大而相应增加， 但曲线间差异较小， 说明10%的体积增加量对动力学结果并没有产生很大影响。由于最小体积V0已达到战术技术要求， 那么其他不同体积对比模型能在更短距离达到200 m/s， 相应发射装置总长度更短。不同容积模型的发射装置总长如表2所示。

由表2可以看出， 体积以0.02 m3的等差增大。 随着高压室容积的增大， 位移的减少量依次为0.49 m， 0.33 m， 0.32 m， 0.24 m， 0.17 m， 0.15 m， 说明随着容积的增大， 其对发射装置总长度的影响逐渐减小。

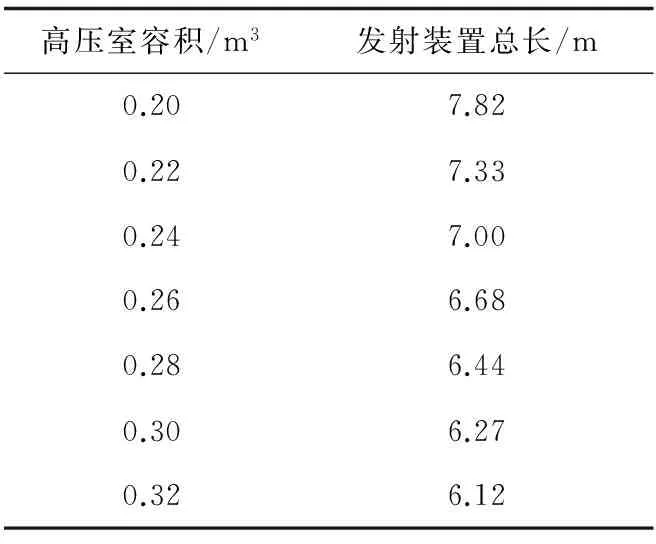
表2　不同高压室容积模型发射装置总长

3.3泄漏面积对冷发射装置内弹道性能的影响

火箭弹的尾部横截面积与发射管通气面积之差称为泄漏面积， 也就是环形的间隙面积， 取决于弹管间间隙。 根据文献[10]， 采用0.005 m2作为本次模型的泄漏面积。

在确定泄漏模型弹管间隙的条件下， 对无泄漏模型和泄漏模型进行有限元仿真分析， 得出的对比结果如图4(a)～(b)所示。

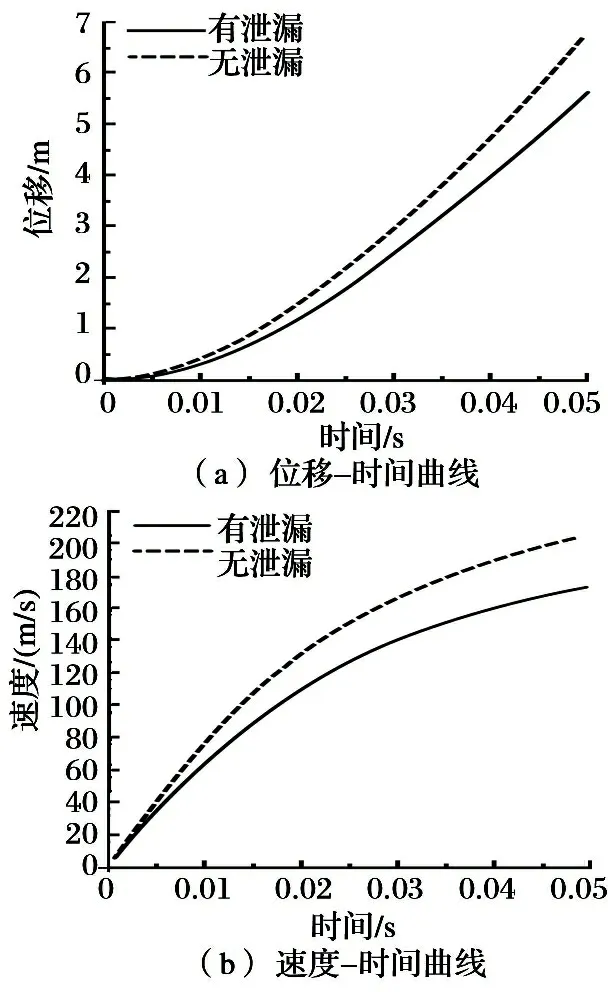
图4有、 无泄漏模型弹底位移-时间及速度-时间曲线

由图4可以看出， 在无泄漏模型速度达到v0时刻， 无泄漏模型的速度是泄漏模型的1.11倍， 位移为1.14倍， 泄漏使能量大量消耗。与其他能量因素相比， 泄漏对内弹道性能影响较大。

为具体分析加速度情况， 得出的加速度-位移曲线如图5所示。

由图5可以看出， 随着火箭弹前进， 其加速度

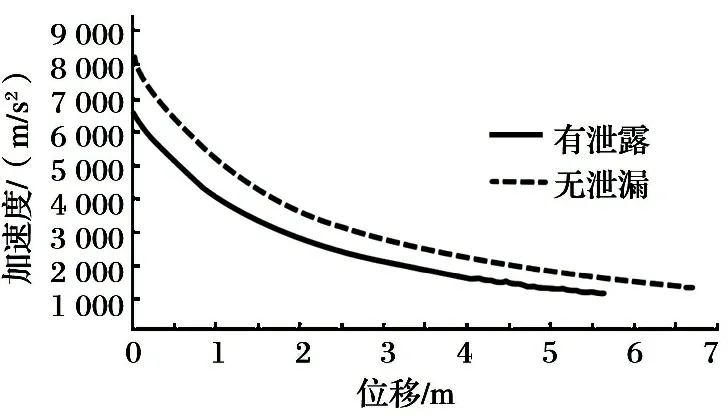
图5有、 无泄漏模型弹底加速度-位移曲线

在不断减小。 从曲线上下间隔的趋势可以得出， 随着位移的增加，两模型的火箭弹加速度差异在减小。 这说明随着压缩空气压强的降低， 泄漏面积对内弹道性能的影响也在减弱， 其造成的能量损失也相应降低。

无泄漏模型与泄漏模型对比结果如表3所示。

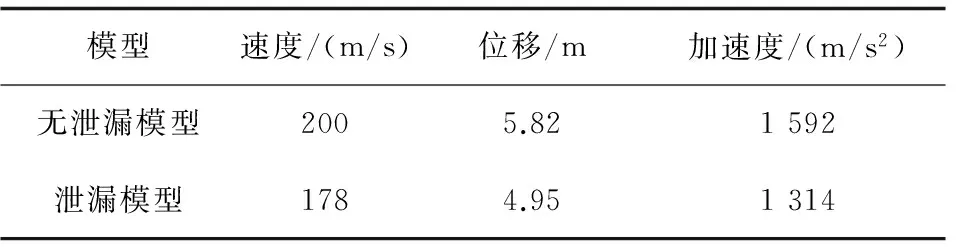
表3　无泄漏模型与泄漏模型结果对比

为定量确定能量的损失情况， 从无泄漏模型达到v0时刻的两者动力学数值对比得出：从能量上来看， 无泄漏模型达到v0的火箭弹具有的动能为4×106J， 而泄漏模型的火箭弹具有的动能为3.17×106J， 能量损耗大约为1/4。

所以若按照泄漏面积0.005 m2来看， 压缩空气的能量会很大损耗， 由于发射装置和火箭弹相对固定， 因此不能要求改变发射管结构或者火箭弹尺寸来减小弹管间隙。为减小泄漏面积， 除了增加火箭弹弹体的加工精度外， 还可采用增加密封装置来减小泄漏面积， 如在火箭弹弹体上增加密封圈， 或者在火箭弹弹底增加类似活塞的火箭弹托体， 以减少能量损耗。

4　结　　论

本文通过有限元仿真得出压缩空气压强、 高压室容积及泄漏面积等能量因素对内弹道性能的影响， 总结如下：

(1) 随着压缩空气压强增加， 压强对内弹道性能的影响减小。高压室压强在合理范围内， 压强越大， 能量利用率越低；

(2) 随着高压室容积的增加， 容积对内弹道性能的影响减小。在满足战术要求条件下， 高压室容积越小， 能量利用率越高；

(3) 泄漏会导致压缩空气能量大量损耗， 0.005 m2的泄漏面积会导致近1/4的能量损耗， 对内弹道性能的影响较大， 可通过增加密封装置减少因泄漏导致的能量损耗。

[1] 周子林. 战略导弹的冷发射技术[J]. 国外导弹与宇航， 1980(10): 1-9.

[2] 芮守祯, 邢玉明. 几种导弹弹射动力系统内弹道性能比较[J]. 北京航空航天大学学报, 2009，35(6): 766-770.

[3] 李文盛. 舞剑向苍穹——浅谈防空导弹发射方式[J]. 兵器知识, 2011(11): 42-45.

[4] 丛龙腾，姜超， 鲁霄光，等. 基于AUTODYN的压缩空气弹射内弹道研究[J]. 航空兵器, 2014(5): 46-49.

[5] 岳峰. 国外舰空导弹武器系统现状及发展趋势[J]. 飞航导弹, 2012(8): 57-61.

[6] Panciroli R. Water Entry of Flexible Wedges: Some Issues on the FSI Phenomena[J]. Applied Ocean Research, 2013, 39(1)： 72-74.

[7] 刘玉磊. 燃气舵流固耦合传热数值分析[J]. 航空兵器, 2013(3): 41-43.

[8] 蔡茂林. 现代气动技术理论与实践第四讲：压缩空气的能量[J]. 液压气动与密封, 2007， 27(5): 54-59.

[9] 方九如. 超近程防御系统压缩空气发射装置分析[D]. 南京： 南京理工大学, 2014.

[10] 乔汝椿. 轻型舰载鱼雷发射装置漏泄空气能量计算[J]. 鱼雷技术, 1999(1): 33-35.

Study on the Influence of Energy Factors on the Interior Ballistic Performance of Compressed Air Ejection

Li Jun, Hu Ya, Cong Longteng, Zhou Weihao, Yu Simiao

(School of Mechanical Engineering， Nanjing University of Science & Technology， Nanjing 210094， China)

For studying the compressed air ejection device of large-caliber rocket projectiles, the theoretical analysis is used to identify energy factors that influence the interior ballistic performance, and interior ballistic models of compressed air ejection are set up based on different air pressure, different volume, leakage and no leakage. Through analyzing the numerical simulation results of fluid-solid coupling, the relationships among ammunition velocity and time, ammunition velocity and displacement, ammunition acceleration and time are got, and the influences of energy factors on the interior ballistic performance of compressed air ejection are acquired.

compressed air ejection； interior ballistic performance； energy factors； finite element simulation

10.19297/j.cnki.41-1228/tj.2016.03.016

2015-09-30

李军(1965-)， 男， 河南平顶山人， 教授， 研究方向为火箭导弹发射技术。

TJ768

A

1673-5048(2016)03-0071-04