科赫雪花孔的衍射图案
邱为钢
(湖州师范学院理学院,浙江 湖州 313000)
科赫雪花孔的衍射图案
邱为钢
(湖州师范学院理学院,浙江 湖州313000)
假设光波是标量波,对衍射孔作格点剖分,文章给出了接受屏上光强度的格点求和计算表达式.对零到四级科赫雪花孔图形作正方形格点剖分,对四级科赫雪花孔图形作正三角形格点剖分,数值计算得到了科赫雪花孔的衍射图案.计算结果发现,衍射图案保持了科赫雪花的对称性,并给出了衍射图案对称性细节.
科赫雪花;衍射
平面波通过特殊形状衍射屏后的衍射图案的研究,是波动光学教学研究的一个热点.这些形状包括方孔[1]、正三角形与正六边形孔[2]、康托分形[3]、斯宾基三角形[4]等.衍射振幅与孔的傅里叶变换有关,保持了孔的对称性[5].科赫雪花[6]也是一个典型的分形物体,平面波通过科赫雪花孔,衍射图案有什么特征,具有哪些对称性?这就是本文主要探讨的问题.
形成科赫雪花的操作如下:先从一个正三角形开始,每一条边中间选两点,向外作一个等边三角形,然后把两点之间的线段去掉,再对每一条边作同样的操作,依次迭代下去,直至无穷,最终得到的图形就是科赫雪花.图1是零到三次迭代操作的图形.
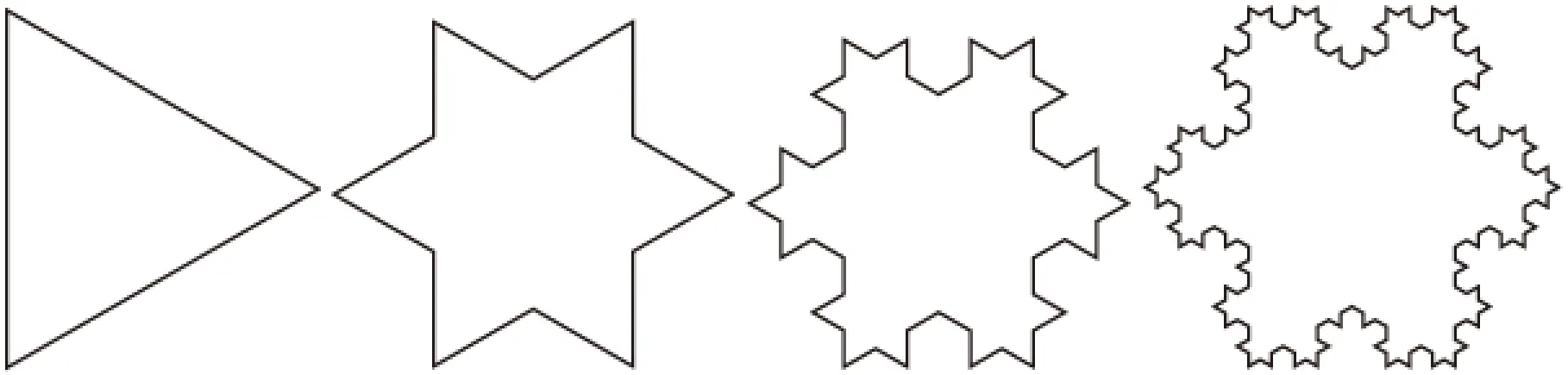
图1 零到三级科赫雪花

(1)
这一点的强度为
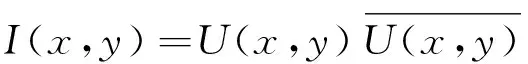
(2)
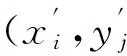
(3)
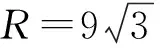
格点选取也有两种方法,第一种是正方形格点,数值计算得到正方形格点剖分对应的衍射图案如图2~图5所示.
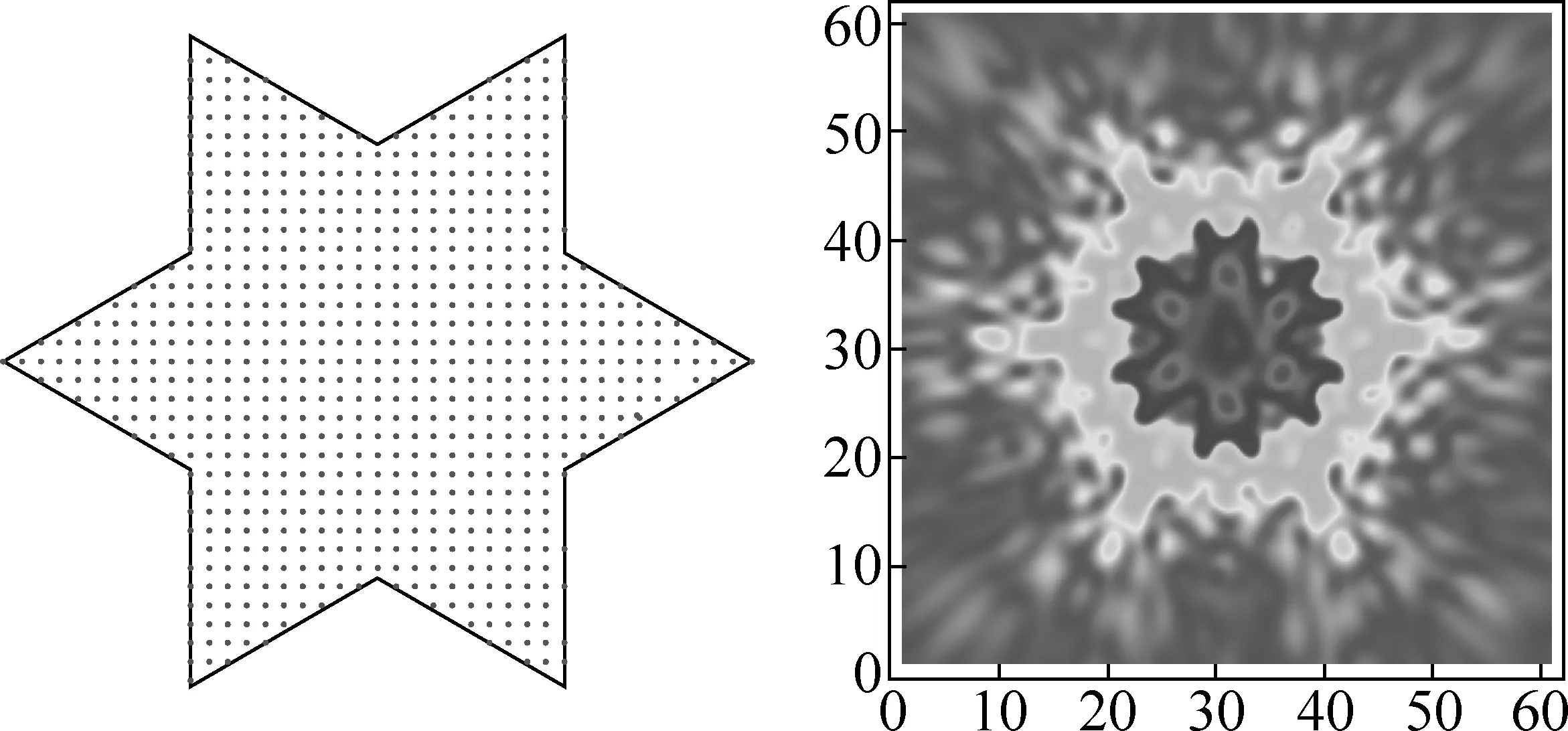
图2 正方形格点剖分一级科赫雪花孔的衍射图案
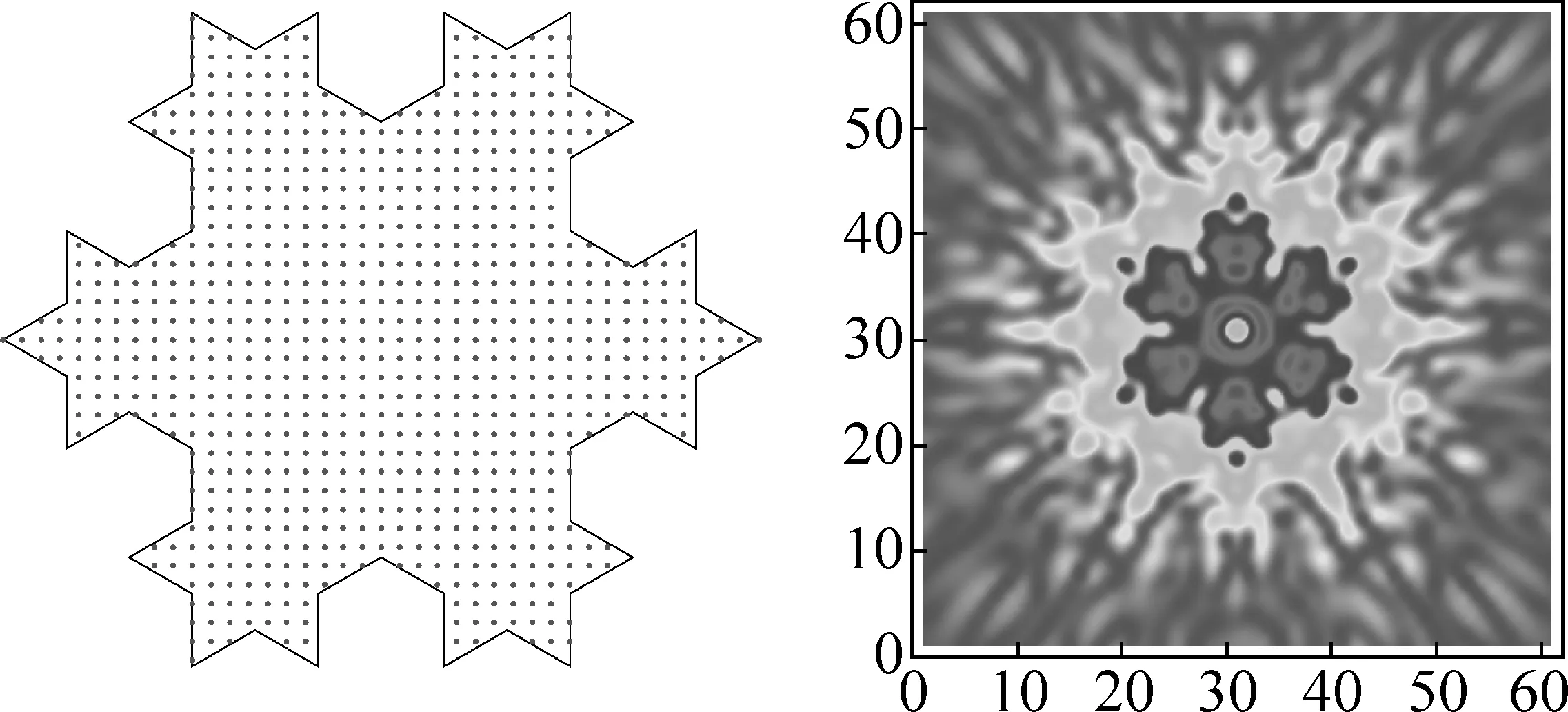
图3 正方形格点剖分二级科赫雪花孔的衍射图案
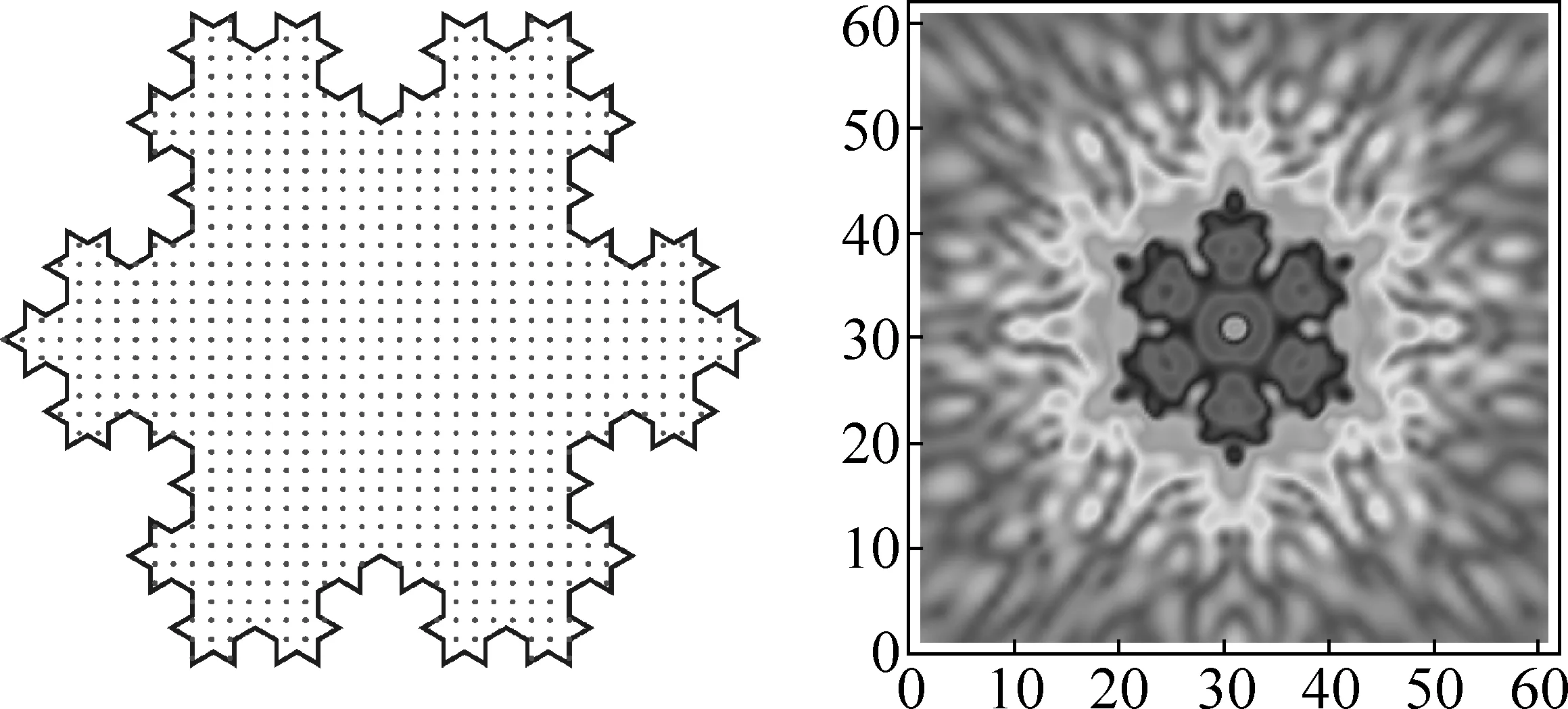
图4 正方形格点剖分三级科赫雪花孔的衍射图案
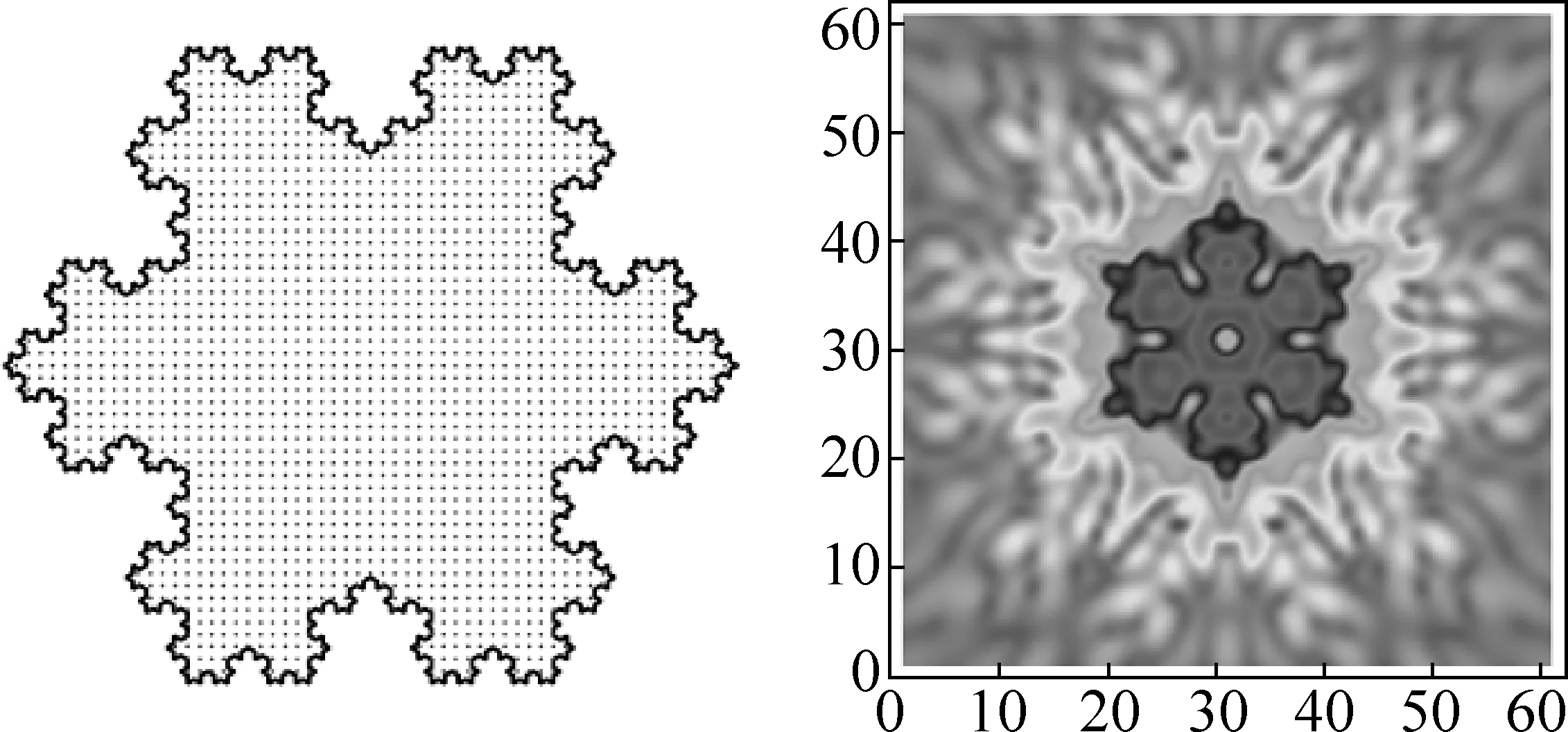
图5 正方形格点剖分四级科赫雪花孔的衍射图案
第二种格点选取是正三角形格点,保持原有各级近似科赫雪花的对称性,四级科赫雪花的格点分布和衍射图案如图6所示.
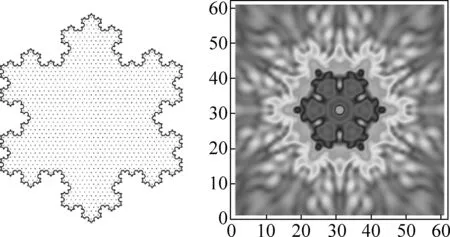
图6 正三角形格点四级科赫雪花孔的衍射图案
由图2~图5可以看出,衍射图案保持原有孔的对称性,即正三角形对称性.衍射图案与原有孔还有“互补”关系.即如果原有孔有一部分是凹陷的,那么衍射图案在相应位置是凸出的.图5中的正方形格点有1883个,图6中正三角形格点有1261个,对于四级科赫雪花孔,两种格点剖分得到衍射图案一样,都保持科赫雪花的对称性:旋转对称和反射对称.
这样,利用简化的衍射振幅表达式,选取正方形和正三角形格点剖分,求和近似代替积分,数值计算得到了零到四级科赫雪花孔的衍射图案,这些图案保持了原有图形的对称性.
[1]刘东州,侯志青,刘立芳.方孔夫琅禾费衍射的数值模拟[J].大学物理,2011,30(4):38-42.
[2]郑建华,梁华秋,周小莉.正三角形与正六边形夫琅和费衍射光强分布[J].光学仪器,2005,27(5):106-108.
[3]李平.Cantor型分形光栅的夫琅禾费衍射特性研究[J].大学物理,2002,21(11):11-14.
[4]田磊,戴冬云,刘生华.互补Sierpinski 地毯光栅夫琅和费衍射现象的研究[J].应用光学,2005,26(5):17-20.
[5]戴又善.二维小孔的对称变换与夫琅禾费衍射光强分布[J].大学物理,2011,30(11):22-27.
[6]科赫雪花[EB/OL][2015-09-03]http://mathworld.wolfram.com/KochSnowflake.html.
■
THE DIFFRACTION PATERN OF KOCH SNOWFLAKE HOLE
Qiu Weigang
(School of Science, Huzhou Teachers College, Huzhou, Zhejiang 313000)
Assuming the light wave is a scalar wave and making a lattice subdivision of the diffraction hole, the finite summation expression of light intensity distribution on the accept screen is given. The numerical solution of diffraction pattern is obtained from the square and equilateral triangle lattice subdivision of the Koch snowflake hole from zero to forth order. Results show that the diffraction patterns keep the original symmetry of Koch snowflake, and also present some special symmetry details in the diffraction patterns.
Koch snowflake; diffraction
2015-04-22;
2015-09-15
国家自然科学基金(11475062,11275067).
邱为钢,男,副教授,主要从事大学物理的教学和研究.wgqiu@hutc.zj.cn
引文格式: 邱为钢. 科赫雪花孔的衍射图案[J]. 物理与工程,2016,26(3):18-19,23.

