两类图在球面和环面上的嵌入
刘新求
(湖南工程职业技术学院基础课部,中国 长沙 410151)
两类图在球面和环面上的嵌入
刘新求*
(湖南工程职业技术学院基础课部,中国 长沙410151)
图在不同亏格曲面上的嵌入往往有相关关系, 因此, 分析一些图类在小亏格曲面上的嵌入是一项有意义的工作. 本文利用刘彦佩教授提出的嵌入的联树模型研究了两类图在球面和环面上的嵌入特征,分别得到了它们的嵌入个数.
曲面; 亏格; 嵌入; 联树
本文中关于曲面、嵌入和亏格等概念均与文献[1]一致. 图的曲面嵌入是拓扑图论的一个重要分支, 特别地, 研究图在不同亏格曲面上的嵌入个数即图的亏格分布和完全亏格分布问题是其中重要研究方向之一. 上世纪九十年代起, 国内外很多学者做出了一些有价值的研究[2-7], 但是还远远未解决这个问题, 对于大部分图类, 还不能得出其亏格分布和完全亏格分布, 此问题被证明为NP难问题. 于是, 有学者转而研究一些图在特定曲面上的嵌入, 譬如研究图在球面、射影平面、环面及Klein平面等小亏格曲面上的嵌入. 近年来, 利用刘彦佩教授提出的联树模型和曲面运算理论[8], 国内一些学者在这方面做出了一些有意义的结论[9-11].本文作者亦在联树模型的基础上, 研究了两类项链图在射影平面上的嵌入[12], 本文拟在此基础上, 进一步研究两类图在球面和环面上的嵌入.
1 曲面运算理论和联树模型
为了表述方便, 本文对曲面运算理论和联树模型进行简要介绍[8].
曲面运算理论:任何一个曲面都可以看作是由一个正多边形“粘合”而成, 所以曲面可以用多边形来表示, 具体的表示理论参考文献[8]. 下面仅列出本文叙述中要用到的三种运算和三种关系.
运算1Aaa-⟺A.
运算2AabBab⟺AcBc.
运算3AB⟺(Aa)(a-B).
以上三种运算不改变曲面的类型. 由这三种运算, 导出曲面的三种拓扑等价关系:
关系1AaBbCa-Db-E~ADCBEaba-b-.
关系2AaBaC~AB-Caa.
关系3Aaabcb-c-~Aaabbcc.
运用以上三种运算和三种关系, 任何一个曲面都可以化为标准型代数表示:


联树模型[8]:联树模型是刘彦佩教授创立的一种研究图的曲面嵌入的新方法. 这种方法可以如下概述: (1) 合理选择生成树; (2) 切断余树边,得到联树; (3) 标记余树边, 按旋系走遍, 记录余树边得到关联曲面. 关联曲面的亏格为k, 既表明在此旋系下, 图G嵌入在亏格为k的可定向或不可定向曲面上. 图的曲面嵌入和关联曲面之间一一对应.
2 引理和定义
定义1若可定向曲面S=AaBbCa-Db-, 则称边a和b在曲面S中交错, 若可定向曲面S=AaBa-CbDb-, 则称边a和b在曲面S中平行.
引理1[8]若曲面S1是可定向曲面且亏格为p, 曲面S=S1aba-b-, 则曲面S的可定向亏格为p+1.



根据引理1,S的亏格至少为1,与S是球面矛盾,所以A中边的下标应该是从大到小,从而
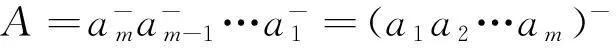
充分性显然.
从以上引理可知,一个曲面是球面当且仅当曲面中任意两条边均平行.
引理3[9]设A是a1,a2,…,am的线性序,曲面S=a1a2…amA~O1, 则线性序A有
种不同的排序.
定义2在两个节点之间连结m(m≥2)条重边构成的图叫做双极图,记作Dm.

图1 图Dm及其联树Fig.1 Graph Dm and its joint tree
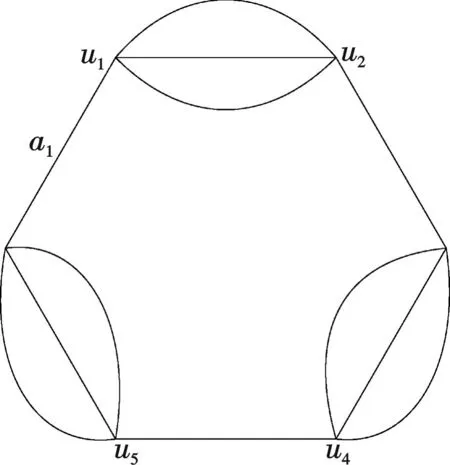
图2 图Fig.

3 主要结论
定理1双极图Dm在球面上的嵌入个数为(m-1)!.
证如图1, 选择边am作为生成树, 切断余树边a1,a2,…,am-1, 得到联树. 一个点的旋有(m-1)!个, 如图所示, 固定双极图左边点的旋, 则得到双极图Dm的关联曲面S=a1a2…am-1A, 其中A表示右边点的旋, 是a1,a2,…,am-1的线性序. 根据引理2.2可知, 双极图Dm在球面上的嵌入个数为(m-1)!.
定理2双极图Dm(m≥3)在环面上的嵌入个数是
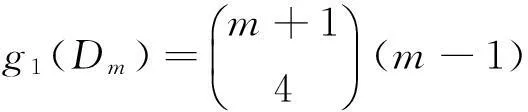

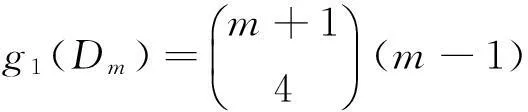



图3 图的联树Fig.3 Graph and its joint tree

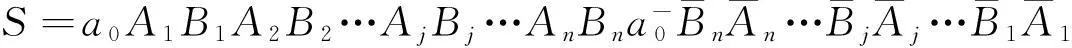



证嵌入情形1E1,E2,…,En中的每条边均与a0平行.

同样地, 固定节点u2i-1:i=1,2,…,n的旋, 对于i≠j, 根据引理2, 节点u2i的旋唯一确定. 所以关联曲面中Ei(i≠j)中边的放置方法均为m!种.



综上, 嵌入情形1在环面上的嵌入个数为

嵌入情形2E1,E2,…,En中至少有一条边与a0交错.
设Ej(1≤j≤n) 中有一条边与a0交错, 则Ej与a0组成的子列Sj有下列子情形:
嵌入情形2.1Ej中与a0交错的边相互平行.

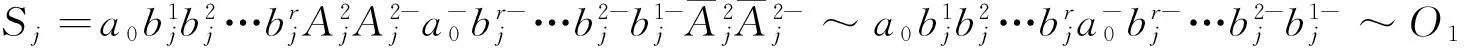
或者





而Ei(i≠j) 的边的放置方法有(m-1)m!+m!=mm! 种.
综上, 嵌入情形2.1 在环面上的嵌入个数为
(mn-1)(m!)n.
嵌入情形2.2Ej中与a0交错的边至少有两条互相交错.
嵌入子情形2.2.1



方程
的非负整数解的个数为

所以Ej的边的放置方法有

而Ei(i≠j) 的边的放置方法均为m!, 所以此嵌入子情形在环面上的嵌入个数为

嵌入子情形2.2.2

嵌入子情形2.2.2 在环面上的嵌入个数等同于嵌入子情形2.2.1.
嵌入子情形2.2.3

嵌入子情形2.2.3 在环面上的嵌入个数亦等同于嵌入子情形2.2.1.
则把这三种嵌入子情形相加即得到嵌入情形2.2的总嵌入个数为

把以上嵌入情形的嵌入个数相加即得定理结论.
[1]GROSS J L, TUCKER T W. Topological graph theory[M]. New York: Dover Publicaions, Inc, 1987.
[2]GROSS J L, FURST M L. Hierarchy of imbedding distribution invariants of graph[J]. J Graph Theory, 1987,11:205-220.
[3]GURST M L, GROSS J L, STATEMAN R. Genus distributions for two classes of graphs[J]. J Combin Theory Ser B, 1989,46:22-36.
[4]GROSS J L, ROBBINS D P, TUCKER T W. Genus distributions for bouquets of circles[J]. J Combin Theory Ser B, 1989,47:292-306.
[5]KWAK J H, LEE J. Genus polynomials of dippoles of circles[J]. Discrete Math, 1993,33:115-125.
[6]CHEN J, GROSS J L, RIEPER R G. Overlap matrics and total imbedding distrbution[J]. Discrete Math, 1994,128:73-94.
[7]CHEN Y C, LIU Y P. The total embedding distributions of cacti and necklaces[J]. Acta Math Sinica (Eng Ser), 2006,22(5):1583-1590.
[8]刘彦佩. 地图的代数原理[M]. 北京:高等教育出版社, 2006.
[9]杨艳, 刘彦佩. 两类四正则图的完全亏格分布[J]. 数学学报, 2007,50(5):1190-1200.
[10]赵喜梅, 刘彦佩. 类圈图的亏格分布[J]. 数学物理学报, 2008,28(4):757-767.
[11]魏白, 黄元秋, 郭婷, 等. 一类图在小亏格曲面上的嵌入[J]. 湖南师范大学自然科学学报, 2012,35(5):24-29.
[12]刘新求, 黄元秋. 两类项链图在射影平面上的嵌入[J]. 数学物理学报, 2011,31(3):601-610.
(编辑HWJ)
The Embedding of Two Type Graphs on the Sphere and Torus
LIU Xin-qiu*
(Basic Courses Department, Hunan Vocational Technical College of Engineering, Changsha 410151, China)
Embedding numbers of graphs on distinct genus surfaces are always related. Therefore, analyzing embedding numbers of graphs on lower genus surfaces is important to determine their genus distributions and total genus distributions. Based on the model of joint tree introduced by Liu, this paper calculates the embedding number of two type graphs on sphere and torus.
surface; genus; embedding; joint tree
10.7612/j.issn.1000-2537.2016.03.013
2015-04-19基金项目:国家自然科学基金资助项目(11371133; 61370172;11471106) ;湖南省教育厅科学研究资助项目(13C200)*通讯作者,E-mail:liuxinqiuxie@sina.com
O157.5
A
1000-2537(2016)03-0075-05

