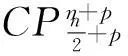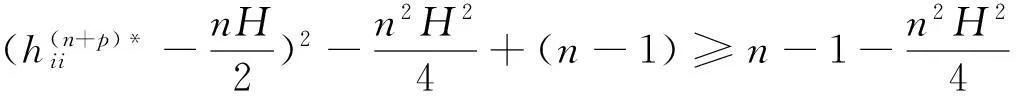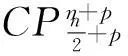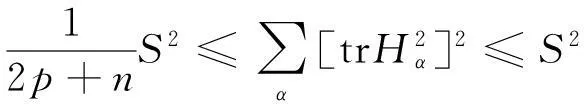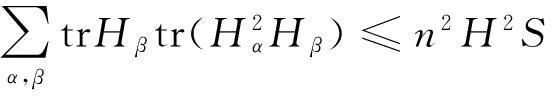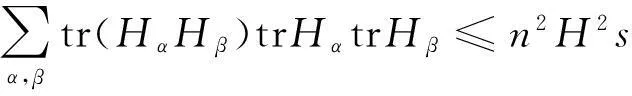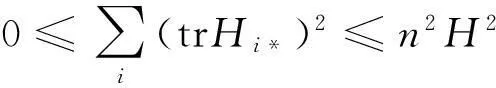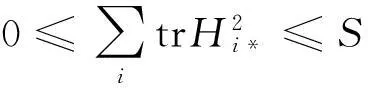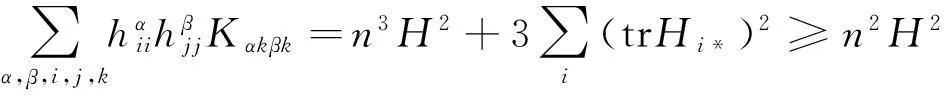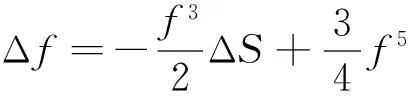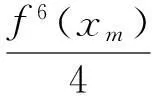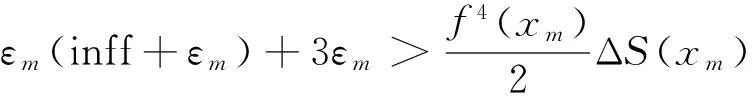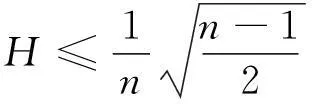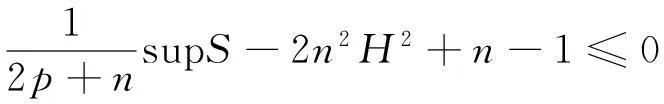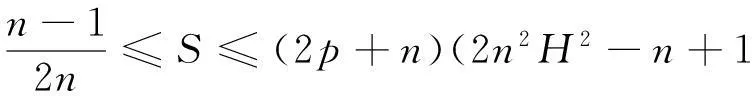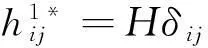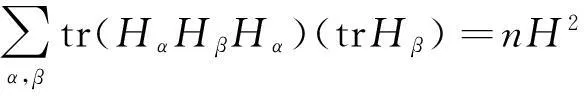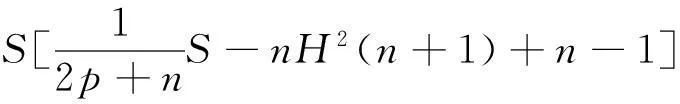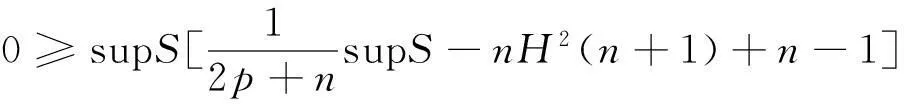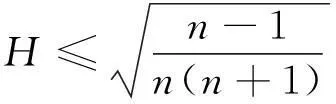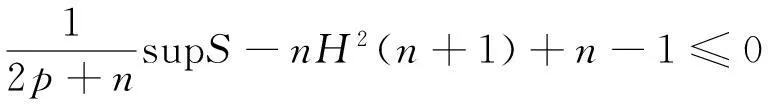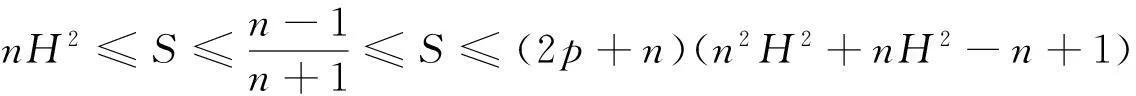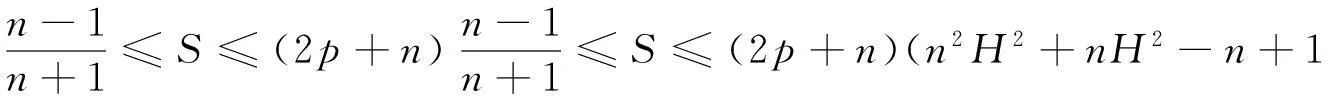不定复空间型中具有常数量曲率的完备全实2-调和类空子流形

陈亚力，宋卫东

(安徽师范大学数学计算机科学学院，中国 芜湖　241000)



不定复空间型中具有常数量曲率的完备全实2-调和类空子流形

陈亚力*，宋卫东

(安徽师范大学数学计算机科学学院，中国 芜湖241000)

不定复空间；完备；2-调和；类空

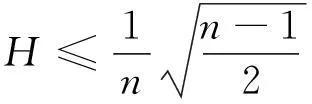
当H=0,p=0时，与文献[5]结论一致.

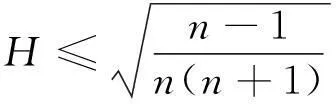
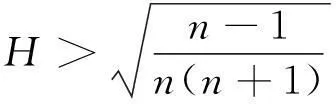
当H=0,p=0时，与文献[5]结论一致.

1　基本公式和引理

e1,…,en+p,e1*,…,e(n+p)*,

使得限制于Mn时，{e1,…,en}与Mn相切.本文约定各类指标取值范围

A,B,C,…=1,…,n+p,1*,…,(n+p)*;i,j,k,…=1,…,n;α,β,γ,…=n+1,…,n+p,1*,…,(n+p)*.

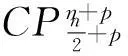
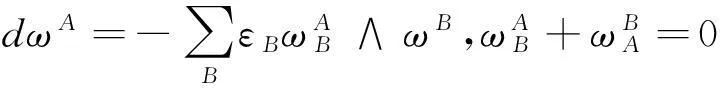
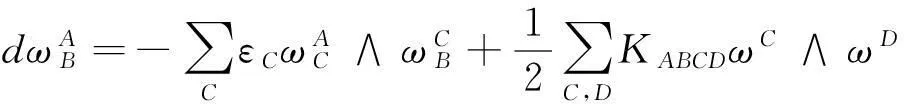
其中

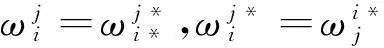
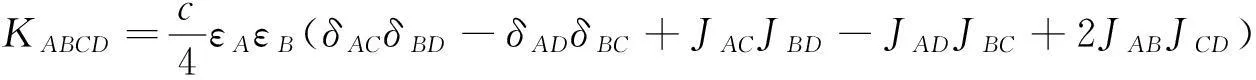
这里(JAB)为线性变换J关于{eA}的变换矩阵.

限制在Mn上有[8]

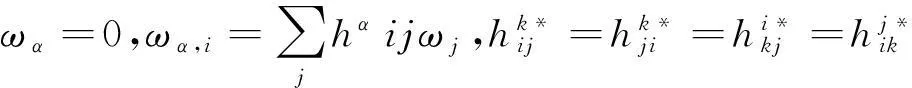
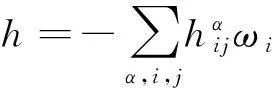
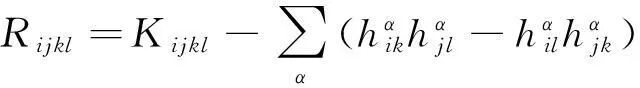
(1)

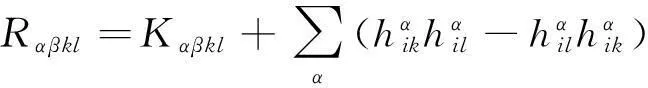
若以R表示Mn的标准数量曲率，则有

n(n-1)R=n(n-1)-n2H2+S,

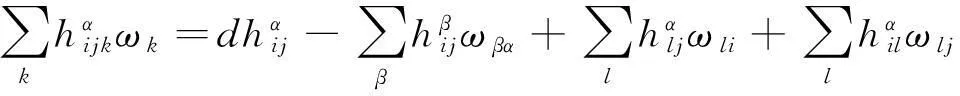
trHα=0,(α≠(n+p)*),

由文献[10]有，

(2)

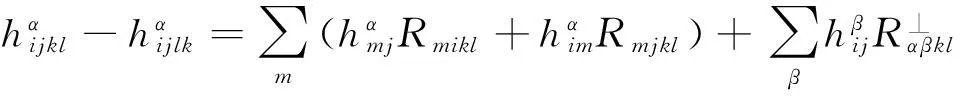
由上述公式不难计算：

因此

(3)

2　定理的证明

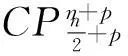
(4)

(5)

由式(4)及式(2)可得(4)改写成

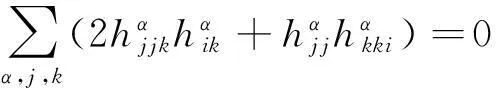
将此式两端关于指标i求共变导数，并关于i求和，得

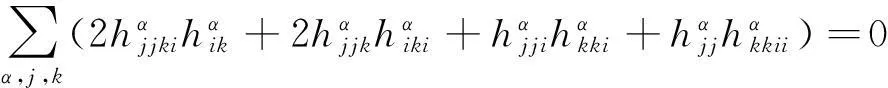
调整式(5)指标，可得

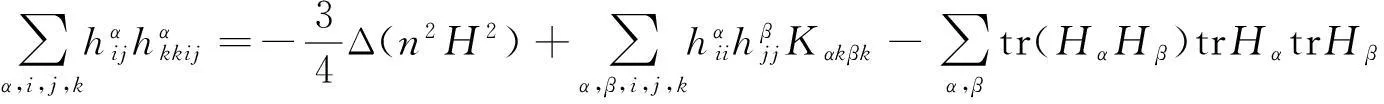
引理2[12-13]设Mn是Ricci曲率有下界的完备黎曼流形，f是Mn上C2类有界函数，则对∀ε>0,都存在一点x∈Mn,使得在x处

‖gradf‖≤ε,Δf>-ε,f(x)

证由式(1),

水泥砂浆试件为正方体试件，边长为70.7 mm。胶砂比为1∶2，水灰比包括3种，即0.55、0.60和0.65。试件经标准养护28 d后，然后放到冻融试验机内进行冻融。冻融温度为±20℃，当冻融循环次数分别为0次、25次和50次后，将试件取出进行单轴压缩试验。在进行单轴压缩试验时，加载的应变速率分为4种，即分别为10-2 s-1、10-3 s-1、10-4 s-1和10-5 s-1。

定理1的证明由式(3).

(6)

其中

(7)

(8)

(9)

(10)

由于R为常数,

ΔS=Δ(n2H2).

(11)

由上述各式可知，

(12)

(13)

由引理3可知，f满足引理2的条件，对任意序列εm,εm>0且εm→0(m→∞),都存在Mn上的一点列xm,使得

(14)

由式(13)和式(14)可以看到，

(15)

当εm→0时，f(x)达到下确界，S(x)达到上确界，在式(15)中令m→∞，结合式(12)得

(16)

由上式可知，若-2n2H2+n-1≥0,即

必有Mn全测地.

那么，

nH2≤S≤(2p+n)(2n2H2-n+1),

即

定理1证毕.

定理2的证明Mn是伪脐的，即

(17)

由式(6),(7),(8),(9),(10),(11),(17)可得

(18)

和定理1证明同理，应用引理2结合式(15)和式(18)可得，

(19)

由式(19)可知，若-nH2(n+1)+n-1≥0,即

必有Mn全测地.

那么，

即

定理2证毕.

[1]CHOI Y S, KWON J H, SUH Y J. On semi-Ryan complex submanifolds in an indefinite complex space form[J]. Rocky Moun J Math, 2001,31(3):873-897.

[2]KENDALL D G. Shape manifolds, procrustean metrics, and complex projective spaces[J]. Bull London Math Soc, 1984,16(2): 81-121.

[3]DONG Y. On indefinite special Lagrangian submanifolds in indefinite complex Euclidean spaces[J]. J Geom Phys, 2009,59(6):710-726.

[4]ERDEM S, GLAZEBROOK J F. Harmonic maps of Riemann surfaces to indefinite complex hyperbolic and projective spaces[J]. Proc London Math Soc, 1983,3(3):547-562.

[5]孙华飞.不定复空间型中的全实极大类空子流形[J].东北大学学报, 1994,15(5):547-550.

[6]VRANCKEN L. Minimal Lagrangian submanifolds with constant sectional curvature in indefinite complex space forms[J]. Proc Am Math Soc, 2002,130(5):1459-1466.

[7]CHENG Q. Complete space-like submanifolds in a de Sitter space with parallel mean curvature vector[J]. Math Zeit, 1991,206(1):333-339.

[8]YAU S T. Submanifolds with constant mean curvature[J]. Am J Math, 1974,96(2):346-366.

[9]CHEN B, OGIUE K. On totally real submanifolds[J]. Trans Am Math Soc, 1974,193:257-266.

[10]ROMERO A, SUH Y J. Dierential geometry of indefinite complex submanifolds in indefinite complex space forms[J]. Extr Math, 2004,19(3):339-398.

[11]欧阳崇珍.伪黎曼空间型的2-调和类空子流形[J].数学年刊：A辑, 2000,21(6):649-654.

[12]OMORI H. Isometric immersions of Riemannian manifolds[J]. J Math Soc Jap, 1967,19(2):205-214.

[13]YAU S T. Harmonic functions on complete Riemannian manifolds[J]. Comm Pure Appl Math, 1975,28(2):201-228.

[14]纪永强.子流形几何[M].北京：科学出版社, 2003.

(编辑HWJ)

Indefinite Complex Space form with Constant Scalar Curvature in a Complete Totally Real Space-Like Biharmonic Submanifold

CHEN Ya-li*, SONG Wei-dong

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

indefinite complex space form; complete; biharmonic; space-like

10.7612/j.issn.1000-2537.2016.03.012

2016-03-04基金项目：安徽省教育厅自然科学研究重点项目(KJ2010A125)；安徽师范大学科研培育基金(2016XJJ017)*通讯作者,E-mail：chenylwuhu@qq.com

O186.15

A

1000-2537(2016)03-0069-06