一种快速高精度的零件图像配准算法*

苏　森　李郁峰　范　勇　陈念年　刘冬冬

(西南科技大学计算机科学与技术学院, 四川 绵阳621010)



一种快速高精度的零件图像配准算法*

四川省教育厅重大培育项目(14CZ0012)

苏森李郁峰范勇陈念年刘冬冬

(西南科技大学计算机科学与技术学院, 四川 绵阳621010)

针对大批量机械加工零件测量时图像配准精度低、速度慢的问题，提出了一种快速高精度零件图像配准算法，分初始配准和精确配准两个过程。初始配准采用零件最小外接矩形和图像形心，以缩减配准参数范围提高配准速度。精确配准将互信息作为相似度准则，利用空间位置一致时互信息值最大实现参数最佳定位提高配准精度。实验结果表明，对于2048×2048像素的机械加工零件图片，算法配准平移量精度达到像素级，配准角度误差不超过0.1°，配准时间小于2.1 s，满足实际连续测量中大批量零件配准要求。

图像配准;最小外接矩形;形心;互信息

在线、连续、自动化测量已成为机械加工零件测量的发展趋势，其中大批量零件测量中，图像配准的精度及速度会严重影响零件测量的准确度和效率，故图像配准是机械加工零件连续测量关键技术之一。图像配准是对不同时间、不同视场、不同成像模式的两幅或多幅图像进行空间几何变换，使得图像在几何上能够匹配对应起来。

目前，国内外研究学者将图像配准大致分为两类，基于灰度信息法和特征法。灰度信息法主要有互信息法[1-4]、相位相关法等[5]，该类方法不需要对图像灰度间的关系作任何假设，也不需要对图像进行预处理，具有较高的准确性和鲁棒性，但需考虑匹配点邻域灰度，配准时计算量大，耗时长。特征配准法主要有SUSAN角点[6]检测、Harris角点[7]检测、SIFT特征点[8-10]检测，通过提取图像特征点，大大压缩图像信息，故配准时计算简单，速度快，但需较多的人工介入，且机械零件特征匹配时很容易误匹配，致使配准精度较低。

为了满足大批量机械加工零件图像配准精度高、速度快的要求，本文将互信息作为相似度准则，利用零件最小外接矩形和形心，提出了一种快速、高精度的配准算法。该算法结合灰度信息法的高精度特性，忽略局部细节信息，从整体形态分析，通过4次整体位置变换即能确定最佳配准参数信息，在保证精度的同时也大大缩减了计算时间。

1　算法总体设计方案

若点(x1,y1)、(x2,y2)，分别为参考图像和待配准图像中对应两点，则它们之间应满足如下关系：

(1)

其中：θ为配准角度；tx、ty为配准平移量。在大批量零件图像配准中，其难点是在保证精度的前提下，如何快速获取配准参数，从而提高配准速度。为此，本文结合机械零件图像特征，将整个配准过程分为初始配准与精确配准两个过程，算法流程如图1所示。

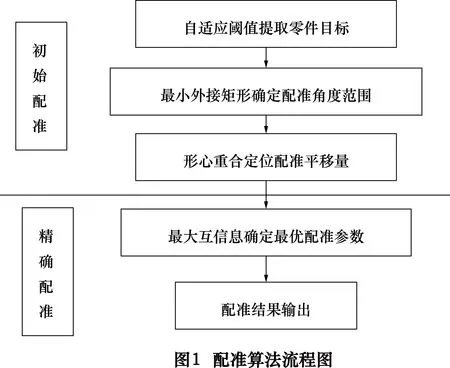
(1)初始配准：缩减配准参数范围以提高配准速度。

首先对零件图像进行自适应阈值分割提取零件目标；其次，对零件目标进行边缘轮廓追踪，获取其对应的最小外接矩形，根据矩形与水平轴夹角关系，获得四种配准角度；最后，将处于不同角度的零件图像按照形心为参照，得到图像配准过程的平移参数。

(2)精确配准：获取最佳配准参数以提高配准精度。

初始配准虽然能够快速确定配准角度和配准平移量参数范围，但无法得出最优解，因此，本文将互信息作为相似度准则，以初始配准结果作为精确配准的输入，根据参考图像和待配准图像空间位置一致时互信息值最大，确定最佳的配准角度和配准平移量。

2　初始配准

2.1自适应阈值分割

机械零件图像背景和前景区别比较大，且图像中目标比较单一，如图2a所示。为此，直接采用最大类间方差(Otsu)算法求取最佳阈值T，其计算式为：

σ(t)2=ω1(t)×ω2(t)[μ1(t)-μ2(t)]2

(2)

式中：ω1(t)、ω2(t)分别为灰度值小于T的C1类和大于T的C2类占整幅图像的比例，μ1(t)、μ2(t)分别为C1，C2和的平均灰度；σ(t)2为C1和C2之间的方差。让T在[0,L]内依次取值，使σ(t)2最大即为最佳阈值，并利用式(3)实现二值化分割。其中g(x,y)为二值化图像，f(x,y)为原始图像，L为灰度级。分割结果如图2b所示。

(3)

2.2最小外接矩形确定配准角度范围

针对零件图像最小外接矩形可以近似描述零件旋转角度的特点，本文采取Canny边缘检查算法提取零件图像轮廓，得到轮廓数据s(q1,q2…,qn)，然后通过Graham算法构造零件凸包，根据凸包求取最小外接矩形，利用最小外接矩形最短边与水平轴夹角关系确定配准角度范围。

2.2.1最小外接矩形

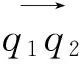
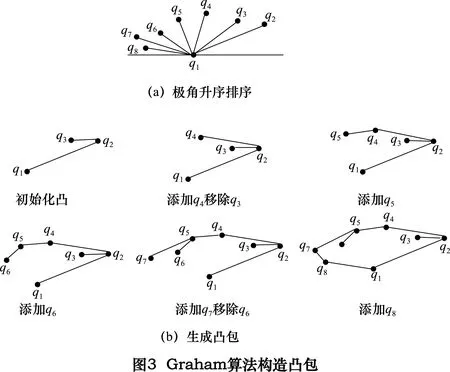
2.2.2配准角度范围获取

构成零件图像最小外接矩形四点坐标，计算其最短边与水平轴夹角θ(逆时针为正方向)，如图4所示。根据式(3)得出待配准图像4b和参考图像4a之间配准角度关系。

Δθ=θ2-θ1

(3)

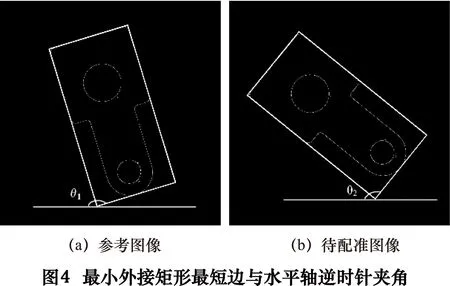
在用最短边与水平轴夹角确定配准角度时，待配准图像可能会出现图5所示的3种情况。为此，真实配准角度可能为Δθ、Δθ+90°、Δθ+180°、Δθ+270°的其中一个。因此，将上述四种角度作为配准角度的范围。

2.3形心重合定位配准平移量

二维零件图像，形心有且仅有一个。因此，通过零件形心差值，可以快速得出配准平移关系。形心是通过对二维图像处理和计算确定目标中心位置，对于二值化图像g(x,y)，其行、列坐标计算目标形心坐标公式如(4)、(5)。式(6)中(Δx，Δy)为配准平移量，即待配准图像形心(xc2,yc2)和参考图像形心(xc1,yc1)的差值。

(4)

(5)

Δx=xc2-xc1Δy=yc2-yc1

(6)

3　精确配准

3.1互信息理论

互信息是信息论中的一个测度，用来衡量两个随机变量之间的依赖程度。对于参考图像A和待配准图像B，其互信息定义为：

(7)

式中：I(A,B)表示两幅图像间的互信息值；PA和PB(b)是灰度a和灰度b在图像A和图像B出现的概率；PAB(a,b)是灰度a和灰度b在两幅图像同一位置出现的概率。其PA(a)、PB(b)、PAB(a,b)可由归一化联合直方图表示：

(8)

PB(b)=∑aPAB(a,b)

(9)

PA(a)=∑bPAB(a,b)

(10)

式中：h(a,b)表示两幅图像的联合直方图。

3.2最大互信息确定最优配准参数

两幅图像精确配准时，互信息值达到最大，即可通过求取最大互信息值确定最优配准参数。算法描述如下：

(1)将待配准图像B旋转φk度，其中φkφ[Δθ，Δθ+90°、Δθ+180°、Δθ+270°]，k[1,2,3,4]。根据式(5)～(7)求取旋转后待配准图像Bφk和参考图像A的形心差值(Δxφk,Δyφk)。

(2)利用式(11)平移待配准图像形心Bφk(x2,y2)与参考图像形心A(x1,y1)重合，此时待配准图像为B＇φk

(11)

(4)当K>4时，跳转到步骤5，否则重复以上步骤。

4　实验结果

为评价本文配准算法在大批量零件配准时的有效性，选取大小为2048×2048像素的图像2a作为参考图像，对参考图像在[-10，10]像素、[-10°，10°]范围内随机平移旋转得到浮动图像并与参考图像进行21次配准，整个实验过程将从配准精度和配准时间两方面与目前主流配准算法进行对比，即基于特征法中的Sift特征点配准算法和基于互信息的Powell算法。实验在Inter(R)Core(TM)i3-3240CPU@3.40GHz内存4GB的计算机上测试。

4.1配准算法精度和时间效率比较

Sift算法是一种提取局部特征的算法，在尺度空间寻找特征点，利用匹配特征点作为配准依据，计算出反向映射得到配准参数；基于互信息的Powell算法是一种局部优化算法，该算法轮流对配准参数进行优化，使互信息达到最大从而完成配准过程。

从表1实验结果可知，Sift算法配准精度最差，水平方向和垂直方向误差达到180个像素。因为在提取机械零件特征点时，局部特殊点的缺失和特征点的误匹配降低了配准精度。基于互信息的Powell算法采用整幅图像灰度信息进行迭代搜索，相比Sift算法配准精度有了较大提高，但需在水平、垂直和旋转角度3个方向上进行大量迭代，增加了计算复杂度，降低了配准效率，无法满足实时在线配准要求。

本文将互信息作为相识度准则，从整体形态分析，利用最小外接矩形最短边与坐标轴夹角关系和图像形心位置信息，得到图像配准参数。与前两种算法相比，本文算法无需提取特征点，从而避免了由于特征点误匹配对配准精度的影响，提高了配准精度，再则，本文从整体入手，4次位置变化即能完成配准过程，配准效率大大提高。

表1配准算法结果比较

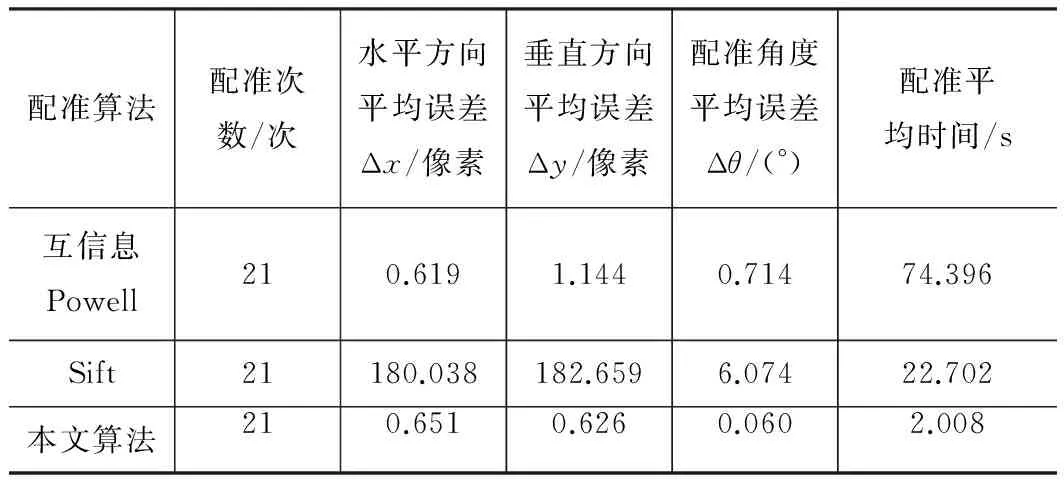
配准算法配准次数/次水平方向平均误差Δx/像素垂直方向平均误差Δy/像素配准角度平均误差Δθ/(°)配准平均时间/s互信息Powell210.6191.1440.71474.396Sift21180.038182.6596.07422.702本文算法210.6510.6260.0602.008

4.2连续测量中配准引入的测量误差

为了验证在连续测量中采用本文算法对待配准图像配准后引入的测量误差较小，将图6a所示零件作为参考图像进行几何测量，并选取3种不同方位的待配准图像通过配准后再次测量，测量结果与参考图像测量结果进行比较，测量误差如表2所示。

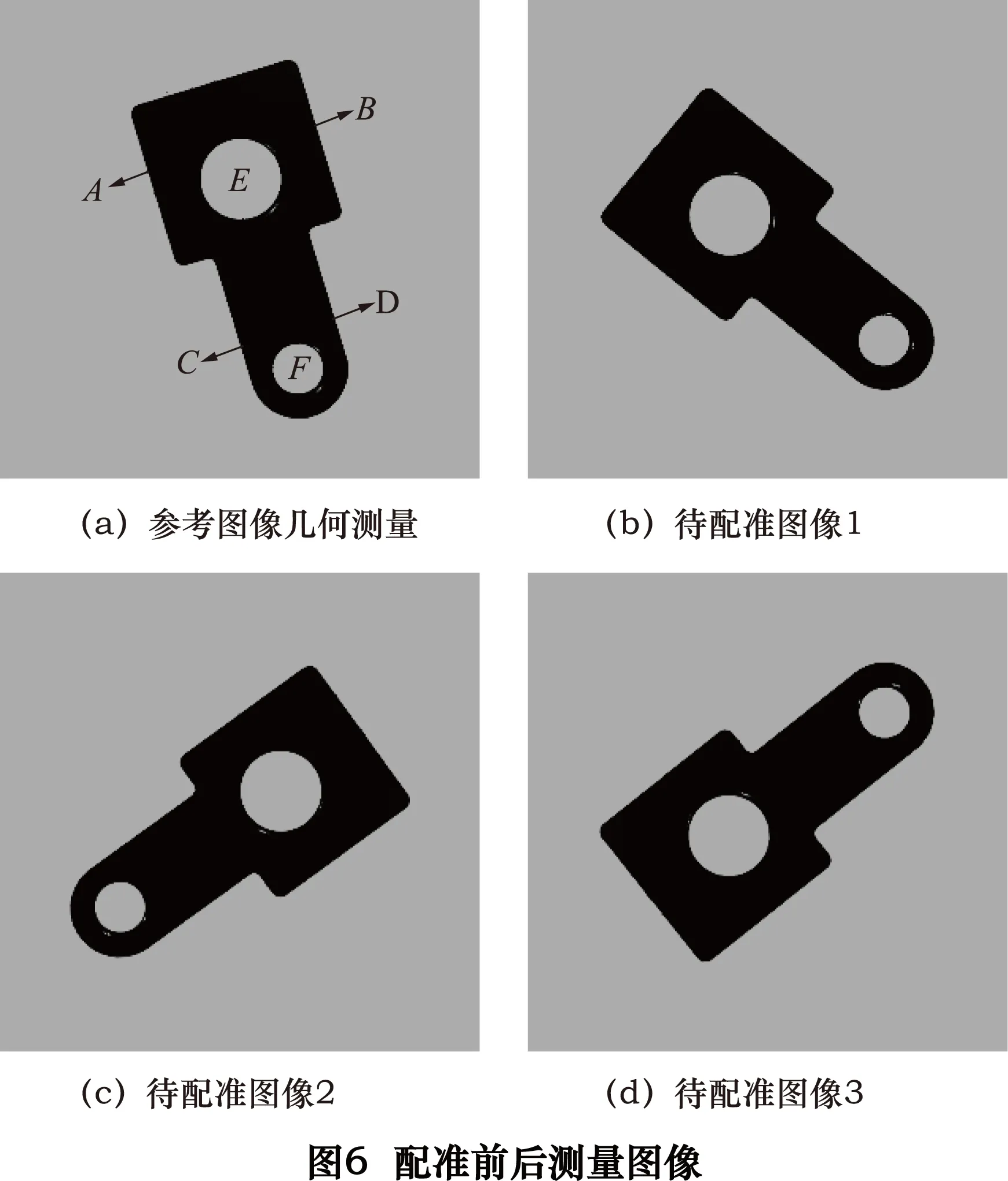
表2待图像配准后几何测量误差

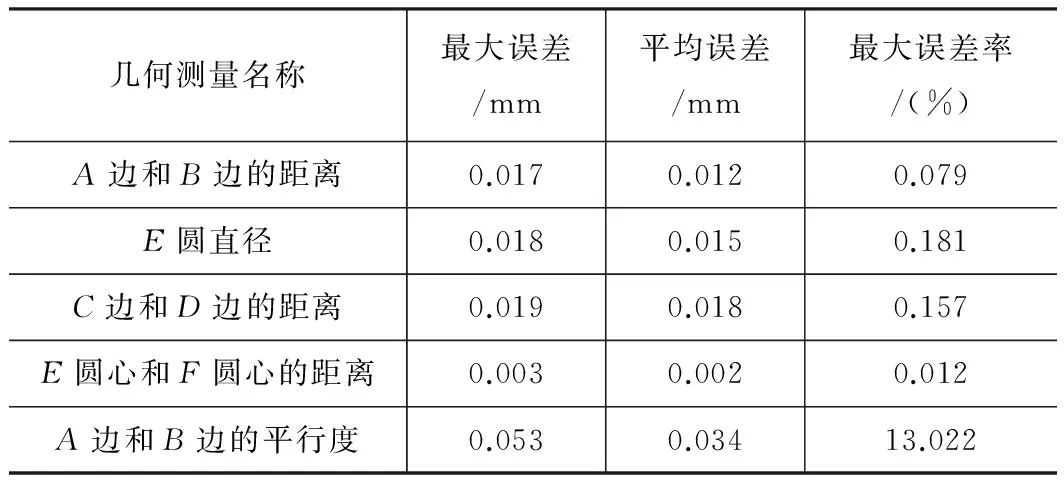
几何测量名称最大误差/mm平均误差/mm最大误差率/(%)A边和B边的距离0.0170.0120.079E圆直径0.0180.0150.181C边和D边的距离0.0190.0180.157E圆心和F圆心的距离0.0030.0020.012A边和B边的平行度0.0530.03413.022

从表2可知，配准前后测量最大误差在53 μm以内，表明待配准图像通过配准后相对参考图像测量变化极小。这是由于该算法不依赖局部信息，从整体形态出发，利用最小外接矩形和形心反映两幅图像位置关系，从而避免局部无效特征信息对配准结果的影响，提高了配准精度，减小了测量误差。

5　结语

本文结合大批量零件图像配准的实际要求，提出了一种快速高精度的零件图像配准算法，分为初始配准和精确配准两步。在初始配准中采用包含零件最小外接矩形和图像形心，快速获取配准参数范围以提高配准速度。在精确配准中将互信息作为相似度准则，利用最大互信息原理得到最优配准参数，提高配准精度。实验结果表明，与目前主流的配准算法相比，该算法配准速度快，配准精度高，是一种有效的自动配准方法。

[1]Klein S, Staring M, Pluim J P W. Evaluation of optimization methods for nonrigid medical image registration using mutual information and B-splines[J]. Image Processing, IEEE Transactions on, 2007, 16(12): 2879-2890.

[2]Loeckx D, Slagmolen P, Maes F, et al. Nonrigid image registration using conditional mutual information[J]. Medical Imaging, IEEE Transactions on, 2010, 29(1): 19-29.

[3]魏玉兰,颜云辉,李兵,等. 邻域灰度与空间特征相结合的互信息配准方法研究[J]. 中国机械工程,2011,22(4):439-443.

[4]冯雪芳,吴锡生. 基于归一化边缘互信息与自适应加速粒子群的图像配准方法[J]. 计算机工程与科学,2013(1):119-123.

[5]施云飞,朱国富,罗鹏飞. 基于相位相关法的SAR图像配准[J]. 计算机仿真,2007(9):210-213.

[6]文杨天,李征,吴仲光. 基于SUSAN算法的图像配准[J]. 计算机应用,2006(10):2380-2382.

[7]常丽萍,冀小平,赵梁. 分块的基于Harris角点检测的图像配准方法[J]. 电视技术,2013(1):45-47.

[8]赵萌萌,曹建秋. 基于边缘角点的SIFT图像配准算法[J]. 重庆交通大学学报：自然科学版,2013(4):721-724.

[9]刘辉,申海龙. 一种基于改进SIFT算法的图像配准方法[J]. 微电子学与计算机,2014(1):38-42.

[10]范宗杰,徐向辉,周晓丽. 一种基于SIFT算法的SAR图像配准方法[J]. 电子测量技术,2014(8):70-74.

(编辑谭弘颖)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

A fast and accurate image registration method for parts

SU Sen, LI Yufen, FAN Yong,CHEN Niannian,LIU Dongdong

(School of Computer Science and Technology, Southwest University of Science and Technology, Mianyang 621010, CHN)

In view of the precision of image registration and the slow speed of registration in the measurement of large quantities of machining parts, this paper presents a fast and accurate image registration algorithm for parts, which is divided into two processes: the initial registration and the accurate registration. First step is to use parts of the minimum bounding rectangle and the image centroid, reducing the scale of the registration parameters in order to improve the speed of registration. Second step is to use Mutual information as the similarity criterion by taking advantage of the rule that mutual information is largest at spatial position consistent to achieve the best parameters to improve the accuracy. Experiment results showed that with regard to the 2048 pixel *2048 pixel image, the registration method in this paper can achieve pixel level accuracy in registration translation amount, not more than 0.1 degrees in registration angle, less than 2.1 seconds in registration time, which meeting the actual large quantities of parts registration requirement.

image registration;smallest minimum bounding rectangle;centroid; mutual information

TH164

A

10.19287/j.cnki.1005-2402.2016.07.026

苏森，男，1989年生，硕士，工程师，研究方向为机器视觉、图形图像。

2016-02-02)

160735