基于Lagrange方法的单旋翼飞行器动力学建模

李家乐, 王正平

(西北工业大学 航空学院, 陕西 西安 710072)



基于Lagrange方法的单旋翼飞行器动力学建模

李家乐, 王正平

(西北工业大学 航空学院, 陕西 西安 710072)

为了进行微小型单旋翼飞行器的动力学建模,通过建立多个坐标系来反映各部分间的相对运动。首先,利用坐标变换得到位置、速度及加速度等向量,并代入拉格朗日方程得到运动学模型;然后,对模型进行数值求解,得到飞行器的姿态响应。仿真结果表明,飞行器定点盘旋时合外力为零,能量保持不变;爬升或前飞时有非保守力做正功,能量增大。

Lagrange方程; 坐标变换矩阵; 传输定理; 稳定性分析

0　引言

对于微小型飞行器SAMARAI[1]的构形,目前已有稳定性分析[2]、翼型分析[3]以及运动的数值仿真结果[1]，但是缺失了很重要的一部分,即如何推导运动学方程。

对于常规布局飞机,通常应用飞行力学中的六自由度方程等方法进行动力学建模和分析。本文将不采用六自由度方程来建立模型,而是采用Lagrange方程法,该方法能够很好地仿真机体各部分间有相对转动的飞行器。通过对机体不同部分建立不同的坐标系,分析坐标系间的变换矩阵和相对转动角速度。利用动能和势能表示出拉格朗日算子，并带入拉格朗日方程从而得到运动学方程。

本文按照该系统化的过程,分析了飞行器运动的特点和稳定性,进而简化了模型和推导过程。关键在于利用传输定理将速度、加速度变换至同一坐标系下。最后编写Matlab程序数值求解方程,得到不同输入下的响应。该模型能够实现飞行器的定点盘旋、爬升和前飞状态的仿真,并且从能量的角度能够验证建模、仿真的正确性。

1　外形尺寸、重量及坐标系的建立

微小型飞行器SAMARAI的外形如图1所示,简化结构及外形尺寸如图2所示。

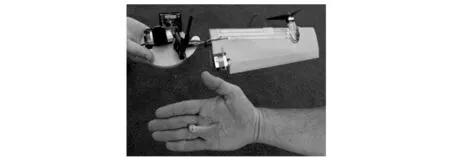
图1　SAMARAI 外形图Fig.1　The layout of SAMARAI

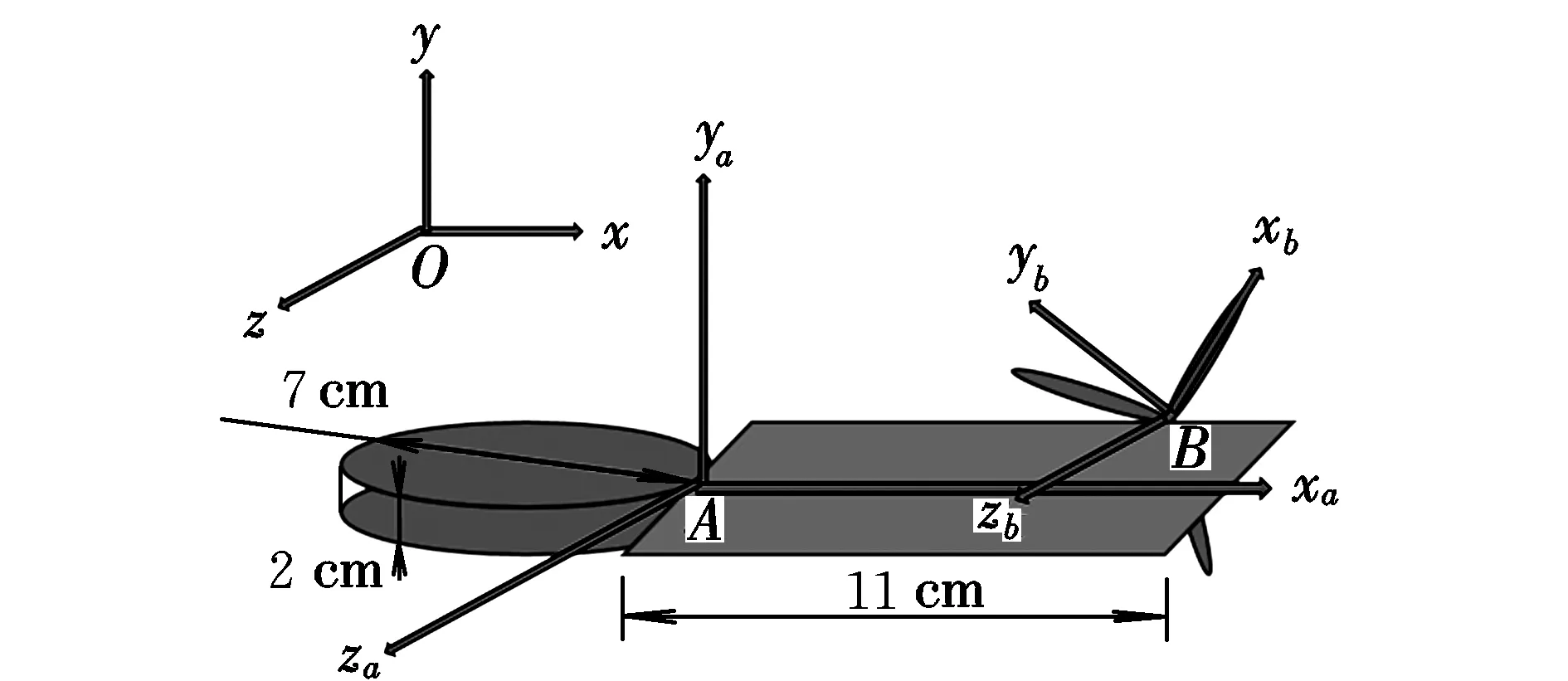
图2　构形、坐标系及尺寸Fig.2　Configuration, coordinate systems and dimensions

该飞行器由一个直径为7 cm、高度为2 cm的航电盘,展长为11 cm的机翼,以及1个拉力螺旋桨组成。前两者分别记为B1和B2,整个机体记为B。机翼翼型为AG38[3],认为该机翼上并无展向流动,在4°迎角时,机翼的升力系数、阻力系数约为0.7和0.04。

对于同样尺寸的单翼飞行器,质量可以小于0.075 kg,旋转速度可达80.5 rad/s。假设飞行器总重0.06 kg,航电盘质量m1为0.037 kg,剩余部分质量m2为0.023 kg。调整内部部件的分布可保证飞行器的重心在盘和机翼相交处。

SAMARAI为一个被动的稳定系统,通过定性的稳定性分析可知,SAMARAI能够做到在平面内旋转[2],这样可简化坐标系的建立。

Oxyz坐标系为地面坐标系;Axayaza坐标系的原点A在飞行器重心处,随着航电盘一起运动,由Oxyz坐标系绕Oy轴旋转角度φ得到;Bxbybzb坐标系的原点B在机翼重心处,随机翼一起运动,由Axayaza坐标系绕Axa轴旋转角度α得到,反映了机翼的迎角;Cxcyczc坐标系的原点C在拉力螺旋桨重心处,由Bxbybzb坐标系绕Bzb轴旋转角度θ得到。

2　动力学分析

2.1坐标系间的变换矩阵

由于机体各部分间有相对转动,需要坐标变换矩阵来实现同一向量在不同坐标系下的坐标转换。由上文可知,将Oxyz坐标系绕Oy轴旋转角度φ得到Axayaza坐标系,则从坐标系Oxyz到Axayaza的坐标变换矩阵CAO为:

(1)

式中:cφ,sφ分别表示cosφ和sinφ。

同理便可以得到坐标变换矩阵:

又因为连续的坐标变化可以通过左乘一系列的坐标变换矩阵得到,所以:

(2)

综上所述，CAO可将向量在Oxyz坐标系下的坐标变换至Axayaza。同理可得CCO为:

坐标系间相对转动角速度为:

(3)

2.2质点的运动学向量

认为p是机翼上一质点,q是螺旋桨尖上一质点,它们在各坐标系中的位置为:

(4)

质点p和q相对于地面的速度即为位置向量在地面坐标系下的导数,可以将位置向量写为两个向量之和,再进行求导,分别为:

(5)

(6)

加速度为:

(7)

3　动力学模型及拉格朗日方程

3.1动力学模型

拉格朗日方程将所有非保守力纳入计算中,重力、升力、阻力及推力分别为:

G=[0-mBg0]FA

(8)

=[-LsαsφLcαLsαcφ]FO

(9)

=[DcαsφDsαDcαcφ]FO

(10)

式中:L为升力;CL为机翼的升力系数;CD为阻力系数;c为机翼的弦长;b为机翼展长;ds为翼段展向微元。

假设推力的大小为T,始终指向-zc方向,有:

(11)

如果推力和阻力平衡,则转动角速度为64.37 rad/s。

分别将航电盘和剩余部分的重心记为C1和C2,则:

(12)

(13)

式中:d1和d2分别为B1和B2的重心到坐标系Axayaza原点A的x向距离。

惯性静矩I、转动惯量J分别为:

(14)

(15)

可以验证,整个飞行器的转动惯量满足稳定性的要求[4]。

3.2建立拉格朗日运动方程

定义系统广义坐标为q=[xb,yb,zb,ε]T,从而广义坐标及其时间导数能够完全描述飞行器的运动状态。B1的动能为:

式中:V为速度;dm1为航电盘质量微元。将式(3)和式(6)带入上式,并写作矩阵形式为:

(16)

B2的动能为:

(17)

机体的总动能和总势能为:

(18)

(19)

将拉格朗日算子定义为:

(20)

考虑功、虚功、广义力和广义力矩,虚功、虚位移分别为δW和δr,虚功为力通过虚位移作用在刚体上的功,所以有:

(21)

带入无约束的拉格朗日方程:

(22)

于是方程变为:

(23)

式中：f[q(t)]中的分项为广义力和广义力矩,与升力、阻力和推力相关。将迎角和推力认为是两个输入[5],改变输入,能实现不同的运动。

4　数值仿真及结果分析

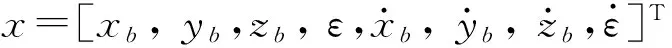
4.14°迎角下的稳定盘旋

从直观角度来看,稳定盘旋意味着机体受力平衡,f[q(t)]=0,能够求解出转动角速度为64.37 rad/s。迎角和推力两个输入都不发生变化,如果模型正确,能量应该保持不变。飞行器在4°迎角下的稳定盘旋时的状态如图3所示。

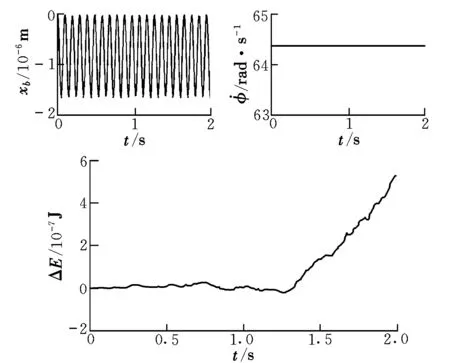
图3　稳定盘旋时的状态和能量变化Fig.3　Variation of states and energy in steady hover

由图3可知,飞行器的位置和自转角速度基本保持不变,表示飞行器能够在空中某一位置稳定盘旋。能量基本不变,说明只有保守力做功,符合实际情况,验证了数值仿真的正确性。

4.2爬升和前飞

保持推力不变,迎角随转动角速度变化从而实现爬升和前飞。在这种情况下,推力对飞行器做功,能量应不断增大。计算虚功为:

(24)

仿真结果如图4所示。由图4可以看出,x基本不变;y正向增大,表示飞行器爬升;z负向增大,表示飞行器前飞。能量的不断增大是由于非保守力做功。仿真结果符合前文的理论分析结果。

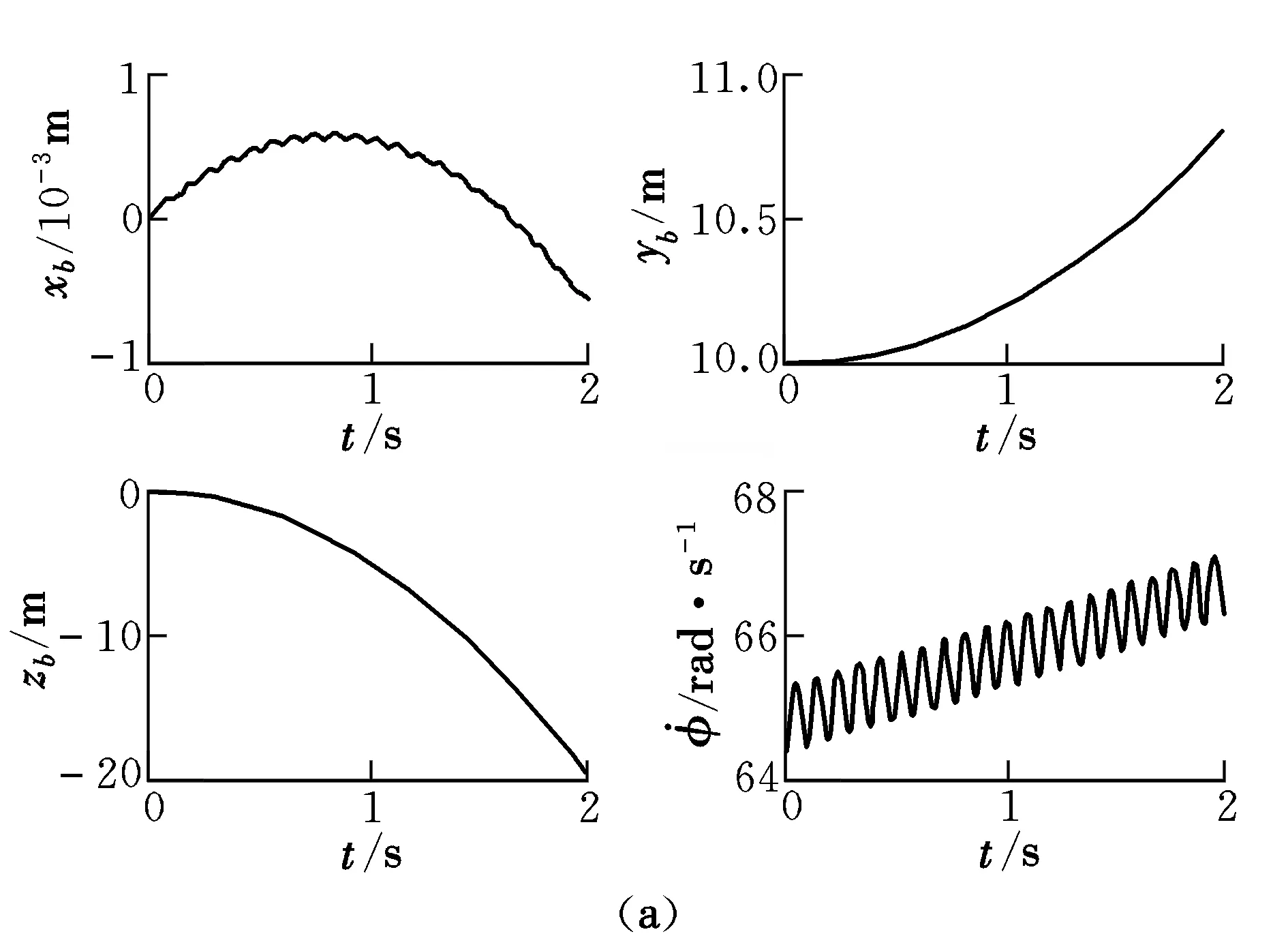
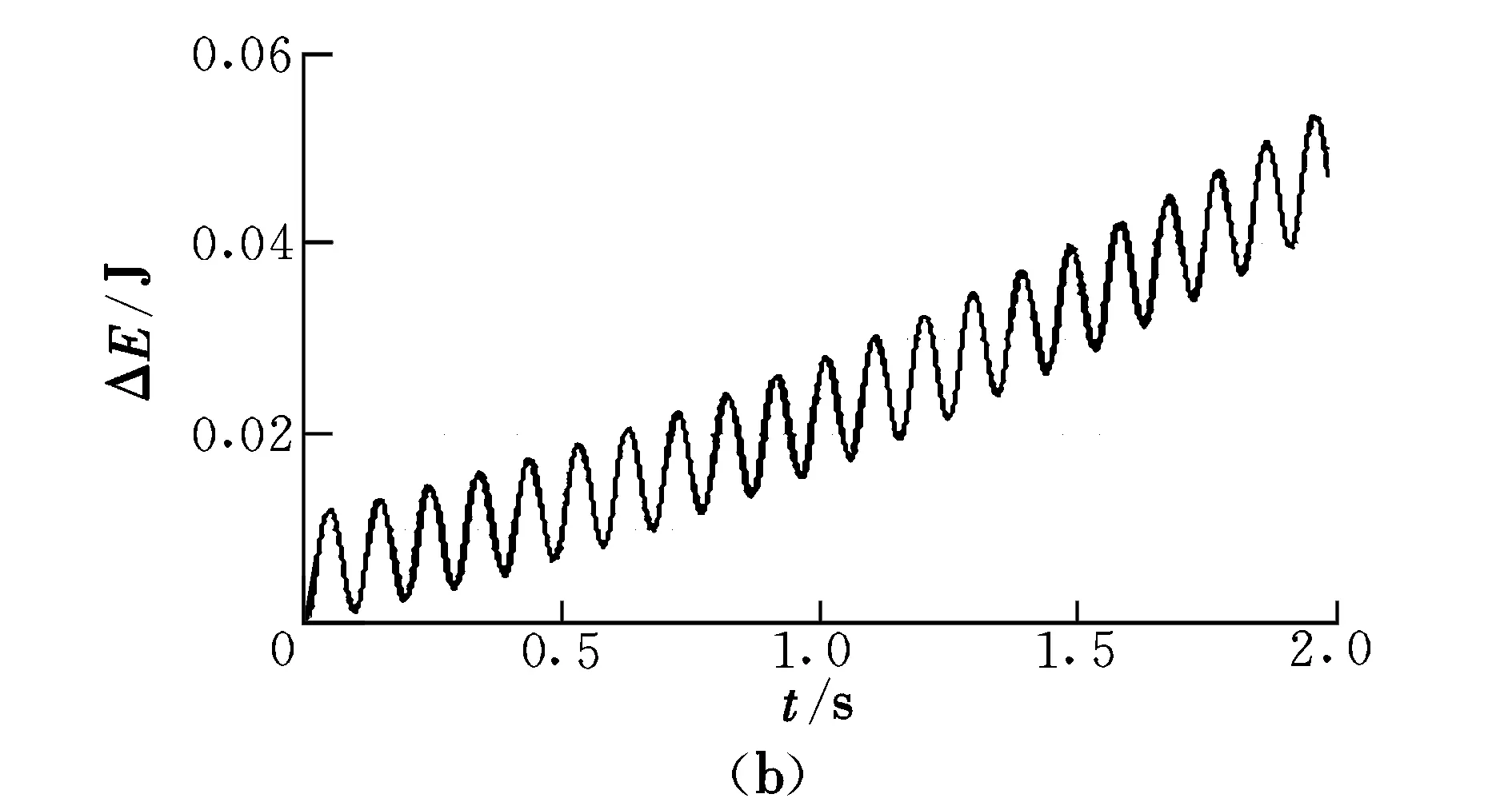
图4　爬升和前飞时的状态和能量变化Fig.4　Variation of state and energy in climbing and flying forward

5　结束语

针对单旋翼飞行器,利用Lagrange方法能够比较容易地推导出运动模型,而且推导过程系统化,容易准确实现。本文方法可以推广到其他飞行器,如四旋翼飞行器等;对于柔性体,可以将飞行器看作多个质点,对拉格朗日算子求和,同样具有实用性;对于更为复杂的运动体系,可以将体系看作几个相互约束的部分。这些将作为下一步研究的内容。

[1]Jameson S,Fregene K,Chang M,et al.Lockheed martin’s SAMARAI nano air vehicle:challenges,research,and realization[R].AIAA-2012-0584,2012.

[2]Ulrich E R,Humbert J S,Pines D J.Pitch and heave control of robotic samara micro air vehicles[J].Journal of Aircraft,2010,47(4):1290-1299.

[3]Youngren H,Kroninger C,Chang M,et al.Low reynolds number testing of the AG38 airfoil for the SAMARAI nano air vehicle[R].AIAA-2008-417,2008.

[4]Youngren H,Jameson S,Satterfield B.Design of the SAMARAI monowing rotorcraft nano air vehicle[C]∥Proceedings of the American Helicopter Society AHS 65th Annual Forum and Technology Display.Fort Worth,Texas:Americom Helicopter Society,Inc,2009.

[5]Fregene K,Bolden C L.Dynamics and control of a biomimetic single-wing nano air vehicle[C]∥American Control Conference (ACC),2010.Baltimore,MD:IEEE,2010:51-56.

(编辑：李怡)

Dynamics modeling for monowing rotorcraft using Lagrange method

LI Jia-le, WANG Zheng-ping

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

For the dynamics modeling for the microminiature monowing rotorcraft, several coordinate systems for different parts of the vehicle were set up to reflect the relative movements. Firstly, vectors such as position, velocity and acceleration were obtained by transformation of coordinates, and substituted into Lagrange equation to get dynamic model. Then, attitude responses were obtained by numerical calculation of the model. Simulation results show that the force is zero and the energy remains constant when the rotorcraft is hovering; non-conservative force works and the energy increase when the rotorcraft is climbing or flying forward.

Lagrange equation; direction cosine matrix; transport theorem; stability analysis

2015-08-24;

2016-02-20; 网络出版时间:2016-02-29 16:37

李家乐(1991-)，女，陕西渭南人，硕士研究生，研究方向为飞行器动力学和控制；

王正平(1964-)，男，陕西西安人，教授，研究方向为飞行器设计。

V212; V275.1

A

1002-0853(2016)04-0015-04