多面体网格在静气动弹性计算中的应用

冯浩洋, 苏新兵, 马斌麟, 王旭

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



多面体网格在静气动弹性计算中的应用

冯浩洋, 苏新兵, 马斌麟, 王旭

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

介绍了多面体网格技术在静气动弹性问题中的应用。基于M6算例和径向基函数插值法,探究了多面体网格的CFD计算效率和变形能力,使用AGARD445.6机翼进行了静气动弹性数值计算。结果表明,多面体网格具有计算效率高、变形能力强、计算结果准确等优点,可适用于静气动弹性问题的数值计算。

多面体网格; 静气动弹性计算; 网格效率; 网格变形

0　引言

随着计算机性能的提高和相关学科的发展,基于计算流体力学(CFD)和计算结构力学(CSD)的流固耦合仿真技术逐渐应用于气动弹性数值模拟。在流固耦合仿真中,CFD计算占用了90%以上的时间,而且伴随CSD的求解,CFD网格会产生变形。因此,CFD网格的计算效率和变形能力是仿真快速、准确的关键。当前,CFD网格主要有四面体、六面体(切割体)和多面体三种类型。四面体网格对模型的自适应性好,变形能力强,但是计算量大,容易产生伪耗散。切割体网格生成质量高,计算量小,但变形能力弱[1]。多面体网格作为近年来新兴的一种网格技术,具有生成方便快捷,对复杂外形具有良好的适应能力等特点,得益于其独特的网格架构和有更多的相邻单元,数值模拟可以快速地收敛,梯度的计算和当地的流动状况预测更准确。由于多面体对几何的变形没有四面体敏感,因此多面体网格可以更好地保证变形后的网格质量[2-3]。

本文对四面体、切割体、多面体网格的计算效率进行了比较,检验了多面体网格的变形能力。在文献[4]方法的基础上,基于多面体网格和径向基函数的网格变形方法,通过AGARD算例,对机翼的静气动弹性现象进行了仿真,验证了多面体网格的有效性。

1　网格计算效率

为了探究多面体网格的计算效率,本文分别采用四面体、切割体、多面体网格对M6机翼算例进行了计算和对比。在文献[2]中,已经对网格总数不一致的情况进行了讨论,并得出了多面体网格收敛速度快、计算精度高的结论。本文进一步对基于相同网格单元数的情况进行了探讨。在调整面网格尺寸并进行网格独立性验证后,可知三种网格数量在1 900 000左右可以满足算例要求。剖分后的网格单元数量如下:四面体网格单元数目为1 984 521,切割体网格单元数目为1 948 756,多面体网格单元数目为1 956 546。剖分后的翼根前缘网格如图1所示。

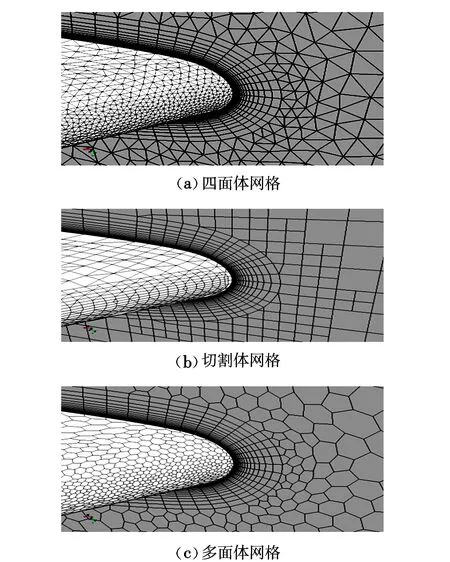
图1　翼根前缘网格示意图Fig.1　The mesh of wing root leading edge

取N-S方程作为流场数值求解方程。空间离散采用中心差分格式,湍流模型为S-A模型,采用耦合隐式方法进行求解。为了加速收敛,在不影响计算精度的前提下,设置库朗数为50,松弛因子为0.5。计算状态为:Ma=0.839 5;Re=11.72×106;α=3.06°。经计算,得到如图2所示的三种网格的机翼沿不同展向的压力分布数值模拟计算结果与实验数据[5]的对比。

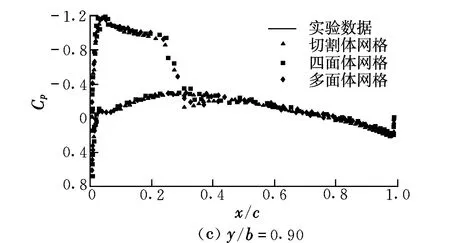
图2　翼展不同站位的压力系数分布Fig.2　Pressure coefficient distributions at different wingspan positions

由图2可知,三种网格在计算准确性上几乎没有差别,切割体网格在y/b=0.65处对前缘激波的模拟较另两种网格差,这可能是由于其贴体性较差,在曲率较大的地方难以与几何外形精确吻合导致的。

三种网格下的计算残差曲线如图3所示。由图3可以看到,三者的收敛速度大致相同,多面体网格和四面体网格在150步左右收敛,切割体网格在180步左右收敛。四面体网格收敛速度快是因为其节点数最少,易于收敛,但其收敛精度最低。多面体网格在与四面体网格收敛速度相当的同时,收敛精度远比其高,与切割体网格大致相同,但多面体网格收敛过程更加平稳。

图3　残差收敛曲线Fig.3　The residual convergence curves

三种网格的收敛精度和计算时间如表1所示。由于切割体网格在计算过程中耗散最小,且M6机翼外形简单,因此其所用时间最短,而多面体网格计算时间小于四面体网格。

表1　收敛精度和计算时间Table1　Convergenceaccuracyandcomputationtime

由计算结果可知,多面体网格在流体计算过程中综合了四面体网格和切割体网格的优点。当网格数相同时,多面体网格在收敛速度快的同时还有较高的精度和平稳度。因此,相较于切割体网格和四面体网格,采用多面体网格进行静气动弹性计算可以提高CFD的计算效率和准确性,从而缩短整体计算时间。

2　网格变形能力

为了检验多面体网格的变形能力[6],本文基于径向基函数变形方法[7-10],对M6机翼的网格进行了旋转变形,并对变形前后机翼的气动参数进行了计算和对比。

采用上文所剖分的多面体网格,以翼根前缘顶点为圆心,z轴为转轴,对机翼进行45°旋转。为便于观察,取流场的对称面网格旋转变形,如图4所示。对于航空外流问题,计算结果的准确性与边界层的质量息息相关,因此本文着重对边界层网格的变形质量进行分析。为了更好地显示变形细节,对变形前后翼根的前后缘(黑框内部分)进行局部放大,放大后的网格如图5所示。

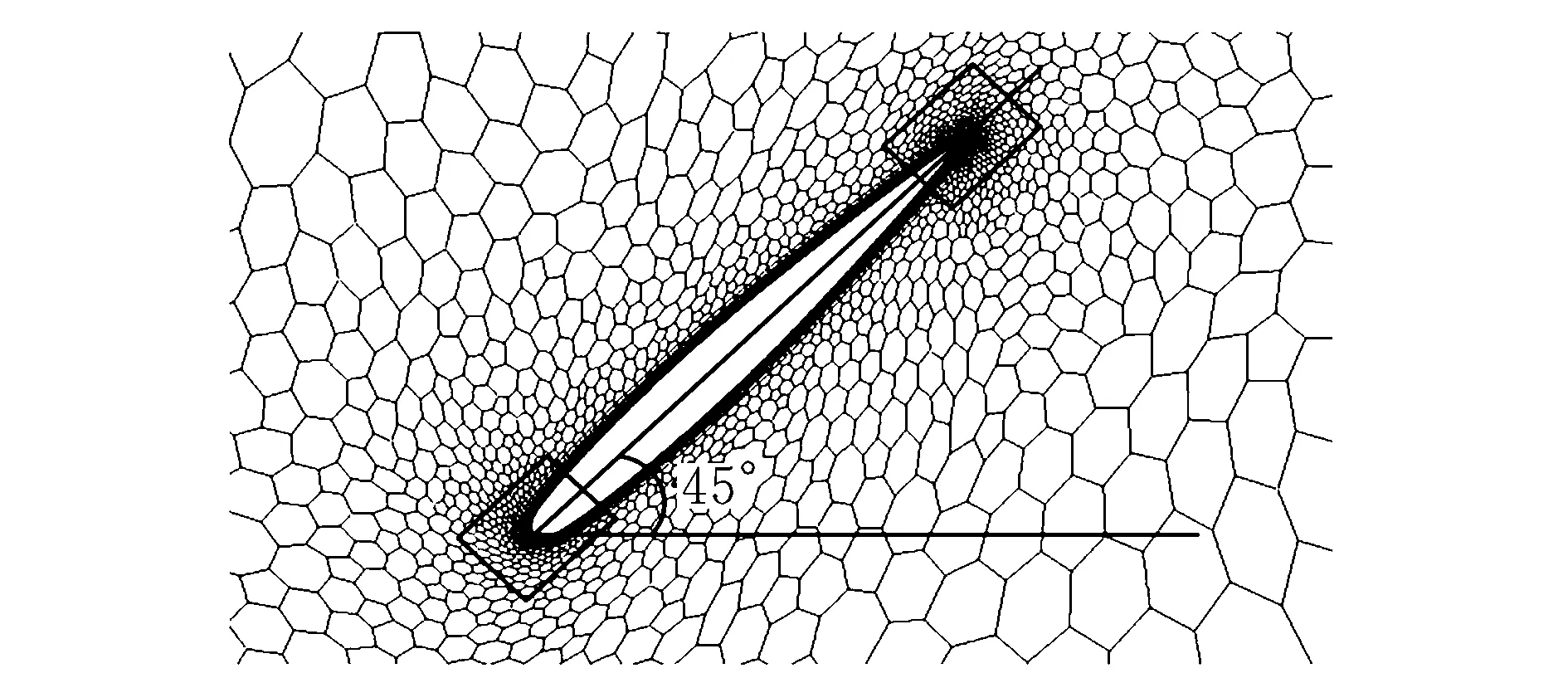
图4　机翼旋转示意图Fig.4　The wing rotation diagram

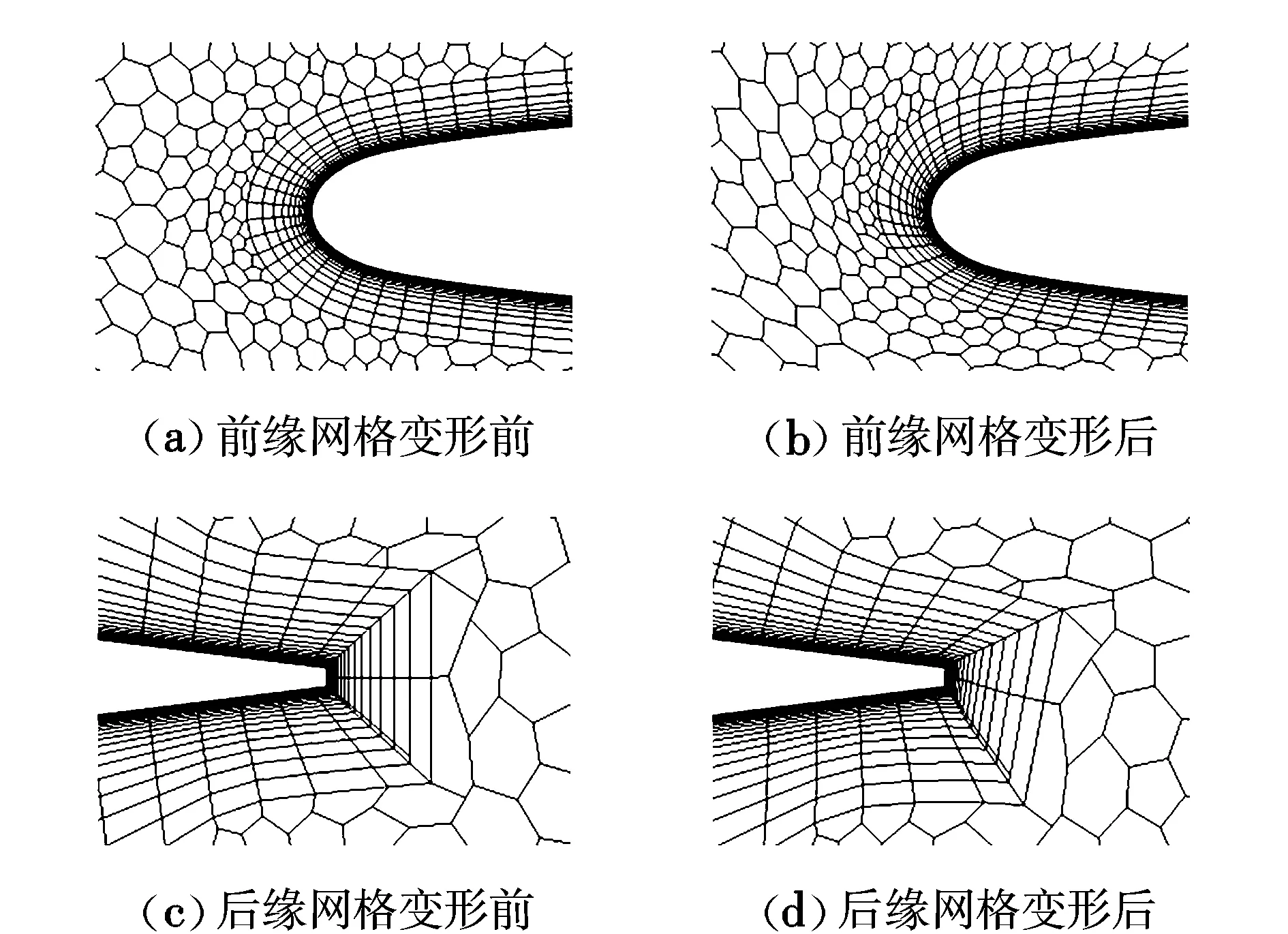
图5　翼根切面前后缘网格变形比较Fig.5　Comparison of mesh deformation at wing root section leading and trailing edge

由图可见,在机翼旋转变形45°的情况下,其前后缘网格都发生了不同程度的偏斜。后缘偏斜程度较大,这是因为后缘尺寸较小,其边界层网格的外边界与后缘壁面的距离相对较远所致。基于径向基函数的变形方法对远离壁面网格节点的控制力较弱,在大变形情况下,网格经过多次迭代变形会产生较大的误差,导致后缘处网格偏斜更为严重。

对于航空外流问题,近壁面第一层网格高度应当满足湍流模型的计算要求,本文选取的是S-A模型。为了提高升力、阻力计算结果的准确程度,需要求解粘性子层,这就要保证壁面Y+值小于1[11]。取机翼y/b=0.5处的截面,在变形前后对其壁面Y+值进行计算,结果如图6所示。由图6可以看到,该截面的Y+值几乎没有发生变化,只有后缘处变化幅度相对较大,这也与网格变形情况相符。图中变形前后的Y+值均在(0,1)区间内,满足湍流模型的计算要求。

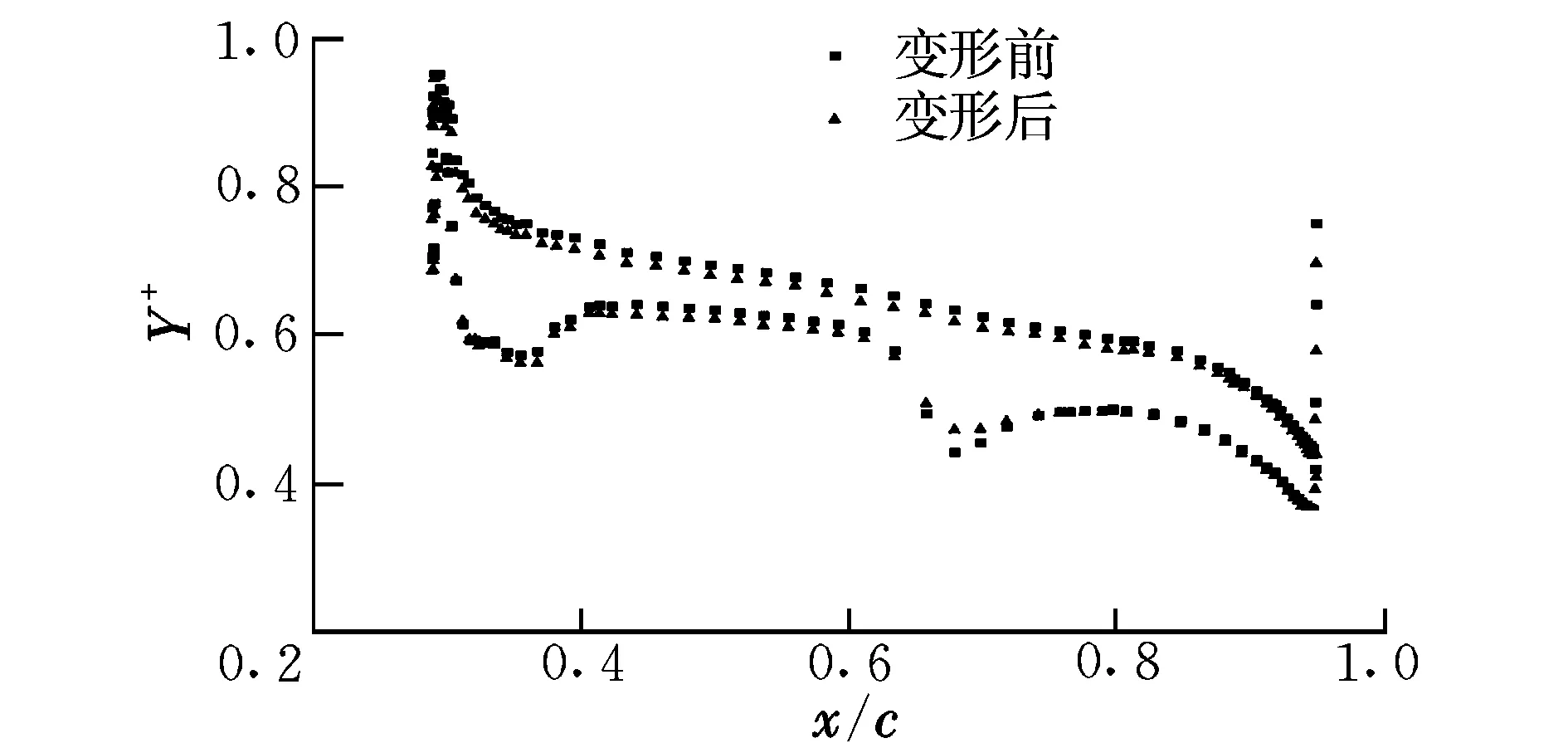
图6　y/b=0.5处Y+值变化Fig.6　The change of Y+value on y/b=0.5

依照上节边界条件对变形后的流场网格进行计算,得到如图7所示的变形前后机翼沿不同展向的压力分布。由图7可知,尽管前缘和后缘处的网格发生了偏斜,但是计算结果仍然是准确的,可以认为局部网格的偏斜对计算没有造成负面影响。

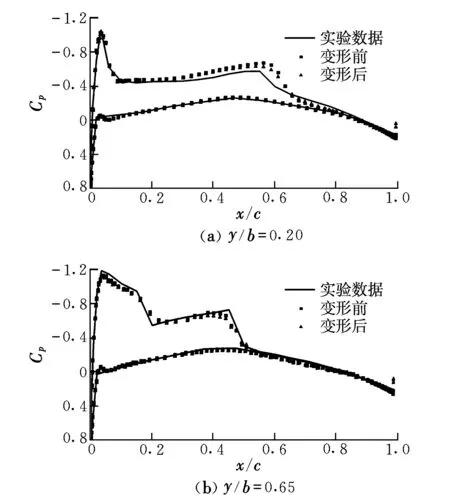
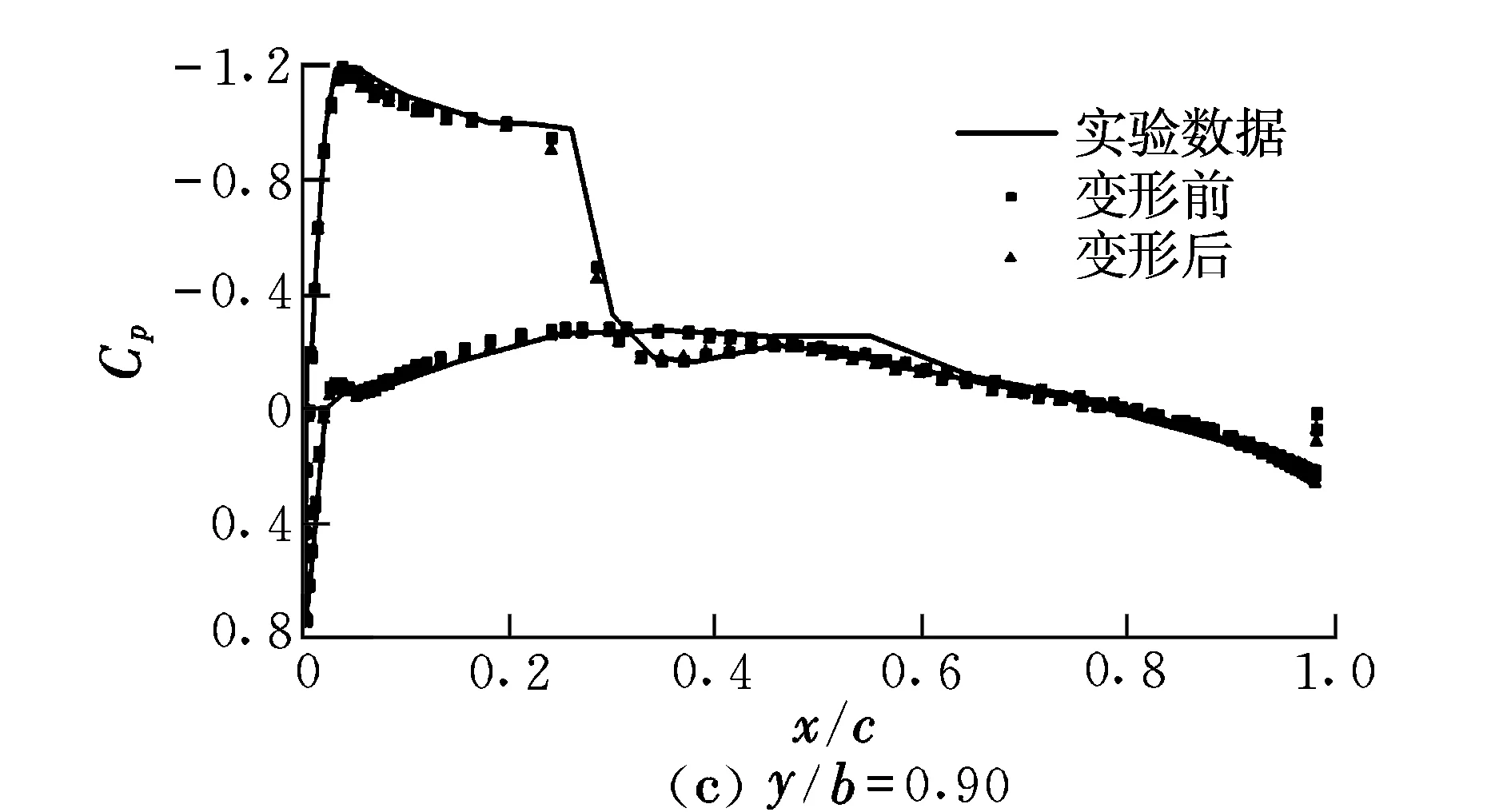
图7　变形前后翼展不同站位的压力系数分布Fig.7　Pressure coefficient distributions at different wingspan positions before and after deformation

网格变形前后的收敛曲线如图8所示。由图8可知,曲线都在260步左右达到收敛;但是变形后网格计算结果的收敛曲线不如变形前平稳,而且收敛精度比变形前略差。这是因为变形后的网格整体质量有所下降,致使计算过程中出现伪耗散,使得收敛精度降低。尽管如此,由于计算结果的准确性并没有受到影响,所以仍然说明多面体网格在该变形方法产生大变形后可以满足计算要求。

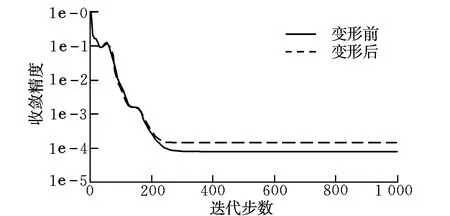
图8　变形前后残差收敛曲线Fig.8　The residual convergence curves before and after deformation

3　流体、结构计算和数据传递方法

静气动弹性变形是由飞行器外部载荷与机体弹性结构相互耦合作用产生的,需要耦合气动力方程和结构静平衡方程进行求解。流体求解模型与上文相同,由于计算的是静气动弹性问题,所以不需要在时域上进行求解。为了提高效率,对流体进行稳态求解。结构求解采用柔度矩阵法,流体和结构之间用松耦合的方式进行数据交换,采用无限平板插值方法(IPS)完成两者之间的数据传递[4,12]。

4　算例验证

采用标准的AGARD445.6机翼对本文的气动弹性计算方法进行验证。AGARD机翼为NACA65A004翼型,展弦比为1.65,梢根比为0.66,展长为0.76 m,根弦长为0.56 m,弦线后掠角为45°[13]。剖分的流体网格和结构网格如图9所示,流体网格数为2 401 689,结构网格数为9 593。

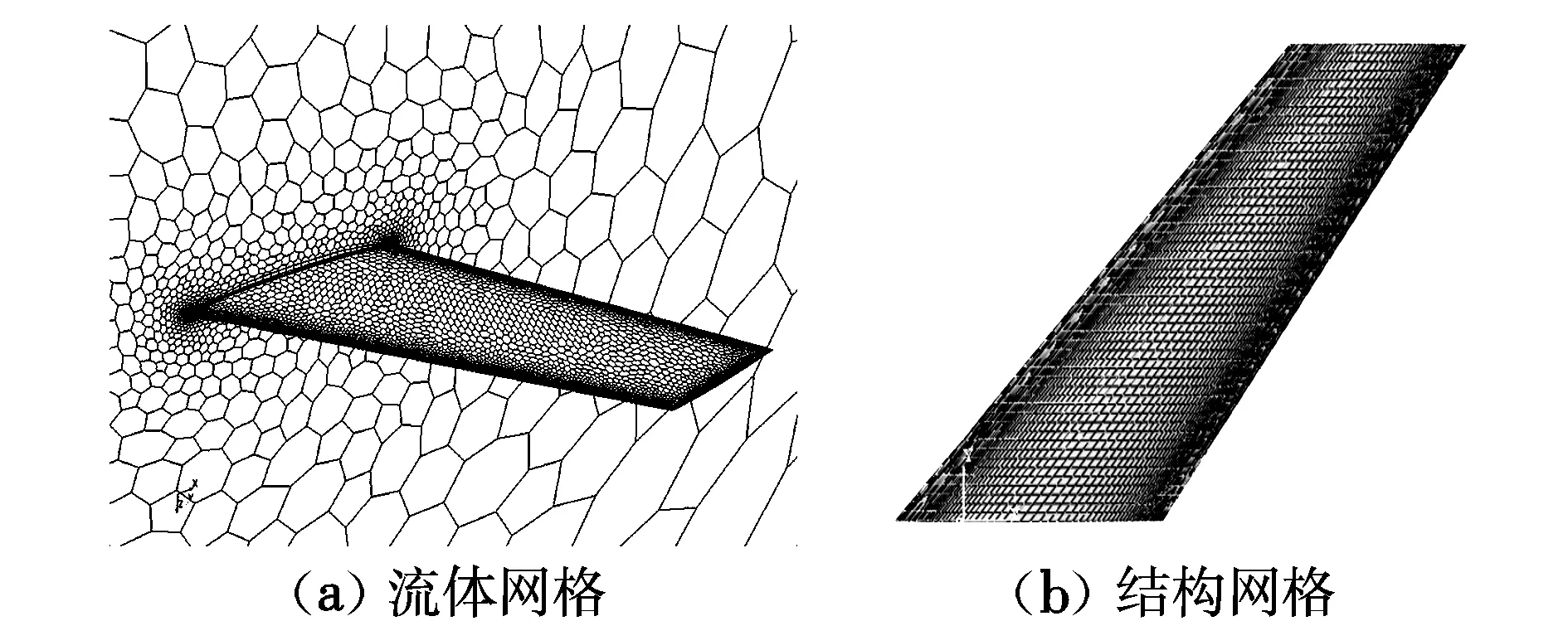
图9　AGARD机翼流体网格和结构网格Fig.9　The fluid mesh and structure mesh of AGARD wing

根据文献[12],设置结构材料属性为:E1=0.89 GPa,E2=1.54 GPa,ν=0.31,G=2.6 GPa,ρ=381.98 kg/m3。其中,E1为材料x和z方向的弹性模量;E2为y方向的弹性模量(x沿弦向,y沿展向);ν为泊松比;G为每个方向的剪切模量;ρ为机翼模型的密度。

计算状态选择Ma=0.8,α=1°。AGARD 445.6机翼静气动弹性迭代平衡后,相对于初始位置,翼梢前缘和后缘的变形量如表2所示。由表2可以看出,本文方法与文献[14] 的计算结果基本一致。变形量有误差是由于插值方法的限制和网格数量的不同,数据在传递过程中会有一定的偏差所致。由于结果相差都在3%以内,所以这样的误差是可以接受的。

表2　AGARD 445.6机翼静气动弹性结果比较Table2　ComparisonofAGARD445.6wingstaticaero-elasticcomputationalresults

5　结束语

基于多面体网格,本文对静气动弹性计算的效率和网格变形问题进行了如下三方面的探究:

(1)在流场数值模拟的基础上,对切割体、四面体和多面体网格的计算效率进行了对比。M6机翼计算结果表明,在基于相同单元数的情况下,多面体网格相比另外两种网格可以极大地缩短流体计算的时间。由于多面体网格能以更少的网格单元数量划分流场,因此,在实际计算过程中多面体网格拥有比本文所给数据更大的效率优势。

(2)基于径向基函数的网格变形方法,本文对多面体网格的大变形能力进行了检验。结果表明,变形后整体网格质量的下降导致了收敛精度的降低,但是边界层网格的质量变化不大,可以保证计算结果的准确性。

(3)基于多面体网格对AGARD算例进行了验证。计算结果表明,多面体网格可以对机翼的静气动弹性问题进行较为准确的仿真。

由于目前还没有合适的方法对多面体网格的变形质量进行评价,因此本文只对网格变形前后的流场计算结果进行了比较,并由此判定网格变形质量满足计算要求,并没有对网格质量的变化进行精确的量化。如何对网格变形前后的质量进行量化和比较,从而在切割体、四面体和多面体网格中找到变形能力最强的网格以及各自适宜的变形方式是今后需要做的工作。

[1]王明强,朱永梅,刘文欣.有限元网格划分方法应用研究[J].机械设计与制造,2004,2(1):22-24.

[2]李海峰,吴冀川,刘建波,等.有限元网格质量剖分与网格质量判定指标[J].中国机械工程,2012,23(3):368-377.

[3]许晓平,周洲.多面体网格在CFD中的应用[J].飞行力学,2009,27(6):87-89.

[4]陈大伟,杨国伟.静气动弹性计算方法研究[J].力学学报,2009,41(4):469-479.

[5]Schmitt V,Charpin F. Pressure distributions on the ONERA-M6-Wing at transonic Mach numbers,experimental data base for computer program assessment[R].France:Report of the Fluid Dynamics Panel Working Group 04,AGARD AR 138,1979.

[6]张伟伟,高传强,叶正寅.气动弹性计算中网格变形方法研究进展[J].航空学报,2014,35(2):303-319.

[7]Hardy R L.Theory and applications of the multiquadric-biharmonic method[J].Computers & Mathematics with Applications,1990,19(8-9):163-208.

[8]Faul A C,Goodsell G,Powell M J D.A Krylov subspace algorithm for multiquadric interpolation in many dimensions[J].IMA Journal of Numerical Analysis,2005,25(1):1-24.

[9]Gumerov N A,Duraiswami R.Fast radial basis function interpolation via preconditioned Krylov iteration[J].SIAM Journal on Scientific Computing,2010,29(5):1876-1899.

[10]Beatson R K,Powell M J D,Tan A M.Fast evaluation of polyharmonic splines in three dimensions[J].IMA Journal of Numerical Analysis,2006,27(3):427-450.

[11]胡坤,李振北.ANSYS ICEM CFD工程实例详解[M].北京:人民邮电出版社,2014:210-215.

[12]卢学成,叶正寅,张陈安.基于ANSYS/CFX耦合的机翼颤振分析[J].计算机仿真,2010,27(9):88-91.

[13]Yates E C Jr.AGARD standard aeroelastic configurations for dynamic response Ⅰ:wing 445.6 [R].NASA TM-100492,1987.

[14]Cai J,Liu F.Static aero-elastic computation with a coupled CFD and CSD method[R].AIAA-2000-0717,2000.

(编辑：姚妙慧)

Application of polyhedron grid in static aero-elastic computation

FENG Hao-yang, SU Xin-bing, MA Bin-lin, WANG Xu

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

The static aero-elastic computation with polyhedron grid was introduced. The CFD computational efficiency and deformation ability of polyhedron grid were studied based on M6 numerical example and interpolation method of radial basis function. The static aero-elastic numerical value was calculated with the use of AGARD 445.6 wing. The results show that the polyhedron grid possesses the advantages of computational efficiency, deformation ability and accurate calculation results, so it is suitable to the static aero-elastic computation.

polyhedron grid; static aero-elastic computation; grid efficiency; grid deformation

2015-10-21;

2016-03-14; 网络出版时间:2016-04-22 09:52

冯浩洋(1991-)，男，河北高邑人，硕士研究生，研究方向为前掠翼飞机的静气动弹性现象及规律。

V211.3

A

1002-0853(2016)04-0024-05