利用多准则Hopfield网络对ECT进行图像重建

吴新杰，　何在刚，　李惠强，　郑静娜，　陈玲，　许超，　陈跃宁，　颜华

(1. 辽宁大学 物理学院，辽宁 沈阳 110036；2. 沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870)



利用多准则Hopfield网络对ECT进行图像重建

吴新杰1，何在刚1，李惠强1，郑静娜1，陈玲1，许超1，陈跃宁1，颜华2

(1. 辽宁大学 物理学院，辽宁 沈阳 110036；2. 沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870)

针对电容层析成像技术中图像重建质量较差的问题，提出一种基于多准则Hopfield网络模型的电容层析成像的改进图像重建算法。首先分析了ECT图像重建和Hopfield网络的基本原理，然后根据ECT图像重建的特点确定了4种准则函数：图像熵、测量电容和估计电容的误差平方和、重建图像的局部非均匀性函数和总变差，并将这4种准则函数引入Hopfield网络的能量函数中，由此推导出Hopfield网络的动态方程，在此基础上得到ECT图像重建迭代算法，最后通过仿真实验对所提方法进行了验证。仿真实验结果表明利用此方法获得的重建图像误差和相关系数比LBP算法和Landweber迭代算法得到的相应指标要好。由此可见，该方法是一种有效的、精确度较高的ECT图像重建方法。

电容层析成像；图像重建；Hopfield网络；多准则；图像误差

0　引　言

随着科技的迅速发展，在生产环境越来越复杂的情况下，两相流、多相流在化工、环保、冶金、医疗和石油等国民生产领域中的使用越来越广泛。但是由于两相流、多相流的流型复杂、流动多变、流动过程有很大的随机性，采用传统的检测技术难以准确测量。电容层析成像技术(electrical capacitance tomography,ECT) 是20世纪80年代后期形成和发展起来的一种新型层析成像技术[1-2]，由于其具有非侵入、响应快、低成本等优点，在国内外现已成为人们关注的焦点。

ECT图像重建算法的优劣直接影响到传感器内部介电常数的分布和可视化效果[3]。ECT图像重建是一个典型的病态问题，它的解很不稳定，输入的测量数据若有微小的误差波动可能会使重建的图像产生较大的波动。不同的算法已被发展用于ECT图像重建，目前ECT图像重建算法大致分为直接算法、迭代法和其他算法。直接算法主要有线性反投影(linear back projection, LBP)算法[4]、奇异值分解(singular value decomposition,SVD)方法[5]和 Tikhonov正则化方法[6]等，LBP算法结构简单、成像速度快，但其重建的图像精确度较低，适合于准确度要求不高的工业在线检测；SVD 方法的主要优点在于其广义逆最小模解可以较好地区分相邻的大小物体，不过其重建图像还会因为存在大量散斑而严重失真；Tikhonov正则化方法虽然能够得到近似稳定的图像重建效果，然而算法的解过于光滑，导致对介质边缘重建效果并不理想。迭代法比较有代表性的方法是Landweber算法[7-8]、Newton-Raphson算法[9]和同步迭代重建技术(Simultaneous Iterative Reconstruction Technique, SIRT)[10]等，Landweber算法成像质量优于一些其它算法，然而它是基于最速下降法的思想，沿着负梯度方向搜索最优解，容易收敛到局部极值，而且当参数设置不当时会导致结果发散；Newton-Raphson算法是求解无约束问题的最优化方法之一，在重建图像中具有更高的精确度，但在迭代方法中，灵敏度场STS病态严重，无法求得稳定的逆阵。SIRT算法也是最速下降算法的一种，它的原理和Landweber迭代算法是一样的，由于“软场”效应，精确度问题还有待提高。其他算法[11-14]主要有：模拟退火法、遗传算法、神经网络法及粒子滤波法等。

由于ECT图像重建问题是一个非线性的、病态的逆问题，而Hopfield网络提出了一种以神经元相互作用的一阶非线性微分方程组构成的神经网模型及其在能量函数极小化框架下的优化理论，可以映射任意复杂的非线性关系。因此，本文提出了一种基于多准则优化Hopfield网络的ECT图像重建算法。

1　电容层析成像系统基本原理

电容层析成像系统主要由3个部分组成：电容传感器、测量及数据采集和图像重建[15]。电容传感器获取被测物场分布状况的投影信息，测量及数据采集模块收集传感器所获得的信息，并传送至计算机，这些电容测量值反映了物场内介电常数的分布情况，计算机根据一定的图像算法重建出所研究管道截面的图像。

电容传感器不同电极组合间的电容值C和传感器内部介电常数分布ε(x,y)的关系表示为

(1)

式中：V是形成电容C的电极对之间的电势差，φ(x,y)为电势分布，Γ为电极边界。

以典型的8电极传感器系统为研究对象，可得到的独立电极对总数为

(2)

这样在8电极中总共可获得28个独立的测量数据。

目前，大多数ECT成像算法是基于介电常数分布到电容映射的线性模型，经过离散化、线性化和归一化后的模型如式(3)所示

C=S×G。

(3)

式中：C是m×1维的归一化电容测量向量；G是n×1维的归一化介电常数分布向量，在图像重建中代表图像灰度值；S是m×n的矩阵，反映了电容C受物质G分布变化的影响，称为敏感场灵敏系数矩阵。

ECT图像重建的目标就是在给定电容测量矩阵C后，快速地、有效地求解出在管道截面的介电常数分布G。该问题的求解在本质上属于病态问题，其解具有不适定性；因此为了获得有意义的数值解需要附加一定的约束条件。

2　基于多准则Hopfield网络的ECT图像重建算法工作原理

2.1HOPFIELD神经网络模型

Hopfield神经网络凭着其解决优化问题时呈现出容错性结构和结构上并行计算的优点，已经成功地应用于求解组合优化问题。

若一个组合优化问题的目标函数能够转化成Hopfield网络的能量函数，此时网络的每个神经元的状态就代表问题中的变量，这样就可以将组合优化的问题利用Hopfield网络来解决。也就是当网络的神经元趋于平衡点时，能量函数也趋近于最小值，目标函数优化计算的过程就是网络由初态向稳态收敛的过程。

由Hopfield神经网络原理可知，设神经元内部的状态函数vj为信号神经元输出电压，uj为vj的内部变量，它与vj之间的函数关系为vj=fΣ(uj)=(1+exp(-βuj)-1)。所以可得vj为单调递增函数，此处的β为增益的陡度，则以多目标优化准则为基础的神经网模型能量函数如式(4)所示[16]

(4)

式中：Rj是神经元的输入电阻，vj表示神经元的输出—输入非线性函数。第一项表示多目标函数的加权和，相当于代价函数；第二项是约束破坏的测度；第三项表示使神经网络工作在n维单位立体{0vj1}内部形成的系统状态空间。式(4)可以被看作是多目标优化准则为基础的神经网络的能量函数。

2.2多准则HOPFIELD网络的ECT图像重建

ECT系统在进行图像重建时，如果想要得到一个重建精确度高的图像，必须找到一个能够利用测量电容C映射出管道内的介电常数分布情况的方法，而且该方法可以有效地减小测量误差。显然，解决这一问题的关键是在已有的条件下，找到一个能够满足系统应用的折衷标准。根据ECT系统图像重建的基本过程及算法原理，电容C可以根据式(3)来计算。

因此在ECT系统的成像过程中，将灵敏度场、测量电容以及介电常数归一化后，通常就按照式(3)计算电极对间的电容值。如果ECT系统有8个极板，其重建图像的像素点数为20*20，则其对应的灵敏度场维数为28*400。

在很多工程与科学的优化问题中，往往存在多个性能准则函数。所以，利用多性能准则函数来解决复杂的优化问题，这样就更能够体现出问题的实质。

对于一个多目标函数的优化问题，问题中的函数之间往往相互矛盾，而且函数之间的数值范围以及量纲也不尽相同，由于这些因素的存在，导致在运用多目标函数优化的方法对问题进行优化求解时，最终得到的解对其中某一个目标函数来说可能不是最优解。在多目标函数优化问题上，向量目标函数的优化解一般使用非劣解(或称有效解)来描述。

通过多个准则函数来描述复杂的ECT重建图像，能够表现出ECT重建图像的多方面特性。第一个重建图像的目标函数的作用是得到最大图像熵；第二个函数是使测量电容和估计电容的误差平方和极小化；第三个函数的作用是保持图像的局部连续性和平滑性，为了达到这个目的采用了重建图像的局部非均匀函数极小化的方法；第四个目标函数是重建图像的总变差，目的是为了提高重建图像的分辨率。

第一个目标函数是重建图像的图像熵函数，其表达式为[17]

(5)

式中：N=400，即重建图像包含的像素点个数，γ1为归一化常数，且0γ11，Gj为重建图像的像素点j处的介电常数值，通过引入图像熵函数可以反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征。

第二个目标函数是电容传感器所测得电容值与估计出的电容值之间的方差，其数学表达式[17]为：

(6)

式中：M=28，即对应电容传感器测量获得的电容数量，γ2与γ1类似，是一个归一化常数，且0≤γ2≤1,通过使用该目标函数来确保重建图像的再投影数据和原始图像的投影数据尽可能接近。

第三个目标函数是图像的局部非均匀性函数，其表达式为[17]

(7)

式中：γ3是一个归一化常数，且0≤γ3≤1。X为非均匀矩阵，也称作平滑矩阵，维数为N×N，对于X矩阵内的元素，根据其对重建图像产生的作用，将其定义为[17]：

(8)

式中：x1，x2，x3表示的平滑矩阵中的权值，其值分别为1，-1/8，-1/8。在对重建出的图像进行平滑处理时，对图像上每个像素点j都要进行平滑处理，该像素点j位置的权值取为x1；与像素点j有一个公共边的相邻像素点为区域Ej，在进行平滑处理时权值取为x2；与该像素点有一 个公共点的相邻像素点为区域Vj，在进行平滑处理时，该区域的权值取为x3；其余的矩阵中的平滑权值对应的像素点由于和像素点j既没有公共点，又没用公共边，该区域权值取为0。然后利用目标函数f3(G)进行平滑处理。通过使用该目标函数，保持了图像的局部连续性和平滑性，同时，实现了重建图像的局部非均匀性函数和峰值性函数之和极小化。

第四个目标函数是重建图像的总变差，其表达式为[18]

(9)

式中：γ4为归一化常数，且0γ41，Li为对应灰度方差特性的稀疏矩阵；LiG对应不同区域的灰度方差。

根据上述四个目标函数，结合Hopfield神经网络模型，最终确定Hopfield神经网络模型的能量函数，ECT图像重建的Hopfield网络的能量函数表达式为

(10)

式中：N为Hopfield神经网络神经元的个数，即重建图像像素点的个数，Gj为相应的神经元的输出值，其物理意义为每个像素点位置处的介电常数值。

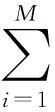
(11)

α(t)=α0+ζexp(-ηt)。

(12)

其中α0，ζ，η均为正数。由于Hopfield网络的能量函数是单调下降的，所以它往往会收敛于下降过程中的第一个极小值，但是这个极小值有时候并不是所需要的最优解，通过引入惩罚因子α，可以使能量函数在收敛时避免陷入局部极值。

(13)

式中：β、ξ分别为非线性函数线性部分的斜率和截距。在图像重建时，图像的最理想效果是当填充介质为气相时，该处介电常数为0，填充介质为固相时，该处的介电常数为1。用式(13)中的非线性函数来代替神经元使用的传统S型函数，取得的图像重建效果更好，所以选用以上函数来代替。

综上所述，将相应的目标函数代入到Hopfield网络的能量函数公式中，可得到基于多准则优化的Hopfield网络的能量函数

(14)

为了使运算简便，令式中的R0j=R0，C0j=C0，将R0C0，γ1/C0，γ2/C0、γ3/C0及γ4/C0分别用τ，γ1，γ2，γ3，γ4来代替。对能量函数的方程求导，可得到Hopfield网络的动态方程为：

lnG(t))+ω2γ2STZ(t)+

ω3γ3(XG(t)+G(t))+

ω4γ4H(t)-1J′(t)+STδ(Z(t))]。

(15)

，

(16)

G(t)=[G1(t),G2(t),…,GN(t)]T，

(17)

u(t)=[u1(t),u2(t),…,uN(t)]T，

(18)

z(t)=[z1(t),z2(t),…,zN(t)]T，

(19)

H(t)=STS+μLT(diag(‖LiG‖))-1L，

(20)

J′(t)=ST(SG-C)+μLT(diag(‖LiG‖))-1L。

(21)

2.3改进图像重建算法的实现步骤

基于多准则Hopfield网络的ECT图像重建算法的具体实现步骤如下：

1)初始化：对神经网络、算法参数初始化，通过实验本文设置C0=1，τ=1，w1=0.013，w2=0.83，w3=0.13和w4=0.39，γ1=γ2=γ3=γ4=1；以LBP线性反投影算法解U=G0=STC作为初始状态；初始迭代次数t=1，总迭代次数为500次。

4)利用公式(14)计算出Hopfield网络的能量函数。

5)根据更新后的神经元输出Gj(t+Δt)与更新前的神经数值Gj(t)之间的差值进行判断，如果其差值远远小于1(本文选取其差值小于0.001)，则迭代停止，若不满足要求，则继续迭代。

3　仿真实验

为了验证此算法对于解决ECT图像重建问题的有效性，选取8极板方形管道的ECT系统的8种典型流型进行实验，成像时剖分像素为20*20的管道截面，并在matlab平台上做了相关的仿真实验。最后将基于多准则优化的Hopfield图像重建结果与LBP算法和Landweber迭代算法等两种传统图像重建算法进行了比较。

表1　各种算法的图像重建结果

为了便于评价和对比这3种ECT图像重建算法的性能，引入了如下两个指标[19]：图像误差和相关系数。图像误差是指重建图像与原始图像之间的相对误差，利用式(22)进行计算；相关系数是指重建图像与原始图像之间的线性相关程度，通过式(23)进行计算。

(22)

(23)

表2和表3分别为利用LBP线性反投影算法、Landweber迭代算法以及基于多准则的Hopfield网络算法的重建图像与原始图像间的图像误差和相关系数。

表2　各算法重建图像的误差

表3　各算法重建图像的相关系数

从表1、表2和表3可以看出，基于多准则的Hopfied的图像重建算法与线性反投影法、Landweber迭代方法相比，多准则Hopfield网络算法在图像重建质量上要优于其它两种算法，其图像误差更小。同时也可以看出，此算法获得的图像与原始图像间的相关系数更高，即线性相关程度更高。由于多准则Hopfield网络算法在迭代过程中采用了多种评价准则，所以在一定程度上克服了LBP算法与Landweber算法介质边界比较模糊的缺点。由此也证明了所提出的ECT图像重建算法的有效性。

4　结　论

在分析ECT系统基本原理和Hopfield神经网络模型的基础上，提出一种基于多准则Hopfield网络模型的ECT图像重建算法。首先对ECT重建图像的特点进行了分析，确定了重建图像的图像熵、测得电容值与估计出的电容值之间的方差、局部非均匀性函数和峰值性函数之和、图像的总变差等4个评价函数，然后结合Hopfield神经网络模型，给出了Hopfield神经网络模型的能量函数，最后推导出基于多准则Hopfield网络模型的ECT图像重建迭代公式。由于在图像重建迭代过程中多个评价指标的约束，使重建图像的分辨率得到了提高，更能逼近原始图像。通过各种流型的仿真实验也证明了这种算法的可行性。由此可见，多准则Hopfield网络算法是一种有效的和精度较高的ECT图像重建算法，这也为ECT图像重建算法的研究提供了一种新的途径和方法。

[1]Wang H X, Zhang L F. Identification of two-phase flow regimes based on support-vector machine and electrical capacitance tomography [J]. Measurement Science and Technology，2009，20(11): 114007(8pp).

[2]马平，周晓宁，田沛，等. 过程层析成像技术的发展及应用[J].化工自动化及仪表，2009，36(1)：1-5.

MA Ping， ZHOU Xiaoning, TIAN Pei, et al. Develoment and application of process tomography [J]. Control and Instruments in Chemical Industry，2009，36(1)：1-5.

[3]LEI J, LIU S, LI Z H, et al. A multi-scale image reconstruction algorithm for electrical capacitance tomography [J]. Applied Mathematical Modeling，2011, 35(6)：2585-2606.

[4]张建国，马福昌，窦银科. 层析成像在冰水两相流参数测量中的应用[J].光学精密工程，2013，21(8)：1981-1987.

ZAHNG Janguo, MA Fuchang, DOU Yinke. Application of electrical resistance tomography to ice-water two-phase flow parameter measurement [J]. Optics and Precision Engineering, 2013, 21(8)：1981-1987.

[5]陈宇，高宝庆，张立新，等.基于加权奇异值分解截断共轭梯度的电容层析图像重建[J]. 光学精密工程, 2010, 18(3)：701-707.

CHEN Yu，GAO Baoqing，ZHANG Lixin，et al. Image reconstruction based on weighted SVD truncation conjugate gradient algorithm for electrical capacitance tomography [J]. Optics and Precision Engineering，2010，18(3)：701-707.

[6]LEI J,LIU S,LI Z H, et al. An image reconstruction algorithm based on the extended Tikhonov regularization method for electrical capacitance tomography [J]. Measurement，2009，42(3)：368-376.

[7]YANG W Q, SPINK D M, YORK T A, et al. An image reconstruction algorithm based on Landweber’s iteration method for electrical capacitance tomography[J]. Measurement Science and Technology，1999，10(11)：1065-1069.

[8]陈宇，陈德运.基于改进Runge-Kutta型Landweber的电容层析成像图像重建算法[J].电机与控制学报.2014，18(7) ：107-112.

CHEN Yu, CHEN Deyun. Improved Runge-Kutta type Landweber image reconstruction algorithm for electrical capacitance tomography system [J]. Electric Machines and Control，2014，18(7)：107-112.

[9]YANG W Q, PENG L H. Image reconstruction algorithms for electrical capacitance tomography [J]. Measurement Science and Technology，2003，14(1)：R1-R13.

[10]HAO J N, YIN W L, ZHAO Q, et al. Preconditioning of projected SIRT algorithm for electromagnetic tomograpy [J]. Flow Measurement and Instrumentation, 2013, 29:39-44.

[11]阎春生，廖延彪，田芊. 层析成像图像重建算法综述[J].中国光学，2013，6(5): 617-631.

YAN Chunsheng, LIAO Yanbiao, TIAN Qian. Image reconstruction algorithms of computed tomography [J]. Chinese Optics, 2013，6(5)：617-631.

[12]陈德运，郑贵滨，于晓洋,等. 基于遗传算法电容层析成像图像重建算法的研究[J].电机与控制学报,2003,7(3): 207-211.

CHEN Deyun, ZHENG Guibin, YU Xiaoyang, et al. Image reconstruction algorithm based on genetic algorithms for two-phase flow electrical capacitance tomography system [J].Electric Machines and Control, 2003，7 (3)：207-211.

[13]MARASHDEH Q, WARSITO W, FAN L S, et al. A nonlinear image reconstruction technique for ECT using a combined neural network approach [J]. Measurement Science and Technology，2006，17(8)：2097-2103.

[14]吴新杰，黄国兴,王静文.粒子滤波算法在ECT图像重建中的应用[J].光学精密工程，2012，20(8)：1824-1830.

WU Xinjie, HUANG Guoxing, WANG Jingwen. Application of particle filtering algorithm to image reconstruction of ECT [J]. Optics and Precision Engineering,2012,20(8)：1824-1830.

[15]陈德运，高明，李伟等.新型ECT数据采集系统设计与实现[J].电机与控制学报，2013，17(5)：87-92.

CHEN Deyun, GAO Ming, LI Wei, et al. Design and implementation of date acquisition system for the clectrical capacitance tomography[J]. Electric Machines and Control，2013，17 (5)：87-92.

[16]WANG Y, WAHL F M. Multiobjective neural network for image reconstruction [J]. IEE Proceedings-Vision, Image and Signal Processing, 1997, 144(4): 233-236.

[17]WARSITO W, FAN L S. Neural network based multi-criterion optimization image reconstruction technique for imaging two- and three-phase flow systems using electrical capacitance tomography [J]. Measurement Science and Technology,2001，12(12): 2198-2210.

[18]王化祥，唐磊，闫勇. 电容层析成像图像重建的总变差正则化算法[J].仪器仪表学报，2007，28(11)： 2014-2018.

WANG Huaxiang,TANG Lei, YAN Yong. Total variation regularization algorithm for electrical capacitance tomography [J]. Chinese Journal of Scientific Instrument，2007，28(11)：2014-2018.

[19]彭黎辉，陆耿，杨五强. 电容成像图像重建算法原理及评价[J].清华大学学报，2004，44(4): 478-483.

PENG Lihui, LU Geng, YANG Wuqiang. Image reconstruction algorithms for electrical capacitance tomography [J]. Journal of Tsinghua University，2004，44(4)：478-483.

(编辑：贾志超)

Image Reconstruction by using Multi-criteria of Hopfield Network for ECT

WU Xin-jie1,HE Zai-gang1,LI Hui-qiang1,ZHENG Jing-na1,CHEN Ling1,XU Chao1,CHEN Yue-ning1,YAN Hua2

(1. College of Physics, Liaoning University, Shenyang 110036, China；2. School of Information Science and Engineering，Shenyang University of Technology，Shenyang 110870，China)

In view of low image reconstruction quality of electrical capacitance tomography (ECT), an image reconstruction algorithm of ECT based on multi-criteria of Hopfield network is put forward. Firstly, the basic principle of ECT image reconstruction and Hopfield network was analyzed. Secondly, according to the characteristics of the ECT image reconstruction, four criterion functions were determined,including image entropy, the error sum of squares between measuring capacitances and estimating capacitances, local heterogeneity function of reconstruction image, and total variation of reconstruction image. These four criteria functions were introduced to the energy function of Hopfield network,and thus the dynamic equations of Hopfield networks were deduced. On this basis, the iterative algorithm for ECT image reconstruction was gained. Finally, the proposed method was verified through simulation experiment. Simulation results show that the error of image reconstruction and correlation coefficient are better than corresponding indicators obtained by LBP and Landweber iterative algorithm.This ECT image reconstruction method is proven to be highly effective and accurate.It also provides an effective method and means for ECT image reconstruction algorithm.

electrical capacitance tomography; image reconstruction; hopfield network; multi-criteria; image error

2015-01-15

辽宁省教育厅科研项目(L2014003)；国家自然科学基金(61071141)

吴新杰(1964—)，男，博士，教授，研究方向为层析成像技术、智能优化算法、信号处理方法及其应用；

何在刚(1989—)，男，硕士，研究方向为神经网络、电容层析成像技术；

吴新杰

10.15938/j.emc.2016.08.013

TP 319.4

A

1007-449X(2016)08-0098-07

李惠强(1990—)，男，硕士研究生，研究方向为检测技术、层析成像技术的应用；

郑静娜(1990—)，女，硕士研究生，研究方向为电磁层析成像技术和智能优化算法及其应用；

陈玲(1989—)，女，硕士研究生，研究方向为电容层析成像技术的应用；

许超(1981—)，男，硕士，实验师，研究方向为信号处理和单片机技术；

陈跃宁(1960—)，男，博士，副教授，研究方向为光电子器件；

颜华(1964—)，女，教授，博士生导师，研究方向为层析成像检测技术、信号处理、虚拟仪器。