广义Maxwell阻尼器高层结构随机风振响应解析法

李创第,王磊石,邹万杰,葛新广,李　暾

(1.广西大学土木建筑工程学院， 广西南宁530004；2.广西科技大学土木建筑工程学院， 广西柳州545006)



广义Maxwell阻尼器高层结构随机风振响应解析法

李创第1,2,王磊石1,邹万杰2,葛新广2,李暾2

(1.广西大学土木建筑工程学院， 广西南宁530004；2.广西科技大学土木建筑工程学院， 广西柳州545006)

为解决设置广义Maxwell阻尼器的非定常耗能结构在随机风荷载作用下的随机响应采用传统方法比较繁琐及精度不高的问题，针对此类结构提出基于传递函数法的精确分析方法。首先，用微分积分混合方程组建立了结构的动力运动方程；其次用传递函数法及巴斯金相关函数的随机风振激励模型，获得了结构用第一振型表达的时域瞬态位移响应非扩阶解析解；然后，根据获得的解析解，运用随机振动方法获得了该类型耗能结构第一振型下的随机风振响应及楼层处等效静态风荷载设计取值的解析解，最后通过算例计算显示：设置阻尼器后结构的位移减少约36.7%，同时与数值方法计算结果完全吻合，证明了本文方法的优越性。由于采用巴斯金相关函数的随机风振激励模型，本文方法可以应用其他诸如地震、路面不平等激励下的振动响应。

广义Maxwell阻尼器；高层建筑结构；随机风振；风载取值；解析解

0　引　言

目前广泛应于建筑结构的抗风耗能结构众多，但其中粘滞阻尼器及粘弹性阻尼器由于其优良的减振效果及简便的工程应用[1-2]，日益受到研究人员的重视。由于实际风荷载具有随机性的特性，故对粘弹性阻尼器耗能高层结构随机风振响应的分析具有理论和实际工程意义。Maxwell模型阻尼器本构方程简单，易于扩阶，模型计算参数便于从试验数据拟合[3-4]，且一般流体阻尼器和粘弹性阻尼器均可用Maxwell模型近似表示或用广义Maxwell模型表示[1-4]，故基于Maxwell模型阻尼器的耗能结构动力响应特性分析日益受到重视[5-8]。Maxwell阻尼耗能结构的现有解析分析方法分为扩阶复模态法和非扩阶近似法两类。扩阶复模态法主要是引入状态变量对运动方程进行扩阶，将Maxwell阻尼耗能结构的动力运动方程化为一阶状态方程组求解，目前非扩阶近似法已用于耗能结构平稳随机地震响应的数值分析[6-8]，但因扩阶方程组物理意义不明确，变量个数剧增，计算效率低，使该法的实际应用受到限制；非扩阶近似法有模态应变能法[1-2,9]和强行解耦法[10]。当前非扩阶近似法得到广泛应用，但该法采用频域建模方式会导致耗能结构方程不能严格适用于强风和地震等非简谐激励的时域分析，且近似假设过多，精度较低和适用范围有限[8]。

针对上述方法的不足，本文提出一种兼顾精确和效率的优效方法。由于传递函数法不用扩阶，可直接获得一般粘滞阻尼对称线性定常结构的脉冲响应函数的精确解[11]。设置粘弹性阻尼器的建筑耗能结构，其具有频率依赖的特性，目前对于该类型的结构传递函数法研究较少。当前随机脉动风速(或风压)有两种表达方式，一种是应用功率谱表达式[12]，另一种是应用相关函数表达式[13-15]，由于功率谱和相关函数存在一一对应的傅氏变换关系，因此这两种表达式在本质上是完全一样的。因巴斯金提出的相关函数表达式包含有4个可调参数，可以统一表示工程上相当广泛的一类随机激励，适用范围更广。为使分析方法更具一般性，本文采用巴斯金相关函数表征脉动风速或风压随机特性，应用传递函数方法获得设置广义Maxwell耗能结构受随机风振作用的结构响应的分析法。

1　运动方程

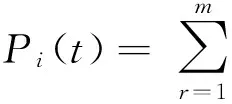
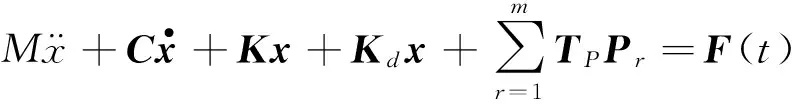
(1)

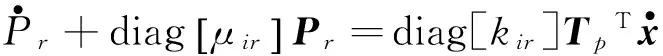
(2)

式中：Kd为ki0组成的三对角平衡刚度(或模量)矩阵，i=1～n，r=1～m，且：

其中：i=1～n，r=1～m，x0= 0。

由式(1)、式(2)，可得结构的微分积分混合方程为：

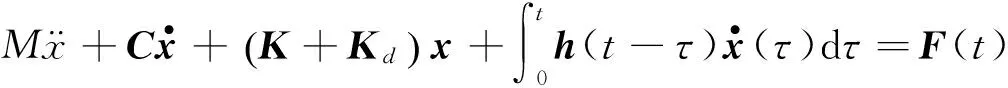
(3)

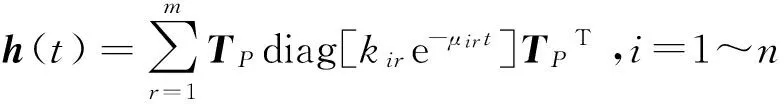
由于在风荷载作用下，高层建筑结构振动响应主要受第一振型控制[16]，故高层结构的楼层处位移x按结构第一振型φ1展开：

x=φ1y1,

(4)

式中：y1为结构第一振型广义坐标变量。

则结构方程(3)化为

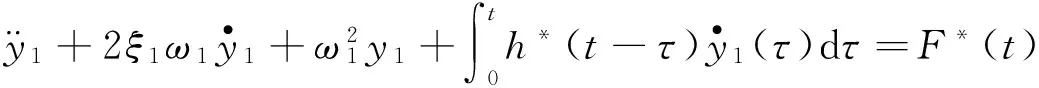
(5)

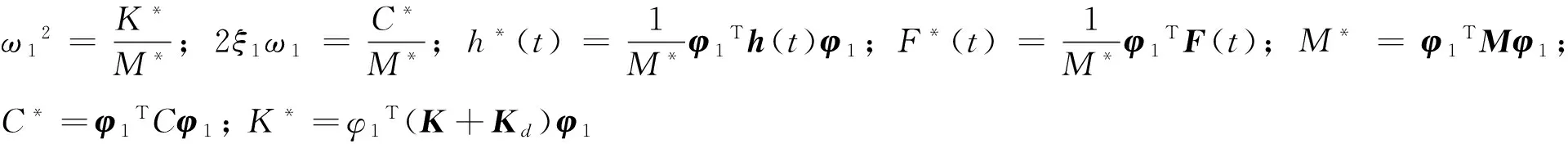
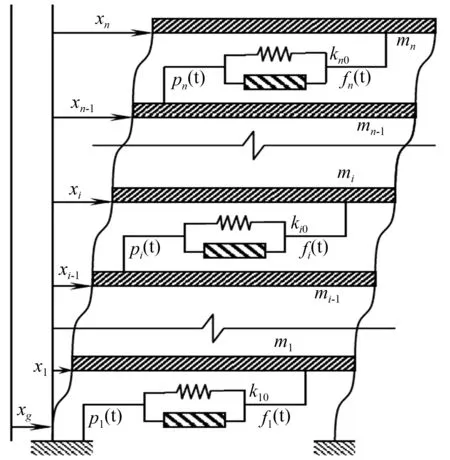
图1广义Maxwel阻尼耗能结构计算简图

Fig.1Calculation diagram of energy dissipation structure with generalized Maxwell damper

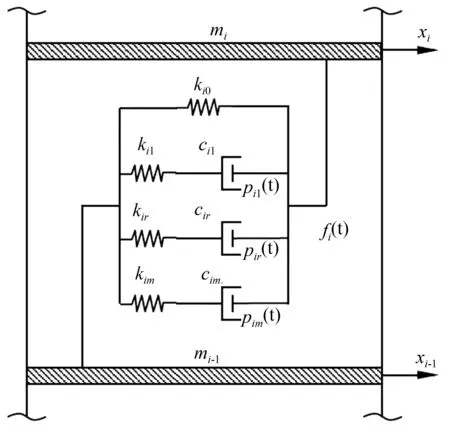
图2第i层广义Maxwel阻尼器fi(t)计算简图

Fig.2Calculation diagram of generalized Maxwell damper of theilayer

2　基于传递函数法的瞬态响应分析

2.1结构特征值分析

设广义位移初始条件为：

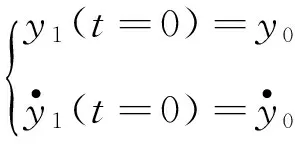
(6)

用拉氏公式对式(5)进行变换：

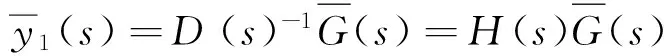
(7)

其中：

(8)

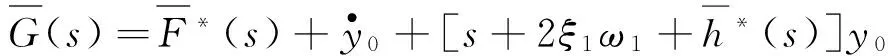
(9)

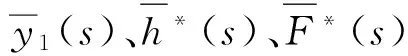
结构特征值方程为：

D(s)=0。

(10)

由式(10)可求出N个特征值sj，显然，N=mn+2，说明耗能结构的振动方程特征值由mn个负实数及一对共轭复数组成。

2.2传递函数解析式

根据耗能结构振动方程的特征值sj是传递函数H(s)极点的原理，传递函数可用下列多项式表示[16]：

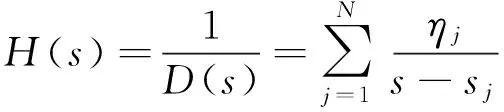
(11)

式中：ηj为待定常数。

根据洛必达法则可求出待定常系数ηj为：

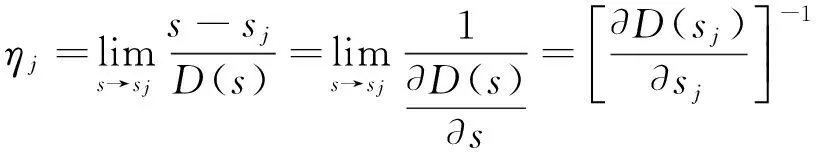
(12)

2.3广义位移时域响应解析解

由式(8)、(9)、(11)、(12)可得：

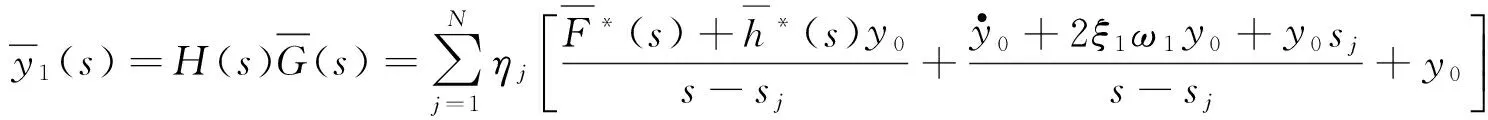
(13)

对式(13)作拉氏逆变换，由此可以获得广义位移(或坐标)的时域响应解析解为：

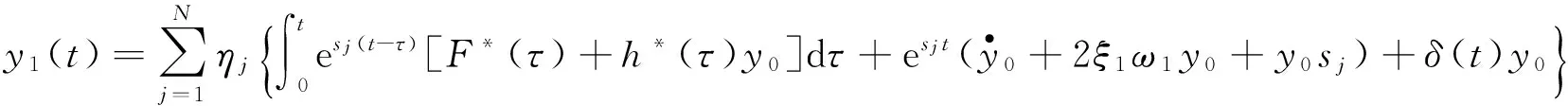
(14)

式中：δ(·)为Dirac delta 函数。

t>0时，广义位移(或坐标)的响应可进一步表示为：

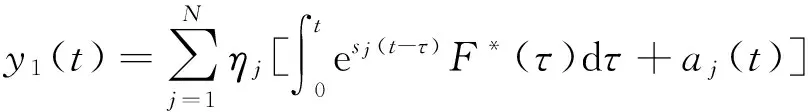
(15)

式中：aj(t)表示由初始条件对结构产生的响应影响，且：

(16)

对于零初始条件，aj(t)=0,j=1～N。

3　基于巴斯金相关函数的脉动风荷载模型

3.1基于巴斯金相关函数的平稳激励模型

基于巴斯金相关函数，对均值为零的平稳随机过程激励f(t)，可知其相关函数Rf(τ)与谱密度函数Sf(ω)存在以下关系[15]：

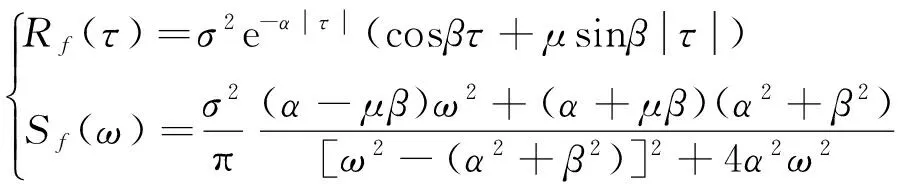
(17)

式中：τ和ω分别为f(t)的时差和频率变量；σ2、α、β、μ分别为f(t)的方差、相关因子、卓越频率因子和正弦函数参与因子。

式(17)中，σ2、α、β、μ为可调参数，当这些参数取不同组合时，可表示工程上广泛应用的平稳随机过程模型，具体如下：

①当σ2=1时，有：

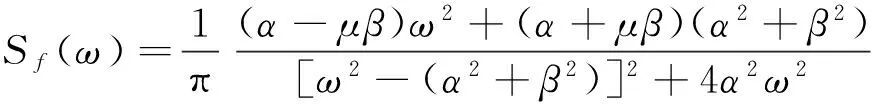
(18)

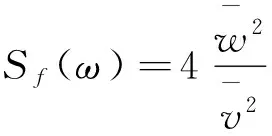
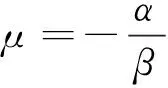
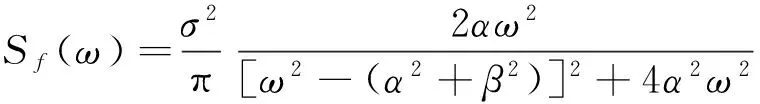
(19)

式(19)常用来表达脉动风的随机风速谱[14-15,18]。

③当μ=0时，有：

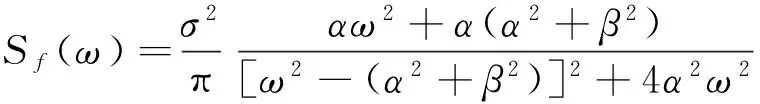
(20)

式(20)作为有界噪声模型[19-21]，不仅可以模拟宽带和白噪声模型激励，也可模拟窄带过程激励。式(20)也常作为脉动风速谱[22-23]、随机地震谱[14]和轨道及路面谱[24]。

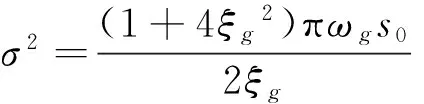
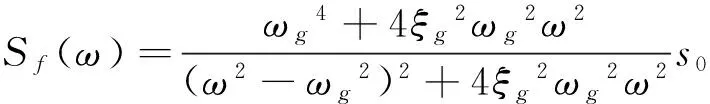
(21)

式(21)为结构地震工程分析中使用较多的Kanai-Tajimi地震谱[14]，其中：ωg为结构所在地的地面特征频率；ξg是结构所在地的地面特征阻尼比；s0是激励谱常数，其数值可反映地震动的强弱程度。

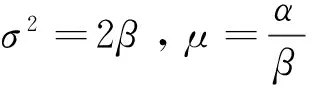
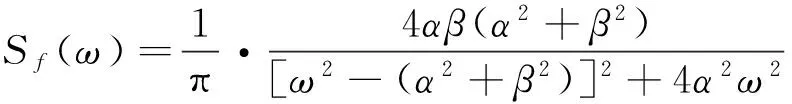
(22)

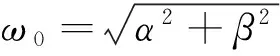
⑥当σ2=1，β=0，μ=0时，有：

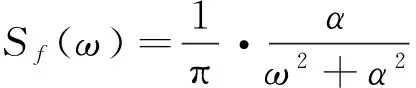
(23)

式(23)用来表示基于白噪声输入的一阶线性滤波器的平稳输出，常作轻轨路面谱激励模型[27]。

⑦当σ2=α，β=0，μ=0，且α→∞时，有：

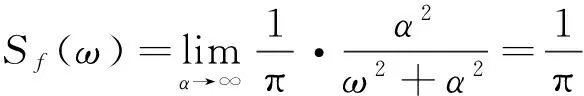
(24)

此时，巴斯金谱即退化为理想白噪声模型激励谱。

⑧当σ2=1，α=0，μ=0时，有：

Rf(τ)=cosbπ，

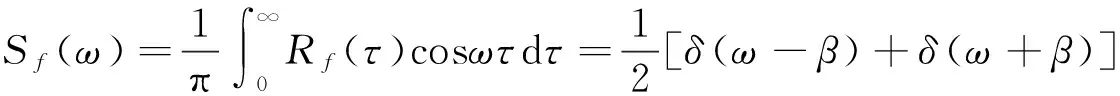
(25)

式中：δ(·)为dirac delta函数。

式(25)为随机正弦波f(t)=sin(βt+φ)模型的激励谱密度函数表达式，其中，相位φ在(0,2π)上满足均匀随机分布特点。

综上所述，巴斯金相关函数统一描述工程上相当广泛的平稳随机激励，从无限小带宽的随机正弦波到无限大带宽的白噪声。采用这一激励模型的好处是易于获得响应相关特性的解析表达式，如响应的功率谱与各阶谱矩的解析公式等，这在结构的动力可靠性分析方面是重要的[14]。

3.2基于巴斯金函数的脉动风载模型

在高度为Hi的楼层处，建筑结构所受的脉动风荷载Fi(Hi,t)为[18]：

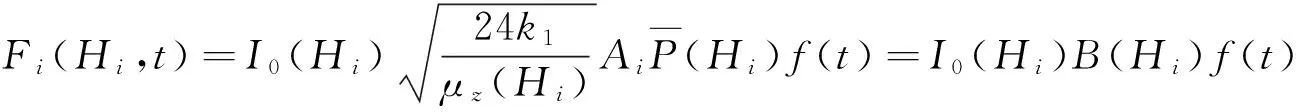
(26)

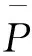
当规格化脉动风速平稳随机过程f(t)用巴斯金相关函数及其谱密度表示时，表达式为[18]：

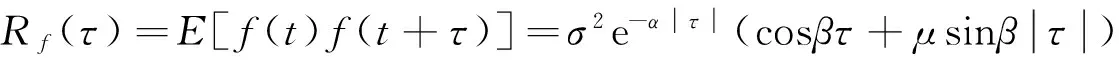
(27)

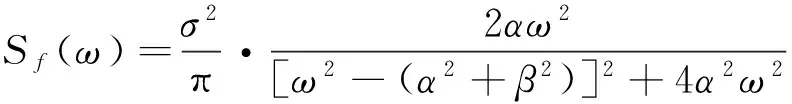
(28)

其中：E[·]表示取函数期望值；

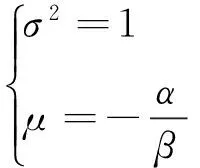
(29)

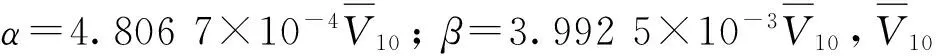
由于脉动风荷载具有竖向高度的相关性，为此，脉动风荷载Fi(Hi,t)与Fj(Hj,t)的存在关系[11]：

E[Fi(Hi,t)Fj(Hj,t)]=ρijB(Hi)B(Hj)Rf(τ),

(30)

式中：Rf(τ)用式(27)表示，其参数σ2、μ、α、β按式(29)计算。

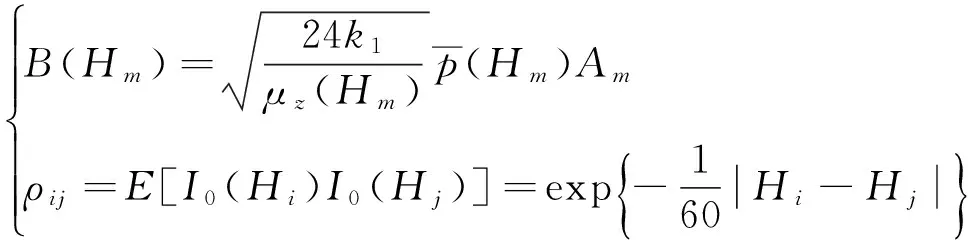
(31)

4　耗能结构平稳随机风荷载作用下的位移响应分析

由式(15)和式(26)，可得广义位移(或坐标)响应y1(t)的平稳解为：

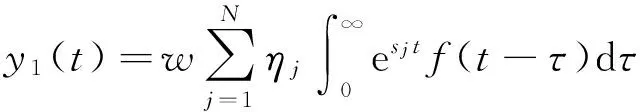
(32)

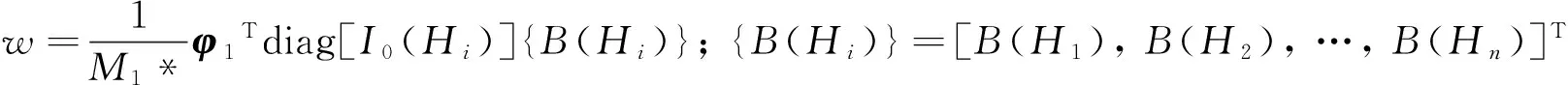
故平稳响应y1(t)的相关函数为：

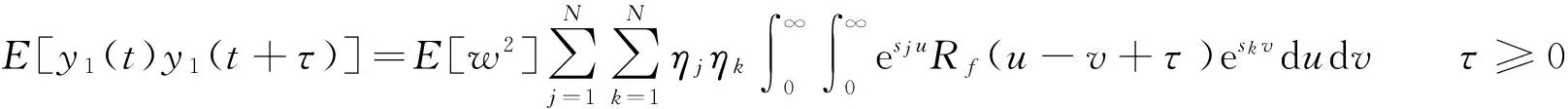
(33)

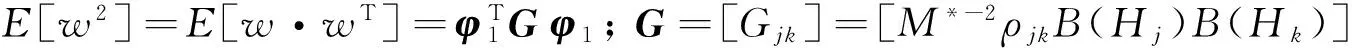
令：

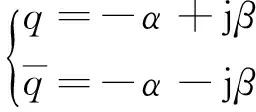
(34)

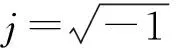
利用欧拉公式：

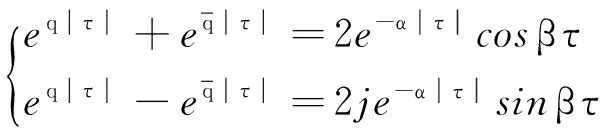
(35)

将Rf(τ)的表达式(27)改写为：

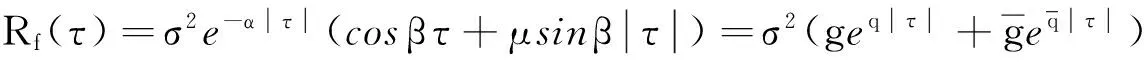
(36)

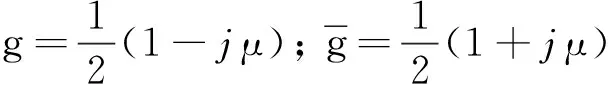
则y1(t)的相关函数表达式(33)可化为：

(37)

式中：

(38)

将式(38)代入式(37)，y1(t)的相关函数表达式简化为：

(39)

式中：

(40)

特别的，令τ=0，得广义位移(或坐标)y1的平稳方差解析解为：

(41)

5　结构设计响应分析

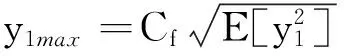
(42)

对于结构所受风载的计算，我国《荷载规范》(GB50009-2012)规定峰值因子Cf=2.5，故由式(42)可求得广义位移y1的设计响应值y1max。

由于式(4)推导时，是对结构位移按第一振型展开的：

x(t)=φ1y1(t)。

(43)

因此，耗能结构各楼层处的风振动位移响应设计值：

Xmax=φ1y1max。

(44)

6　耗能结构楼层处等效静态风荷载取值计算

由于耗能结构总刚度矩阵K+Kd、质量矩阵M与其第1振型φ1及频率ω1存在恒等关系：

(K+Kd)φ1=ω12Mφ1，

(45)

故：

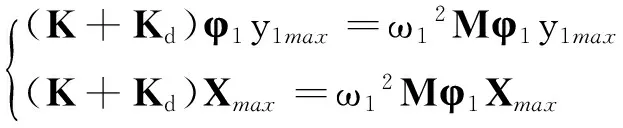
(46)

故要使结构产生的设计位移向量为Xmax，需施加的等效风振力向量为ω12MXmax，所以原主体结构第i楼层的等效风振力分量Pdi为：

Pdi=ω12miXimax=ω12miφi1y1max,

(47)

式中：mi为结构第i层的楼层质量；φi1为耗能结构第一振型φ1在第i层处的振型分量。

耗能结构顺风向风压作用效应可等效为平均风压与风振动压力共同作用的总效应。因此，耗能结构在第i层楼层处的顺风向等效静态风荷载设计取值可用下式表示：

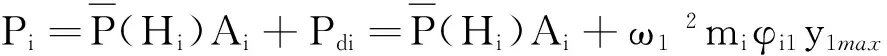
(48)

7　算　例

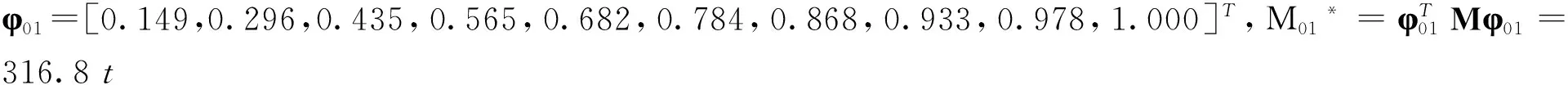
用本文方法获得的结构风振位移设计响应解析解和用数值积分获得的风振位移设计响应数值解完全相同，如图3所示(图形已重合),从而验证了方法的正确性。图3给出了有无阻尼器控制的结构风振位移响应设计值的对比曲线，表1和表2分别列出了结构在是否设置阻尼器的情况下，各楼层的位移、等效静态设计风荷载取值。计算结果表明，与无阻尼器控制相比，结构的位移设计响应减小了约36.7%。由此可见，阻尼器对于风振的减振效果是较为明显的。

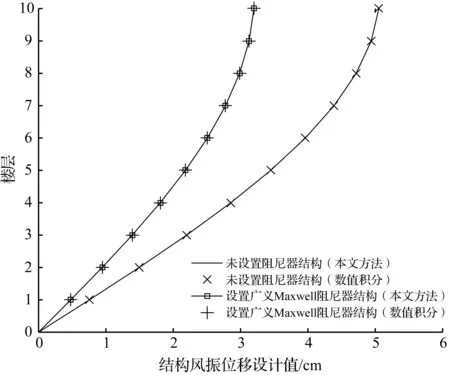
图3　结构风振位移设计值

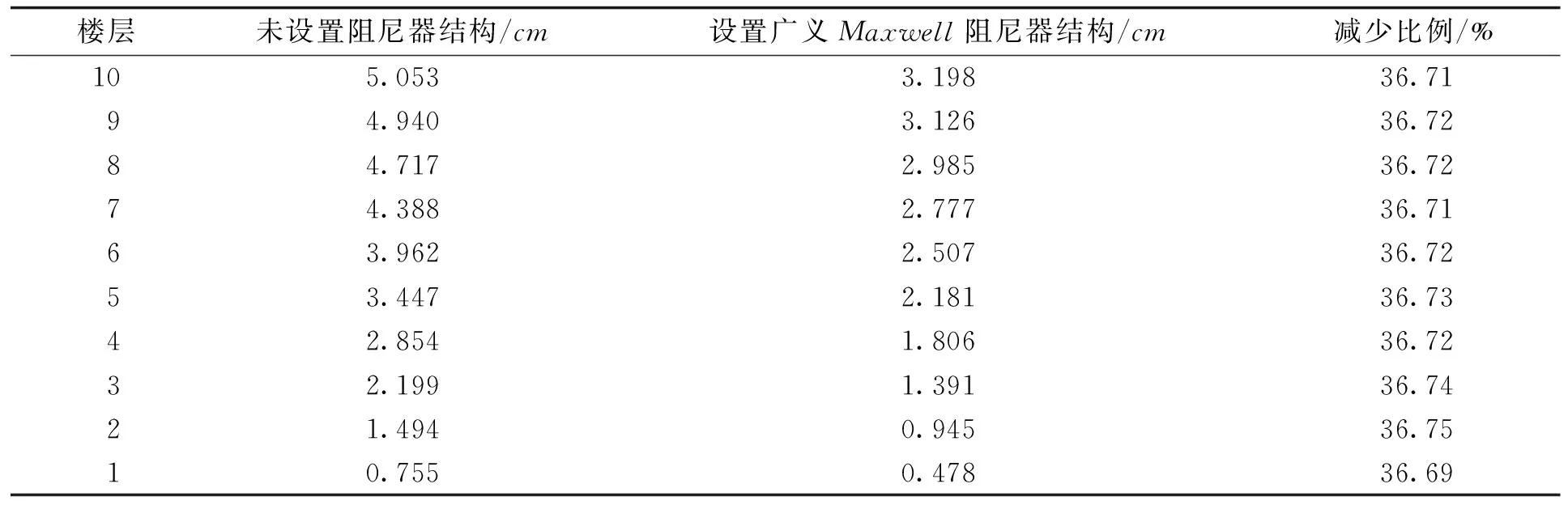
楼层未设置阻尼器结构/cm设置广义Maxwell阻尼器结构/cm减少比例/%105.0533.19836.7194.9403.12636.7284.7172.98536.7274.3882.77736.7163.9622.50736.7253.4472.18136.7342.8541.80636.7232.1991.39136.7421.4940.94536.7510.7550.47836.69

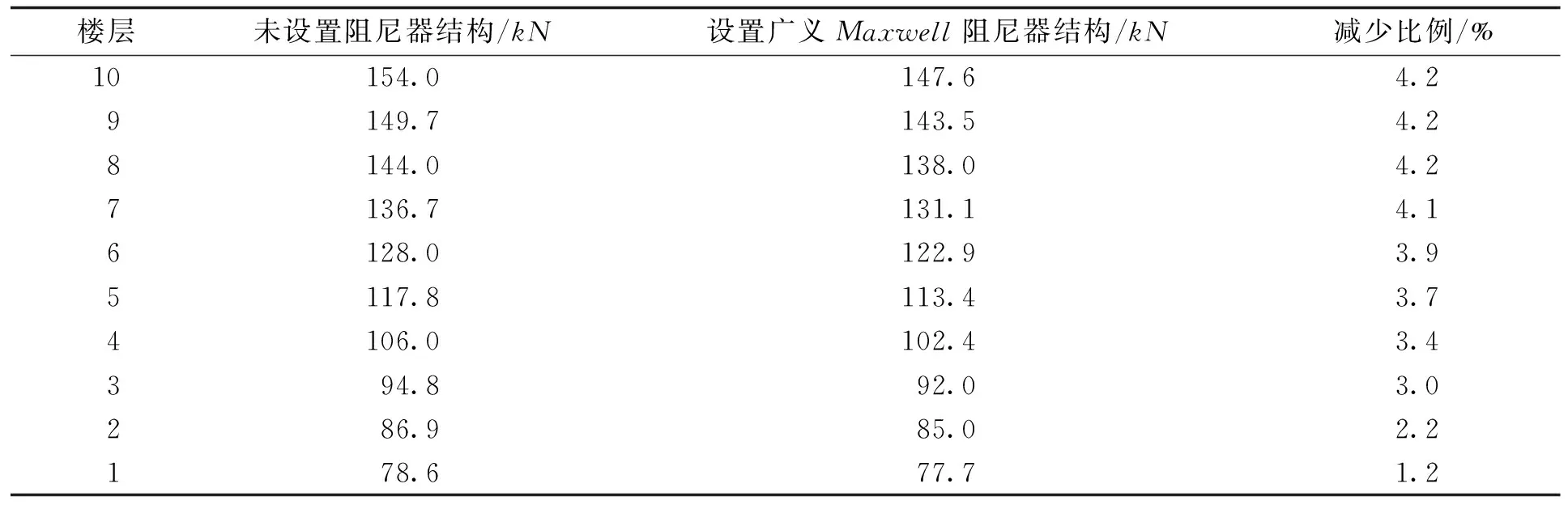
表2　结构等效静态设计风荷载取值Tab.2　The design value of structural equivalent static wind load

8　结　语

本文通过对设置广义Maxwell阻尼器的高层建筑耗能结构在随机风荷载激励下振动响应和等效静态风荷载设计取值进行了探究。首先，利用传递函数法对此类结构在随机风振下的响应进行精确分析，并通过算例验证了该方法相对与传统方法具有精度高、计算量少的优点。其次，将复杂的随机振动设计方法简化为静态等效设计方法，有助于此类被动控制结构在具体工程中推广应用。此外，由于文中采用巴斯金相关函数及其谱密度函数作为一类典型的平稳随机激励，在工程分析中具有广泛的代表性，可以用来描述诸如随机风载、地震激励、路面或轨道的随机起伏以及有界噪声激励等激励模型，故本文基于巴斯金模型随机激励所获得的结构响应相关特性的解析解具有较好的工程应用意义。

[1]CHRISTOPOULOSC,FILLIATRULTA.Principleofpassivesupplementaldampingandseismicisolation[M].Pavia,Italy:IVSSPress, 2006.

[2]李创第，邹万杰，葛新广，等.多自由度一般积分型粘弹性阻尼器减震结构的随机响应与等效阻尼[J]. 工程力学，2013，30(4)：136-145.

[3]PASKSW.Analyticalmodelingofviscoelasticdampersforstructuralandvibrationcontrol[J].InternationalJournalofSolidsandStructures, 2001,38:8065-8092.

[4]CHANGTS,SINGHMP.Mechanicalmodelparameterforviscoelasticdampers[J].JournalofEngineeringMechanics, 2009, 135(6):581-584.

[5]YAMADAK.DynamiccharacteristicsofSDOFstructurewithMaxwellelement[J].JournalofEngineeringMechanics, 2008, 134(5):396-404.

[6]PALMERIA,RICCIARDELLIF.Statespaceformulationforlinearviscoelasticsystemwithmemory[J].JournalofEngineeringMechanics, 2003, 129(7):715-724.

[7]SINGHMP,VERMANP.SeismicanalysisanddesignwithMaxwelldampers[J].JournalofEngineeringMechanics, 2003，129(3):273-282.

[8]PALMERIA.Correlationcoefficientsforstructureswithviscoelasticdampers[J].EngineeringStructures, 2006, 28:1197-1208.

[9]瞿伟廉，程懋堃，毛增达,等.设置粘弹性阻尼器钢结构高层建筑抗震抗风设计的实用方法[J]. 建筑结构学报，1998,19(2)：42-49.

[10]OUJP,LONGX,LIQS.Seismicresponseanalysisofstructureswithvelocity-dependentdampers[J].JournalofConstructionalSteelResearch, 2007, 63:628-638.

[11]廖伯瑜，周新民，君志宏.现代机械动力学及其工程应用：建模、分析、仿真、修改、控制、优化[M]. 北京：机械工业出版社，2003:175-179.

[12]张相庭.结构风压和风振计算[M]. 上海：同济大学出版社，1985:60-70.

[13]陈英俊，于希哲.风荷载计算[M]. 北京：中国铁道出版社，1998:80-100.

[14]李桂青，李秋胜.工程结构时变可靠度理论及其应用[M]. 北京：科学出版社，2001:195-205.

[15]李桂青.抗震结构计算理论和方法[M]. 北京：地震出版社，1985:232-259.

[16]李创第,尉霄腾,王磊石,等.积分型粘弹性阻尼器耗能结构瞬态响应的精确解[J]. 广西大学学报(自然科学版),2016,41(1):83-90.

[17]吴瑾，夏逸鸣，张丽芳.土木工程结构抗风设计[M]. 北京：科学出版社，2007:47-48.

[18]杨庆山，沈世钊.悬索结构随机风振反应分析[J]. 建筑结构学报，1998,19(4)：29-39.

[19]XIEWC.Momentlyapunovexponentsofatwo-dimensionalsystemunderboundednoiseparametricexcitation[J].JournalofSoundandVibration, 2003, 263(3): 593-616.

[20]ZHUJ,XIEWC,SORM,etal.Parametricresonanceoftwodegreesoffreedomsysteminducedbyboundednoise[J].JournalofAppliedMechanics, 2009, 76(4):1-13.

[21]刘雯彦，陈忠汉，朱位秋.有界噪声激励下单摆—谐振子系统的混沌运动[J]. 力学学报,2003,35(5):634-639.

[22]LINYK，LIQC.NewstochastictheoryforbridgesstabilityinturbulentflowⅡ[J].JournalofEngineeringMechanics, 1995, 121(1): 102-116.

[23]ZHUJ,WANGQC,XIEWC.Flow-inducedinstabilityunderboundednoiseexcitationincross-flow[J].JournalofSoundandVibration,2008,312: 476-495.

[24]DIMENTBERGM.Stabilityandsubcriticaldynamicsofstructureswithspatiallydisorderedtravellingparametricexcitation[J].ProbabilisticEngineeringMechanics, 1991,7: 131-134.

[25]DAVISBR,THOMPSONAG.Powerspectraldensityofroadprofiles[J].VehicleSystemDynamics, 2001,35: 409-415.

[26]BOLOTINVV.Randomvibrationofelasticsystems[M].TheHague,Holland:MartinusNijhoff,1984.

[27]胡津亚，曾三元.现代随机振动[M]. 北京：铁道出版社,1989.

(责任编辑唐汉民梁健)

Analytic method for random wind-induced response of high-rise structure with general Maxwell dampers

LI Chuang-di1,2, WANG Lei-shi1, ZOU Wan-jie2，GE Xin-guang2, LI Tun2

(1.Institude of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China;2.Institude of Civil Engineering and Architecture, University of Science and technology of Guangxi, Liuzhou 545006, China)

An accurate analytic method based on transfer function is applied to solve the response of high-rise structures equipped with General Maxwell dampers under random wind load, while traditional methods are relatively complicated and low precision. Firstly, structural dynamic integral-differential response equations are established. Secondly, by using transfer function method, the exact solutions of structural transient response in time-domain are obtained by expanding the structural response with respect to the first mode. Thirdly, analytical solution of wind-induced structural random response and equivalent static design wind load of high-rise structure with general Maxwell dampers are obtained by using random vibration method. Finally, a numerical example is provided to show that the displacement of the structure with dampers is reduced by about 36.7% against that without dampers, and the results given by the proposed method are in good agreement with the numerical method, so the advantages of the method are proved. In addition, due to the adoption of Baskin correlation function of random wind vibration excitation model, the proposed method can be applied to excitation response induced by earthquake, random fluctuation of pavement or track, and so on.

General Maxwell damper; high-rise structure; wind-induced random response; wind load; analytic solution

2016-03-15；

2016-06-17

国家自然科学基金资助项目(51468005, 51368008)；广西自然科学基金项目(2014GXNSFAA118315)；广西科技大学创新团队支持计划项目(2015)

李创第(1964—)，男，广西柳州人，广西科技大学教授，博士； E-mail：lichuangdi1964@163.com。

10.13624/j.cnki.issn.1001-7445.2016.0953

TU311.3

A

1001-7445(2016)04-0953-11

引文格式：李创第,王磊石,邹万杰,等.广义Maxwell阻尼器高层结构随机风振响应解析法[J].广西大学学报(自然科学版)，2016，41(4)：953-963.