非矩形相控阵的抗主瓣干扰与单脉冲测角技术
陈新竹,姜媛媛,舒 汀,郁文贤
(1. 上海交通大学 上海市智能探测与识别重点实验室, 上海 200240)(2. 上海航天电子技术研究所, 上海 201109)
非矩形相控阵的抗主瓣干扰与单脉冲测角技术
陈新竹1,姜媛媛2,舒汀1,郁文贤1
(1. 上海交通大学 上海市智能探测与识别重点实验室,上海 200240)(2. 上海航天电子技术研究所,上海 201109)
在传统的数字波束形成雷达系统中,为了抑制主瓣干扰,并保持对目标单脉冲角度估计的精度,需要同时形成四个波束。对于大型的雷达天线阵列,数字波束形成通常在子阵上完成。但是对于非矩形天线阵结构,传统的自适应波束形成架构不再适用,单脉冲角度估计的精度会大幅降低。文中针对非矩形平面阵列,提出一种新的自适应波束形成方法。首先,需要对四个接收波束的输出做线性补偿,该补偿因子可通过阵列流形精确计算获得;其次,进行自适应主瓣干扰对消处理;再进行二维数字单脉冲测角。文中在理论推导的基础上,结合相控阵雷达阵列实例给出仿真结果,验证了该方法的有效性。
自适应数字波束形成;抗主瓣干扰;单脉冲测角;非矩形平面阵;线性补偿
0 引 言
随着电子技术的飞速发展,现代雷达系统面临的电磁环境日益复杂,各种形式的有源和无源干扰,以及地(海)杂波等给雷达的目标检测、定位和跟踪等带来极大的困难。其中,有源干扰通过接收天线的主瓣或副瓣进入雷达接收机和信号处理系统,严重影响雷达系统的探测性能。因此,雷达抗干扰已发展成当前雷达工程和学术领域非常热门和重要的技术。
当有源干扰来自天线副瓣区域时,相控阵雷达可采用副瓣隐匿、超低副瓣天线或自适应副瓣置零等技
术抑制副瓣干扰。这些技术目前已在实际工程中广泛应用,并取得良好的效果[1-2]。若干扰来自天线主瓣区域,由于主瓣宽度窄,增益高,此时抑制副瓣干扰的方法已对主瓣干扰完全失效。因此,如何有效地抑制主瓣干扰,已经成为现代雷达对目标进行精确定位的关键问题,也是雷达电子反对抗中亟待解决的难题。
存在抗主瓣干扰时,相控阵雷达可采用四个高增益波束通过最大似然估计法确定目标角度[3],但主要缺陷在于完成搜索所需的巨大计算量,使得该技术很难在实际应用中实现。而基于四波束的传统自适应数字波束形成信号处理架构[4],可以同时抑制主瓣干扰并完成对目标的单脉冲角度估计。在此基础上,文献[5]提出了
两级的信号处理架构,可以同时抑制副瓣和主瓣干扰。随着大型天线阵列的广泛使用,文献[6]基于子阵提出了抗主瓣干扰和目标角度估计的改进方法。但总的来说,以上方法都只适用于矩形天线阵列。而对于非矩形阵列,存在主瓣干扰时,利用上述方法估计目标的角度,测角精度将有所下降。
本文重点研究自适应数字波束合成抗主瓣干扰和单脉冲测角技术在非矩形阵列中的应用问题,并提出了一种有效的解决方法。
1 传统的自适应波束形成结构及原理
传统自适应数字波束形成架构[4]如图1所示,包括三部分:(1)四个非自适应接收波束的形成,(2)自适应主瓣干扰消除,(3)利用已有的查找表作二维(俯仰和方位维)角度估计。在传统的比幅单脉冲测角中,通常并不形成差差(ΔΔ)波束,而在此架构中,正是利用ΔΔ波束自适应消除了主瓣干扰。此外,原有的单脉冲查找表仍可用来估计目标角度,这与没有主瓣干扰情况下的比幅测角流程十分相似。
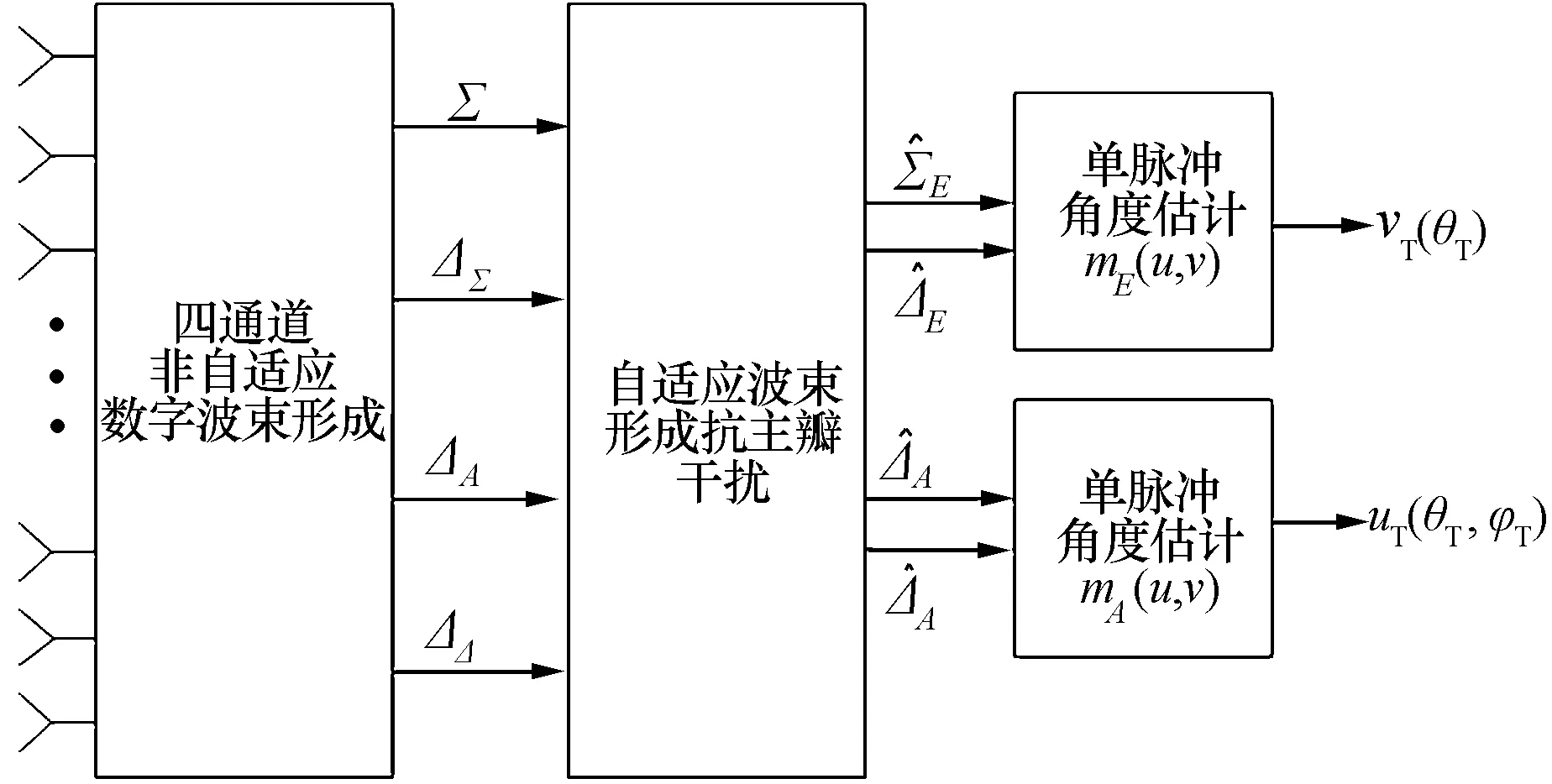
图1 传统的自适应数字波形信号处理结构
对于子阵级的数字波束合成,该结构仍然适用。设平面相控阵由Nx×Ny个全向阵元组成,阵元间距均为半波长,被划分为4个相同的的子阵,如图2a)所示。首先,在每一个子阵内,T/R组件完成模拟的波束形成;然后对子阵的输出做数字加权,分别形成和(Σ),方位差(ΔA),俯仰差(ΔE),差差(ΔΔ)波束。整个平面阵可以被视为一个含有四个超元[7]的阵列,每个超元被放置在对应子阵的相位中心。因此,整个平面阵的和波束方向图可表示为
yi(v-v0))]
(1)
式中:κ为2π/λ;(xi,yi)为第i个子阵相位中心的坐标(以阵列的中心为原点); fsub,i(u,v)为第i个子阵的波束方向图(以该子阵的中心为原点);(u0,v0)是波束指向的方位余弦值,具体表达式为
(2)
式中:φ0和θ0分别是波束指向的方位和俯仰角度。
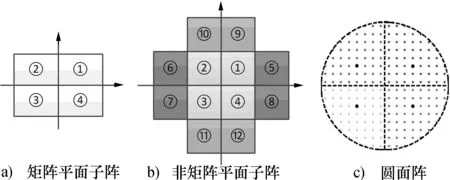
图2 常见的几种平面阵列
由于四个子阵完全相同,所以子阵的波束方向图可以用同一个函数fsub(u,v)表示。此外,注意到子阵关于x,y轴对称,因此该阵列的Σ波束方向图可表示为
fΣ(u,v)=fsub(u,v)*4cos(κ(u-u0)x1)·
cos(κ(v-v0)y1)=
fsub(u,v)*fsup-Σ(u,v)
(3)
同理,ΔA, ΔE, ΔΔ波束方向图表示为
(4)
为了简化推导,在此没有在子阵级作幅度加权。易得,该阵列的Σ波束方向图在阵列指向(u0,v0)处取得峰值;ΔA波束方向图沿着u0形成零陷;ΔE波束方向图沿着v0形成零陷;ΔΔ波束方向图沿着u0和v0都形成零陷。
因此,传统的单脉冲比定义为
(5)
如图3a),mA(u,v)的实部(或虚部)在主瓣范围内随u单调变化。因此,利用波束输出比rΔA/rΣ和已有的查找表,可以精确给出目标的方向余弦值uT,同理,可得到vT。
理论上,式(5)中的单脉冲比也可以用ΔΔ波束定义
(6)
将式(3)、式(4)代入式(5)、式(6),可以得到
(7)

基于上文中的四通道非自适应波束方向图,下面生成自适应方向图
(8)
其中,自适应权wa和we可以用互相关的方法得到[7],具体如下
(9)
图3 基于图2a)中的矩形子阵,波束指向(0,0)
其中,互相关值RΣΔA为
(10)
其他互相关值和自相关值可类比得到。
利用式(8),进一步给出自适应的单脉冲比
(11)
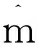
需要注意的是,虽然存在主瓣干扰时,自适应数字波束形成可以应用于子阵级单脉冲角度估计,但是仅仅建立在传统的单脉冲比与自适应的单脉冲比相等的前提下,如式(7)。也就是说,要求该天线阵列的每个子阵流形相同且关于阵列的中心彼此对称。对于一些非矩形阵列,并不满足以上条件,那么存在主瓣干扰时,传统的自适应波束形成算法的抗干扰性能下降,单
脉冲测角精度难以保持。
2 适用于非矩形阵列的自适应波束形成结构
本文提出的自适应波束形成信号处理架构如图4所示。与图1中传统的架构相比,我们在自适应波束形成前增加了对四个波束的线性补偿,并对已有的单脉冲查找表做线性校正。值得注意的是,下文中虽然该线性补偿因子是用一个划分为相同子阵的平面阵列推导得出的,但仍然可以推广到其他的非矩形二维阵列中。本文还证明该补偿因子只与阵列流形有关,且给出具体解析式。
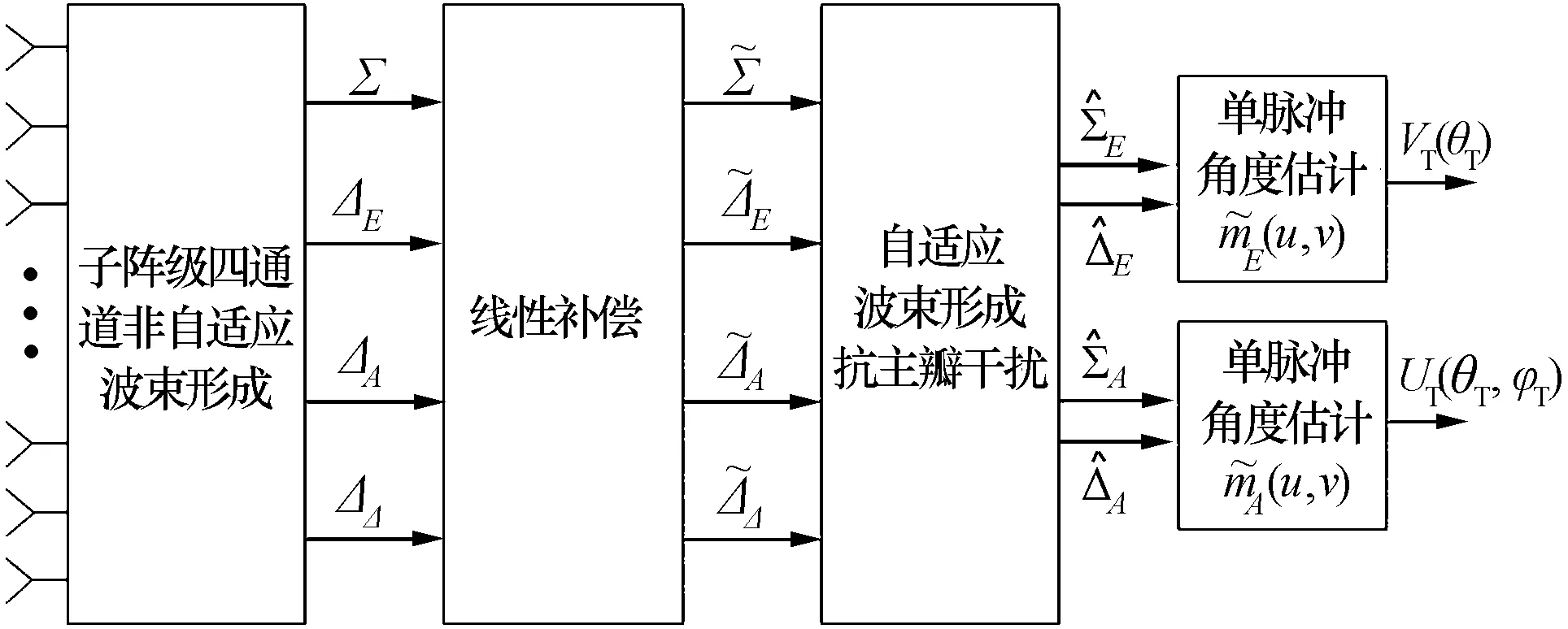
图4 适用于非矩形平面阵的自适应波束形成信号处理结构
2.1针对子阵形状相同的非矩形平面阵的线性补偿
假设一个二维平面阵,如图2b)所示,划分为12个相同子阵,每个子阵由nx×ny个阵元组成,阵元间距为半波长。该阵列的波束方向图可分别表示为
(12)
式中:fsub(u,v)表示每个子阵共有的和波束方向图;U表示位于整个阵列右上四分之一内子阵的序号集合。
将式(12)代入式(5)、式(6),单脉冲比可表示为
(13)
由于比幅单脉冲测角只用于主瓣内波束指向附近的目标,因此在上式中,u趋近于u0,v趋近于v0,所以有
(14)
将式(20)代入式(21),得到单脉冲比之间的关系如下
(15)
其中,
(16)
式中:|U|表示集合U中元素的个数。由式(16)可得,α仅与各子阵相位中心的坐标有关。
由式(15)和式(16),我们可以得出单脉冲比之间存在线性关系:在主瓣内,α趋近于一个常数。在此基础上,我们对非自适应波束输出的做线性补偿,并给出补偿后的波束方向图
(17)
将式(14)代入式(5)、式(6),可以得到
(18)
显然,除了式(17)给出的线性补偿方法以外,还有其他的补偿方法,比如
(19)
只要线性调整后的单脉冲比满足式(7)即可。
总的来说,上文中的线性补偿技术可以应用于任何平面阵。前提是该平面阵被划分为若干相同子阵,且各子阵关于x,y轴对称。实际中,出于子阵独立加权以形成低副瓣和差波束的考虑[8],的确存在许多雷达天线阵设计符合该要求。
2.2对其他非矩形平面阵线性补偿的推广
对于不符合上文要求的平面阵列流行,比如:
1) 圆面阵,如图2c):该阵列通常被划分为四个子阵,常用于四象限单脉冲雷达。值得注意的是,此处的四个子阵关于x,y轴对称,但并不相同。另外,在AMSAR[9]机载有源相控阵雷达的应用中,雷达拥有超过四个象限的通道。
2) 不规则子阵划分的平面阵:该阵列被划分为若干组子阵。不同组的子阵形状不同,同一组的子阵关于x,y轴对称,比如文献[10]中为避免栅瓣设计的二维通用阵列。
针对以上两种情况,可以将实际中的整个阵列概念上划分为广义的子阵——每个子阵仅含有一个阵元,而并不影响实际的子阵划分。此时,线性补偿因此可以定义为
(20)
式中:E表示在整个阵列右上四分之一内所有阵元的序号集合。
总的来说,本文给出的线性补偿方法与阵列流行、子阵数目、子阵形状无关。只要该非矩形平面天线阵列满足关于x,y轴对称的要求,那么在自适应数字波束合成中采用线性补偿法,即可同时完成抗主瓣干扰和对目标角度的精确估计。
3 仿真结果
下面给出本文提出的基于线性补偿法的自适应波束合成及目标测角算法应用于具体雷达天线阵列的仿真结果。设一个平面相控阵由12个相同的子阵组成,每个子阵含有8×8个阵元,排列成三角形栅格阵,间距均为半波长,如图2a)所示。雷达阵列的波束指向为(0°,0°)。没有幅度加权。首先形成四个非自适应的接收波束。可分别按式(5)、式(6)得出传统的单脉冲比,如图5a)和图5b)所示。
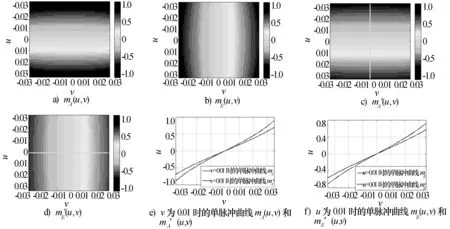
图5 基于图2b)中的非矩形平面阵,波束指向(0,0)
图5e)和图5f)分别给出了u或v为确定值时的单脉冲曲线。显然,此时单脉冲比并不相等,但在3dB主瓣内,十分接近线性关系。这就是我们做线性补偿的原因。按照式(6),计算得到α值为25/21,并对已有的单脉冲查找表作线性校正,校正后的单脉冲曲线如图6g)和图6h),此时近乎是同一条曲线。
假设目标的方位和俯仰角度为(-1°, -0.8°),用方向余弦表示为(-0.017 5, -0.014 0),信噪比为0dB。干扰的方位和俯仰角度为(1°, 0.6°),用方向余弦表示为(0.017 5, 0.010 5),从接收波束的主瓣进入天线,干噪比为30dB。做完线性补偿及自适应波束形成后,自适应单脉冲比如图6e)和图6f)所示,除了因主瓣干扰产生的自适应零陷,与原单脉冲比近似相同。
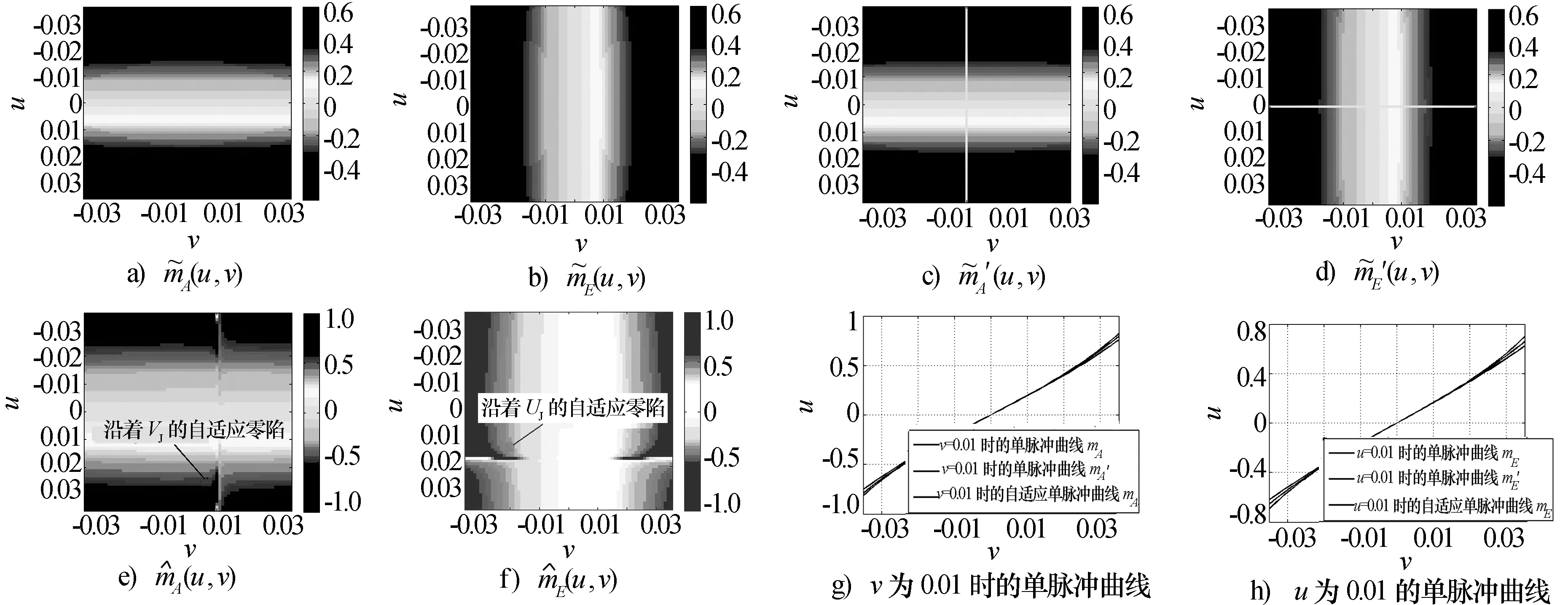
图6 基于图2b)中的非矩形平面阵,波束指向(0,0)时的单脉冲比对比图
下面分别用传统的方法和本文中提出的方法对目标的角度进行估计。进行100次相同条件下的仿真后,图7a)和图7b)给出了对应的结果。很显然,在主瓣干扰存在的情况下,本文提出的方法获得了更高的测角精度。

图7 SNR为0 dB,JNR为30 dB。基于图2b)中的非矩形平面阵,对目标角度多次估计的结果
4 结束语
在现代电子战中,雷达的干扰和抗干扰是一对永恒的矛盾。主瓣干扰是相控阵雷达常见的干扰形式之一,该干扰从天线的主瓣进入接收机,严重影响雷达系统的目标探测与跟踪性能。随着数字阵列信号处理技术的不断发展和在实际工程中的广泛应用,已有的数字波束形成系统可以同时合成四个高增益的接收波束,自适应的抑制主瓣干扰并对目标进行定位。而本文指出,已有的数字波束形成处理架构并不适用于所有的二维天线阵。尤其是对于非矩形二维阵列流形,利用现有的方法对目标进行角度估计的精度会大幅降低。因此,本文提出一种改进的自适应波束形成结构。首先,根据具体的阵列流形预先计算补偿因子,并对四个接收波束的输出做线性补偿;然后,进行自适应的主瓣干扰对消;最后,进行二维数字单脉冲测角。本文给出了相控阵雷达阵列的一个实例仿真结果,验证了新的方法相比于传统方法,在主瓣干扰存在时,对目标的测角精度有很大的提高。
[1]傅有光, 陈翼, 王宁. 现代机载雷达中抗干扰ECCM技术[J]. 现代雷达, 2014, 36(5): 1-5.
FUYouguang,CHENYi,WANGNing.Theanti-jammingECCMtechnologyofthemodernairborneradar[J].ModernRadar, 2014, 36(5): 1-5.
[2]段克清, 王永良, 谢文冲. 机载相控阵雷达抗压制性噪声干扰方法研究[J]. 现代雷达, 2009, 31(11): 81-85.
DUANKeqing,WangYongliang,XIEWenchong.Barragenoisejammingsuppressionmethodsforairbornephasedarrayradar[J].ModernRadar, 2009, 31(11): 81-85.
[3]FARINAA,GOLINOG,TIMMONERIL.Maximumlikelihoodestimatorapproachtodeterminethetargetangularco-ordinatesinpresenceofmainbeaminterference:applicationtolivedataacquiredwithamicrowavephasedarrayradar[C]//IEEEInternationalRadarConference. [S.l.]:IEEEPress, 2005: 61-66.
[4]WIDROWB,MANTEYP,GRIFFITHSL,etal.Adaptiveantennasystems[J].ProceedingsoftheIEEE, 1967, 55(12): 2143-2159.
[5]YUKB,MURROWDJ.Adaptivedigitalbeamformingforangleestimationinjamming[J].IEEETransactionsonAerospaceandElectronicSystems, 2001, 37(2): 508-523.
[6]ZHOUBL,LIRF,DAILY,etal.Combiningsum-differenceandauxiliarybeamadaptivemonopulsealgorithmatsubarraylevelforanti-jamming[C]//SignalProcessingInternationalConference. [S.l.]:IEEEPress, 2014: 277-282.
[7]NICKELU.Fundamentalsofsignalprocessingforphasedarrayradar[R].GAN-FHRResearchInstforHighFrequencyPhysicsandRadarTechniquesWachtberg,Germany, 2006.
[8]SHERMANSM.Monopulseprinciplesandtechniques[M].Norwood,MA,USA:ArtechHouse, 1985.
[9]CARLSONBD.Covariancematrixestimationerrorsanddiagonalloadinginadaptivearrays[J].IEEETransactionsonAerospaceandElectronicSystems, 1988, 24(4): 397-401.
[10]NICKELU.Monopulseestimationwithsubarray-adaptivearraysandarbitrarysumanddifferencebeams[J].IEEProceedingsofRadar,SonarandNavigation, 1996, 143(4): 232-238.
陈新竹女,1992年生,博士研究生。研究方向为雷达阵列信号处理,雷达抗干扰技术,雷达系统建模与仿真技术。
姜媛媛女,1983年生,工程师。研究方向为雷达总体技术,雷达抗干扰技术等。
舒汀男,1981年生,博士,讲师。研究方向为雷达与电子战射频仿真技术,实时信号处理系统设计与开发,相控阵雷达数字波束形成技术等。
郁文贤男,1964年生,博士,教授。研究方向雷达信号处理与目标识别技术,高分辨率SAR图像解译技术等。
AdaptiveMonopulseEstimationinMainlobeJammingforNon-rectangularPlanarArrays
CHENXinzhu1,JIANGYuanyuan2,SHUTing1,YUWenxian1
(1.ShanghaiKeyLaboratoryofIntelligentSensingandRecognition,ShanghaiJiaoTongUniversity,Shanghai200240,China) (2.ShanghaiAerospaceElectronicTechnologyInstitute,Shanghai201109,China)
Four-channelbeamsareformedsimultaneouslyinatypicaladaptivedigitalbeamforming(ADBF)architecturetocancelmainlobejammingandmaintainmonopulseangleestimationaccuracy.Forlargeantennaarrays,goodperformancehasbeenobtainedbyperformingdigitalbeamformingatsub-arrayoutputs.However,fornon-rectangulararrayconfiguration,theaccuracyofmonopulseangleestimationdecreasessothattheperformanceofthetypicalADBFseverelydegrades.Inthispaper,anoveladaptivebeamformingarchitectureisproposedfornon-rectangularplanararrays.First,linearcompensationisappliedtothefour-channelbeamoutputs,andthecompensationfactorisdetermineddirectlyfromthearrayconfiguration.Then,withthescaledmonopulseratiolook-uptables,thetwo-dimensionalanglesofthetargetareestimatedrespectively.Simulationresultofapracticalphased-arrayconfigurationvalidatestheeffectivenessofthenewmethod.
adaptivedigitalbeamforming;mainlobejamming;monopulseangleestimation;non-rectangularplanararray;linearcompensation
陈新竹Email:chenxinzhu@163.com
2016-01-15
2016-03-18
TN957
A
1004-7859(2016)06-0039-06
·信号处理·DOI:10.16592/j.cnki.1004-7859.2016.06.010

