混合粒子流滤波的非线性系统参数估计算法
赵知劲,吴 棫
(杭州电子科技大学 通信工程学院, 杭州 310018)
混合粒子流滤波的非线性系统参数估计算法
赵知劲,吴棫
(杭州电子科技大学 通信工程学院,杭州 310018)
为了提高强环境噪声下非线性系统估计性能,基于粒子流滤波对非线性系统估计能力强的特点,文中首先利用粒子流滤波粗估计状态向量;然后,利用卡尔曼滤波平滑由强环境噪声所导致的状态向量估计误差;最后,得到混合粒子流滤波算法。对转移方程为线性而测量方程为非线性的系统估计仿真实验表明:文中算法的参数估计精度高于普通粒子流滤波算法和粒子滤波算法,计算复杂度和普通粒子流滤波算法相当且低于粒子滤波算法。
粒子流滤波;卡尔曼滤波;粒子滤波;计算复杂度;估计精度
0 引 言
近年来非线性滤波算法在信号处理、目标跟踪及数据融合等领域的应用已引起越来越多研究者的关注[1]。传统的非线性滤波方法主要有扩展卡尔曼滤波算法(EKF)[2]和无迹卡尔曼滤波算法(UKF)[2],这两种方法仅适用于估计弱非线性系统模型情况。当系统模型非线性程度较强时,EKF和UKF的估计误差较大且可能发散。基于贝叶斯法则的粒子滤波算法(PF)[3]适用于估计强非线性系统模型,当粒子数足够多时,该方法能够得到较好的估计结果。但是粒子滤波存在难以选取重要性分布函数、粒子贫化[4]以及由粒子数增加导致计算复杂度高等问题。针对粒子滤波存在的问题,文献[5]提出了一种新的粒子型滤波算法——粒子流滤波算法(PFF),用于估计非线性系统。PFF用粒子流方法替换PF中的重采样方法,从而避免了重采样带来的粒子贫化和计算量增加问题。
针对由线性转移方程和非线性测量方程组成系统的估计问题,本文提出一种由EKF和PFF结合的改进算法,即混合粒子流滤波算法(HPFF)。HPFF的计算复杂度和PFF相当且低于PF,但其估计精度高于PFF和PF。
本文详细介绍了粒子流滤波算法,对提出的混合粒子流滤波算法进行了描述,并通过对所提算法进行计算机仿真实验,与其他算法性能进行了结果比较。
1 混合粒子流滤波算法
利用粒子流滤波算法解决估计问题时,建立动态系统的状态空间模型。本文研究的动态系统状态模型如下
Xk=SXk-1+uk-1
(1)
yk=h(Xk)+vk
(2)
式中:Xk∈Rm为k时刻m维状态向量;S∈Rm×m为已知的状态转移矩阵;uk为均值为0、方差为Q的高斯分布状态噪声;yk为k时刻的测量值;h(·)为关于Xk的线性或非线性测量函数;vk为均值为0、方差为σ2的高斯分布环境噪声,且vk与uk统计独立。
利用贝叶斯法则可以得到状态向量Xk的概率密
度函数如下
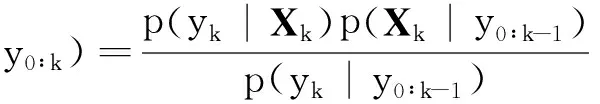
(3)
式中:y0∶k为时刻0到时刻k所有的测量值;p(Xk|y0∶k)为后验概率密度;p(yk|Xk)为似然函数;p(Xk|y0∶k-1)为先验概率密度;p(yk|y0∶k-1)为与状态向量Xk无关的归一化常数。后验概率密度包含了对状态向量Xk估计的全部信息,利用后验概率密度可以完成对状态向量Xk的估计,但是由于后验概率密度表达式复杂,难以直接计算其结果。
粒子滤波利用更新粒子的权值以及重要性采样方法来表征后验概率密度实现贝叶斯估计;而粒子流滤波则是通过将粒子平滑移动到状态空间的后验分布上实现贝叶斯估计。图1给出了粒子滤波和粒子流滤波过程的形象化描述,上半部分虚线框图描述了粒子滤波过程,下半部分虚线框图描述了粒子流滤波过程。
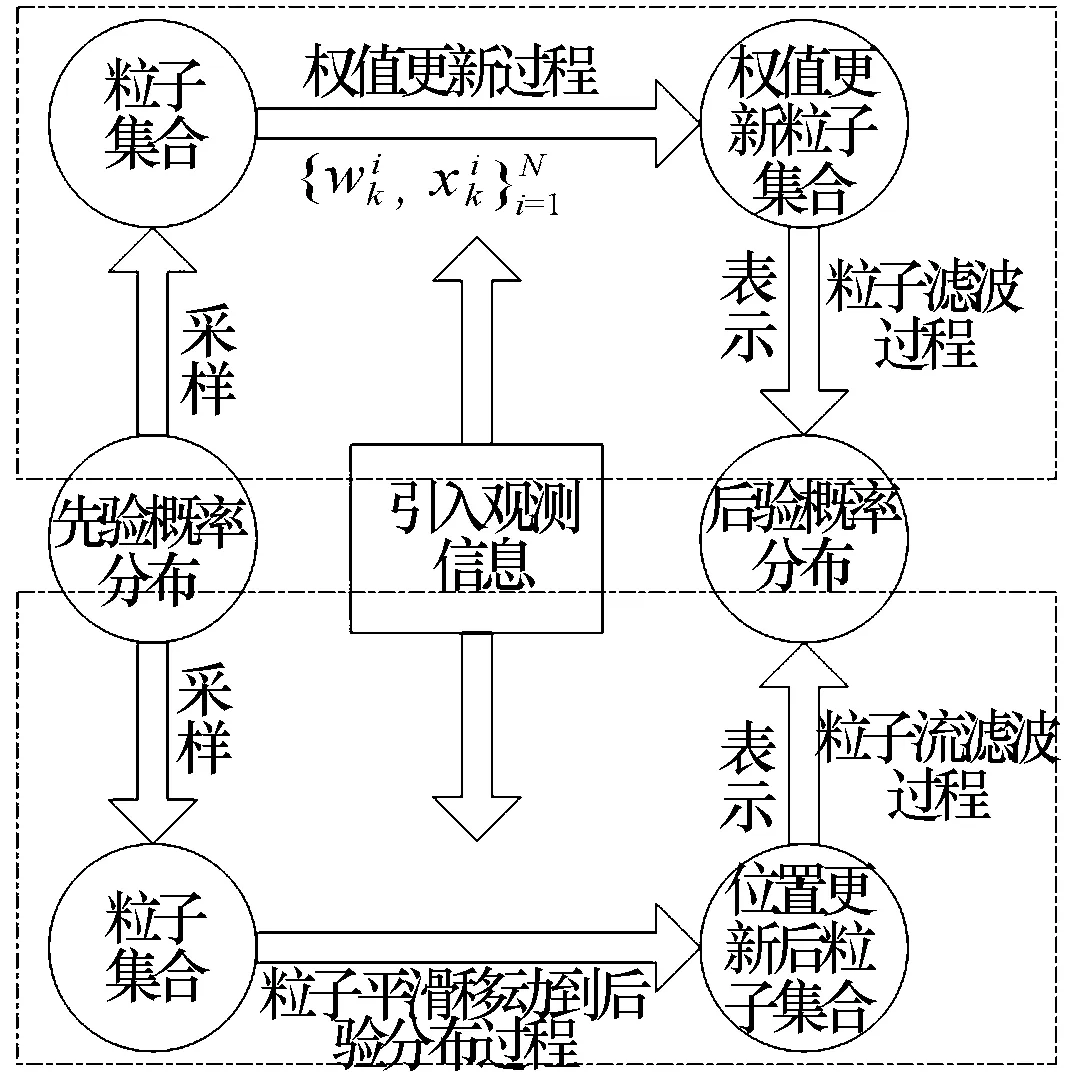
图1 粒子滤波与粒子流滤波框架图比较
为方便起见,将式(3)中的有关函数简化表示如下:q(X)=p(Xk|y0∶k),g(X)=p(yk|Xk),I(X)=p(Xk|y0∶k-1)。利用式(3)和拓扑学中同伦函数[6]的概念定义一个针对变量λ的条件概率密度对数流如下
logq(X,λ)=logg(X)+λlogI(X)+K(λ)
(4)
式中:λ为数值从0变化到1的参数,此处为类似于时间的变量;q(X,λ)为X的条件概率密度,其中,X为关于λ的函数;K(λ)为与X无关的归一化常数。当λ=0时,q(X,λ)表示先验概率密度;而当λ=1时,q(X,λ)表示后验概率密度,这正是我们希望得到的结果。由于状态向量X为关于λ的函数,我们定义状态向量X对于变量λ的变化率为
(5)
f(X,λ)的物理意义可以解释为:若状态向量X为状态空间Rm中的某一点,那么f(X,λ)就是该点在λ时刻的速度。由于变化率f(X,λ)在所有粒子上都有定义,可以认为f(X,λ)定义了一个从先验分布到后验分布的“速度场”。求得f(X,λ)之后即可利用数值积分将先验粒子平滑移动到后验分布上,从而实现粒子更新。
假设f(X,λ)满足零散度的Fokker-Planck方程[7],且由文献[8]可得
(6)
式中:Tr(·)为(·)的迹。因为q关于λ是光滑和连续的,式(4)两端同时对λ求导可得
(7)
结合式(6)和式(7)可以得到以下等式
(8)
式(8)就是式(3)贝叶斯估计所应满足的常微分方程。求解式(8)得到f(X,λ),然后对f(X,λ)进行数值积分就能得到所要估计的X,这就是粒子流滤波。式(8)有多种求解方法[9-10],如准无旋近似法、变分近似法和参数近似法等。文献[11]给出了一种利用参量近似求解式(8)的方法,该方法将先验分布和似然分布都近似成高斯分布,并且利用一阶泰勒级数近似测量函数h(·),得到了一种易于计算和编程实现的封闭形式解。
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
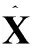
(17)
(18)
(19)
(20)
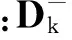
p(X0)=U(α,β)
(21)
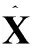
(22)
综上所述,混合粒子流滤波算法的具体步骤如下:

(2)fork = 1,2,…,T
(5)forj = 1,2,…,Nλ
(6)将λ的值设为:λ=jΔλ
(8)利用式(10)和式(11)计算A(λ)和b(λ)
(9)fori = 1,2,…,N
(12)endi
(14)endj
(15)利用式(12)~式(14)对Pk-1更新得到Pk
(18)endk
2 算法仿真与性能分析
本节分析比较了PF、混合粒子滤波(MPF)[12]、PFF和HPFF四种算法对正弦信号参数的估计性能。所用软件为Matlab2010b版本,在Intel酷睿双核处理器(2.13GHz)、2GB内存的PC机上进行仿真实验。将含有未知参数的正弦信号用如下状态模型表示
(23)
yk=αkcos(2πftk+φk)+vk
(24)
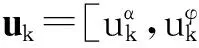
PF、MPF、PFF和HPFF四种算法估计得到的信号幅度和相位参数如图2所示。由图2可见,四种算法均能逐渐收敛于待估计向量Xk的真实值,由于HPFF算法是PFF算法估计结果再经KF滤波得到的。因此,与其他三种算法相比,HPFF的估计结果更加稳定。

图2 参数估计结果
(25)
用式(25)定义的均方根误差来比较分析四种算法的性能。100次独立仿真实验,即K=100,四种算法对两个未知参数估计的均方根误差随采样点数的变化曲线如图3所示。随着采样点数的增加,四种算法的均方根误差都随之减少并趋于稳定值,HPFF的估计均方根误差最小,MPF次之,PFF再次之,PF最大。

图3 4种算法的均方根误差
环境噪声方差取50、100、150、200、250和300时,四种算法对两个未知参数估计的均方根误差如图4所示。HPFF算法的均方根误差比其他三种算法小得多,四种算法的均方根误差随着噪声方差的增加而增加。
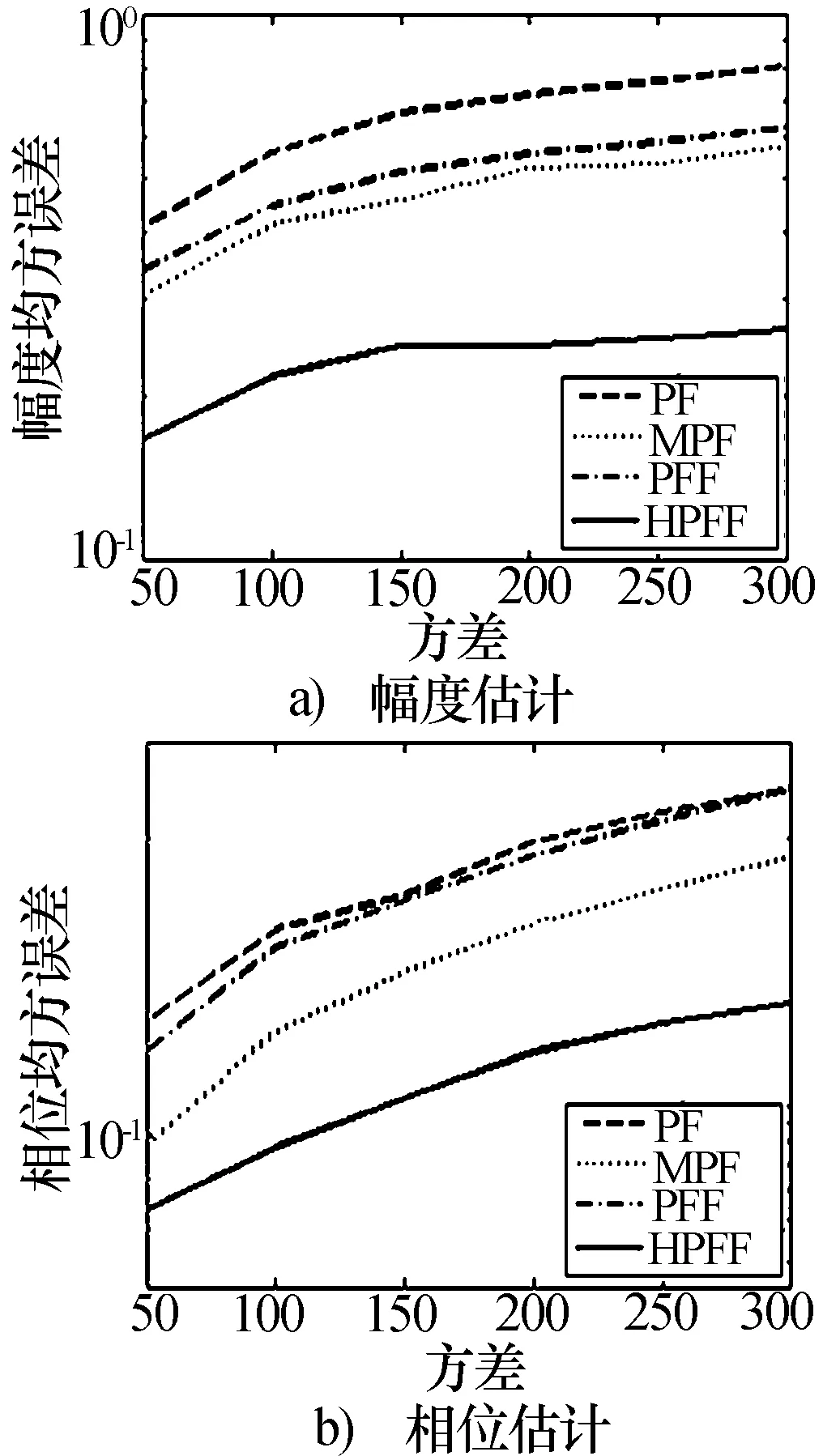
图4 不同环境噪声下仿真结果
粒子数取20、50、100、200和500时,PFF和HPFF对两个未知参数估计的均方根误差如图5所示。不同粒子数下,HPFF的均方根误差都小于PFF;并且HPFF和PFF受粒子数的影响较小,当粒子数大于100时HPFF和PFF估计精度趋于稳定。
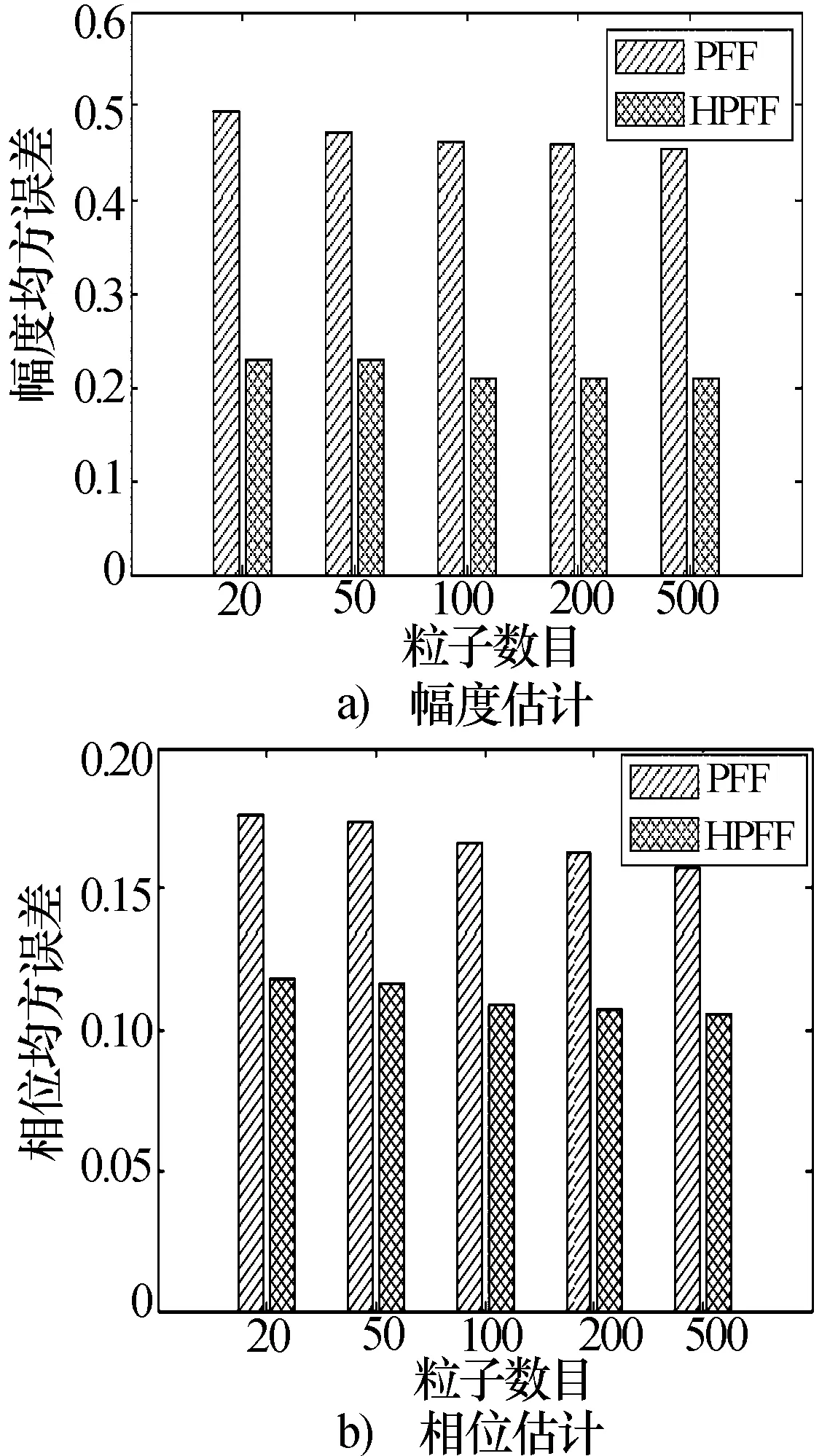
图5 不同粒子数目下仿真结果
由于算法的计算复杂度随着粒子数的增加而增加,选取100作为PFF和HPFF的粒子数,每种滤波算法分别进行100次仿真实验,四种算法的运行时间平均值如表1所示。PFF算法运行速度最快,HPFF速度接近于PFF,比MPF和PF快得多。
表1四种滤波算法的平均运行时间s

滤波算法名称运行时间PF81.7513MPF83.1928PFF26.4282HPFF28.0834
3 结束语
本文提出的混合粒子流滤波算法首先利用粒子流滤波得到一个粗估计结果,然后在粗估计结果基础上利用卡尔曼滤波进一步平滑滤波得到最终估计结果。对转移方程为线性而测量方程为非线性的系统模型估计仿真结果表明:HPFF算法是有效的;在强环境噪声背景下,HPFF算法的估计精度高于PF、MPF和PFF;HPFF和PFF的算法复杂度相当,低于PF和MPF算法。
[1]DAUMF.Nonlinearfilters:beyondtheKalmanfilter[J].IEEEAerospaceandElectronicSystemsMagazine, 2005, 20(8):57-69.
[2]SIMOND.Optimalstateestimation:Kalman,Hinfinity,andnonlinearapproaches[M].Hoboken:JohnWiley&Sons, 2006.
[3]康健, 司锡才, 芮国胜. 基于贝叶斯原理的粒子滤波技术概述[J]. 现代雷达, 2004, 26(1): 34-36.
KANGJian,SIXicai,RUIGuosheng.ParticlefilteringtechniquesbasedonBayesiantheorem[J].ModernRadar, 2004, 26(1): 34-36.
[4]DAUMF,HUANGJ.Particledegeneracy:rootcauseandsolution[C]//InternationalSocietyforOpticsandPhotonics,Defense,Security,andSensing.Florida:SPIEPress, 2011: 1-11.
[5]DAUMF,HUANGJ.Particleflowfornonlinearfilters,Bayesiandecisionsandtransport[C]// 2003 16thInternationalConferenceonInformationFusion(FUSION).Istanbul:IEEEPress, 2013:1072-1079.
[6]WHITEHEADGW.Elementsofhomotopytheory[M].Massachusetts:Springer, 2012.
[7]RISKENH.TheFokker-Planckequation:methodsofsolutionandapplication[M].Berlin:Springer, 1996.
[8]DAUMF,HUANGJ.Exactparticleflowfornonlinearfilters:seventeendubioussolutionstoafirstorderlinearunderdeterminedPDE[C]// 2010ConferenceRecordoftheFortyFourthAsilomarConferenceonSignals,SystemsandComputers.PacificGrove,CA:IEEEPress, 2010: 64-71.
[9]DAUMF,HUANGJ.Particleflowfornonlinearfilters[C]//2011IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing(ICASSP).Prague:IEEEPress, 2011: 5920-5923.
[10]DAUMFE.Exactfinite-dimensionalnonlinearfilters[J].IEEETransactionsonAutomaticControl, 1986, 31(7): 616-622.
[11]DINGT,COATESMJ.ImplementationoftheDaum-Huangexact-flowparticlefilter[C]// 2012IEEEStatisticalSignalProcessingWorkshop(SSP).AnnArbor,MI:IEEEPress, 2012: 257-260.
[12]夏楠, 邱天爽, 李景春, 等. 一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J]. 电子学报, 2013, 41(1): 148-152.
XIANan,QIUTianshuang,LIJingchun,etal.AnonlinearfilteringalgorithmcombiningtheKalmanfilterandtheparticlefilter[J].ActaElectronicaSinica, 2013, 41(1): 148-152.
赵知劲女,1959年生,教授,博士生导师。研究方向为通信信号处理、自适应信号处理、认知无线电等。
吴棫 男,1991年生,硕士研究生。研究方向为信号与信息处理。
ANonlinearSystemParameter'sEstimationAlgorithmBasedonHybridParticleFlowFilter
ZHAOZhijin,WUYu
(SchoolofCommunicationEngineering,HangzhouDianziUniversity,Hangzhou310018,China)
Inordertoimproveestimationperformanceofthenonlinearsystemunderstrongenvironmentalnoise,thestatevectorisroughlyestimatedbyparticleflowfilterfirstlysinceitisgoodforhandlingnonlinearsystemestimationproblem.Thenthestatevector'sestimationerror,whichiscausedbythestrongenvironmentnoise,issmoothedbyaKalmanfilter.Finallythehybridparticleflowfilterisgotten.Theresultsofsimulationforthesystemestimationconsistingoflineartransferequationandnonlinearmeasurementequationshowthattheestimationaccuracyoftheproposedalgorithmishigherthanthatofthestandardparticleflowfilterandtheparticlefilter,computationalcomplexityofproposedalgorithmisthesameasstandardparticleflowfilterandislowerthanthatoftheparticlefilter.
particleflowfilter;Kalmanfilter;particlefilter;computationalcomplexity;estimationaccuracy
吴棫Email:waynegeek@yeah.net
2016-01-22
2016-03-20
TN911
A
1004-7859(2016)06-0045-05
·数据处理·DOI:10.16592/j.cnki.1004-7859.2016.06.011

