基于数字滤波器的频率响应仿真实验平台

付　莉, 高兴泉

(吉林化工学院 信息与控制工程学院, 吉林 吉林　132022 )



基于数字滤波器的频率响应仿真实验平台

付莉, 高兴泉

(吉林化工学院 信息与控制工程学院, 吉林 吉林132022 )

为提高电子技术中关于频率响应的教学质量,提出一种基于DSP Builder/Matlab的滤波器仿真实验平台设计方法。以IIR数字滤波器为例,利用DSP Builder模块搭建图形化IIR滤波器模型,利用Matlab程序化设计IIR数字滤波器,分别仿真验证滤波器功能、对比校验实验效果。该仿真实验平台将电子技术、数字信号处理、EDA技术联系起来,实现简单，效果生动、形象,有利于学生理解和掌握相关理论知识。

频率响应； 数字滤波器； DSP Builder/Matlab； 实验平台

频率响应是电子技术中非常重要但较难理解的专业知识,理论分析十分抽象,学生在进行频率响应实物验证实验及电路设计时会感到困难[1-2]。本文以IIR(infinite impulse response,无限冲激响应)数字滤波器为例,介绍利用DSP Builder软件建立图形化模型仿真滤波器的方法,并以单位阶跃响应为输入信号,仿真滤波效果,同时利用Matlab滤波器工具箱FDATool(filter design and analysis tool)和Matlab程序分别进行仿真验证,对比图形化模型仿真的正确性[3]。

1　滤波器系统原理

滤波是从原始信号中得到目标信息的过程,在此过程中需消除或减小噪声。滤波器应具有一定传输特性和频率响应。根据处理信号的不同,滤波器有两类——数字滤波器和模拟滤波器。由于数字滤波器具有高精度、高可靠性、灵活性强、并行处理等优点,它被广泛应用于自动控制、地质勘探、图像处理、数字通信等领域[4-5]。

数字滤波器有两种:IIR滤波器和FIR(finite impulse response,有限冲击响应)滤波器[6]。数字滤波器在频域中利用系统函数或频率响应描述。

数字滤波器频率响应描述为

(1)

IIR数字滤波器的优点在于较高的频率只需低阶数,幅频特性较好、占用存储单元少、效率高、计算量小。IIR无限长单位脉冲响应滤波器的差分方程如下[8]:

(2)

IIR滤波器系统函数表示为

(3)

由式(3)可导出IIR滤波器直接I型(式(4))和直接II型(式(5)):

(4)

(5)

相对于直接I型,直接II型减少了M个延时环节,若M=N,结构中延时部分缩减了一半,软件和硬件均节省了存储单元和寄存器。另外,由式(3)进行因式分解,可得:

(6)

式(6)中,b1i,b2i,b3i均为实数,将(1-b1i)和(1-a1i)作为1+b2iz-1+b3iz-2和1+a2iz-1+a3iz-2系数为零的二阶因子,可转换为公式(7)。对于Hi(Z)是一个二阶IIR滤波器,也可以认为N阶滤波器则是由多个二阶IIR滤波器级联构成。这种形式可准确传输零点[9]。

(7)

2　滤波器仿真实验平台实现

根据IIR滤波器原理分析,该滤波器可以利用Simulink图形化环境DSP Builder软件平台实现,同时借助Matlab较强的计算能力,可方便地设计数字滤波器。该图形化仿真平台生动形象,可方便观察、分析信号通过滤波器后表现出的频率响应,辅助学生对知识的理解。

2.1DSP Builder仿真实现

DSP Builder是一种图形化编辑软件,支持硬件设计,系统和算法共享一个公共开发平台[10]。设计者可以通过其模块生成系统模型,仿真验证后可与硬件相连,下载到FPGA硬件中直接测试,便于调试、应用灵活。

根据IIR数字滤波器工作原理,本文利用该滤波器的级联型和直接II型设计一种高通滤波器,说明信号通过滤波器后的频率响应。以简易的四阶IIR滤波器为例,滤波器类型为高通滤波器HighPass,设定采样频率fs=48 MHz,截止频率fc=10.8 MHz,设计方法类型为巴特沃思(Butterworth)。

在模型化的搭建中,IIR滤波器存在增益和滤波系数的计算,借助于FDATool计算滤波器系数,联合DSP Builder工具箱中模块建立模型,仿真实现设定的滤波器。打开FDATool工具箱[11],根据滤波器类型、采样频率、截止频率设置参数,设置滤波器后生成模型,在界面中可以观察出相应的幅频特性和相频特性。如图1所示。

图1　幅频特性和相频特性

在频率响应曲线中可看到幅值和相位变化。当频率大于10.8 MHz后幅值分贝接近于0,同时对应的相位偏移相对较少,数字信号失真小,满足设计要求。观察频率响应后导出滤波器系数G和SOS矩阵[12-13],递归型线性时不变的因果系统结构利用DSP Builder软件平台，可成功搭建出级联型四阶IIR滤波器,图形化模块中添加G和SOS值,四阶级联型结构分成2个二阶形式,每阶有2个反馈环节,利用延时单元连接而成。级联型[14]IIR滤波器模型如图2所示。

图2　级联型IIR滤波器模型

为了模拟干扰信号通过滤波器后的状态,本系统输入端引入阶跃响应,通过Simulink工具箱中Scope模块观察滤波效果。对于IIR的另一种类型直接II型,同样可以搭建模型,系统参数可以利用Matlab语言[B,A]=sos2tf(SOS,G)转换生成,然后根据系统结构形成图形化模型,直接II型滤波器模型如图3所示。

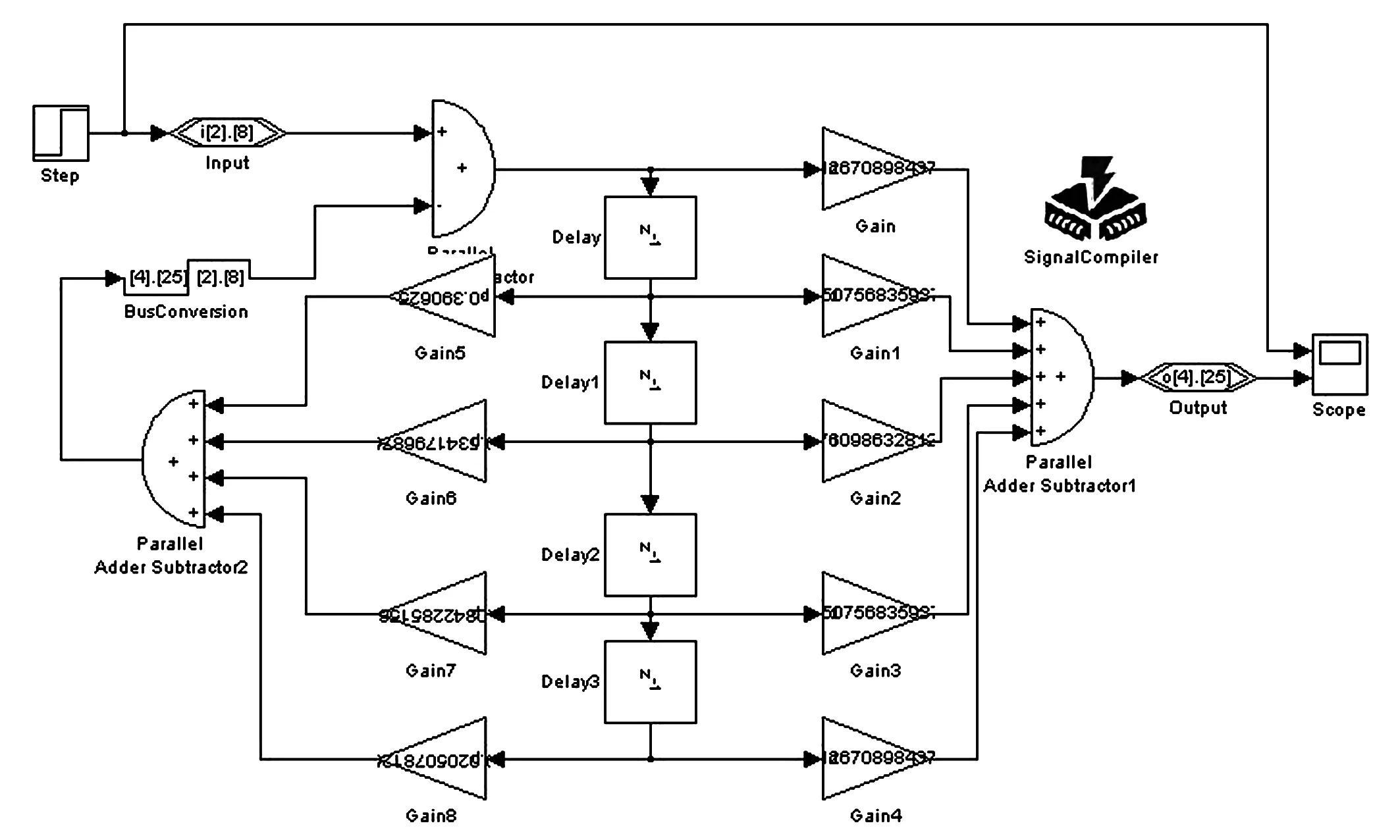
图3　直接II型IIR滤波器模型

阶跃模块的阶跃时间设定为10-7s,仿真时间为10-6s。系统仿真图如图4所示。由图4观察到0.4×10-6s后系统基本稳定，没有跃变。

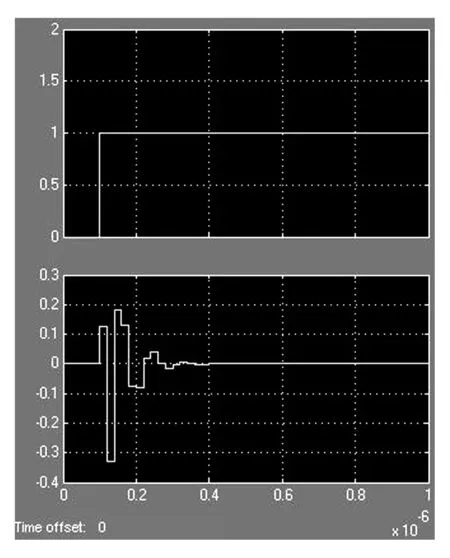
图4　IIR滤波器DSP Builder阶跃响应系统仿真

2.2Matlab程序化仿真实现

由于学生在大一期间学习过Matlab课程,在学习频率响应内容时可利用Matlab,根据滤波器工具FDATool导出系数,利用Matlab语言实现采样频率fs=48 MHz和截止频率fc=10.8 MHz的高通滤波器,并对其进行阶跃响应仿真,观察滤波效果。

在Matlab的信号处理工具箱中,IIR滤波可以利用sosfilt函数实现。sosfilt函数可实现信号通过滤波器后获得有效输出信号,具体程序如下:

y1=filter(B,A,x);

y2=sosfilt(SOS,x);

subplot(211),

stem(n,y1,′lineWidth′,2);

xlabel(′n′);ylabel(′y1(n)′);

grid;

title(′函数filter求出的阶跃响应′);

axis([-1 21 -1 1]);

subplot(212);

subplot(212),

stem(n,y2,′LineWidth′,2);

xlabel(′n′);ylabel(′y2(n)′);

grid;

title(′函数sosfilt求出的阶跃响应′);

axis([-1 21 -1 1]);

程序中分别调用函数filter和sosfilt对级联型和直接II型滤波器进行仿真验证,程序运行后得到系统仿真如图5所示。

图5　Matlab阶跃响应系统仿真图

另外,作为系统在单位阶跃信号激励下产生零状态的阶跃响应,在FDATool的分析部分中可分析。该高通滤波器的阶跃响应如图6所示。

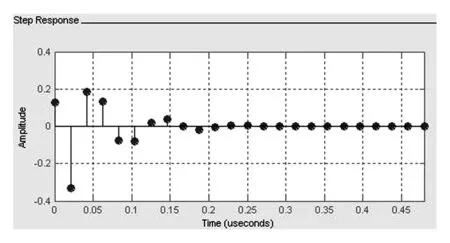
图6　FDATool阶跃相应仿真图

通过DSP Builder图形化模型、Matlab程序化语言以及FDATool滤波器工具分别对IIR滤波器实现阶跃响应,通过对仿真波形依次对比,可观察到3种仿真波形完全相同。学生可以利用更轻松和直观的图形模型学习难理解的课程内容,同时根据之前学过的内容来验证新的实验方法的正确性。多元化实验方法更好地拓展了学生的思维和创新性。

3　结语

以IIR数字滤波器在DSP Builder仿真平台建模实现为例,对理解难度较大的频率响应教学内容,生动形象地展示了其特性和应用性,同时结合Matlab滤波器工具箱和语言编辑,共同验证图形化模型的正确性。把理论知识、EDA技术和实践工程技术融为一体,深化了学生对理论知识的理解,拓展了学生思维,提升了学生探索实践能力。该系统采用模块化搭接,形式简单、灵活、易实现,仿真后可直接下载硬件实现,为学生进行硬件实验打下基础,也提高了实验教学效率。

References)

[1] 闫俊荣,崔霞,张彩荣.滤波器的频率特性仿真实验研究[J].实验技术与管理,2012,29(1):86-87.

[2] 刘艳,朱昌平,宋凤琴,等.模拟电子技术实验教学中的学生实践能力培养[J].实验技术与管理,2010,27(2):110-112.

[3] 晏湧.模拟电子技术实验教学改革的探索与实践[J].实验技术与管理,2012,29(4):288-289.

[4] 刘彩霞.数字滤波器的设计[D].哈尔滨:哈尔滨工程大学,2007:1-20.

[5] Matsunaga T,Yoshida M,Ikehara M. Design of IIR digital filters in the complex domain by transforming the desired response[J]. IEEE Transactions on Signal Processing, 2004,52(7):1975-1982.

[6] 潘晓东.数字分频与扬声器管理系统[J].演艺设备与科技,2008(6):15-19.

[7] 王彬,于丹,汪洋.MATLAB信号处理[M].北京:机械工业出版社,2010:142-170.

[8] 董应平.IIR数字滤波器优化设计及FPGA仿真验证[D].成都:西南交通大学,2009:5-16.

[9] 屈星,唐宁,严舒,等.基于FPGA的IIR数字滤波器的设计与仿真[J].计算机仿真,2009,26(8):304-307.

[10] 付莉,高兴泉.基于DSP Builder的电子技术仿真实验平台[J].实验技术与管理,2015,32(1):134-137.

[11] 赵瑞堃.基于MATLAB的FIR和IIR数字滤波器的设计[D].长春:吉林大学,2012:31-38.

[12] 姜乃卓,都恩丹.IIR数字滤波器的系数量化效应分析[J].电子测量技术,2010,33(12):8-11.

[13] 刘彬.MATLAB环境下IIR滤波器设计、仿真与验证[J].电子测量技术,2011,34(4):7-10.

[14] 潘松,黄继业,王国栋.现代DSP技术[M].西安:西安电子科技大学出版社,2003:187-203.

Simulation experimental platform for frequency response based on digital filter

Fu Li, Gao Xingquan

(College of Information & Control Engineering, Jilin Institute of Chemical Technology, Jilin 132022, China)

In order to solve the problems with abstract of frequency response of electronic technology teaching content, difficult to understand, insufficient of hardware resources, a kind of simulation experimental platforms based on DSP Builder/Matlab is proposed. Taking the infinite impulse response digital filter as an example, the working principle of infinite impulse response is introduced, and a graphical model of the IIR filter is built by using of DSP Builder module. In addition, the design of IIR filter is realized by use of Matlab programming, the simulation result of which is contrasted with the one of DSP Builder module, and the function of filter is verified. Electronic technology, digital signal processing and EDA technology are integrated by this simulation experimental platform. It is easy to realize and the simulating effect is vivid. With the help of simulation experiment, the students’ understanding theory knowledge and analytical skills will be improved largely.

frequency response; digital filter; DSP Builder/Matlab;experimental platform

DOI:10.16791/j.cnki.sjg.2016.04.033

2015- 09- 10

吉林省教育厅项目(20140352)；吉林市科技计划项目(201212208)

付莉(1985—),女,吉林省吉林市,硕士,讲师,主要研究方向为EDA技术及电子技术.

E-mail：fuli247012412@126.com

TN713

A

1002-4956(2016)4- 0119- 04