中国产业结构整体同构化趋势研究——基于成分数据统计

胡玉琴 ，薛留根

(1.北京工业大学 应用数理学院, 北京 100124；2.浙江财经大学 数据科学学院， 浙江 杭州 310018)



中国产业结构整体同构化趋势研究
——基于成分数据统计

胡玉琴1,2，薛留根1

(1.北京工业大学 应用数理学院, 北京 100124；2.浙江财经大学 数据科学学院， 浙江 杭州 310018)

已有产业结构同构化指标适用于两两地区之间的同构化测度，缺乏从整体角度提出多个地区的测度方法。运用成分数据统计理论，在三元图直观反映产业结构整体演变的基础上，提出结构中心和结构离散度指标来整体测度产业结构同构化，并对中国31个省份以及东部、中部、西部和东北地区不同区域的产业结构同构化进行实证分析。研究表明：中国31个省份整体同构化程度比较稳定，东部区域同构化程度最低，而不同区域则呈现出不同的同构化趋势。

产业结构；整体同构化；成分数据统计；结构中心；结构离散度

一、引 言

区域产业结构同构化是各个区域的产业结构在动态演变进程中所呈现的一种共同发展倾向，是经济发展过程中的一种客观现象。如何正确对待区域产业结构同构化，直接影响着区域产业政策的制定和协调发展战略的实施，因而区域产业结构同构化问题引起了国内外学术界和各级政府部门的关注。合理刻画区域产业结构同构化的程度并把握区域产业结构同构化的趋势，即区域产业结构同构化程度的度量问题，一直是区域经济研究的热点。

关于测度区域产业结构同构化指标的研究成果并不多，目前主要有结构相似系数、结构差异度指数、结构重合度指数以及产业熵指数等指标[1-4]。大量文献研究主要集中在运用上述指标分析具体区域或具体产业结构内部的产业结构同构化[5-7]。由于上述指标均反映两个具体地区之间的同构化程度，因而应用到反映包括多个地区(多于两个)的区域产业结构整体同构化的研究中主要通过以下两种途径得到实现。其一是通过分别测度区域内部两两地区的上述指标，用指标的平均值来反映区域产业同构化程度[6,8]；其二是首先选择某一地区作为基准，然后测度区域的每个地区与基准之间的上述指标，从而用指标的平均值反映区域产业结构同构化[7]。目前仍缺乏整体测度区域产业结构同构化指标的研究，因而缺乏对中国的整体性研究。本文试图构建测度产业结构整体同构化的指标，并对中国三次产业的产业结构同构化进行研究。

从数学的角度，可把同一时刻区域中每个地区的产业结构看作是对应维度向量空间的向量，结构相似系数的本质是向量间的夹角余弦[2]，结构差异度指数和重合度指数可视为向量间某种距离的形式，即借助反映向量间的夹角或距离来衡量产业结构的同构化。由于每个地区产业结构不同，因而产业结构向量呈现出变异性，从统计的观点可通过方差或标准差反映产业结构的变异程度即同构化。然而产业结构本质上是成分数据，受到定和条件的约束，传统统计分析方法不能直接实施，应采用成分数据统计进行分析[9-12][13]15-16。目前，成分数据统计在产业结构中已有一定的运用，但仅停留在产业结构的预测，尚未对产业结构同构化问题进行讨论[14-15]。

本文基于成分数据统计理论，提出一种整体测度产业结构同构化的指标，并对中国的产业结构整体同构化进行实证分析。

二、成分数据统计基础

(一)单形空间和Aitchison几何

对于三元成分数据x=(x1,x2,x3)满足的空间：

S3={(x1,x2,x3)|xi>0,i=1,2,3;x1+x2+x3=1}

(1)

称为三维单形空间(simplexspace)[10]。由于本文考虑三次产业所占比重所构成的产业结构是三元成分数据，因而以三元成分数据为主来介绍。

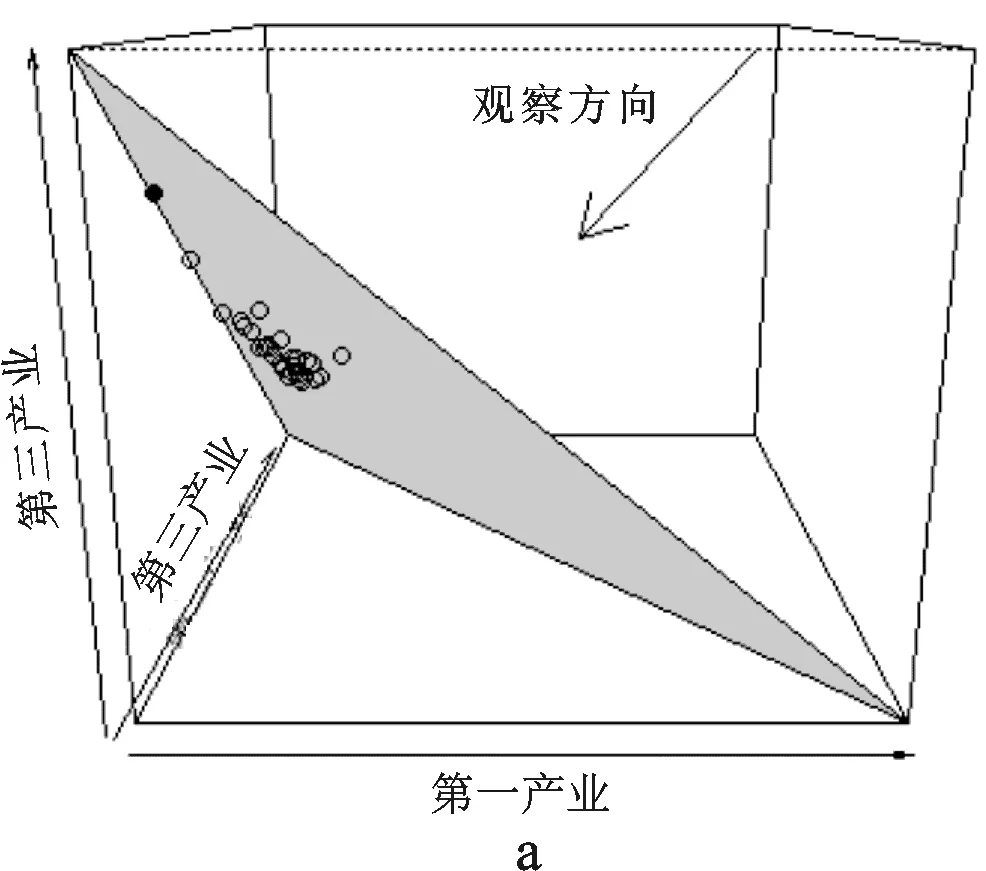
图1　2013年中国31个省份产业结构三维透视图和三元图

图1a图是2013年中国31个省份产业结构数据所呈现的三维透视图，每个省份的产业结构在三维空间中表示成1个点，即三维向量。由于产业结构各分量xi>0，且受到定和条件1的限制，产业结构数据不能在三维欧式空间中自由取值，基于观察方向，产业结构数据在一个由坐标(1,0,0)、(0,1,0)和(0,0,1)组成的三角形区域取值，即三维单形空间，可用三元图(ternarydiagram)来表示，见图1b图。本文中所有图借助统计软件R中的compositions包来实现。三元图点的坐标根据点到对应边的垂直距离来确定[10]。以实心点表示2013年北京市产业结构数据(0.008,0.223,0.769)，在三元图中该点到由第二产业和第三产业所在边的垂直距离0.008表示其第一产业比重，该点到第一产业和第三产业所在边的距离0.223表示其第二产业比重，该点到第一产业和第二产业所在边的距离0.769表示其第三产业比重。三元图反映2013年中国31个省份以第二产业或第三产业为主导，其中第二产业为主导的省份占多数。

与欧式空间不同，单形空间的成分数据有着自身的几何。在遵循成分数据子成分不变性等原则下，Aitchison引入闭合运算定义了类似欧式空间的向量加法和数乘，并定义成分数据的距离等构建Aitchison几何的基本框架[9]；Egozcue等提出单形空间中基和坐标的概念，Aitchison几何已成为成分数据分析的基础[12]。在闭合运算(closureoperation)C(·)的作用下，对于三维单形空间S3的任意两个向量x,y，以及任意实数a，定义成分数据的加法(perturbation operation)：

x⊕y=C(x1y1,x2y2,x3y3)

(2)

数乘(power transformation)*可译为扰动算子和幂变换，这里的翻译主要是与欧式空间向量运算的加法和数乘相对应，以便于理解。：

α⊗x=C(x1α,x2α,x3α)

(3)

距离(Aitchison distance)：

(4)

由于Aitchison几何呈现的向量关系与经典欧氏空间的欧式几何不存在一致性[12]，因而直接运用欧式几何的向量关系处理成分数据是不恰当的，结果会做出不可靠甚至扭曲的判断[16]。

(二)对数比变换

成分数据统计的基本原则是借助对数比变换来实现Aitchison几何向欧式几何的转换，从而进行经典的统计分析。常用的对数比变换有alr变换(additivelogratiotransformation)和clr变换(centeredlogratiotransformation)以及ilr变换(isomtriclogratiotransformation)[9-12]。上述三种变换均为一一对应的变换。

由于clr变换和ilr变换具有度量不变性的特点，即对成分数据进行clr或者ilr变换所得的数据，可以直接使用欧式几何进行度量，而alr变换不具有此性质，再则ilr变换实际上是clr变换所得数据的一组正交变换。因而本文仅介绍clr变换及其度量不变性。

对于满足式(1)的三维单形空间的成分数据x=(x1,x2,x3)，施行clr变换可得到三维向量z=(z1,z2,z3)，其中：

(5)

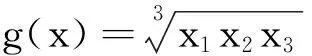
(6)

经过clr变换得到的z=(z1,z2,z3)不再受到定和条件的约束，而且各个分量的取值范围在整个实数范围内，因而z=(z1,z2,z3)是三维欧式空间的常规数据，可以施行常规的统计分析。

clr变换的度量不变性表现为成分数据Aitchison几何可先转化为对变换之后的向量的欧式几何运算，然后借助逆变换表示所得到的新的成分数据。对应于式(2)和式(3)，由clr变换的度量不变性可得：

(7)

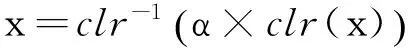
(8)

式(4)的度量不变性则表示：

(9)

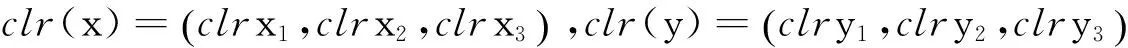
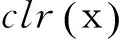
三、整体产业结构同构化指标的构建

(一)结构中心

Aitchison用成分数据的样本均值反映成分数据的集中趋势。根据成分数据的Aitchison几何理论，样本均值在单形空间上反映了产业结构的中心。因此选用成分数据的样本均值来测度产业结构的结构中心，反映同一时期区域产业结构的整体状况。

(10)

(11)

(二)结构离散度

成分数据的方差研究主要有度量方差(metricvariance)和变异方差矩阵(variationmatrix)[17]75-78。变异方差矩阵反映的是成分数据内部各分量比值的离散程度，而度量方差则从几何角度整体分析成分数据与结构中心的离散程度。因而度量方差适用于研究产业结构的整体离散情况。本文以度量标准差(metricstandardvariance)来定义结构离散度，并作为整体反映产业结构同构化的指标。

(12)

对于三维成分数据产业结构D=3，则产业结构结构离散度scatter(x)为：

(13)

由于结构离散度scatter(x)具有无偏性等统计性质[17]75-78，因而是一个好的统计量。结构离散度scatter(x)的取值非负。当scatter(x)越接近0，则表示第t时期的产业结构同构程度越高，当scatter(x)的值越大，表示第t时期的产业结构同构程度越低。

四、产业结构整体同构化的实证分析

(一)相关说明

2003年新的国民经济行业分类GB/T4754-2002开始实施，三次产业结构的统计口径与2003年之前不同，部分省份的产业结构数据未能相应的调整，本文研究的时间区间为2003—2013年。

根据《中国统计年鉴》(2004—2014)，收集2003—2013年中国31个省份的三次产业结构数据以及中国东部、中部、西部以及东北地区四个区域(见表1)的产业结构数据，运用产业结构离散度指标测度中国31个省份间以及四大区域内部的产业结构的同构化程度，从而整体上把握中国31个省份间以及不同区域间的同构化程度的差异。

表1　中国31个省份的区域划分

(二)图形呈现

根据中国31个省份的产业结构数据，可绘制每年的产业结构三元图，直观反映产业结构的分布情况。由于篇幅关系，仅绘制2003年、2007年、2010年以及2013年产业结构的三元图，见图2。图中的空心点表示对应年份的省份产业结构数据，实心点表示对应年份的结构中心。从结构中心来看，2003—2013年间中国31个省份的第一产业比重不断降低，第二产业始终占据主导地位，然而第二产业比重不断下降，第三产业比重不断上升，第二产业的主导地位逐渐变弱。具体产业结构离散程度的变化需要通过测算来反映。

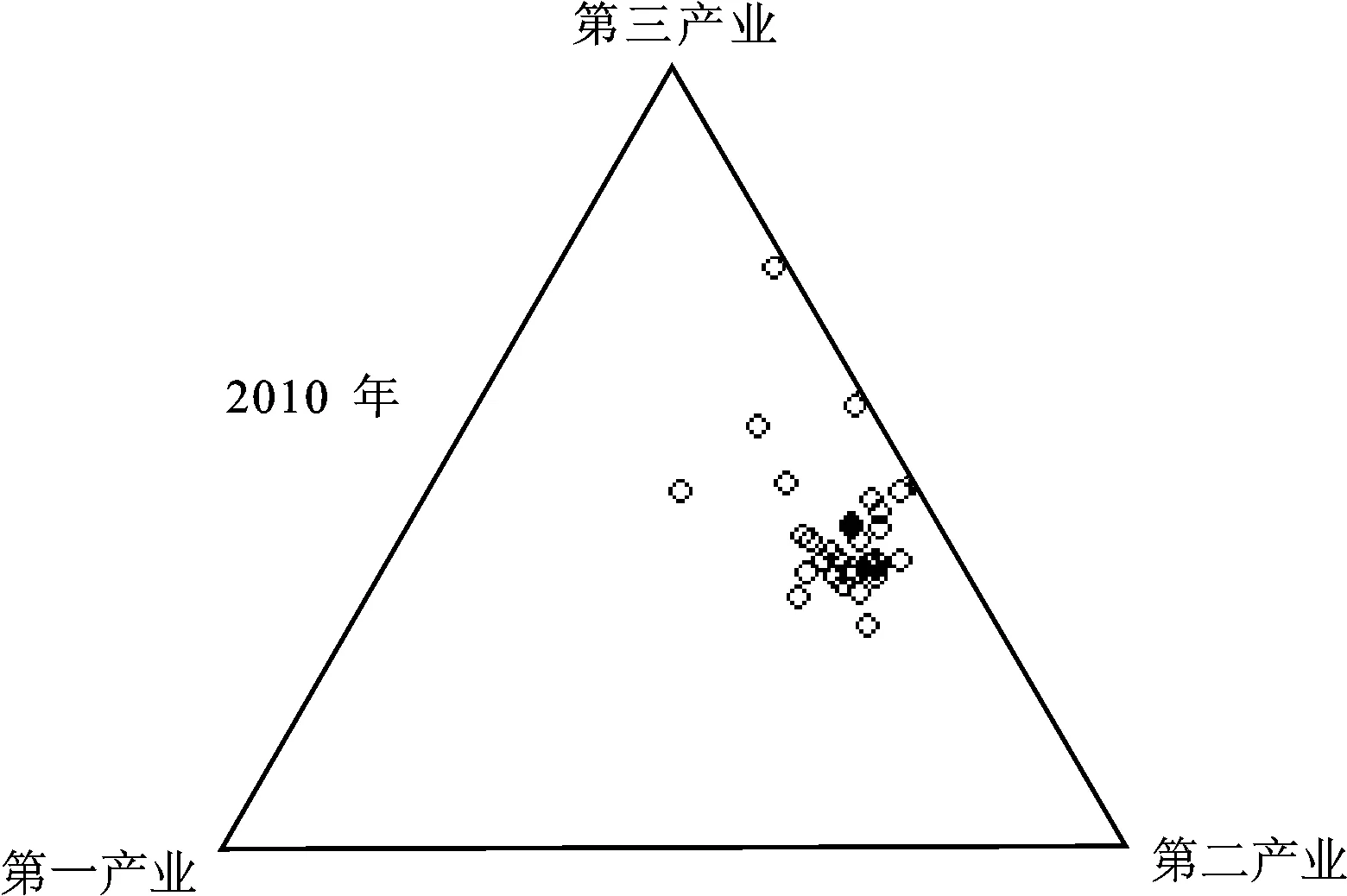
图2　不同年份的中国31个省份产业结构三元图

同样，根据中国不同区域的产业结构数据，可以绘制不同区域每年的产业结构三元图。由于篇幅关系，仅绘制2013年中国不同区域的产业结构的分布以及结构中心，见图3所示。从结构中心来看，2013年东部地区的第一产业比重较低，第二产业比重和第三产业比重比较接近，而其他三个区域虽然第一产业结构比重较低，但是第二产业占主导地位。从结构分布的离散程度来看，2013年东部地区10个省市的分布比较分散，离散程度比较明显，而其他三个区域则相对比较集中。

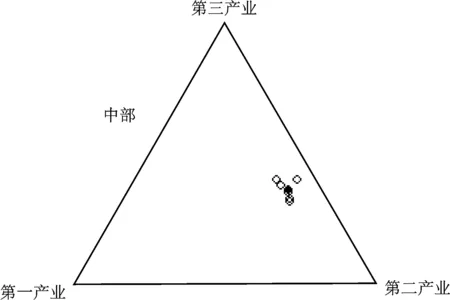
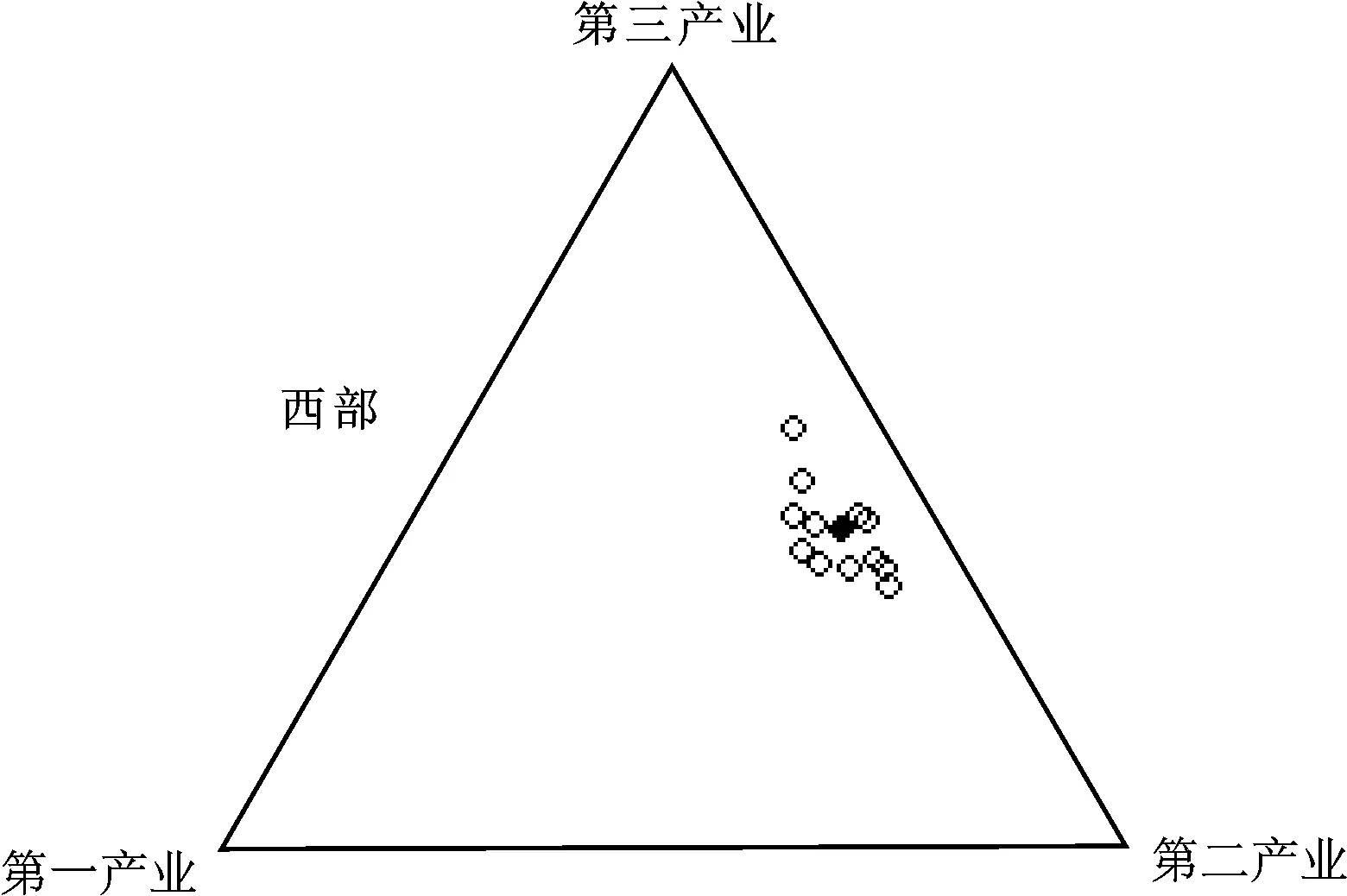
图3　2013年中国不同区域产业结构三元图

(三)产业结构同构化指标测算和分析

根据中国31个省份以及不同区域的产业结构数据，根据结构中心的计算式(6)和(10)以及结构离散度的计算式(13)分别计算结构中心和结构离散度指标，汇总见表2和表3。类似可计算中国不同区域产业结构的结构中心值，由于篇幅关系，具体计算结果略去。绘制中国31个省份整体的结构离散度以及不同区域的结构离散度变化趋势图，见图4。

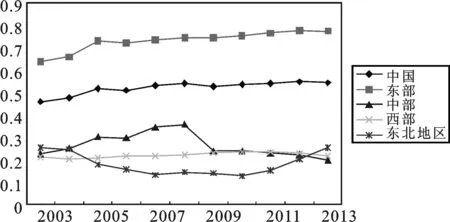
图4　中国及其不同区域产业结构的结构离散度

由表2看出，中国31个省份产业结构的结构中心的演变特点：1.第一产业比重呈下降趋势，从2003年的13.4%下降到2013年的8.7%；2.第二产业始终占据主导地位；第二产业比重小幅波动，变化不大；从2003年的46.5%变化到2013年的48.5%，整体上升了2个百分点；3.第三产业比重也呈现小幅波动，从2003年的40%变化到2013年的42.8%，整体上升了2.8个百分点。

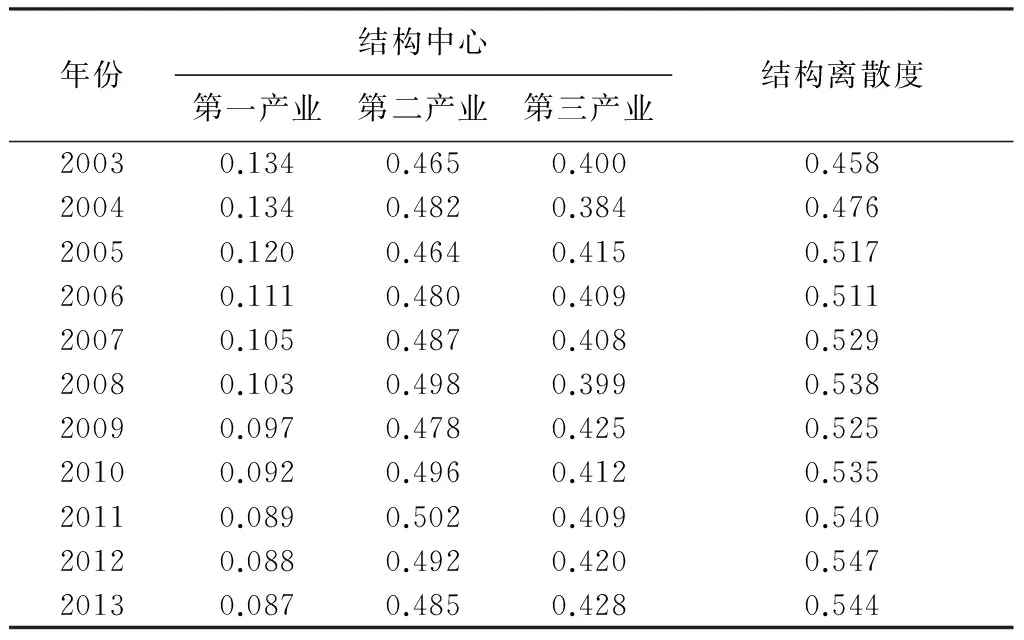
表2　中国31个省份产业结构的结构中心和结构离散度

中国不同区域产业结构的结构中心呈现以下变化：1.东部、中部以及西部区域的第一产业比重持续下降，分别由2003年的8.1%、16%和18.4%下降到2013年的4.5%、11%和11.9%；而东北地区的第一产业比重相对比较稳定，呈现先降后升的趋势，由2003年的13.2%下降到2010年的11%，然后上升到2013年的12.2%； 2.中部、西部和东北地区的第二产业始终占据主导地位，东部地区的第二产业主导地位则逐渐被第三产业所取代， 2009年第三产业比重48.2%首次超过第二产业比重46.6%，第三产业主导地位不断加强，第三产业比重稳步上升，2013年达到50.7%，第二产业比重则持续下降至2013年的44.8%。

由图4的结构离散度可以看到：1.中国31个省份的产业结构离散度从2003年的0.458上升到2005年的0.517，随后下降到2006年的0.511，2007年以来在0.525～0.547之间波动。表明2003—2013年间中国产业结构整体同构化程度呈现下降趋势，趋同状况有所缓和。2.不同区域的产业结构同构化呈现明显的差异性：东部10个省份自2003年以来结构离散度从0.636扩大到2012年的0.775，2013年略微下降到0.772，表明东部产业结构同构化程度较低，呈现趋异性；中部6个省份的产业结构离散度先升后降，从2003年的0.226上升到2008年的0.357，然后下降到2013年的0.2，表明中部产业结构呈现先趋异而后趋同，现阶段产业结构不断趋同；西部12个省份的产业结构离散度比较平稳，自2003年的0.212平稳上升到2011年的0.234，随后下降到2013年的0.218；东北地区的结构离散度呈现先降后升的趋势，从2003年的0.254下降到2010年的0.127，随后上升到2013年的0.255，表明东北地区产业结构呈现先趋同而后趋异的特点。

表3　中国不同区域产业结构的结构离散度

五、结 论

经济结构领域存在着诸如产业结构、消费结构等成分数据类型，已有的研究往往忽略了定和条件约束的成分数据的特性，成分数据统计理论和方法尚未得到广泛应用，一些统计指标有待构建，从而进一步反映经济结构的演进趋势或经济结构间的关系。

已有诸如结构相似系数等指标适用于测度两两地区的产业结构同构化程度，尚缺乏从整体角度来衡量产业结构同构化程度的指标。因而对产业结构的整体同构化指标的研究具有一定的理论价值和应用意义。

本文根据产业结构这一成分数据的特点，基于成分数据统计理论，引入结构中心反映产业结构演变的平均方向，用结构离散度来反映区域产业结构整体同构化程度的度量指标，并对中国31个省份以及不同区域的产业结构整体同构化程度进行研究。研究结果表明：

1.从结构中心即产业结构的平均水平来看，中国31个省份的产业结构仍处于“二三一”阶段，第二产业主导地位保持不变，中部、西部以及东北区域的产业结构处于“二三一”阶段，东部地区自2009年实现“三二一”以来，第三产业的主导地位不断加强。

2.从结构离散度即产业结构的整体同构化程度来看，中国31个省份的同构化程度现阶段比较稳定，东部区域同构化程度最低。不同区域呈现出不同的同构化趋势。现阶段，东部的产业结构的趋异趋势有所降低，中部呈现趋同趋势，东北地区则呈现趋异趋势，西部区域的产业结构同构化没有明显变化。

本文仅对三次产业结构的整体同构化程度进行测度，可以利用结构离散度指标对具体产业结构内部诸如第二产业、第三产业内部以及第二产业内部的制造业等进行区域整体同构化的测度，从整体性上把握区域产业结构的演变趋势，从而为各级政府制定相关产业政策提供参考依据。

[1]冯邦彦,邵帅.珠江三角洲产业结构趋同问题研究[J].工业技术经济,2010(6).

[2]王志华,陈圻. 测度长三角制造业同构的几种方法——基于时间序列数据的分析[J]. 产业经济研究,2006(4).

[3]FingerJM,KreininME.AMeasureof“ExportSimilarity”andItsPossibleUses[J].EconomicJournal,1979,89(356).

[4]何大义,李冉,黄启. 基于信息熵的产业结构同构化程度的度量研究[J].资源与产业,2014 (5).

[5]刘传江,吕力.长江三角洲地区产业结构趋同、制造业空间扩散与区域经济发展[J].管理世界,2005(4).

[6]金戈.长三角地区制造业同构问题再考察——基于雁行模式的视角[J]. 经济地理,2010(2).

[7]刘杰.山东省西部产业结构趋同研究[J]. 经济地理,2013(9).

[8]樊福卓.一种改进的产业结构相似度测度方法[J]. 数量经济技术经济研究,2013(7).

[9]张晓琴,陈佳佳,原静. 成分数据的组合预测[J]. 应用概率统计,2013(7).

[10]王惠文,刘强.成分数据预测模型及其在中国产业结构趋势分析中的应用[J].中外管理导报, 2002(5).

[11]王惠文,黄薇,刘强.北京市三次产业预测分析[J]. 系统理论与实践,2003(6).

[12]施久玉,柴艳有.灰色成分数据模型在中国产业结构分析预测中的应用[J]. 统计与信息论坛, 2007(1).

[13]AitchisonJ.TheStatisticalAnalysisofCompositionalData[M].周蒂,等,译.北京:中国地质大学出版社,1989.

[14]AitchisonJ,EgozcueJJ.CompositionalDataAnalysis:WhereAreWeandWhereShouldWeBeHeading?[J].MathematicalGeology, 2005, 37(7).

[15]EgozcueJJ,Pawlowsky-GlahnV,Mateu-FigeurasG,etal.IsometricLogratioTransformationsforCompositionalDataAnalysis[J].MathematicalGeology, 2003,35(3).

[16]PearsonK.MathematicalContributionstotheTheoryofEvolution.OnaFormofSpuriousCorrelationWhichMayAriseWhenIndicesAreUsedintheMeasurementofOrgans[J].ProceedingsoftheRoyalSocietyofLondon, 1896(1).

[17]GeraldvandenBoogaartKG,Tolosana-DelgadoR.AnalyzingCompositionalDatawithR[M].German:SpringerBerlinHeidelberg,2013.

ResearchontheGlobalIsomorphicTrendofChina'sIndustrialStructure:BasedonCompositionalDataStatistics

HUYu-qin1,2,XUELiu-gen1

(1.CollegeofAppliedSciences,BeijingUniversityofTechnology,Beijing100124,China;2.SchoolofDataSciences,ZhejiangUniversityofFinanceandEconomics,Hangzhou310018,China)

Theexistingisomorphicindexesofindustrialstructureareapplicabletomeasureisomorphismbetweentworegions.Fromthewholeperspective,thispaperproposesanewmethodtomeasuretheisomorphismofindustrialstructureinmanyregions.Basedonthetheoryofcompositionaldatastatistics,thispaperusestheternarydiagramtoreflectthewholeevolutionofindustrialstructureandproposesthestructurecenterandthestructuralscatterdegreetomeasuretheglobalisomorphismofindustrystructure.Usingthoseindexes,thispaperhasanalyzedempiricallytheglobalisomorphismofindustrialstructureof31provincesandcitiesinChinaandtheEastern,Middle,WesternandNortheasternregions.Theresearchnotonlyshowsthattheglobalisomorphismofthe31provincesinChinaisrelativelystableandtheEasternregionisthelowestdegreeinglobalisomorphism.Itbutalsoshowsdifferentregionsshowdifferentisomorphictrend.

industrialstructure;globalisomorphism;compositionaldatastatistics;structurecenter;structurescatterdegree

2016-01-08；修复日期：2016-05-09

国家自然科学基金项目《高维数据的半参数回归建模与统计分析》(11571025)； 国家社会科学基金项目《我国教育回报率的统计分析及与其他国家的比较研究》(13CTJ012)和《相依新息板数据模型的统计推断及应用》(14BTJ031)；浙江省2016年统计科学研究重点课题《产业结构整体同构化测度指标的构建与应用：以浙江省为例》

胡玉琴，女，浙江乐清人，经济学博士，副教授，硕士生导师，研究方向：统计理论方法与应用;

F121.3∶O212

A

1007-3116(2016)08-0032-07

(责任编辑：张治国)

薛留根，男，河南许昌人，教授，博士生导师，研究方向：复杂数据统计。

【统计应用研究】