一类并联负载共享系统可靠性的研究*

郭志图，张正成

（兰州交通大学数理学院，甘肃兰州730070）

一类并联负载共享系统可靠性的研究*

郭志图，张正成

（兰州交通大学数理学院，甘肃兰州730070）

摘要：考虑由两个不同元件构成的并联负载共享系统，该系统至少有一个元件工作才能确保系统正常运行。利用负载分配函数gi（α）与元件在满负载荷环境下虚拟年龄ν（t），w（t）的特性，分析了在条件下，系统可靠度函数。得出了系统可靠度函数为两元件剩余寿命的混合，并结合实例分析了元件寿命服从指数分布时系统在不同特殊情形下剩余寿命的性质。

关键词：可靠性；负载共享；虚拟年龄；指数分布

DOI10.3969/j.issn.1672-6375.2016.03.005

0　引言

可靠性是复杂系统重要的质量指标，电子工程邻域常采用冗余技术提高系统的可靠性能［1］。一般在分析系统可靠性时，均假定系统中已失效元件对其他剩余工作元件的性能没有影响，即元件的失效率不受其工作环境的影响。但实际中，这种假定并不合理，即系统中元件的相继失效可使其他存活元件的失效率改变，继而影响元件的工作寿命。将元件失效率随其工作负载而改变的系统称为负载共享系统。通常情况下，元件负载的增加会导致更高的失效率［2-3］，如牵引吊桥的缆索、固定汽车轮胎的螺丝、计算机CPU系统等均可视为负载共享系统。Shao［4］讨论了一般的n中取k负载系统的可靠性；Lewis［5］给出了负载变化时两元件表决系统可靠性函数；张婧研［6］和谭庆努［7］分别分析了并联可修负载系统和负载系统最大承载模型。为建立元件失效对系统剩余工作元件失效率的影响，Tang［8］构造了new method方法。本论述在此基础上将进一步研究两元件负载共享系统剩余寿命的特性，并求解系统剩余寿命函数。

1　并联负载共享系统概述

并联负载共享系统由两个不同元件组成，系统中至少有一个元件工作才能保证系统正常运作且系统总负载为L。系统开始工作时，元件1和2均在部分载荷下正常工作，并分别以比率a，1-α（0≤α≤1）将总负载为L分配。若系统中某一元件发生故障，另一元件将承载系统总负载，并在满负载荷下继续工作（如图1）。

图1　两元件并联负载共享系统

设变量Xi为元件i（i＝1，2）在满负载荷条件下的寿命，记Xi的分布函数为Fi（t），生存函数为Fi（t）=1-Fi（t）。Xp1，Xp2表示元件i（i＝1，2）在部分载荷pi下的寿命，其分布函数与生存函数分别为Fpi（t）和Fpi（t）=1-Fpi（t）。假定两元件在部分负载工作环境下的工作相互独立，可以看出两元件相互构成储备系统。Won［9］给出了两元件负载系统元件分布函数与负载分配率间关系式，对任意t≥0，

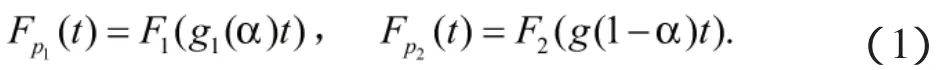
其中，gi（α）（i＝1，2）为负载分配函数。当t≥0时，gi（α）有以下性质：（I）gi（0）＝0，gi（1）＝1；（II）0≤gi（α）≤1；（III）gi（α）关于α是递增函数。设元件i（i＝1，2）在部分载荷条件下（0，u］内未失效，另一元件在t=u时刻恰好失效，u时刻起元件i将在满负载荷下工作。假定元件1（2）在t=u时刻，即满载工作环境下有寿命年龄w1（u）w2（u）。其中，w1（u）为元件i的虚拟年龄，且满足：（I）wi（0）＝0，（II）对u≥0，有wi（u）≤u，（III）wi（u）关于u≥0是递增函数。

2　主要结论

记并联负载系统在min（Xp1，Xp2）＝t条件下的可靠度函数为，元件i（i＝1，2）在部分负载条件下的寿命分别为Xp1，Xp2。若t=u时刻，元件1（2）的虚拟年龄分别为ν（t），w（t），记为第i个元件在满负载荷条件下的剩余寿命。假定元件在部分负载环境下的工作相互独立，则以下定理成立。

定理对任给x≥0，当t≥0时，两元件并联负载系统的剩余寿命可靠度函数为

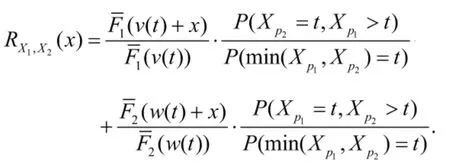
证明：

例考虑由两元件组成的并联负载系统，设元件X1和X2为独立同分布于参数为λ和β的指数分布，其生存函数分别为，。由指数分布的无记忆性，得

又有元件i在满负载条件下条件生存函数分别为

可得

将（3-5）式代入（2）式中得

由（6）式知该可靠度函数是两个服从指数随机变量的混合。特别的，给出以下三种特殊情形：

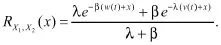
（2）若a=0，即g1（0）＝0，g2（1）＝1时，恰为元件1在满负载荷条件的生存函数。

（3）若a=1，即g1（1）＝1，g2（0）＝0时，恰为元件2在满负载荷条件的生存函数。

3　结束语

本论述考虑了由两不同元件构成的并联负载共享系统，得出了在min（Xp1，Xp2）＝t条件下系统可靠度函数。结合算例，讨论了元件寿命服从指数分布时系统可靠度函数的特殊情形。该结果对研究负载共享系统剩余寿命的性质具有指导意义。论述中只分析了两元件构成的负载共享系统，在三个元件的情形下如何研究系统的剩余寿命将是进一步研究的内容。

参考文献：

［1］K.B.Mishra．Reliability Analysis and Prediction：A Methodology Oriented Treatment［J］．Structural Safety，1992，11（3-4）：263-265．

［2］E.M.Scheuer．Reliability of an m-out-of-n system when component failure induces higher failure rates in survivors ［J］．Microelectronics and Reliability，1989，29（6）：1097．

［3］B.Singh，K.K.Sharma，A.Kumar．Inferences on the dynamic system model with discrete failure time distribution［J］．Statistical Methods and Applications，2009，18（4）：521-542．

［4］Shao Jiajun，Lambersonal．Modeling a shared-load k-out of-n：G system［J］．IEEE Trans on reliability，1991，40（2）：205-208．

［5］E.E.Lewis．A load-capacity interference model for commonmode failures in 1-out of-2：G systems［J］．IEEE Trans on reliability，2001，50（1）：47-51．

［6］张婧，唐应辉.负载分担下可修并联系统的可靠性分析［J］．电子科技大学学报，2007，36（2）：401-403．

［7］谭庆努，魏学业，吴小进，等.负载均担并联系统模型及其可靠性分析［J］．电子科技大学学报，2013，42（2）：311-315．

［8］Tang Ying hui，Zhang Jing．New model for load-sharing k-out of-n：G system with different components［J］．Journal of Systems Engineering and Electronics，2008，19（4）：748-751．

［9］Won Young Yun，Ji Hwan Cha．A stochastic model for a general load-sharing system under overload condition［J］．Applied Stochastic Models in Business and Industry，2009，26 （5）：624-638．

中图分类号：O213.2

文献标识码：A

收稿日期：2015-12-12 项目基金：国家自然科学基金资助项目（编号：71361020）。

作者简介：郭志图（1989-），男，汉族，甘肃白银人，硕士研究生，主要研究方向：系统可靠性。