基于切比雪夫混沌映射的医学信息管理系统安全认证方案*
冉雪江, 薛 康, 曹 莉
(内蒙古医科大学 计算机信息学院,内蒙古自治区 呼和浩特 010110)
基于切比雪夫混沌映射的医学信息管理系统安全认证方案*
冉雪江,薛康*,曹莉
(内蒙古医科大学 计算机信息学院,内蒙古自治区 呼和浩特 010110)
提出一种基于切比雪夫混沌映射的医学信息管理系统安全认证方案.利用基于扩展混沌映射的Diffie-Hellman密钥交换机制来维持医疗用户间会话密钥的安全,无需服务器公钥,且避免了椭圆曲线当量乘法和模幂运算,大大减少了认证计算量.在随机预言模型下给出了该方案的安全性证明.实验结果表明,相比现有的安全认证方案,提出的方案在保持较低复杂度的同时提供了较高的安全性能.
安全认证;医学信息管理;切比雪夫混沌映射;Diffie -Hellman密钥交换;随机预言模型
目前,在病人转诊的过程中,不同级别的医疗机构之间并没有共享患者的疾病治疗过程.所以,建立一个医学信息共享平台能够为医生的诊疗工作提供更详尽的参考作用[1].同时由于个人电子病历信息涉及到诸多个人隐私,如何保护这些信息不被窃取也成为一个非常迫切的研究课题.为此,在医学信息管理系统中需要一种有效的三方安全认证系统,来保证病人、医疗人员和医疗服务器之间的通信安全[2~4].目前,学者提出了一些用于电子医学系统的三方认证方案[5~10].例如,[5]提出了一种高效的三方身份认证方案,该方案不需要服务密钥且可以防止密码文件攻击.然而,该方案不能抵抗校验值丢失攻击.[10]提出一种基于混沌理论的身份识别方案.但是,这些电子医学系统安全认证方案都存在一些安全性弱点.
本文提出一种基于切比雪夫混沌映射的医学信息管理系统三方安全认证方案,利用基于扩展混沌映射的Diffie-Hellman密钥交换机制来维持用户间会话密钥的安全,不需要服务器公钥,且避免了大量计算.
1 提出的安全认证方案
本文方案由两部分密钥交换方案组成,一部分为A和S之间的密钥交换,另一部分为B和S之间的密钥交换,然后结合了一个基于扩展混沌映射的Diffie-Hellman密钥交换协议实现A和B之间的密钥交换.
1.1三方身份认证
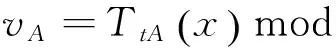
步骤1:A→S:A,B,XA.
A计算出XA=Ta(x)modp,并将(A,B,XA)发送给S,其中a为一个随机数.
步骤2:S→B:XA,XSA,XSB.
收到A发送的请求信息后,S检索出vA和vB,并计算XSA=(Tc(x)modp)⊕vA和XSB=(Td(x)modp)⊕vB,其中c,d为随机数.然后S将(XA,XSA,XSB)发送到B.
步骤3:B→A:XB,XSA,μBS,μBA.
收到S发送的信息后,B计算XB≡Tb(x)modp,Td(x)≡XSB⊕vB,KBS≡(Tb(Td(x))⊕TtB(Td(x)))modp,μBS=h(B,S,XB,XA,KBS),KBA≡Tb(XA)≡Tb·a(x)modp,μBA=h(B,A,XB,XA,KBA),其中b为一个随机数,tB=h(B,S,πB),然后将(XB,XA,μBS,μBA)发送到A.
步骤4:A→S:μAS,μBS,XB,μAB.
收到B发送的信息后,A计算Tc(x)=XSA⊕vA,KAS≡(Ta(Tc(x))⊕TtA(Tc(x)))modp,μAS=h(A,S,XA,XB,KAS)和KAB≡Ta(XB)≡Ta·b(x)modp,其中tA=h(A,S,πA).如果A成功满足μBA,则A计算μAB=h(A,B,XA,XB,KAB),并将计算结果(μAS,μBS,XB,μBA)发送给S.
步骤5:S→B:μSA,μSB,μAB.
S计算KSA≡(Tc(vA)⊕Tc(XA))modp和KSB≡(Td(vB)⊕Td(XB))modp.如果S成功认证μAS和μBS,则计算μSB=h(S,A,XA,XB,KSA)和μSB=h(S,B,XB,XA,KSB),并发送(μSA,μSB,μAB)给A.
步骤6:B→A:μSA.
经过上述过程之后,如果B成功满足μAB和μSB,然后B将μSA发送给A,A认证μSA,然后A和B协商一个共同会话密钥SK=h(A,B,S,XA,XB,KAB)=h(A,B,S,XA,XB,KBA).
1.2循环三方身份认证
本文提出的高效循环身份认证方案重新排序了三方身份认证方案的计算步骤,分为四个步骤.
步骤1:(1)A→S:A,B;(2)A→B:A,XA.
A发送请求信息(A,B)给S.同时,A计算XA≡Ta(x)modp,并将结果(A,XA)发送给B.
步骤2:(1)S→A:XAB;(2)S→B:XSB;(3)B→S:A,B,XB;B→A:B,XB.
S检索出vA和vB,并计算XSA=(Tc(x)modp)⊕vA和XSB=(Td(x)modp)⊕vB.然后S发送XSA到A,并发送XSB到B.同时,B计算XB≡Tb(x)modp,并将结果(A,B,XB)发送给S,将(B,XB)发送给A.
步骤3.(1)A→S:μAS;(2)A→B:μAB;(3)B→S:μBS;(4)B→A:μBA.
A计算Tc(x)=XSA⊕vA,KAS≡(Ta(Tc(x))⊕TtA(Tc(x)))modp,μAS=h(A,S,XA,XB,KAS)和KAB≡Ta(XB)modp.然后A认证μBA,计算μAB=h(A,B,XA,XB,KAB),并将(μBS)发送给S,同时将(μAB)发送给B.此时,B计算Td(x)=XSB⊕vB,KBS≡(Tb(Td(x))⊕TtB(Td(x)))modp,μBS=h(B,S,XB,XA,KBS),KBA≡Tb(XA)modp,和μBA=h(B,A,XB,XA,KBA).然后B将(μBS)发送给S,同时将(μBA)发送给A.
步骤4:(1)S→A:μSA;(2)S→B:μSB.
S计算KSA≡(Tc(vA)⊕Tc(XA))modp和KSB≡(Td(vB)⊕Td(XB))modp,并认证μAS和μBS.然后S计算μSA=h(S,A,XA,XB,KSA)和μSB=h(S,B,XB,XA,KSB),并将(μSA)发送给A,将(μSB)发送给B.最后,A认证μBA和μSA.B认证μAB和μSB.此外,A和B协商共同会话密钥SK=h(A,B,S,XA,XB,KAB)=h(A,B,S,XA,XB,KBA).
2 安全性能分析
引理1定义A,B和F为具有一定概率分布的事件,假设A∧┐F⟺B∧┐F,然后就有
|Pr[A]-Pr[B]|≤Pr[F].
为了获得密钥交换(AKE)安全方案,本文利用包含A和S的2PAKE方案来建立此方案.下面的定理显示:如果结合Hash函数能够增强安全性,且基于扩展混沌映射的决策性Diffie-Hellman(DDH)假设是成立的,则包含A和S的双方认证密钥交换(2PAKE)方案具有AKE安全性.
定理1令Advadh为一个DDH攻击者,其在t1时间内能够解决扩展混沌映射问题.则攻克包含A和S的2PAKE方案中AKE安全性的概率表示为:
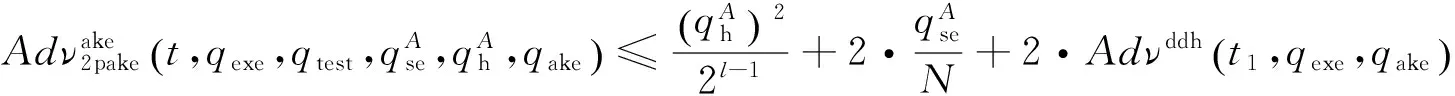

证明每个博弈Gi定义攻击者赢得本轮博弈(事件Ei)的概率.第一次博弈G0是对2PAKE方案的真正攻击,最后博弈G4总结出攻击者攻克2PAKE方案中AKE的安全性的概率很低.
博弈G0:这场博弈会对实际攻击做出回应.根据定义,有

(1)


(2)
博弈G2:本轮博弈除了用表H模拟了包含A和S的Hash查询外,还模拟了上面提及到的所有预言机.结果显示,除了G3中的H表不吻合模拟结果外,G1和G2都吻合.因此,根据生日悖论定理和引理1,有下式:
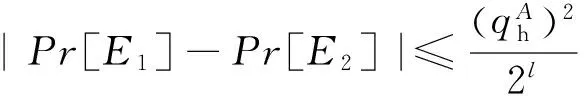
(3)
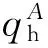

Pr[E2]=Pr[E3].
(4)
博弈G4:本轮博弈模拟了上面博弈中提及到的所有预言机,但不包括利用取自随机分布(Tu(x),Tv(x),Tw(x),)中的三维(x,y,z)所计算的所有规则.取而代之的是扩展的混沌映射DDH图.
假设Addh是一个试图违反扩展混沌映射DDH不可分辨性问题的挑战者;Aake是一个试图攻克会话密钥安全的攻击者.Addh在α∈{0,1}内随机取值,并且为Aake返回真正的会话密钥KAS(如果α=1)或一个随机字符串(如果α=0).然后Aake输出它的猜想α′,如果α′=α,则猜想正确.接着Addh提问一个Send、Corrupt或Test查询.Addh执行前面的实验后返回输出值,如果Addh输出α,则Addh输出1;否则,输出0.如果(x,y,z)符合扩展混沌映射图,则Addh在G3中执行Aake,因此Pr[Addh输出1]=Pr[E3].如果(x,y,z)为三维随机数,则Addh在G4中执行Aake,因此Pr[Addh输出1]=Pr[E4].所以,可得:
|Pr[E3]-Pr[E4]|≤Advddh(A)ddh.
(5)
因为所有会话密钥是随机的、独立的,同时也未曾泄露关于α的信息,所以可以得出:
Pr[E4]=1/2.
(6)
3 性能比较
表1列出了本文方案与其他用于电子医学系统的三方身份认证方案性能比较的结果.表中TE表示执行一个模幂运算的时间;TM表示执行一个模乘运算的时间;TC表示执行一个切比雪夫多项式计算的时间;TH表示执行一个Hash运算的时间;TR表示生成一个随机数的时间.其中,TC的值要远小于TE.
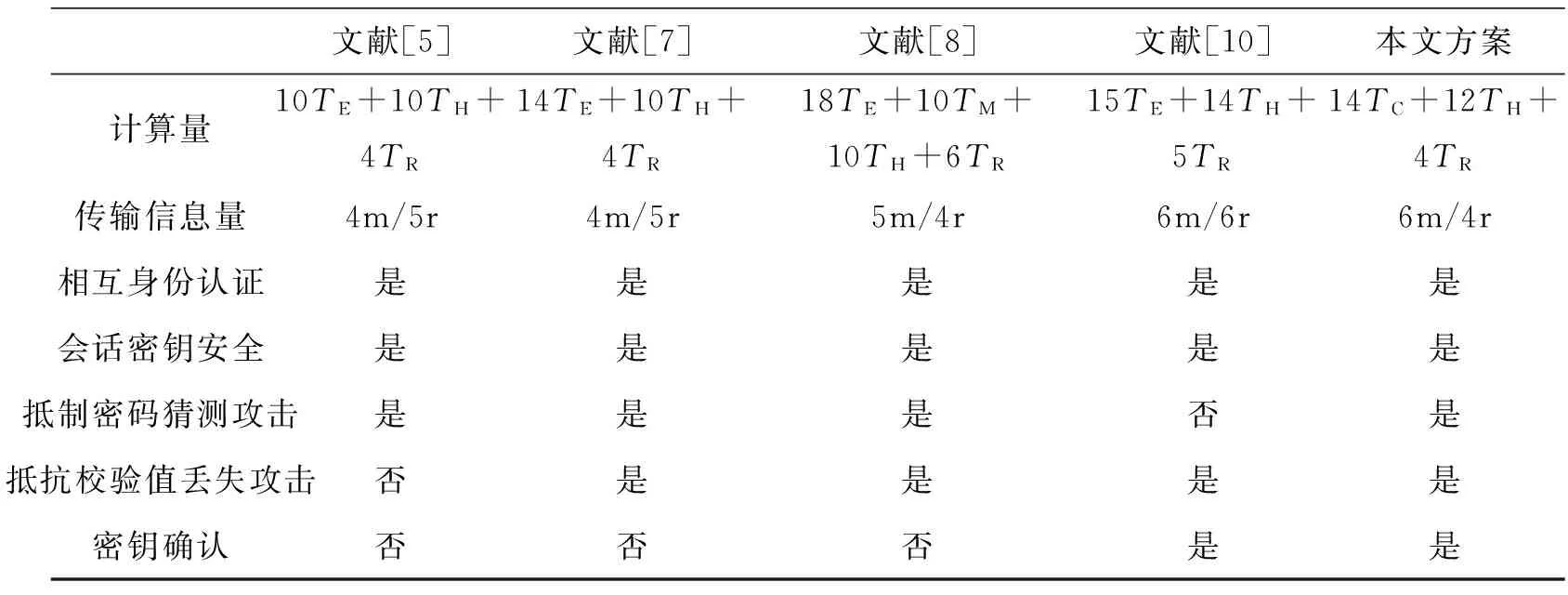
表1 相关身份认证方案的性能比较Tab.1 The performance comparison of identity authentication scheme
从表1可以看出,在计算量方面,其他方案都需要执行多个耗时的模幂运算.然而,本文方案充分利用了拓展混沌映射,用切比雪夫多项式计算替代了模幂运算,计算效率大大提高.在传输信息量方面,[10]需要6条信息进行6次循环,本文方案需要6条信息进行4次循环,但比其他几个方案的传输信息量要略大.在本文方案中,两个参与者之间(A-S或B-S)不需要公共密钥进行身份认证和互相回应,要实现三方身份认证,则至少需要参与者的6条认证信息.此外,发起者(A)是启动信息的唯一人,另外两人(B和S)在接收到发起者的信息瞬间进行认证.然后B和S在第一回合中进行相互身份认证,并回应发起者A的信息认证.因此,执行不需要公共密钥的三方身份认证方案至少需要经过4次循坏.
在安全性能方面,本文方案能够提供相互身份认证、会话密钥的安全性和密码确认的安全性,同时能够抵抗密码猜测和校验值丢失攻击,比其他方案的安全性都高.因此,本文方案在没有大幅提高信息传输量的同时,获得了较低计算量和较高的安全性能.
4 结束语
本文基于切比雪夫混沌映射机制提出了一种高效安全的医学信息管理系统远程三方身份认证方案.利用基于扩展混沌映射的Diffie-Hellman密钥交换机制来维持用户间会话密钥的安全,使参与者的认证信息量和计算量较少.在随机预言模型下证明了本文方案的安全性,非常适合应用于电子医学信息管理系统中来保证数据交换的安全性.
[1]姚力, 李哲. 医院电子病历安全保障体系构建[J]. 中国医疗设备, 2015, 30(6):92-94.
[2]施荣华, 王伟, 董健. 基于身份密码体制的电子病历系统安全方案[J]. 计算机应用研究, 2013, 30(7):2 140-2 143.
[3]KIAH M L M, NABI M S, ZAIDAN B B, et al. An enhanced security solution for electronic medical records based on AES hybrid technique with SOAP/XML and SHA-1[J]. Journal of Medical Systems, 2013, 37(5):1-18.
[4]LEE Y J. An authentication model based fingerprint recognition for electronic medical records system[J]. Kips Transactions Partc, 2011, 18(6):379-388.
[5]LIN T H, LEE T F. Secure verifier-based three-party authentication schemes without server public keys for data exchange in telecare medicine information systems[J]. Journal of Medical Systems, 2014, 38(5):1-9.
[6]LIU T, PU Q, ZHAO Y, et al. ECC-based password-authenticated key exchange in the three-party setting[J]. Arabian Journal for Science & Engineering, 2013, 38(8):2 069-2 077.
[7]CHIEN H Y. Secure verifier-based three-party key exchange in the random oracle model[J]. Journal of Information Science & Engineering, 2011, 27(4):1 487-1 501.
[8]LIN T H, LEE T F. Secure verifier-based three-party authentication schemes without server public keys for data exchange in telecare medicine information systems[J]. Journal of Medical Systems, 2014, 38(5):1-9.
[9]赵耿, 孙锦慧. 一种基于混沌映射的可否认认证方案[J]. 北京电子科技学院学报, 2013, 21(4):1-4.
[10]HAO X, WANG J, YANG Q, et al. A chaotic map-based authentication scheme for telecare medicine information systems[J]. Journal of Medical Systems, 2013, 37(2):212-217.
责任编辑:龙顺潮
Security Authentication Scheme Base on Chebyshev Chaotic Maps Mechanism in Medical Information Management System
RANXue-jiang,XUEKang*,CAOLi
(School of Computer Information, Inner Mongolia Medical University, Hohehot 010110 China)
A remote security authentication scheme based on Chebyshev chaotic maps mechanism in medical information security management system is proposed. The Diffie-Hellman key exchange mechanism based on extended chaotic map is used to maintain the security of session key, to make it do not require the server public key. And it avoids the elliptic curve equivalent multiplication and modular exponentiation, which will help greatly reduce the calculation. In addition, the security of the scheme is proved in the random oracle model. The proposed scheme has higher security performance while keeping the low complexity comparing with the existing schemes.
security authentication;medical information management; Chebyshev chaotic maps; Diffie-Hellman key exchange; random oracle model
2015-07-06
内蒙古医科大学校级教改课题(NYJGB12014B)
薛康(1979-),男,内蒙古 呼和浩特人,副教授. E-mail:469654001@qq.com
TP309
A
1000-5900(2016)01-0106-05

