基于逐步优化构造新息背景值和倒数累加生成的非等间距多变量新息MGRM(1,n)模型*
韩朝晖 , 韩 乐
(1.湖南文理学院,湖南 常德 415000;2.中南大学 建筑与艺术学院,湖南 长沙 410000)
基于逐步优化构造新息背景值和倒数累加生成的非等间距多变量新息MGRM(1,n)模型*
韩朝晖1*,韩乐2
(1.湖南文理学院,湖南 常德 415000;2.中南大学 建筑与艺术学院,湖南 长沙 410000)
应用逐步优化和新息建模方法,构造多变量非等间距新息灰色模型MGRM(1,n)的新息背景值,基于倒数累加生成,以数据的第m个分量作为灰色微分方程解的初始条件,建立了多变量非等间距新息模型MGRM(1,n).该新型模型不仅适合于等间距建模,也适合于非等间距建模,拓广了灰色模型的应用范围,有效地提高了模型的拟合精度和预测精度.实例证明了所建模型的实用性与可靠性.
倒数累加生成;非等间距序列;逐步优化建模;新息;MGRM(1,n)模型;最小二乘法
灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论.灰色预测模型是灰色系统理论的一个重要内容,灰色预测用数据处理的方法寻找数据间的规律,因而它弥补了现有数据挖掘方法的不足,为数据挖掘提供了新的科学方法.灰色预测模型种类较多,但主要是GM(1,1)、GM(1,N)和MGM(1,N)等[1~3].本文吸收[4]的新息建模和逐步优化思想和方法,构造多变量非等间距灰色新息模型MGRM(1,n)的新息背景值计算公式,基于倒数累加生成建模原理建立了多变量非等间距灰色新息模型MGRM(1,n).该模型不仅适合于等间距序列数据建立模型,也适合于非等间距序列数据建立模型,拓广了灰色模型的应用范围,该新模型精度高,具有很好的理论价值和工程应用前景.
1 基于逐步优化构造新息背景值和倒数累加生成的非等间距多变量新息模型MGRM(1,n)
设多变量的原始数据矩阵为


为了建立灰色模型,先对原始数据进行一次累加生成处理,得到新的矩阵
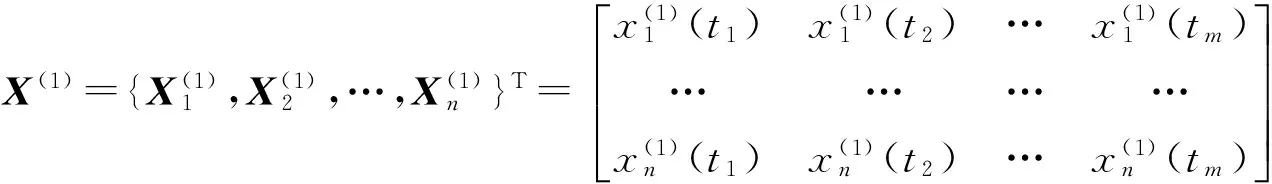
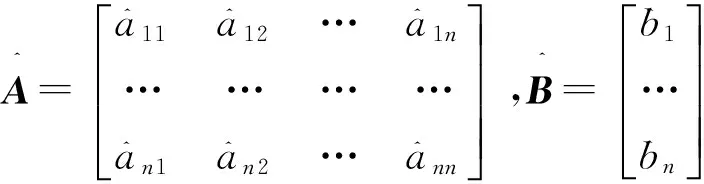
倒数累加生成多变量非等间灰色模型MGRM(1,n)为n元一阶微分方程组

(2)
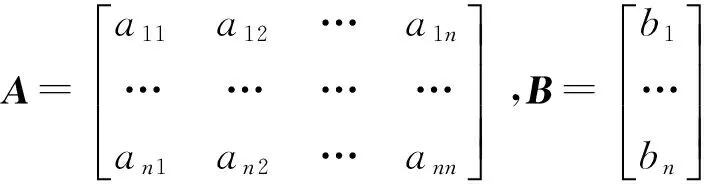
X(1)(t)=eAtX(1)(tm)+A-1(eAt-I)B,
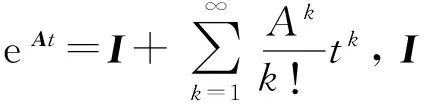



以差分商近似代替微是白化灰导数的方法中最直观、最容易理解方法,即


(1) 对于数据(1),取迭代步数初值j=0,取初值aj=0,此时有


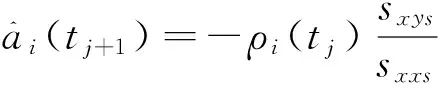

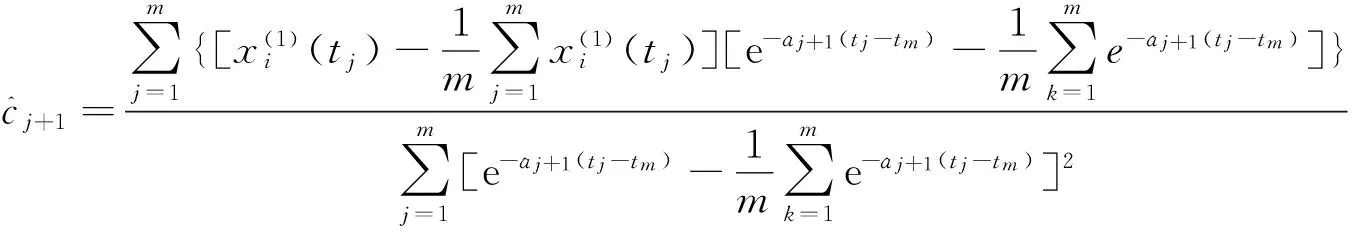


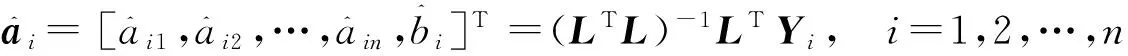

基于倒数累加生成的新息MGRM(1,n)模型的计算值为
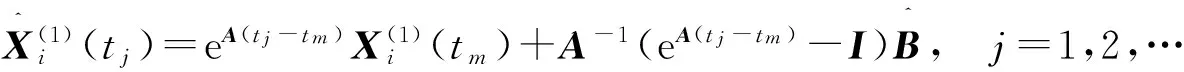
还原得原始数据的拟合值为:
2 模型应用实例
例1在载荷600 N时,TiN薄膜涂层试验数据如表1所示.

表1 TiN薄膜涂层试验数据[8]Tab.1 TiN thin-film coating test data

例2在接触强度计算中,当主曲率函数F(ρ)已知时,一般采用查表方法得到点接触椭圆的长短半径a、b的系数ma、mb.但查表较为繁琐,容易出错,为此用本文的模型进行研究,其数据摘录于表2[9].

表2 TiN薄膜涂层试验数据[9]Tab.2 The values of F(ρ), ma and mb

主曲率函数F(ρ)拟合值为
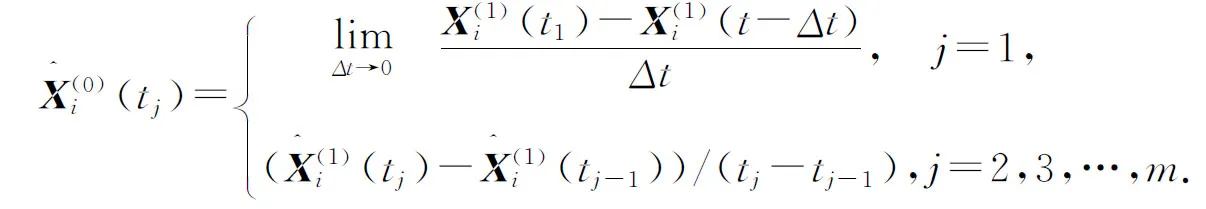
主曲率函数的绝对误差为:
q=[-0.001 432 7,-0.000 996 82,-0.000 689,-0.000 983 28,-0.001 29,-0.001 582 8,-0.001 833 2, -0.002 095 3,-0.002 32 5,-0.002 481 3,-0.002 626 3,-0.002 740 9,-0.002 811,-0.002 819 6, -0.002 754 3,-0.002 849 4,-0.002 988 8,-0.002 907 1,-0.002 855 4,-0.002 973 8,-0.002 982 9, -0.003 023 2,0.003 091 8,-0.003 032 5].
主曲率函数的相对误差(%):
e=[-0.143 34,-0.099 781,-0.069 038,-0.098 624,-0.129 51,-0.159 07,-0.184 43,-0.211,-0.234 37,-0.250 39,-0.265 29,-0.277 14,-0.284 52,-0.285 67,-0.279 34,-0.289 28,-0.303 74,-0.295 74,-0.290 78,-0.303 14,-0.304 38,-0.308 8,-0.316 14,-0.310 39].
相对误差平均值为0.237 25%.模型精度很高.
3 结 论
应用逐步优化和新息建模方法推导了多变量非等间距新息灰色模型MGRM(1,n)新息背景值的计算式, 并以数据的第m个分量作为灰色微分方程解的初始条件,建立了倒数累加生成多变量非等间距灰色新息模型MGRM(1,n).该新模型不仅适合于等间距数据序列建立模型,也适合于非等间距数据序列建立模型,将等间距灰色建模拓展到非等间距建模,拓广了灰色模型的应用范围.新模型具有精度高、使用简便等特点,具有重要的现实意义和理论意义.计算实例表明所建立的模型正确与可靠,值得在工程实践中推广应用.
[1]罗佑新,张龙庭.灰色系统理论及其在机械工程中的应用[M].长沙:国防科技大学出版社,2001.
[2]LUO Y X, WU X, LI M,et al.Grey dynamic model GM(1,N) for the relationship of cost and variability[J]. Kybernetes,2009,38(3): 435-440.
[3]LUO Y X,LI J Y. Application of multi-variable optimizing grey model mGM(1,n,q,r) to the load-strain Relation[C]//The 2009 IEEE International Conference on Mechatronics and Automation (ICMA 2009).Changchun, China,2009:4 023-4 027.
[4]XIONG P P,DANG Y G,YANG Y. The optimization of background value in multi-variable non-equidistant model [C]//19th Chinese Conference on Grey Systems, 2010: 277-281.
[5]崔立志, 刘思峰, 吴正朋. 基于向量连分式理论的MGM(1,m)模型[J]. 系统工程, 2008, 26(10): 47-51.
[6]CUI L Z, LIU S F, WU Z P. MGM(1,m) based on vector continued fractions theory[J]. Systems Engineering, 2008,26(10): 47-51.
[7]罗佑新. 非等间距新息GM(1,1)的逐步优化模型及其应用[J].系统工程理论与实践,2010,30(12) : 2 254-2 257.
[8]LUO Y X. Non-equidistant step by step optimum new information GM(1,1) and its application [J]. Systems Engineering-Theory & Practice,2010,30(12): 2 254-2 257.
[9]杨保华,张忠泉.倒数累加生成灰色GRM(1,1)模型及应用[J].数学的实践与认识2003,33(10):21-25.
责任编辑:龙顺潮
The Non-equidistant New Information MGRM(1,n) Based on a Step by Step Optimum Constructing New Information Background Value and Accumulated Generating Operation of Reciprocal Number
HANZhao-hui1*,HANLe2
(1.Hunan University of Arts & Science,Changde 415000;2.College of Arts and Architecture,Central South University,Changsha 410000 China)
Applying a step by step optimum and new information modeling method to construct new information background value of multi-variable non-equidistance new information Grey model MGRM(1,n), based on accumulated generating operation of reciprocal number, taking themcomponent of each variable as initial value of response function,the multi-variable non-equidistance new information Grey model MGRM(1,n) was built. The proposed model can be used to build model in non-equal interval & equal interval time series, enlarges the scope of application, and advances the model’s fitting precision and prediction precision. Example validates the practicability and reliability of the proposed model.
accumulated generating operation of reciprocal number; non-equidistance sequence; a step by step optimum modeling; new information; non-equidistance MGRM(1,n); least square method
2015-08-12
国家自然科学基金项目(51178465);中南大学博士生自主探索创新项目(2015zzts004);中南大学研究生科研创新项目(2013zzts129);湖南省教育厅教学改革研究重点项目(湘教通[2012]401号359项)
韩朝晖(1962-),男,湖南 常德人,教授. E-mail:2838277807@qq.com
O231
A
1000-5900(2016)01-0010-05

