压缩感知的改进小波抗噪识别系统设计*
茅正冲, 邵朱宇
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
压缩感知的改进小波抗噪识别系统设计*
茅正冲, 邵朱宇
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
根据小波树稀疏性的好坏自适应分配观测数目,然后由观测数目调整小波树的节点个数,使小波树中节点数目与观测数目不匹配的问题得以解决。将预处理后的语音信号经改进小波去噪,进而通过Gammatone滤波器组,提取特征参数GFCC。在高斯混合模型下仿真实验进行。结果表明:该方法与传统非稀疏性适应观测的小波去噪方法相比信噪比提高了14 %,有效削弱了语音信号中噪声的影响,且系统的识别率与鲁棒性都有明显提高。
压缩感知; 小波去噪; 稀疏性适应观测; 抗噪算法; 识别率
0 引 言
压缩感知作为近些年新兴的信号处理技术,是一种在采样过程中利用较少数据就能有效提取信号信息,然后通过重构算法从采样信息中恢复原信号的方法[1]。信号的稀疏性是压缩感知的前提和基础,但是正如语音和图像等信号,它们本身并不是稀疏的,但可以通过某种变换在其变换域中得到一个稀疏的信号以此来适用压缩感知。对于语音信号通常可以转换到离散余弦变换(DCT)域、小波域等变换域来获得稀疏信号。
本文提出的基于压缩感知的改进小波抗噪识别系统,根据语音帧稀疏性的好坏为语音帧分配不同的观测数,再根据观测数目调整小波树节点的个数,最后由观测值重构小波树模型,得到经小波处理后的语音信号。实验结果证明,与传统小波抗噪方法相比,平均信噪比提高了14 %。
1 小波树稀疏性适应观测压缩感知
1.1压缩感知基本原理
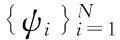
1.2语音信号小波树模型
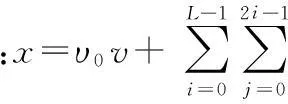
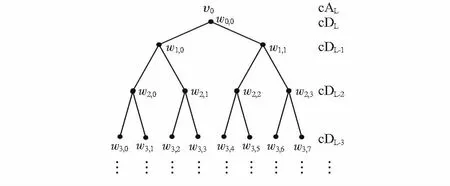
图1 小波树模型Fig 1 Wavelet tree model
虽然系数向量Θ具有一定的稀疏性,但是直接观测并不能得到最好的重构效果。为此利用压缩排序选择算法CSSA[4]对小波树进行修剪来获得更好的稀疏性,且与原信号保持较小的误差。定义k稀疏的小波树模型信号为
(1)
Ω中的非零系数形成相连的子树,以此逼近原始信号
S*=argmax{B(S)}
(2)
式中S为系数向量Θ的索引,代表节点位置,S*为小波树中最大能量的节点,B(S)为系数向量Θ的能量序列。尺度系数υ为初始默认选中的节点,若S*的父节点p(S*)在子树中未被选中,则节点S*及其父节点p(S*)进行压缩合并成一个超节点,并更新它们的取值为其平均值;若父节点p(S*)已被选中,则S*也标记为选中。然后更新迭代次数
t=t+n(S*)
(3)
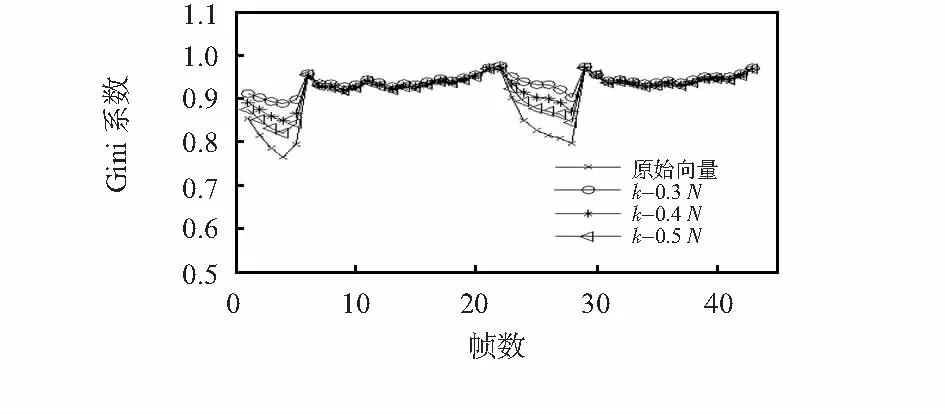
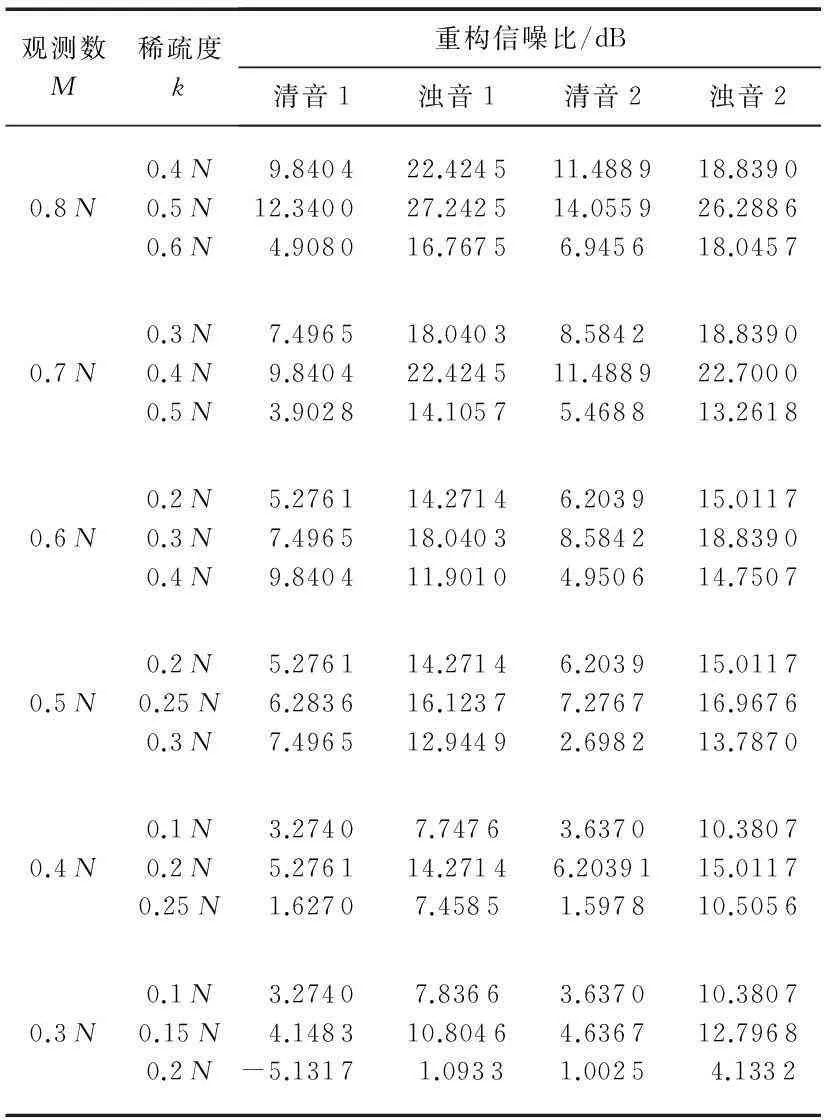
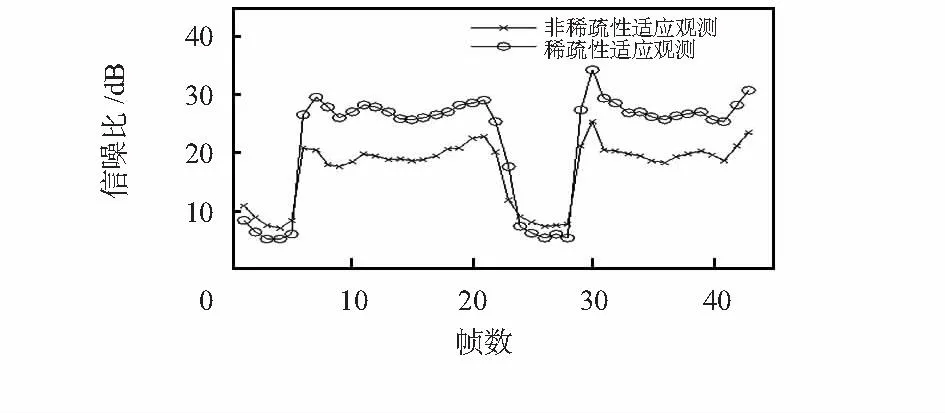
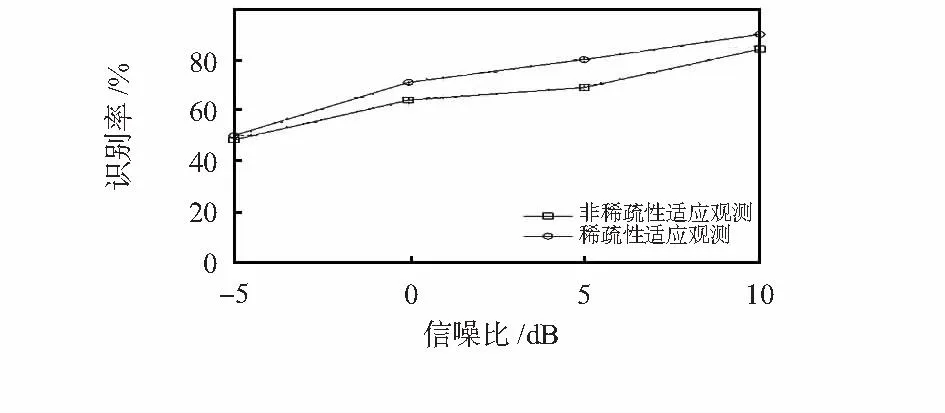
式中n(S*)为当前节点S*包含的节点个数,t为当前迭代次数。当t 1.3小波树稀疏性适应观测 带噪语音信号可以粗略分为噪声段、带噪清音段和带噪浊音段。其中带噪浊音段包含了绝大部分的语音信息,有着比较规律的谐波性,在变换域中呈现出良好的稀疏性,由于噪声信号一般稀疏性较差,所以在重构时能滤除该段部分噪声[6];而其他声音段语音信息量小,稀疏性差,重构效果不理想。压缩感知原理指出,观测数目越多对于信号的重构效果越好。为此,对稀疏性好信息量大的语音帧分配较多的观测数目;对稀疏性差信息量小的语音帧则分配较少的观测数目,虽然这会导致重构不精确,但由于该部分语音帧信息量较小,较低的重构信噪比并不会影响语音整体的重构效果。在小波树模型中,对系数向量Θ进行稀疏性的判断,这里用Gini系数[7]来表征信号的稀疏性 (4) Gammatone滤波器能很好地模拟人耳基底膜的分频特性,本文通过该滤波器组提取特征参数GFCC。先对带噪信号作预处理(预加重、分帧和加窗)和基于本文算法的压缩重构,然后将恢复的信号通过一组64通道的Gammatone滤波器组,其中心频率在50~8 000 Hz之间[8],时域表达形式如下 g(f,t)=kta-1e-2πbtcos(2πft+φ),t≥0 (5) 式中k为滤波器增益,a为滤波器阶数,f为中心频率,φ为相位,b为衰减因子,该因子决定相应的滤波器的带宽,它与中心频率f的关系为 b=24.7(4.37f/1000+1) (6) 由于Gammatone滤波器的时域表达式为冲击响应函数,所以,将其进行傅里叶变换就可以得到其频率响应特性。语音信号通过该滤波器时,输出信号Gm(i)的响应表达式为 Gm(i)=[|g|(i,m)]1/2,i=0,…,N-1; m=0,…,M-1 (7) 式中N=64为滤波器的通道数,M为采样之后的帧数。这样Gm(i)就构成了一个矩阵,它的每一列称为Gammatone特征系(GF)[9],一个GF特征矢量由64个频率成分组成。由于相邻的滤波器通道有重叠的部分,GF特征矢量相互之间存在相关性。为了减小GF特征矢量的维度和相关性,这里对每一个GF特征矢量进行离散余弦变换(DCT),具体表示为 (8) 将系数Ci(j)称为GFCC系数。在实际的说话人识别系统中,由于计算量大,并非取全部维数的GFCC系数。文献[10]证明,由主成分分析(principalcomponentsanalysis,PCA)技术,可以把64维GFCC系数,按累积贡献率不小于85 %的准则,降到26维。降维后的GFCC特征参数表示为 G(i)={Cj(i)|j=1,…,26} (9) 基于压缩感知的改进小波抗噪识别系统的算法流程如下: 步骤1对带噪语音信号进行预处理,对一帧语音进行多尺度小波分解,得到系数向量Θ。 步骤2计算Θ的Gini系数G(Θ)。若G(Θ)>0.9,取0.8M个观测数,M为常规非稀疏性观测实验所取的观测数,按稀疏度k1修剪小波树,k1的选择由仿真实验中表1确定,若G(Θ)<0.9,取0.4M个观测数,按稀疏度k2修剪小波树。 步骤3利用CSSA算法对原始稀疏向量Θ进行小波树的修剪,对不同观测数目选择合适的小波树节点数量,即该向量的稀疏度。 步骤4对观测信号y进行小波树模型的重构,重构出系数向量,详细步骤如下: 步骤6将重构得到的降噪信号提取特征参数GFCC,然后在高斯混合模型中进行识别。 实验所用的语音库是用麦克风录制的,语音采用的是单声道,8kHz的采样频率,16bit量化。语音库由50个不同年龄段的男女所录制而成,每个人录制10段语音,时长2~5s不等,总共500段。首先研究了一段麦克风录制的语音信号“咖啡”在小波分解下系数向量的稀疏性,对每一帧的多尺度小波分解系数用CSSA算法对小波树修剪并计算其Gini系数,结果如图2。 图2 各帧系数向量的Gini系数分布Fig 2 Gini coefficient distribution of each frame coefficient vector 对于原始向量,第1~5帧及24~28帧处Gini系数较低,表示其稀疏性较差,分析可以发现语音信号这几帧的区间大部分都在声母“k”和“f”的清音部分,其他帧则是在韵母“a”和“ei”的浊音部分,稀疏性较好。 对于小波树模型,保留较少的小波树节点虽然可以提高系数向量的稀疏性,但是却增大了与原信号的误差,在一定观测数目下的压缩重构又需要较好的稀疏性。为此,本文对观测数目和保留的小波树节点数之间关系对重构信号的影响进行研究。分别选取声母“k”“f”和韵母“a”“ei”各取一帧N=512来代表清音帧和浊音帧,结果如表1。 表1 观测数、小波树稀疏度同信噪比关系 分析表1发现在特定的观测数目下,无论是清音还是浊音帧都可以唯一确定一个稀疏度来得到最好重构效果,如表2。 表2 不同观测数下的最佳稀疏度 通过确定特定观测数目下的最佳稀疏度,对整段语音进行基于稀疏性适应的小波树观测压缩重构,对于信息量高的浊音帧采取 个数目观测;对信息量低的清音帧采取 个数目观测。语音段“咖啡”共有10帧清音44帧浊音,相当于对整段语音信号每帧采用 个观测数目。图3对比了本文稀疏性适应观测方法同固定观测数每帧为 非稀疏性适应观测方法的各帧重构信噪比情况。 图3 各帧重构信噪比对比Fig 3 Comparison of reconstructed SNR of each frame 观察图3发现在清音帧部分,本文方法重构信噪比不如非稀疏性方法,但在含有大多数语音信息的浊音帧部分,信噪比远高于非稀疏性方法。计算帧平均重构信噪比,非稀疏性适应方法只有20.23 dB,而稀疏性适应方法达到了23.12 dB,帧平均信噪比上提高了14 %。 最后,选取本文语音库中每个人的4段语音作为训练样本集,用高斯混合模型(GMM)对其训练。另外6段语音作为测试样本集,混入标准噪声库NOISEX—92中的白噪声,信噪比分别为-5,0,5 dB和10 dB,用本文方法对其进抗噪重构,然后通过Gammatone滤波器组提取特征参数GFCC,在GMM模型中进行识别,GMM的混合数为16,结果如图4。可以发现,本文方法的识别率要高于传统非稀疏性适应观测方法。 图4 白噪声下的识别结果Fig 4 Recognition result under White noise 本文给出了一种基于压缩感知的改进小波抗噪识别系统,先对带噪语音信号作预处理,然后经改进小波压缩重构,将重构恢复的语音信号通过Gammatone滤波器组提取特征参数GFCC,最后在GMM模型中识别。该方法有效权衡语音信号稀疏性、观测数目及重构精度。实验结果证明:在相同压缩比情形下,与非稀疏性适应观测方法相比本文有更高的重构信噪比和识别率。虽然小波树模型有较好的稀疏性,但模型较为固定并没从信号本身构造出更好的稀疏域。因此,为特定信号构造一个更好的稀疏变换,同时使用一个快速有效的重构算法仍是以后研究的重点。 [1]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [2]雷颖,钱永青,孙洪.帧间自适应语音信号压缩感知[J].信号处理,2012,28(6):894-899. [3]Baraniuk R G.Optimal tree approximation with wavelets[C]∥SPIE’s International Symposium on Optical Science,Enginee-ring,and Instrumentation,International Society for Optics and Photonics,1999:196-207. [4]Baraniuk R G,Jones D L.A signal-dependent time-frequency representation: Optimal kernel design[J].IEEE Transactions on Signal Processing,1993,41(4):1589-1602. [5]Needell D,Tropp J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321. [6]周小星,王安娜,孙红英,等.基于压缩感知过程的语音增强[J].清华大学学报,2011,51(9):1234-1238. [7]Hurley N,Rickard S.Comparing measures of sparsity[J].IEEE Transactions on Information Theory,2009,55(10):4723-4741. [8]王玥,钱志鸿,王雪,等.基于伽马通滤波器组的听觉特征提取算法研究[J].电子学报,2010,38(3):525-528. [9]Shao Yang,Jin Zhaozhang,Wang Deliang.An auditory-based feature for robust speech recognition[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing,Institute of Electrical and Electronics Engineers,US,2009:4625-4628. [10] Zhang Wanfeng,Yang Yingchun,Wu Zhaohui,et al.Experimental evaluation of a new speaker identification framework using PCA[C]∥IIEEE International Conference on Systems,Man and Cybernetics,2003:4147-4152. Design of improved wavelet anti-noise recognition system based on compressive sensing* MAO Zheng-chong, SHAO Zhu-yu (Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi 214122,China) Allocate observation numbers adaptively,according to sparsity in wavelet tree of speech frames,change number of wavelet tree nodes with different observation numbers.This method solves mismatching problem between the nodes number in the tree model and measurement of speech signal.Denoising the preprocessed speech signal by improved wavelet,then,through Gammatone filters to deal with the enhanced speech signal, extract feature parameters GFCC.Simulation experiment results demonstrate that SNR increases 14 % compared with traditional wavelet method,effectively reduce effect of noise in speech signal and the system recognition rate and robustness are improved obviously. compressive sensing; wavelet denoising; sparsity adapt to observation; anti-noise algorithm; recognition rate 2015—11—04 江苏省自然科学基金资助项目(BK20131107); 国家自然科学基金资助项目(60973095) TP 391.4 A 1000—9787(2016)08—0094—04 茅正冲(1964-),男,江苏启东人, 副教授,研究生导师,主要研究方向为机器人视听觉识别。 DOI:10.13873/J.1000—9787(2016)08—0094—042 Gammatone特征提取
3 算法流程
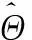
4 实验结果与分析

5 结 论

