城市轨道交通开行方案鲁棒设计及优化

朱小马　孟学雷　雷 明



城市轨道交通开行方案鲁棒设计及优化

朱小马孟学雷雷 明

文章综合考虑乘客的出行成本和城市轨道交通的运营成本，建立城市轨道交通列车开行方案费用模型，运用鲁棒思想对不同时段运营的成本进行分析，并运用遗传算法对该模型进行求解，确定合理的发车间隔、列车的开行频率以及所需要安排的列车数，从而为城市轨道交通运营制定合理的列车开行方案。

城市轨道交通；列车开行方案；鲁棒设计

0　引言

城市客流出行选择具有时段性的特点，例如，早晚高峰时段，中午平峰时段，任意选择其中一个时段客流量作开行方案的制定依据都不够合理，这就需要根据旅客出行时段性进行分析，按时段制定列车开行方案，这样可以提供高质量的运输服务，降低轨道交通的运营成本。本文根据旅客出行弹性需求的特点，对城市轨道交通不同运行时段的客流进行分析。通过鲁棒优化研究，对列车开行方案提出合理建议，提升城市轨道交通服务质量。

1 列车开行方案模型分析

1.1列车开行方案相关概念

影响列车开行方案的因素比较多，国内外学者对开行方案的研究比较成熟，但大多数研究都没有考虑在突发情况时客流波动大的特点下导致列车开行方案的不适应性，本文主要引入鲁棒优化的思想，对开行方案进行优化，从而增加运营公司的利益以及提高列车服务的质量。为简化问题，以一段城市轨道交通线路为研究对象，构造列车线路网络。设该段线路包括 N 个站点，城市轨道交通运行网络构造 G = { V, E }，各站点集合 V = { Vi| i = 1, 2, 3 … N }，路段集 E = { ei| i = 1, 2, 3 …N-1 }，eij表示站点 Vi与 Vj的路段，Lij表示站点 Vi到 Vj的路段距离。

旅客出行成本最小和运营成本最小是互相矛盾的目标，旅客希望运营公司提供开行频率高的服务以减少在站的等待时间，而运营公司考虑到每列车开行的成本比较大以及所需购买动车组比较昂贵，尽量以最少的动车组以及增大发车间隔来满足客流需求。建立旅客出行成本最小和运营公司成本最小的多目标规划模型。

由于客流需求在每个运行时段不是确定的，根据已有的客流统计分析，首先制定某一时段的列车开行方案，确定在该时段列车开行频率。设开行频率为 f ，为了满足旅客的需求，设定开行频率的下限为 f0，列车开行频率的上限值为 f1≤（T / h），T 为运营周期，h 为该周期内发车间隔时间。

城市轨道交通在一天内运营时间一般在早上 5 : 00到晚上 23 : 00，那么在这个运营时间内包含如下的客流时段，如，高峰时段（7 : 00—9 : 00、17 : 00—20 : 00、12 : 00—14 : 00），平峰时段（9 : 00—12 : 00、14 : 00—17 : 00），低峰时段（5 : 00—7 : 00、20 : 00—23 : 00），列车在一个固定时段采用固定的编组且开行的列车辆数一定，假设车辆的载客能力为 Ca，编组长度为 b，将一天内的运营时间分成 K 个运营时段，那么任意一个时间段 Tk内所需要的列车数为 dk，其中 k 为任意的整数且K = { k | k = 1, 2, … , K }。

1.2旅客出行费用分析

旅客的出行成本包括乘坐列车的票价成本以及出行耗费的时间成本。

1.2.1票价成本

假设在第 Tk时段内，在该站列车上人数为 Qi，i 站到 j 站的稳定客流量为 Qij( k )，旅客的票价支出的确定可以按照元 /人· km计算，那么旅客的票价支出成本可以表示为 P票价= σ Lij，其中 σ 为票价率。

1.2.2时间成本

旅客的时间成本又包括候车时间成本和旅行时间成本，旅行时间是指旅客在所需乘车区段列车运行的距离 Lij与列车的平均运行速度 v 之间的比值。旅客的候车成本可以用旅客平均等车时间来表示，也就是列车的发车间隔 h，那么旅客的时间价值成本可以表示为 P时间= η ( Lij/ v + h / 2 )，其中 η 表示为时间价值率。这样，总的旅客出行成本 Z1最小化的目标函数模型可以表示为：

1.3轨道运营公司费用分析

列车开行方案的制定必须要考虑自身的运营效益问题，运营方总倾向于将运营的成本减到最低，但轨道交通作为公益团体，首先必须满足客流的需求。列车的运营收益主要来源于售票的收入，而城市轨道交通票价基本恒定，轨道交通公司的效益主要考虑列车的运营成本，那么使得运营公司成本 Z2最小的目标函数模型为：

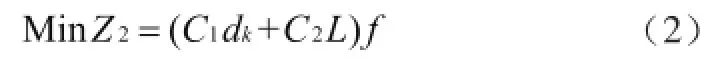
式（2）中，C1为开行该次列车所需的固定成本；C2为列车运行每公里成本； L 为列车运营的公里数。

规划是学校事业发展的指引和目标，指导和规范各类建设项目。学校按照一体化发展思路，以资源共建共享为指导思想，编制了《广东开放大学“创新强校工程”（2016-2020年）发展规划》《广东理工职业学院“创新强校工程”（2016-2020年）发展规划》，对非学历的继续教育明确了建设项目、建设内容、建设任务以及预期取得的成效。

旅客出行总成本 Z1最小和运营公司成本 Z2最小是相互矛盾的目标，综合求解上述式（1）、（2）模型无法得到最优解，这种多目标规划问题只能通过智能算法或是化成单目标问题求解。对于单目标形式求解，本文首先根据目标的相对权重设置影响因子 α 和 β，α 表示旅客总成本的权重，β 表示运营公司成本的权重，且 α + β = 1，最后本文将多目标化成单目标的最小化成本 Z 函数模型为：

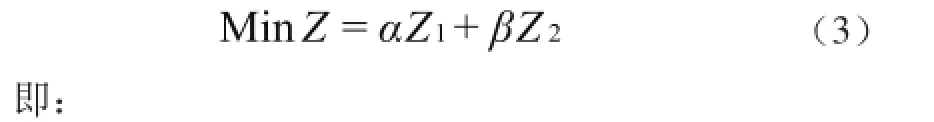
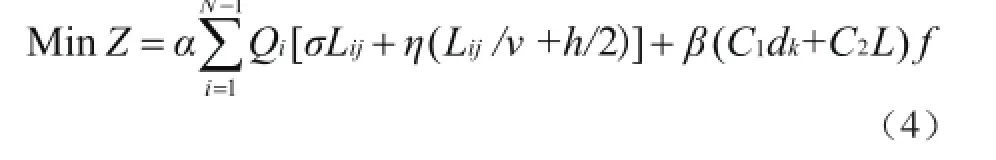
2　开行方案鲁棒设计模型

由于不同的运营时段旅客到达是不均衡的，且具有一定的随机性，所以需要根据旅客客流波动的特点制定合适的列车开行方案。假设某一时段，从 i 站到 j 站的客流在以 h 为发车间隔内到达 j 站服从泊松分布，到达的概率为 pij( λk)，那么在该站聚集的旅客人数则为 Qi：

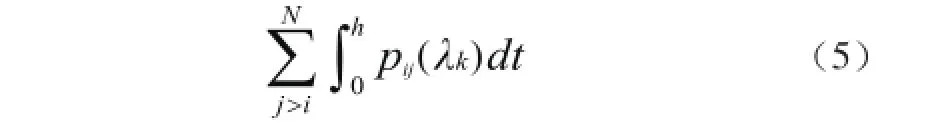
此情况下总的成本 Z 最小函数模型为：

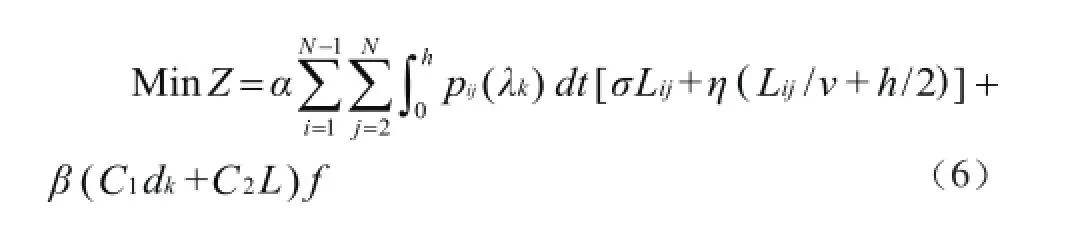
根据客流统计分析，某一时段在整个统计数据中该客流时段出现的概率为 θk，那么在发生客流波动的情况下，适应该客流时段客流波动下总成本 Z 最小的鲁棒开行方案模型为：

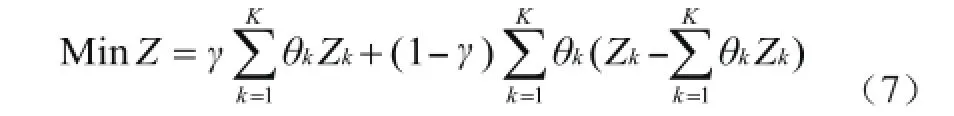
式（7）服从于约束条件（8）～（12）：

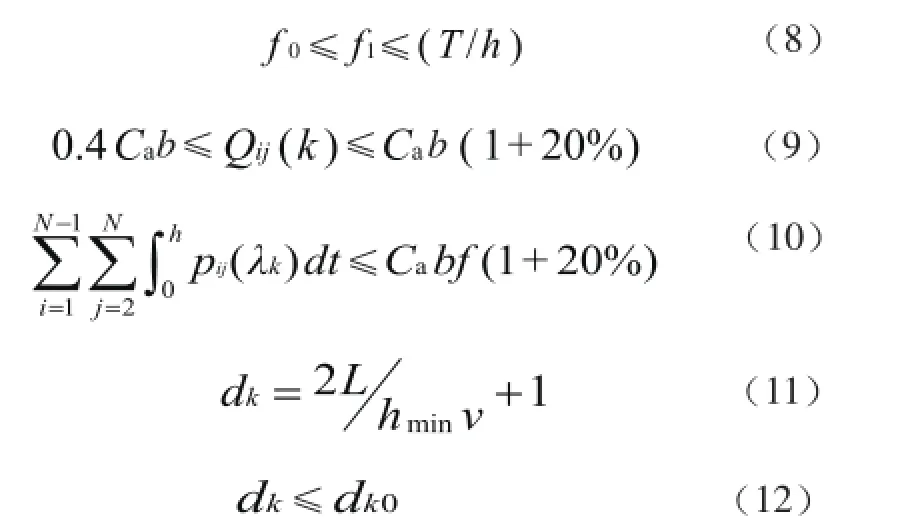
式（8）表示列车的开行频率要满足旅客出行需要不得小于 f0，而且不得大于周期和频率的比；式（9）表示 i 站到 j 站车厢内的旅客人数不能低于一定的载客量也不能超过车厢的最大载客量；式（10）表示一个周期内开行的旅客列车服务次数能运送这段时间内在各个站聚集的旅客人数；式（11）、（12）表示在运营周期内一个时段所需的列车辆数，且在客流最大波动下的运营的列车数量 dk不能大于轨道交通公司拥有的列车数量 dk0。

3 算例分析及改进遗传算法求解

3.1算例

引入一条城市轨道交通线路，假设某城市轨道线路如图 1 所示，线路总长度为 14.7 km，共设有 8 个车站。运营时段为早上 5 : 30 到晚上 11 : 30，列车的运营周期为60 min，列车运营平均时速为 65 km/h。列车均采用8节车厢编组，每节车厢能容纳的旅客人数为 65 人。不同时段旅客在各站进站的概率分别为 λ高峰= 8，λ平峰= 5，λ低峰= 4，旅客的票价率为 σ = 0.8 元 / km，时间价值率η = 0.6 元 / min。列车开行的固定成本 C1= 75 元 / 辆，运营成本 C2= 15 元 / km，旅客总成本的权重和运营公司的权重分别为 α = 0.45，β = 0.55。

图1　线路及车站示意图

（1）构造解空间。这里的解空间可以用发车间隔 h 来表示，为了便于计算，发车间隔 h 可以取值为2.5、3、3.5、4、4.5、5、5.5、6、6.5、7.5、9、10 min。这些发车间隔都满足约束条件（8），那么 3 个时段不同发车间隔的解为上述发车间隔的随机组合。采用实数编码的形式对解的空间进行编码，如编码的形式为（ 2.5，3，3.5 ）则分别表示一天内高峰时段、平峰时段、低峰时段的发车间隔。

（2）适应度计算。上述发车间隔构成的染色体，有些染色体在解码后不符合约束条件（9）、（10）、（12），那么这些染色体为不可行染色体。为了使解码后满足所有的约束条件，在生成初始解时剔除不符合条件的基因个体，交叉变异过程中生成的这些不可行染色体要重现生成。对于可行的染色体需要计算它的适应度，适应度函数 F 可以表示为：（13）

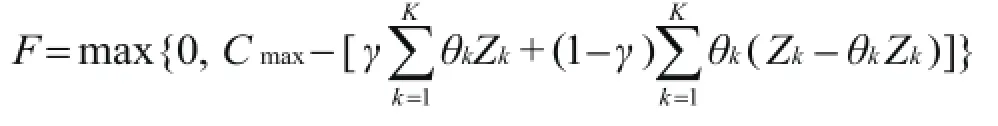
由于涉及到随机变量 θk，需要根据客流统计采用随机模拟计算适应度。

（3）选择。对个体进行优胜劣汰，适应度高的个体将被遗传到下一代，适应度低的将被淘汰。在算子选择的过程中，采用最优保存策略进化模型，首先找出当前群体中适应度最高的个体和适应度最低的个体，保留当前种群中最佳个体的适应度，并与此前最佳个体适应度相比较，选择最优的个体替换当前种群的中最差的个体。

（4）交叉和变异。均采用单点操作模式，根据交叉和变异的概率选择染色体，将染色体的某一相同位置基因进行交换和变异操作。

3.3算例结果

根据遗传算法求解的结果，可得出在不同时间段的发车间隔组合为（3.5，6，8.5），即在高峰时段的发车间隔为 3.5 min，平峰时段发车间隔为 6 min，低峰时段发车间隔为 9 min，最小所需运营车辆数为 8 辆的情况下，能够使得旅客的总出行成本以及轨道交通运营公司的成本最小，这种发车间隔组合能够应对在不同情境下符合客流波动情况的列车开行方案。

4　结束语

本文通过分析客流的需求特性，构建了在不同客流时段的城市轨道交通运营公司运营成本和总的旅客出行成本的最小化模型，引用鲁棒的思想来克服每一天客流波动的随机性，最后得出的结果能很好地指导运营公司制定合理的列车开行方案，同时也为运营公司购买列车辆数量提供了依据。

[1] 邓连波，曾强，高伟. 周文梁基于弹性需求的城市轨道交通列车开行方案研究[J]. 铁道学报，2012，34（12）.

[2] 史峰，周文梁，陈彦，等. 基于弹性需求的旅客列车开行方案优化研究[J]. 铁道学报，2008，30（3）.

[3] 牛惠民，陈明明，张明辉. 城市轨道交通列车开行方案的优化理论及方法[J]. 中国铁道科学，2011，32（4）.

[4] 汪波，杨浩，张志华. 基于周期运行图的津京城际铁路列车开行方案研究[J]. 铁道学报，2007，29（2）.

[5] 赵钢，彭其渊. 城际铁路列车开行方案优化分析[J].交通科技与经济，2008（6）.

[6] 孙鹏，赵佳虹，丁宏飞. 基于换乘协调的城市轨道交通列车开行方案优化[J]. 铁道运输与经济，2011，33（12）.

[7] 孟学雷，贾利民，卜萌，等. 基于决策偏好可控的地铁列车开行方案设计研究[J]. 铁道科学与工程学报，2012，9（1）.

Robust Design and Optimization of Transit Operational Plan

Zhu Xiaoma, Meng Xuelei, Lei Ming

The paper makes a comprehensive consideration on the passenger travel cost and urban rail transit operating costs, having established a train operational plan cost model for urban rail transit, making an analysis by using the robust concept on the cost of operations in different time slots, and also using genetic algorithm to solve the model, determining the reasonable departure intervals, train running frequency and the need to arrange the number of trains, thus it provides reasonable train operational plans for urban rail transit.

urban rail transit, train operational plan, robust design

论坛园地

U293.1

朱小马：兰州交通大学，硕士研究生，甘肃兰州 730070

国家自然科学基金项目：基于复杂网络的列车运行图稳定性优化研究（61263027）

2015-07-02责任编辑 朱开明