探究《解直角三角形的应用》讲解方法

宋成学

新疆生产建设兵团第六师教育局教研室



探究《解直角三角形的应用》讲解方法

宋成学

新疆生产建设兵团第六师教育局教研室

利用解直角三角形来解决实际问题在新疆初中学业水平考试中的出题频率很高，分值也较大，因此，解直角三角形可以说是初中阶段的考察的一个重要的内容。对于学生来说，这是必须让学生掌握的。而对于老师来说如何对本知识点进行讲解，是值得进行研究的。解直角三角形的重点是让学生学会数学思想。数学思想是解决数学问题的灵魂，在初中数学中蕴含着丰富的数学思想方法，需要我们去挖掘并应用于解题过程。本节所用的数学思想有：分类思想、方程思想和转换思想。分类思想，就是当被解决的问题包含两种或两种以上的可能情况时，则需要按不同的情况分类来解决的一种思想方法；方程思想是一种重要的解题思想方法，在解决与直角三角形和相似三角形有关计算问题，往往从问题中构造方程，通过解方程解决问题；转化思想是数学问题的一种重要的思想方法，转化思想把未知的转化为已知的、把抽象的转化为具体的、把一般转化为特殊等等，都是转化思想的重要体现。

《解直角三角形的应用》一节共需两个课时，但如何利用这两个课时让学生很好的掌握本节知识，这需要教师对本节课进行典型事例汇总，总结出本节在中考中常考题型的演变和典型图形。对于解直角三角形的考题而言，大多都是双直角三角形的习题，双直角三角形是指一条直角边重合，另一条直角边共线的两个直角三角形。解这类问题的基本思路是：运用“遇斜化直”的数学思想，即通过作辅助线（斜三角形的高线）把它转化成为双直角三角形问题，然后根据已知条件与未知元素之间的关系，利用解直角三角形的知识来求解下面就如何对本节知识点进行整合谈谈自己的观点。

一、第一类典型例题分析

人教版九年级数学下册第28.2.2应用举例中共给出了两个例题，其中比较重要的是第二个例题：

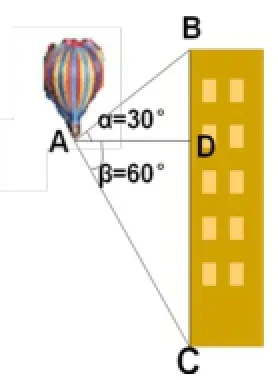
例题：热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，热气球与高楼的水平距离为120m，这栋高楼有多高？

本题考察的是题中有两个直角三角形时的分析方法，这类题型的掌握对学生后期的学习和训练提供的很多帮助，因为，很多情景和题型都是有本题演变而来。

例如：第76页的例5：如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（结果取整数）

如果教师在讲解中把第一个例题讲解透彻，作为典型图例模型，让学生理解分析这种图例的结题方法，那么，76页的例5，学生就会自己轻松的解决，因此，我们在教学中，总结第一个解直角三角形的应用典型图例模型一：

本模型有两种设问方式：（1）已知AB和两个角，求BD；（2）已知AC和两个角，求BD。

二，第二类典型例题分析

通过例题来总结图例模型是一种对教材整合的方法，但除了例题，教材中的练习题我们也不能忽视。例如，教材第76页的练习1：

如图，建筑物BC上有一旗杆AB，由距BC40m的D处观察旗杆顶部A的仰角为50°，观察底部B的仰角为45°，求旗杆的高度。

这一试题的图例特征也是我们在试卷中经常见到的一种，它的情景不仅仅是在测量建筑物的高度上，在航海航空方面的习题中也是经常见到的，例如课本教材第77页的练习第一题：海中有一个小岛A，它的周围8海里范围内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏东30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？

这个图例的设问情景有很多，再比如测量类的：某中学九（2）班数学活动小组利用周日开展课外实践活动，他们要在湖面上测量建在地面上某塔AB的高度.如图3，在湖面上点C测得塔顶A的仰角为45°，沿直线CD向塔AB方向前进18米到达点D，测得塔顶A的仰角为60°.已知湖面低于地平面1米，请你帮他们计算出塔AB的高度（结果保留根号）。

这类试题的分析也主要是围绕解两个直角三角形来进行的，但在解直角三角形的过程中运用了方程的思想，比如最后一题的解题方法为：延长CD交AB的延长线于E，则AE⊥CE。

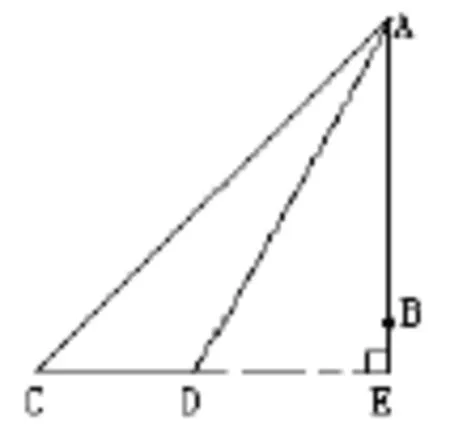
设AB=x，在Rt△ADE中，因为AE=x+1，∠AED=60°，

在Rt△ACE中，因为∠C=45°，所以CE=AE=x+1，

通过设塔构造方程解决问题，使问题易于理解.同时本题也体现了一种建模思想.因此，我们可以把这类试题图例作为第二个典型模型进行讲解。

通过这两个典型图例模型的讲解，可以比较系统的让学生掌握利用解直角三角形来解决实际问题的方法。遇到类似的问题，可以引导学生巧妙的作出辅助线，将问题转化成这两个典型图例模型，从而，达到学生自己解决问题的目的，也体现了数学建模中将未知问题转化成已知问题的基本思想。