“圆”中错解,你有过吗?
赵萍萍
“圆”中错解,你有过吗?
赵萍萍
圆的学习,概念繁多,性质与判定交叉复杂,不少定理又有限制条件或前提条件,而且圆还具有多种对称性质,使得与圆有关的角、弦等位置关系充满着多种可能性,初学圆或综合起来解圆的习题时,有些同学就容易混淆概念或忽略不同情形,造成漏解、错解,下面我们做一些易错题盘点.
易错点1一条弦所对圆周角的值有两个,忽略其中一个
例1在半径为r的圆内,求长为r的弦所对的圆周角.
【错解】如图1所示,⊙O的半径为r,AB= r,∠ACB为弦AB所对的圆周角,连接OA,OB,则OA=OB=AB=r,
∴△OAB为等边三角形,
∴∠AOB=60°,
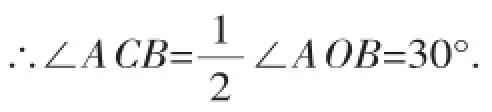

图1
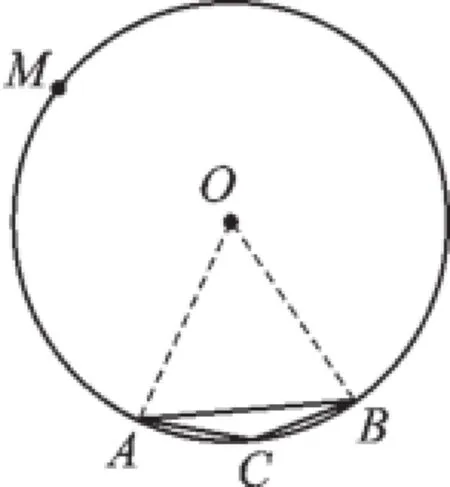
图2
【错解分析】产生错解的原因是只考虑了长为r的弦所对的圆周角的顶点在优弧上,却忽略了圆周角的顶点在劣弧上的情况.
【正解】如图1,当圆周角的顶点在优弧上时,同上;如图2,当圆周角的顶点在劣弧上时,∠ACB=180°-30°=150°.
易错点2证明切线时理由不充足,表达不规范
例2 如图3,已知△ABC中,∠C=90°,AC=BC,D,E分别是AC,BC的中点,⊙O是△DCE的外接圆.求证:AB是⊙O的切线.
图3
【错解】连接CO并延长交直线AB于F,
∵AC=BC,D,E分别为AC,BC之中点,
∴DC=EC=AD=BE,
∴DE∥AB,
∴O为CF中点,即有OF=OC,
∴AB为⊙O的切线.
【错解分析】证明中虽有OF=OC,但没有说明OF是圆心到直线的距离,理由不充足.
【正解】连接CO并延长交直线AB于F,
∵∠C=90°,∴DE为直径,点O在DE上.
∵AC=BC,D,E分别是AC,BC的中点,
∴CD=CE,DE∥AB,
∴O为CF中点,即OC=OF.
∵DE为⊙O的直径,OD=OE,
∴CO⊥DE,
∴OF⊥AB,
故AB为⊙O的切线.
易错点3当两圆相切时,只考虑一种情况造成漏解
例3半径分别为1 cm和2 cm的两圆外切,那么与这两圆都相切且半径为3 cm的圆的个数有().
A.2个B.3个
C.4个D.5个
【错解】A或C.
【错解分析】错选A的原因是只考虑所求圆与已知两圆外切的情形;错选C的原因是考虑所求圆与已知两圆都外切的情形,以及与其中一圆内切、另一圆外切的情形,漏掉了与两圆都内切的情形.所求圆与已知两圆的位置关系有五种情形:与两个圆都外切,符合条件的圆有两个;与其中一个内切,另一个外切,符合条件的圆也有两个;与两个都内切,符合条件的圆只有一个.
【正解】D.
易错点4滚动问题中弧长的计算出错
例4一个小朋友在粗糙不滑动的“Z”字型平面轨道上滚动一个半径为10 cm的圆盘,如图4所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60 cm,CD= 40 cm,BC=40 cm,请你作出该小朋友将圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度.

图4
【错解】此路线的长度为AB+BC+CD= 60+40+40=140(cm).
【错解分析】如图5所示,圆盘在滚动过程中圆心经过的路线由四段组成,第一段:线段OO1,第二段:线段O1O2,第三段:O2到O3的一段圆弧,第四段:线段O3O4.显然路线长度不是线段AB、BC、CD的长度之和.
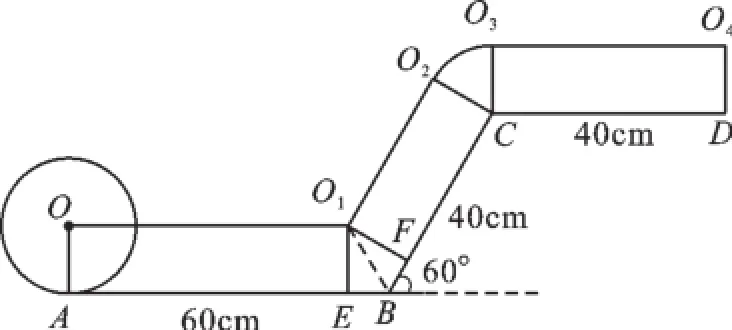
图5
【正解】由点O1分别作O1E⊥AB,O1F⊥BC,可得∠O1BE=∠O1BF=60°,
在Rt△O1BE中,
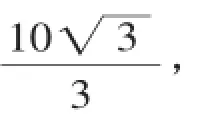
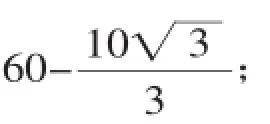
由BE=BF得,
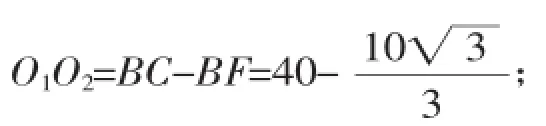
由∠O2CO3=360°-120°-2×90°=60°,
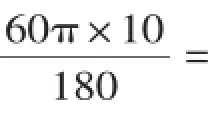
O3O4=CD=40.
所以,圆盘从A点滚动到D点其圆心所经过的路线的长度是
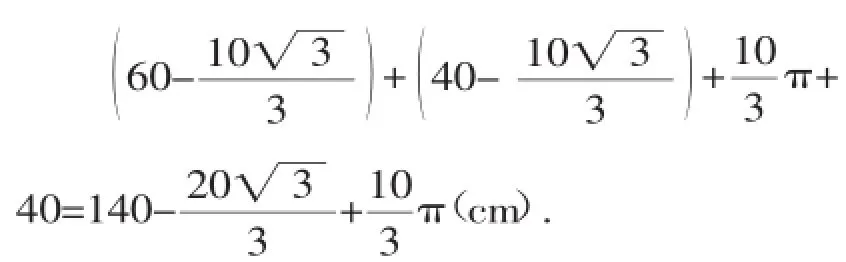
小试身手
1.(2015·黑龙江)如图6,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是().
A.60°B.120°
C.60°或120°D.30°或150°
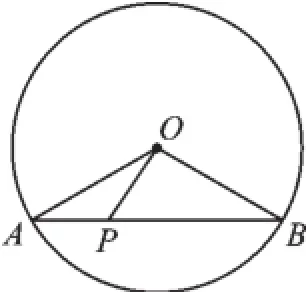
图6
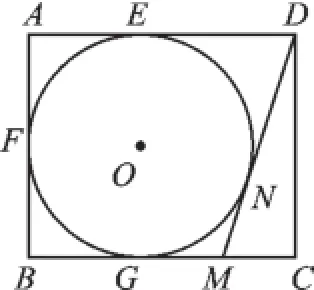
图7
2.(2015·南京)如图7,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为().
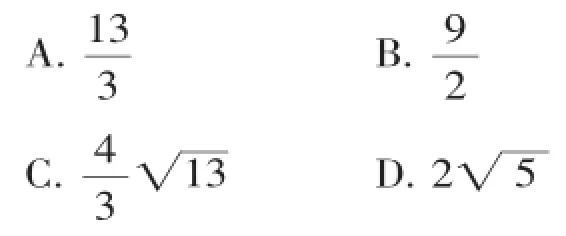
参考答案
1.C
2.A解:如图8,连接OE,OF,OG,
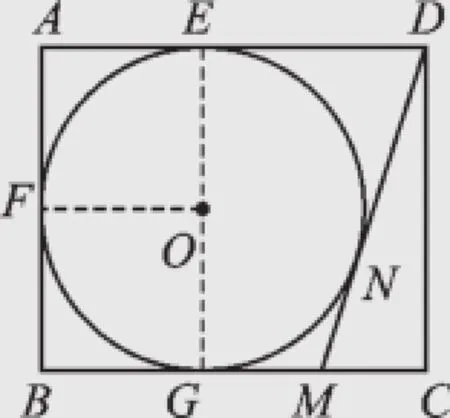
图8
则根据矩形和切线的性质知,四边形AEOF,FOGB都是正方形.
∵AB=4,
∴AE=AF=BF=BG=2.
∵AD=5,
∴DE=DN=3.
设GM=NM=x,
则CM=BC-BG-GM=3-x,DM=DN+NM= 3+x.
在Rt△CDM中,由勾股定理得:
DM2=CD2+CM2,即(3+x)2=42+(3-x)2,
故选A.
(作者单位:江苏省南通市第一初级中学)

