基于贝叶斯网络的罐式汽车运输风险分析*

陈琳 谢学飞

（长安大学）

在我国罐式汽车成为液体和气体危险货物道路运输的主要承载工具，由于运输环境的复杂性及运输货物的危险性很容易发生道路运输事故。现在交通安全问题越来越受到人们的重视，随着计算机技术和智能技术的不断发展，为事故分析提供了很大的技术支持。因为引起罐式汽车运输风险的因素是不确定性的，所以有必要对罐式汽车道路运输风险进行定量分析，计算其发生概率，找出引起事故发生的最可能因素，为事故预防提供理论依据。与传统的统计方法和故障树方法相比，贝叶斯网络是一种处理不确定性事件并进行概率推理的重要工具，它能够更好地反应事故发生的不确定性和相关性[1]。能对引发事故的原因进行影响力排序[2]，并通过对交通事故态势的研究验证了该法的有效性[3]。文章提出利用贝叶斯网络模型对罐式汽车进行运输风险分析，得到事故发生概率及导致事故发生的最可能因素，为保障运输安全提供参考。

1 罐式汽车运输事故贝叶斯网络模型的建立

1.1 贝叶斯网络概述

贝叶斯网络是综合利用概率论和图论对不确定事件进行分析和推理的工具，用符号B（G，P）来表示[4]。G表示有向无环图，P表示条件概率表，分别对应问题领域的定性描述和定量描述。在贝叶斯网络模型中，每个节点变量可以是任何问题的抽象，用来代表感兴趣的现象、部件、状态或属性等；连接节点之间的有向边用来表达各个变量之间的相互依赖关系，有向边的箭头代表因果关系的方向性。条件概率表示各个信息要素之间的影响程度。对于根节点来说，它的概率分布称为先验概率。

1.2 基于故障树的贝叶斯网络模型的建立

罐式汽车在运输危险货物的过程中难免会因为各种原因发生事故，虽然这属于小概率事件，但如果一旦发生事故，导致危险品泄漏，将对人员和周围环境造成严重的后果。在构建罐式汽车运输事故泄漏故障树时，首先要分析货物在运输过程中存在的风险因素。罐式汽车发生泄漏主要是由交通事故和非交通事故造成的，而引发这2种交通事故的因素又有很多[5]。文章以罐式汽车发生事故为顶事件，事故的分类为中间事件，具体事故原因为底事件，由上到下，逐步找出导致事故发生的所有原因，建立故障树模型（故障树是一种倒立的树形逻辑关系结构），如图1所示，为了降低计算复杂度，忽略了一些次要因素。

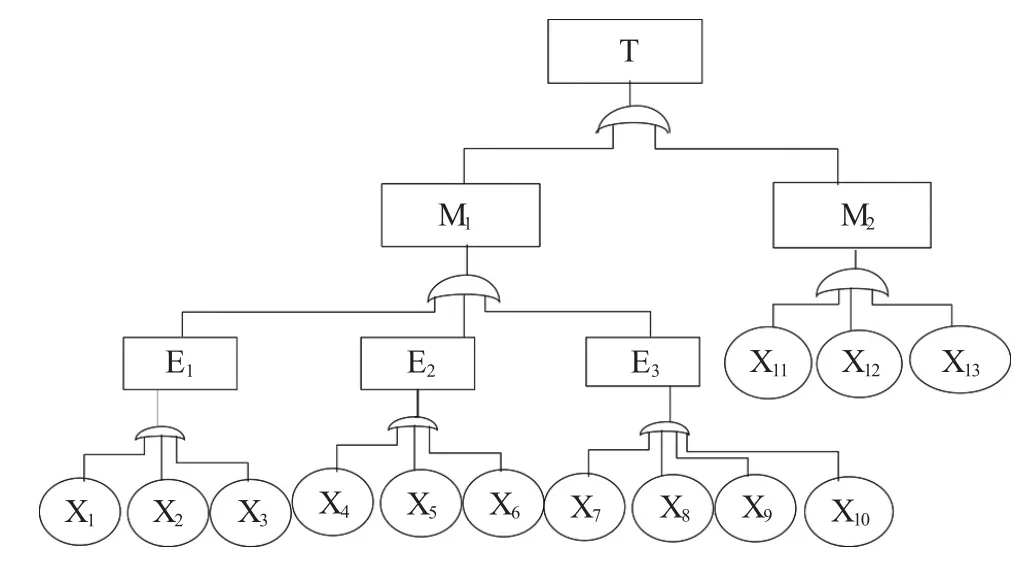
图1 罐式汽车运输事故故障树模型

故障树模型仅仅是对罐式汽车事故进行了定性分析，可以直观地了解引起事故的原因。罐式汽车危险货物运输事故常常是由运输货物自身不稳定性和交通事故引发的，因此罐式汽车危险货物运输事故较普通货物运输事故有更为显著的随机性和易发性。精确的事故概率计算是准确定量评价事故风险和选择最优运输路线的前提，为了进一步进行故障树的定量分析，文章把故障树模型转化为贝叶斯网络模型，将故障树的顶事件、中间事件和底事件分别对应到贝叶斯网络的叶节点、中间节点及根节点，将故障树中底事件的失效概率转化为贝叶斯网络根节点的先验概率；然后根据故障树中各事件的连接关系，将贝叶斯网络中各节点之间用有向边连接起来；最后根据故障树中的逻辑门（与门、或门）关系，获得贝叶斯网络相应节点的条件概率表。这样通过计算贝叶斯网络中叶节点（T）的发生概率及各个根节点的后验概率就能更好地分析事故发生的原因。根据故障树与贝叶斯网络的转换关系，把罐式汽车运输事故故障树图1转化为贝叶斯网络模型，如图2所示。

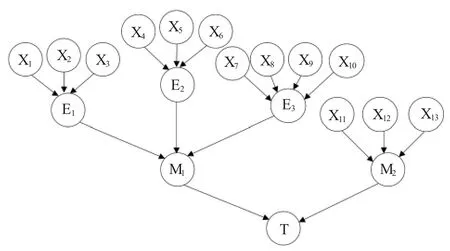
图2 罐式汽车运输事故贝叶斯网络模型

2 罐式汽车运输风险分析

2.1 先验概率与条件概率表的获得

为全面掌握我国罐式汽车运输危险货物的事故特征，系统分析事故发生的机理，需深入探究事故发生的时间、空间、类型、道路等级、诱发原因及泄漏概率等分布规律，为预防事故及保障安全运输危险货物提供理论和数据支持。通过查阅文献、网络搜集、实地调查、勘测和利用各种数据系统整理了2003年1月～2010年12月间发生在中国大陆的886起罐式汽车道路运输危险品事故，并通过对事故发生概率统计结果的分析，得到贝叶斯网络中各个根节点的先验概率，如表1所示。

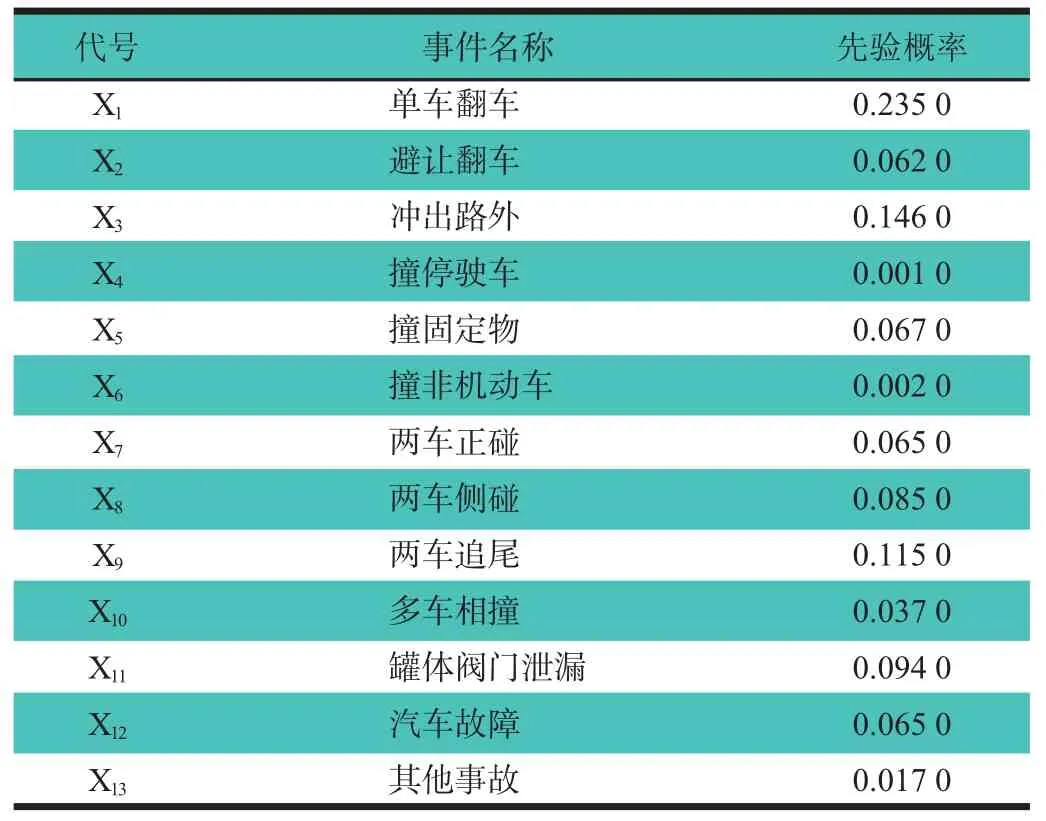
表1 罐式汽车贝叶斯网络根节点先验概率表

根据故障树与贝叶斯网络的转换方法，得到贝叶斯网络中各个节点的条件概率，如表2～表4所示。由于E2，M1，M2的条件概率表与E1相同，故此处省略。表2～4 中：“0”表示事故不发生，“1”表示事故发生。

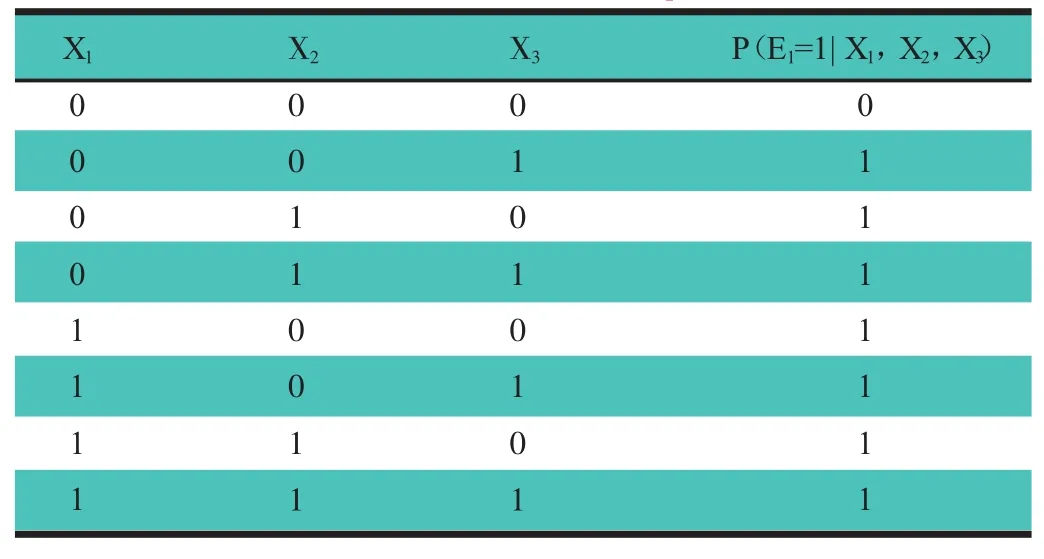
表2 罐式汽车贝叶斯网络中间节点（E1）的条件概率（P）表

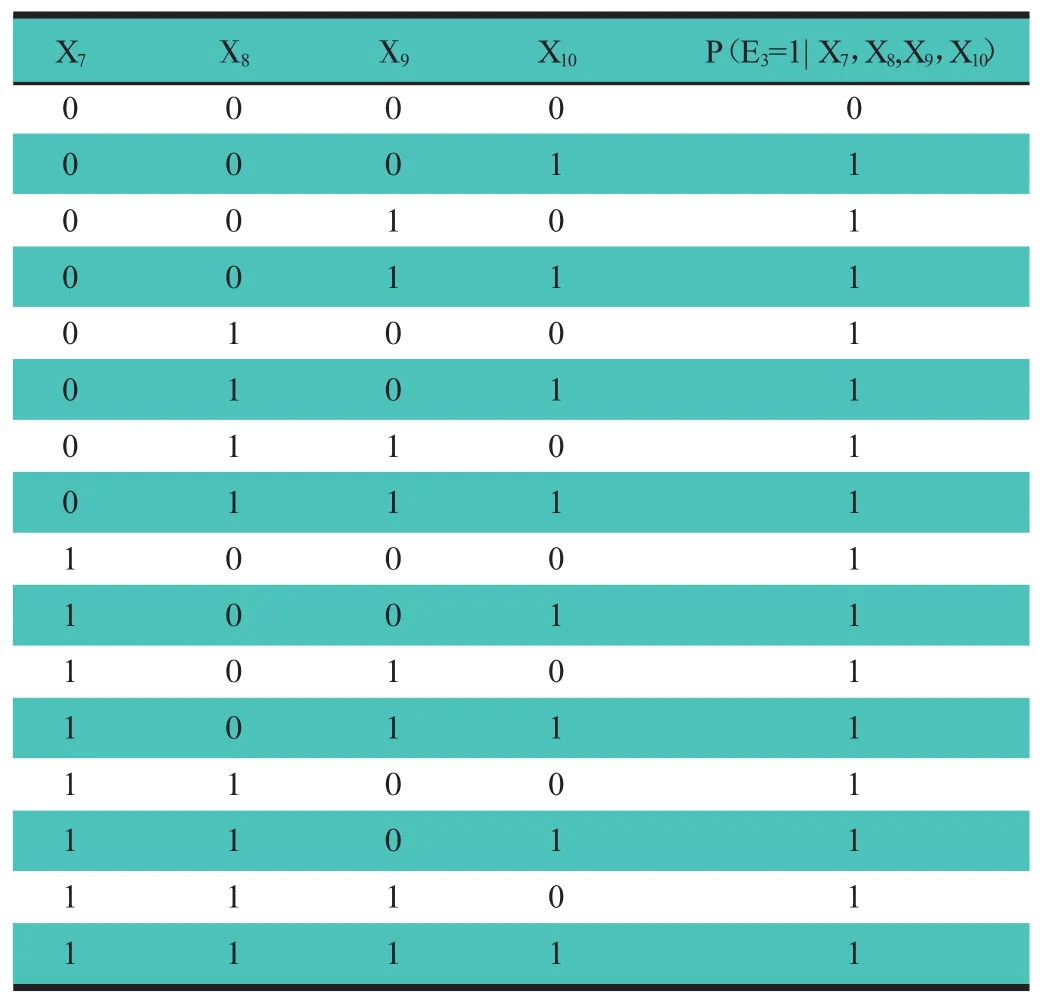
表3 罐式汽车贝叶斯网络中间节点（E3）的条件概率（P）表

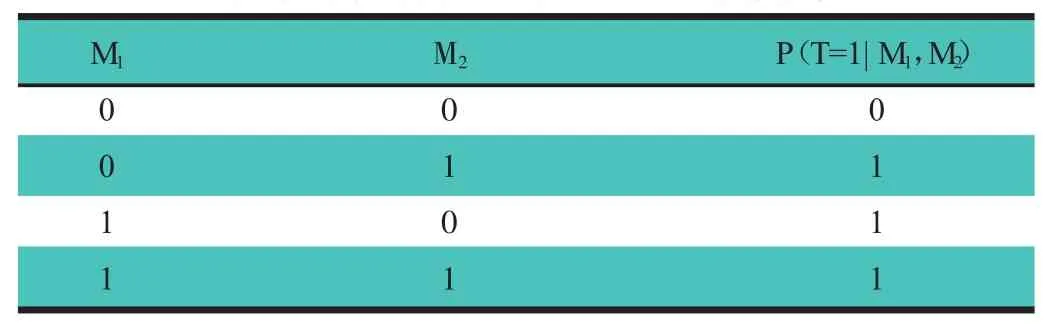
表4 罐式汽车贝叶斯网络叶节点（T）的条件概率（P）表

2.2 贝叶斯网络的概率计算

贝叶斯网络推理的核心任务是计算后验概率，后验概率一般是指通过调查和试验等方法获取了新的信息后，利用贝叶斯公式对先验概率进行修正而得到的更符合实际情况的概率。在用贝叶斯网络计算后验概率时，需要进行贝叶斯公式反向推理，即先假定在某个时刻罐式汽车发生事故，然后通过计算得到各基本事件的后验概率。

由于罐式汽车发生事故的贝叶斯网络较复杂，且计算量较大，通常利用贝叶斯网络工具箱（BNT）对其进行计算，并进行可靠性评估。基于MATLAB的BNT是一个很灵活的工具[6]，它提供了贝叶斯网络学习的底层基础函数库，支持多种类型的概率分布、参数学习和结构学习、近似推理和精确推理及动态模型和静态模型，只需在MATLAB中编程即可计算得出所需节点的概率。

根据获得的先验概率和条件概率，在MATLAB软件中编写程序计算出叶节点（T）发生事故的概率及各个根节点的后验概率。T的发生概率为：P（T=1）=0.657023，中间节点 M1，M2，E1，E2，E3的发生概率分别为：P（M1=1）=0.588 119，P（M2=1）=0.167 291，P（E1=1）=0.387 195，P（E2=1）=0.094 365，P（E3=1）=0.270 875。各个根节点的后验概率，如表5所示。通过后验概率可以找出导致罐式汽车发生事故的最重要因素，这是故障树法所不具有的优势。

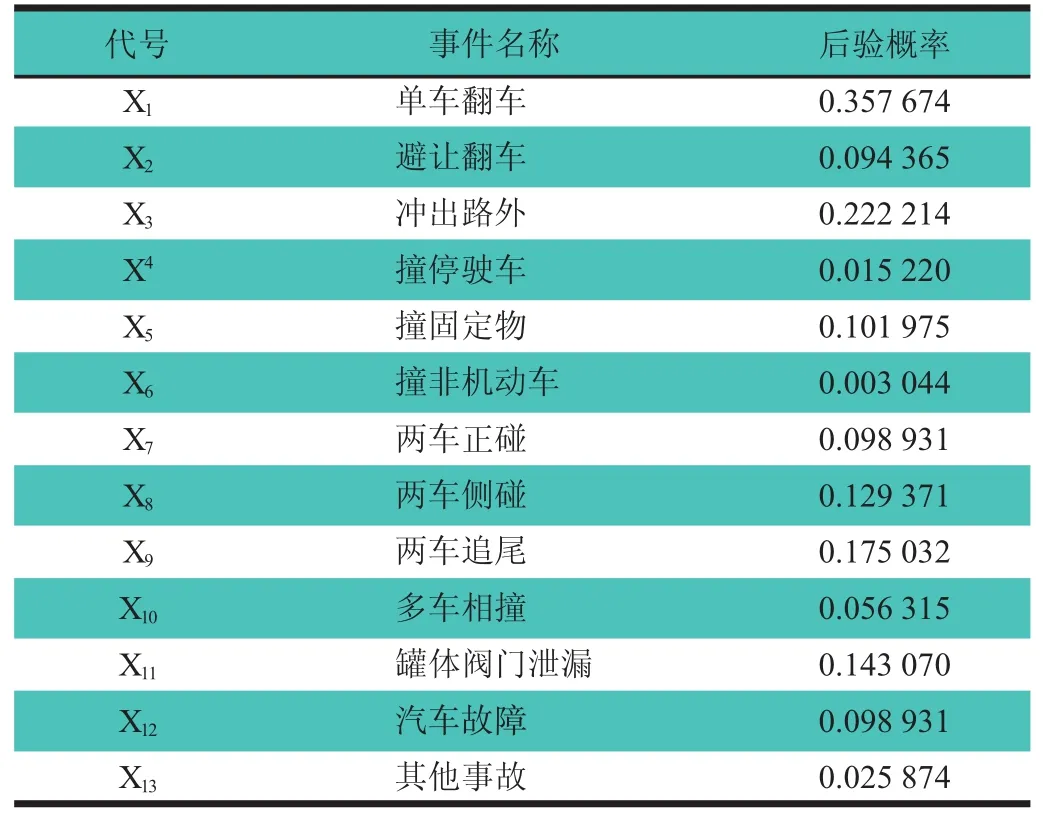
表5 罐式汽车贝叶斯网络根节点（X1～X13）的后验概率表

从T发生的概率来看，罐式汽车在运输气体或液体危险货物时，发生事故的概率达到65.70%，反映了其发生事故的可能性较高。因为后验概率越大，对事故发生的影响越大[7]。由表5可知，单车翻车的后验概率最大，也就是说交通事故引起罐式汽车在运输气体或液体危险货物时发生事故的概率最大。所以罐式汽车在运输危险货物时，应注意防范，避免发生交通事故，导致单车翻车。

3 结论

罐式汽车是液体和气体危险货物运输的主要承载工具，只有在客观因素（如道路、气候及汽车等）状态良好的时候，驾驶员加强警惕，避免交通事故的发生，防止危险货物的泄漏，才能保证周围环境和居民生命财产的安全。通过对886起罐式汽车危险货物运输事故引发的原因等深入分析，获得了山区道路危险货物运输事故产生的机理和主要影响因素，为定量计算风险提供理论依据和数据支持。通过应用贝叶斯网络对故障树进行转换，实现定量计算，找出了引起事故发生的最可能因素是发生单车翻车事故。应用贝叶斯网络分析法不仅可以得到罐式汽车运输事故发生的概率，还能得到叶节点发生时，各个根节点发生的概率，也就是后验概率，从而找出导致事故的最重要因素，这是单一的故障树方法不具备的优势，可应用于事故诊断领域。当然，贝叶斯网络也存在自身的不足和局限性，为使其更好地应用于系统故障分析中，应将贝叶斯网络的算法进行优化，利用动态贝叶斯网络[8]进行分析等。