顺层斜坡溃屈机制与早期识别研究*

汤明高　马　旭　张婷婷　黄润秋　李九乾

(①地质灾害防治与地质环境保护国家重点实验室(成都理工大学)　成都　610059)(②四川省交通运输厅交通勘察设计研究院　成都　610017)



顺层斜坡溃屈机制与早期识别研究*

汤明高①马旭①张婷婷①黄润秋①李九乾②

(①地质灾害防治与地质环境保护国家重点实验室(成都理工大学)成都610059)(②四川省交通运输厅交通勘察设计研究院成都610017)

本文采用物理机制模型、数值模拟和理论计算相结合，分析研究了顺层斜坡滑移—弯曲变形机制，提出了顺层斜坡产生滑移—弯曲变形的地质和力学条件、临溃状态判别与早期识别标志。研究认为：岩层倾角>20°是滑移—弯曲变形产生的必要地质条件。斜坡前缘岩层弯曲隆起是临溃状态的早期判识标志。岩层倾角、单层厚度、临界坡长和溃屈深度之间相互制约和影响。岩层倾角越大，越易产生溃屈，且溃屈层数和深度越大； 斜坡临界坡长与岩层倾角呈负幂函数变化规律； 层间黏结作用产生的共弯效应影响弯曲岩层的整体抗弯刚度，从而制约溃屈深度并对斜坡最终溃屈状态起着决定性作用。该成果对于早期防范和识别地质灾害具有重要价值。

地质灾害顺层斜坡溃屈机制早期识别底摩擦试验数值分析

0　引　言

顺层岩质斜坡是一种常见的斜坡类型。从斜坡结构来看，易产生滑动变形，是岩质斜坡中危害最大的一类(孙广忠， 1988； 黄润秋等， 2007)。其变形模式主要有3种： (1)顺层—滑移，当斜坡前缘完全临空时产生，其形成条件和机制较简单，容易判别。(2)切层—滑移，当未完全临空时前缘岩体被剪断而发生。(3)滑移—弯曲(也称为溃屈)，其形成条件和机制较复杂，具有隐蔽性，因此造成巨大生命财产损失的不乏实例，而且多为大型滑坡，如黄河上游李家峡水电站坝前左岸的2#滑坡、雅砻江二滩水电站坝前的霸王山古滑坡、三峡库区范家坪滑坡、成昆线上的铁西古滑坡、湖北秭归的鸡鸣寺滑坡等。对于溃屈型滑坡，不少学者(Li et al.，1990； 李树森等， 1995； 任光明等， 1998)通过变形机制分析认为会经历3个主要阶段：滑移—轻微弯曲→强烈弯曲—隆起→滑面贯通—整体失稳。也有学者(严明等， 2005)认为在整体失稳之前存在一个中间状态(碎裂—散体化)。如果从变形破坏特点来看碎裂—散体化尚属于强烈弯曲—隆起阶段。同时以孙广忠(1988)为代表的学者采用压杆稳定理论进行了稳定性分析，此后研究者(Wang， 1998； 刘小丽等， 2002； 蒋良潍等， 2006； 冯君等， 2010)基于能量法的弹性板(梁)理论、弹塑性板的翘曲理论等，通过理论推导建立了失稳破坏的力学判据。但是理论计算对地质原型进行了大量简化，不能很好地与斜坡变形机制相结合，其在推导过程中基于假设而建立的数学公式，具有一定的理论价值，但尚难以准确的表述其复杂的地质力学过程。对于机制与力学计算分析相结合的问题，刘钧(1997)认为顺层斜坡是在纵、横力联合作用下而产生的弯曲变形破坏。魏玉峰等(2009)在分析苗家坝水电站何家滑坡成因机制时也有述及，但均未作深入分析。本文认为斜坡溃屈破坏(滑移—弯曲)是斜坡演化过程中产生的顺坡向应力和垂直坡面应力共同作用的结果，因此将斜坡机制分析与压杆、弹塑性梁(板)理论分析相结合，可以相互弥补其局限性。于是采用物理机制模型试验、数值模拟和理论计算分析相结合的方法，进一步探讨了中缓倾外顺层斜坡溃屈机制，特别是查明了其关键状态，通过控制和影响其溃屈破坏的关键因子及其相互作用关系分析，提出了中缓倾外顺层斜坡溃屈破坏的早期识别指标和标志，对于防灾减灾具有重要价值。

1　滑移—弯曲的斜坡地质模型

通过滑移—弯曲型典型滑坡实例分析，建立了地质模型(图1)，主要地质特征如下：

图1　滑移—弯曲斜坡地质模型Fig. 1　Geological model of buckling of bedding slope

(1)岩层倾角：倾角范围15°～50°； (2)岩层厚度：厚度范围0.2～2.0m； (3)斜坡长度：>临界坡长； (4)岩性：泥灰岩、砂板岩、页岩、千枚岩等； (5)临空条件：前缘受阻，即坡角≤岩层倾角。

2　试验与模拟方案

2.1试验方案

2.1.1试验设备及原理

底摩擦模型试验是定性分析岩体变形破坏规律的重要方法之一。本次试验采用地质灾害防治与地质环境保护国家重点实验室设计研制的自动化底摩擦仪。优点是可根据试验情况暂停，以便观测试验过程的各个细节和现象。其以摩擦力在摩擦方向上的分布与重力场相似的性质，利用模型和底面之间的摩擦力来模拟重力。以相似原理为基础，为使试验模型的物理现象与地质原型相似，应满足相似关系(石豫川等， 2003)。

2.1.2试验模型、参数及方案

为了分析顺层斜坡溃屈机制及控制因子关系(主要为岩层倾角、单层厚度)，设计试验方案如下：

按组合共进行如下18个模型试验(图2)。

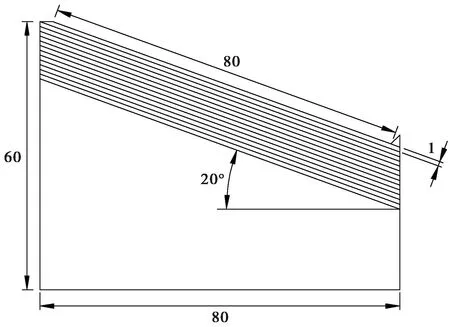
图2　模型示意图(以20°为例)(单位：cm)Fig. 2　Schematic diagram of the model(cm)

(1)岩层倾角а： 15°、20°、25°、30°、35°、40°； (2)岩层厚度h： 0.5m、1.0m、1.5m； (3)坡长L： 80m； (4)相似比C： 1︰100。

图3　不同岩层倾角和单层厚度斜坡模型试验的滑移—弯曲变形特征Fig. 3　The characteristics of buckling of bedding slope in the model test of different dip angle and layer thicknessa. H=0.5m，θ=20°； b. H=0.5m，θ=25°； c. H=0.5m，θ=30°； d. H=1.0m，θ=20°； e. H=1.0m，θ=25°； f. H=1.0m，θ=30°； g. H=1.5m，θ=20°；h. H=1.5m，θ=25°； i. H=1.5m，θ=30°

模型材料采用硫酸钡、石膏、石英砂、甘油、水、硼酸等按质量配合比拌制，通过室内试验分析得到的模型材料物理力学参数如表1所示。

表1　模型材料物理力学参数Table1　Parameters of materials

材料容重/kN·m-3泊松比μ抗压强度σc/MPa摩擦角/(°)黏聚力/MPa体积模量/GPa剪切模量/GPa岩石270.233030103.332层面///150.01//

2.2模拟方案

结合底摩擦模型试验，开展了对应的18个模型的数值分析。分析采用离散元软件UDEC，其在该领域应用广泛，是研究不连续岩体变形破坏的理想工具，可以模拟大位移、旋转、滑动、变形破坏乃至块体分离，能比较真实地模拟节理岩体中的非线性变形特征(Griffiths et al.，1999； 雷远见等， 2006)。为了对比分析，数值模型尺寸与底摩擦模型试验所代表的原型一致，参数选取相同，采用了弹塑性摩尔-库仑本构模型。

3　试验现象和模拟结果分析

图4　不同岩层倾角和单层厚度斜坡模拟分析的滑移—弯曲变形特征(单位：m)Fig. 4　The characteristics of buckling of bedding slope in numerical analysis of different dip angle and layer thicknessa. H=0.5m，θ=20°； b. H=0.5m，θ=25°； c. H=0.5m，θ=30°； d. H=1.0m，θ=20°； e. H=1.0m，θ=25°； f. H=1.0m，θ=30°； g. H=1.5m，θ=20°； h. H=1.5m，θ=25°； i. H=1.5m，θ=30°

模型试验和数值模拟效果较好，两者现象较吻合，并可以相互印证 (图3 和图4)。

3.1岩层倾角对斜坡变形破坏的影响

岩层倾角是影响和控制顺层斜坡滑移—弯曲变形的关键因素。其作用表现在如下几个方面：

(1)岩层倾角15°时，斜坡基本没有产生变形； 当岩层倾角为20°时，斜坡产生了轻微变形； 当岩层倾角为25°～40°时，斜坡岩层产生蠕动变形、且在岩层下部出现弯曲(图3、图4)。通过斜坡弯曲部位的变形监测分析 (图5)：当岩层倾角≤20°时，斜坡前缘基本稳定、没有产生隆起变形。因此认为对于层厚0.5～1.5m的顺层斜坡，当岩层倾角>20°时，才可能产生滑移—弯曲变形。这一指标是判别缓倾外顺层斜坡是否发生溃屈的重要地质条件。

图5　斜坡模型分析中隆起变形-时步曲线Fig. 5　The curve of deformation and time in the front of the slope model

图6　斜坡模型前缘临溃变形与岩层倾角关系Fig. 6　The relationship curve between the deformation and dip angle

(2)通过15°、20°、25°、30°、35°和40°等差序列岩层倾角斜坡变形破坏数值模拟分析得出：岩层倾角越大越容易产生滑移—弯曲变形，滑移—弯曲变形过程所经历的时间越短 (图5)，斜坡临溃位移量随岩层倾角的增大而增加 (图6)。

(3)当斜坡高度一定、岩层的单层厚度相同时，随着岩层倾角的增加，斜坡的溃屈层数增加，也就是随着岩层倾角的增大，斜坡的溃屈深度会随之增加(溃屈深度指前缘出现明显弯曲变形的岩层厚度，其等于弯曲变形的岩层层数×单层厚度)(图3、图4 和表2)。

表2　不同岩层倾角斜坡溃屈层数统计Table2　Statistics of buckling layer of the different dip angle slope

单层厚度/m数值分析(弯曲层数)物理模型(弯曲层数)25°30°35°40°25°30°35°40°0.5678855671.0344423341.523332333

3.2单层厚度对斜坡变形破坏的影响

不同单层厚度的斜坡模型试验和数值模拟分析结果显示 (图3、图4 和表2)：

(1)当岩层厚度为0.5m时。①岩层倾角<20°的斜坡模型试验和数值模拟均没有发生明显位移，与理论计算结果一致(理论分析结果见表3和4，图11，下同)。②岩层倾角25°时，数值模拟显示出现变形的岩层共6层，模型试验显示出现变形的岩层为5层，理论计算则为8层。③岩层倾角30°时，数值模拟结果变形岩层为7层，模型试验显示变形岩层为5层，理论计算则为9层。

表3　岩层倾角与临界坡长关系Table3　Relationship between dip angle and critical length of slope

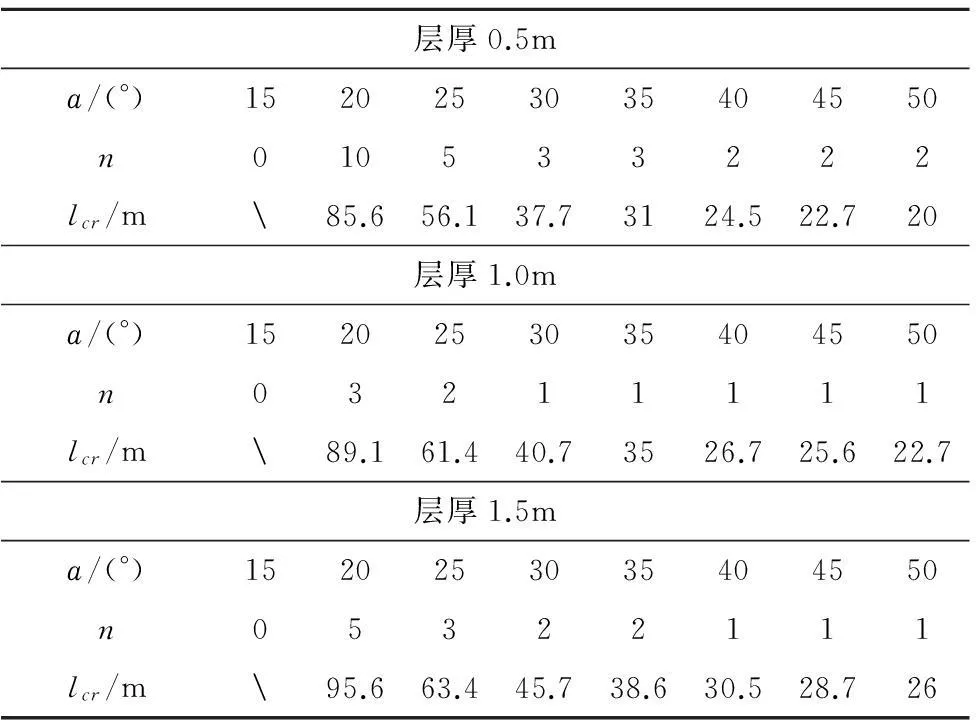
层厚0.5mа/(°)1520253035404550n010533222lcr/m85.656.137.73124.522.720层厚1.0mа/(°)1520253035404550n03211111lcr/m89.161.440.73526.725.622.7层厚1.5mа/(°)1520253035404550n05322111lcr/m95.663.445.738.630.528.726

表4　临界坡长与溃屈层数(深度)关系Table4　Relationship between buckling depth and critical length of slope

层厚0.5mа/(°)nlcr/mnlcr/mnlcr/mnlcr/m201095.611101.812107.913113.825556.1663.4770.2876.725983.01089.11194.912100.630337.7445.7553.0659.930766.4872.6978.51084.2层厚1.0mа/(°)nlcr/mnlcr/mnlcr/mnlcr/m150———————20595.66107.97119.68130.725363.4476.7589.16100.630245.7359.9472.6584.235243.6357.2469.3580.440126.5242.0355.1466.740577.4687.4796.98105.9层厚1.5mа/(°)nlcr/mnlcr/mnlcr/mnlcr/m20389.14108.05125.26141.425263.4383.04100.65116.730137.7259.9378.5495.1

(2)当岩层厚度为1m时。①岩层倾角<20°的斜坡模型试验和数值模拟均未出现明显变形，与理论计算相同。②岩层倾角25°时，数值模拟结果显示3层发生变形，模型试验结果为2层出现变形，理论计算结果为4层。③岩层倾角30°时，数值模拟结果显示4层发生变形，模型试验结果为3层出现变形，理论计算结果为4层。

(3)当岩层厚度为1.5m时。①岩层倾角<20°时，斜坡模型试验和数值模拟均未见明显位移，理论计算也是如此。②岩层倾角25°时，数值模拟和模型试验结果显示斜坡2层岩层发生了弯曲，与理论计算结果一致。③岩层倾角30°时，数值模拟和模型试验结果显示斜坡3层岩层发生弯曲，与理论计算结果一致。

(4)从材料力学角度分析，单层厚度越小、单一岩层抗弯刚度越小、越易弯曲； 且滑移—弯曲变形易于发生在单层厚度<1.5m的顺层斜坡，这一点与已有研究观点是一致的(李树森等， 1995； 任光明等， 1998； 朱玉平等， 2004； 杜应琼等， 2014)。但本文研究显示在斜坡高度和岩层倾角相同的条件下，不同层厚的顺层斜坡的溃屈深度基本相同，例如25°时的模型试验和数值模拟分析结果在3m左右，其他倾角时其溃屈深度总体来看是比较接近的(当然试验会导致产生一定误差)(表2)。分析认为当滑移部分的岩层发生弯曲时，由于层间黏结作用而具有共同抗弯的效应(在此称之为“共弯效应”)。因此单层厚度对产生滑移—弯曲变形的那部分岩层整体抗弯刚度影响不大，而溃屈深度(弯曲层数×层厚)对斜坡滑移—弯曲岩层整体抗弯刚度及最终溃屈状态起决定性作用。这一认识对于该类斜坡灾害防治具有重要的参考价值。

3.3顺层斜坡滑移—弯曲变形破坏过程

通过地质、物理模型试验和数值模拟分析与归纳，认为顺层斜坡溃屈经历了如下几个阶段 (图7)：

图7　顺层斜坡滑移—弯曲变形破坏过程Fig. 7　The failure process of creep-buckling of the bedding slope

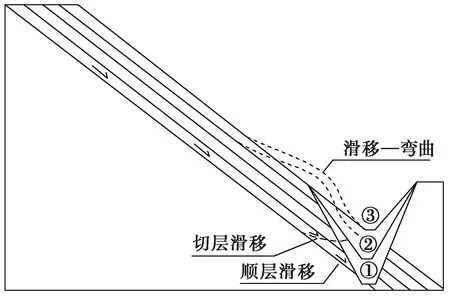
图8　不同临空条件下的顺层斜坡变形Fig. 8　Bedding slope in different free-face conditions

(1)顺层蠕滑阶段 (图7a)。当上覆岩层克服层间摩阻力而出现剩余下滑力时，上覆岩层才开始向下蠕滑，继而产生层间错动和坡顶下沉现象。

(2)前缘隆起弯曲阶段 (图7b)。随着坡脚应力集中程度的加大，岩层开始出现弯曲变形，斜坡前缘坡面开始隆起。基于岩石蠕变力学理论分析认为在这种斜坡应力环境条件下此时的斜坡最终发生溃屈已不可避免。因此斜坡坡脚岩层出现弯曲变形这一关键状态可以作为顺层斜坡溃屈破坏早期识别的重要标志。

(3)强烈弯曲—破坏(溃屈)阶段 (图7c)。当岩层弹性弯曲变形达到一定程度时，岩层会出现塑性变形、折断或错断，进而逐层发展至最终破坏。

4　溃屈条件及关键因子作用分析

4.1溃屈产生条件

对于不同临空条件的顺层斜坡，可能发生顺层滑移、切层滑移或滑移—弯曲(图8)。当岩体沿着软弱面有滑动趋势时，在图8-①的临空条件下，临空面完全切穿滑体软弱面，滑体会沿软弱面自由滑出； 在图8-②的临空条件下，虽然滑体的变形受到一定限制，但滑体有可能剪断坡脚处岩体而发生切层滑动； 在图8-③的临空条件下滑体前缘受阻无自由滑出的空间，在剩余下滑力的作用下可能发生滑移弯曲—变形破坏。在此主要讨论第③种情况。

软弱岩体具有蠕变特性(杨天鸿等， 2003)，在上覆岩层剩余下滑力作用下，一旦坡脚岩层出现了“弹性弯曲变形”，在其斜坡应力环境条件下，随着蠕变发展，最终发生溃屈是不可避免的。据此推导其力学条件如下：

所建立力学模型(图9)，斜坡长度为l，滑移段长度为l1，弯曲岩体长度为l2，岩层层数为n，单层厚度为h，岩层倾角为α。岩体容重为γ，弹性模量为E，层间内摩擦角为φ，黏聚力为c，则有：

图9　顺层斜坡滑移—弯曲力学模型Fig. 9　Mechanics model of buckling of bedding slope

(1)首先斜坡发生滑移—弯曲变形的前提条件是存在剩余下滑力，分析可得下滑力：

(1)

(2)岩层弹性弯曲的临界下滑力Fcr，根据压杆稳定的欧拉公式计算可得：

(2)

(3)综上可知，斜坡岩层发生滑移—弯曲变形时应满足F≥Fcr，即：

(3)

若同时满足上述条件，理论上则可以判断斜坡会发生滑移—弯曲变形。在此需要注意，斜坡切向应力影响因素较多，其值尚难以采用公式定量表述，如果存在较大切向分力则临界坡长比这一公式计算稍小。

4.2关键致灾因子相互作用关系

在机制分析和理论计算的基础上，在此进一步分析影响因子相互关系。以物理模型试验和数值模拟代表的斜坡为例，采用上述理论可以计算分析临界坡长、岩层倾角、溃屈深度(或岩层层数)等。

如果斜坡岩层倾角为30°，将表1中模型材料及层面力学参数代入式(1)，可得剩余下滑力：

F=(7.23nh-10)l1

(4)

对于二维模型，参考孙广忠(1988)推导的理论公式计算临界坡长：

(5)

4.2.1临界坡长、岩层倾角和层厚关系

根据式(4)和(5)计算分析岩层倾角30°时的溃屈变形层数与斜坡临界坡长。同理可分析计算其他岩层倾角和层厚的斜坡(表3和图10)。

图10　斜坡岩层倾角与临界坡长关系Fig. 10　Relationship curve between dip angle and critical length of slope

分析显示 (表3 和图10)：随着岩层倾角的增加，斜坡溃屈的临界坡长呈现负幂函数变化，与临界坡长理论公式表达一致。同一岩层倾角下，层厚较小的所需斜坡临界坡长相对较小，但是影响不大。相对来说，溃屈深度才是真正影响斜坡弯曲部分整体抗弯刚度的主要因素，进而影响到斜坡溃屈的临界坡长，因此影响斜坡临界坡长的主要因素是岩层溃屈深度。据此分析认为当斜坡高度和岩层倾角相同的条件下，不同层厚的顺层斜坡的溃屈深度和临界坡长基本一致。

4.2.2临界坡长与溃屈破坏深度关系

同理分析可得其相互关系见表4和图11。

图11　不同层厚时溃屈深度与临界坡长关系Fig. 11　Relationship between buckling depth and critical length of slopea. 层厚0.5m， b. 层厚1.0m， c. 层厚1.5m

在坡长相同的情况下，随着岩层倾角的增加，斜坡岩层溃屈层数(溃屈深度)增大。在溃屈深度相同的情况下，岩层倾角越大，产生初始溃屈破坏的所需临界坡长越小，即越容易产生溃屈破坏。工程实践中，当斜坡岩层中存在软弱面时，且岩体沿软弱面具有向下滑移趋势，那么岩层(软弱面)倾角越大，斜坡溃屈的临界坡长越小，越容易发生溃屈破坏。

5　结　论

本文采用物理机制模型、数值模拟和理论计算相结合的方法，克服了单一分析方法的局限性，从不同角度层次较为系统地分析研究了顺层斜坡滑移—弯曲(溃屈)变形破坏过程和机理，研究探讨了其关键致灾因子关系及早期识别指标，得出了如下结论和认识：

(1)顺层斜坡滑移—弯曲(溃屈)变形破坏过程可分为顺层—蠕滑→前缘隆起—弯曲→强烈弯曲—破坏3个阶段。当斜坡演化进入第二阶段后，在其斜坡应力环境条件下最终发生溃屈将不可避免，前缘隆起弯曲可以作为顺层斜坡临溃状态早期识别的重要标志。

(2)岩层倾角是影响和控制顺层斜坡滑移—弯曲变形的关键因素。岩层倾角越大越容易产生滑移—弯曲变形； 随着岩层倾角的增加，斜坡岩层溃屈层数(溃屈深度)增大。岩层倾角>20°是判别缓倾外顺层斜坡是否会发生溃屈变形的重要地质条件。

(3)单层厚度越小、单一岩层的抗弯刚度越小，越易弯曲，这一点是共识。但是本文研究认为由于层间黏结作用而具有共同抗弯的效应(在此称之为“共弯效应”)，在斜坡高度和岩层倾角相同的条件下，单层厚度对产生滑移—弯曲变形的那部分岩层整体抗弯刚度影响不大，而溃屈深度(弯曲层数×层厚)对斜坡滑移—弯曲岩层整体抗弯刚度及最终溃屈状态起决定性作用。

(4)斜坡溃屈临界坡长随着岩层倾角的增加而减小，呈现负幂函数变化趋势。岩层倾角相同时，单层厚度小的所需临界坡长也小，但是单层厚度对临界坡长的影响不大，其主要影响因素是岩层溃屈深度。当斜坡高度和岩层倾角相同的条件下，不同层厚的顺层斜坡的溃屈深度和临界坡长基本一致。

(5)在坡长相同的情况下，斜坡溃屈层数(溃屈深度)随着岩层倾角的增大而增加。溃屈深度相同的情况下，岩层倾角越大，越容易产生溃屈破坏。

(6)顺层斜坡溃屈的早期识别包括地质条件和力学条件分析识别。地质条件为中软岩顺层斜坡，存在软弱夹层，层厚不大于2.0m、岩层倾角20°～50°且不小于斜坡坡度。力学条件可通过理论分析推导的滑移—弯曲变形的力学判据进行分析。

(7)对于岩性(弹性模量)和滑移面力学强度的影响还有待进一步研究。一般来说主要发生于泥灰岩、砂板岩、千枚岩、页岩等中软岩，潜在滑移面指存在软弱夹层。

Du Y Q，Ren G M，Du F，et al. 2014. Physical simulation of consequent slope bulking deformation and its influencing factor sensitivity analysis[J]. Journal of Sichuan University of Science & Engineering(Natural Science Edition)，27(6)： 68～71．

Feng J，Zhou D P，Yang T. 2010. Stability analysis of consequent rock slopes using elastic-plastic plate theory[J]. Chinese Journal of Geotechnical Engineering，32(8)： 1184～1188．

Griffiths D V，Lane P A. 1999. Slope stability analysis by finite elements[J]. Geotehnique，49(3)： 387～403．

Huang R Q，Zhao J J，Ju N P，et al. 2007. Study on deformation mechanism and control method of bedding rock slope along tangtun expressway[J]. Chinese Journal of Rock Mechanics and Engineering，26(2)： 239～246．

Jiang L W，Huang R Q. 2006. Studies on estimate of sliding-bending rupture of bedded rock slopes[J]. Journal of Mountain Science，24(1)： 88～94．

Lei Y J，Wang S L. 2006. Stability analysis of jointed rock slope by strength reduction method based on UDEC[J]. Rock and Soil Mechanics，27(10)： 1693～1698．

Li Q，Zhang Z Y. 1990. Mechanism of buckling and creep-buckling failure of the bedding rockmass on the consequent slope[A]. Proc of the 6th International Congress of IAEG[C]. Rotterdam： A A Balkema， 257～260．

Li S S，Ren G M，Zuo S S. 1995. Mechanical analysis of instability mechanism of consequent slope in bedded rockmass[J]. Journal of Geological Hazards and Environment Preservation，6(2)： 24～29．

Liu J. 1997. Mechanical analysis of bend failure of anaclinal slope[J]. Journal of Engineering Geology，5(4)： 335～339，356．

Liu X L，Zhou D P. 2002. Stability analysis of layered dip rocky slopes with elastic plane theory[J]. Rock and Soil Mechanics，23(2)： 162～165．

Ren G M，Li S S，Nie D X，et al. 1998. The physical simulation and mechanical analysis on landslide’s formation mechanism on consequent slope[J]. Mountain Research，16(3)： 182～187．

Shi Y C，Feng W K，Feng X G，et al. 2003. Study on mechanism of deformation failure of a low-angle dip bedding slope of national highway No.108 by physical simulation method[J]. Journal of Chengdu University of Technology(Science & Technology Edition)，30(4)： 350～355．

Sun G Z. 1988. Mechanics of rock mass structures[M]. Beijing： Science Press．

Wang Z Y. 1998. Research on displacement criterion of structural deformation and failure for bedding rock slope[J]. Scientia Geological Sinica，7(2)： 217～224．

Wei Y F，Nie D X，Lü S D，et al. 2009. The mechanism analysis of sliding-bending destruction mode of consequent bedded slope in the alternatively distributed soft and hard rock layers[J]. Journal of Chengdu University of Technology(Science & Technology Edition)，36(3)： 287～291．

Yan M，Chen J P，Huang R Q，et al. 2005. Engineering geological analysis on intermediate state before slide-bending failure for rock slope[J]. Water Resources and Hydropower Engineering，36(11)： 41～44．

Yang T H，Rui Y Q，Li L C，et al. 2003. Study on deformation mechanism and dynamic stability of bedding creeping slope[J]. Journal of Engineering Geology，11(2)： 155～161．

Zhu Y P，Mo H H. 2004. On critical length of flexural slumping rock layer in layered rocky slope and its influencing factors[J]. Rock and Soil Mechanics，25(2)： 283～286．

杜应琼，任光明，杜飞，等. 2014. 顺层斜坡溃屈变形物理模拟及影响因素敏感性分析[J]. 四川理工学院学报(自然科学版)，27(6)： 68～71．

冯君，周德培，杨涛. 2010. 用弹塑性板理论分析顺层边坡的弯曲失稳[J]. 岩土工程学报，32(8)： 1184～1188．

黄润秋，赵建军，巨能攀，等. 2007. 汤屯高速公路顺层岩质边坡变形机制分析及治理对策研究[J]. 岩石力学与工程学报，26(2)： 239～246．

蒋良潍，黄润秋. 2006. 层状结构岩体顺层斜坡滑移—弯曲失稳计算探讨[J]. 山地研究，24(1)： 88～94．

雷远见，王水林. 2006. 基于离散元的强度折减法分析岩质边坡稳定性[J]. 岩土力学，27(10)： 1693～1698．

李树森，任光明，左三胜. 1995. 层状结构岩体顺层斜坡失稳机理的力学分析[J]. 地质灾害与环境保护，6(2)： 24～29．

刘钧. 1997. 顺层边坡弯曲破坏的力学分析[J]. 工程地质学报，5(4)： 335～339，356．

刘小丽，周德培. 2002. 用弹性板理论分析顺层岩质边坡的失稳[J]. 岩土力学，23(2)： 162～165．

任光明，李树森，聂德新，等. 1998. 顺层坡滑坡形成机制的物理模拟及力学分析[J]. 山地研究，16(3)： 182～187．

石豫川，冯文凯，冯学钢，等. 2003. 国道108线某段缓倾角顺层边坡变形破坏机制物理模拟研究[J]. 成都理工大学学报(自然科学版)，30(4)： 350～355．

孙广忠. 1988. 岩体结构力学[M]. 北京：科学出版社．

魏玉峰，聂德新，吕生弟，等. 2009. 溃曲软硬相间顺层斜坡滑移—弯曲破坏机制分析[J]. 成都理工大学学报(自然科学版)，36(3)： 287～291．

严明，陈剑平，黄润秋，等. 2005. 岩质边坡滑移—弯曲破坏中间状态的工程地质分析[J]. 水利水电技术，36(11)： 41～44．

杨天鸿，芮勇勤，李连崇，等. 2003. 顺层蠕动边坡变形破坏机理及稳定性动态分析[J]. 工程地质学报，11(2)： 155～161．

朱玉平，莫海鸿. 2004. 顺倾边坡岩层滑移弯曲临界长度及其影响因素分析[J]. 岩土力学，25(2)： 283～286．

EARLY RECOGNITION AND MECHANISM OF CREEP-BUCKLING OF BEDDING SLOPE

TANG Minggao①MA Xu①ZHANG Tingting①HUANG Runqiu①LI Jiuqian②

(①State Key Laboratory of Geohazard Prevention and Geoenvironment Protection(Chengdu University of Technology)，Chengdu610059)(②Institute of Survey and Design of Sichuan Jiaotong， Chengdu610017)

This paper analyzes the mechanism of buckling failure(slipping-bending) of the bedding slope. It uses physical mechanism model， numerical simulation and theoretical analysis. It presents the forming geological and mechanical conditions， the critical failure state discrimination and early identification marks of buckling failure. It finds that the rock stratum dip angle greater than 20°is a very important geological conditions for the formation of slipping-bending. The curved uplift in the leading edge of the slope is an early sign before buckling failure. The dip angle of rock slope， the single layer thickness， the critical slope length and the depth of the buckling interact each other. The larger the rock dip angle， the more prone to produce the slipping and bending， and the more the number of layer and depth of buckling. There is a change law of negative power function between the critical slope length and the rock stratum dip angle. The flexural rigidity of bending layer and the buckling depth of bedding slope are influenced by the co-bending effect produced by the interlayer bonding. The co-bending effect plays a key role on the ultimate buckling of the bedding slope. The results have an important value for early prevention and recognition of geological hazard．

Geological hazard， Bedding slope， Creep-buckling failure， Early recognition， Experiment of bottom friction， Numerical simulation

10.13544/j.cnki.jeg.2016.03.014

2015-09-09;

2016-01-17.

973计划项目(2013CB733202)，国电猴子岩水电科研专题，中国电建集团科技项目(AQ2013-01-01)资助.

汤明高(1978-)，男，博士，副教授，主要从事工程地质与岩土工程教学科研. Email: tomyr2008@163.com

P642.22

A