一种基于模式匹配法的窄带Iris波导滤波器设计*
陈昌明,黄 刚,刘 勇
(成都信息工程大学通信工程学院,成都610225)
一种基于模式匹配法的窄带Iris波导滤波器设计*
陈昌明*,黄刚,刘勇
(成都信息工程大学通信工程学院,成都610225)
提出了一种基于模式匹配法的窄带Iris波导滤波器设计方法,通过引入Matlab优化使滤波器设计周期缩短了约1/3。设计的窄带滤波器相对带宽小于3%,且较好的克服了毫米波频段滤波器高频端带外抑制较差的难题。测试结果表明,该带通滤波器插入损耗小于0.8 dB,驻波比小于1.2,中心频率34.86 GHz,带外抑制52 dB@36.5 GHz,已被成功应用于某毫米波雷达通信系统中。
模式匹配;Iris波导;MATLAB;窄带;毫米波
波导滤波器具有通带区域内对信号呈现匹配传输,阻带区域内对信号呈现失配衰减特性,能够实现选频、分频和隔离等多种功能,是毫米波通信系统中重要组件,其性能好坏对整个通信系统有着至关重要的作用。Iris波导滤波器具有插入损耗低、功率容量大、Q值高[1-2],体积小以及加工方便等优点,已经广泛引用于毫米波通信、射电天文、雷达制导和电磁对抗等领域。目前设计这类滤波器方法主要有传统等效电路法以及采用基于有限元法的高频仿真软件 HFSS(High Frequency Simulation Software)设计,但是等效电路法由于忽略了高次模和膜片厚度的影响使设计的滤波器精度受限[3],并且调试难度和器件一致性都很难保证,而HFSS软件设计的缺点是优化、求解过程缓慢,耗费时间较多。模式匹配法是一种属于半解析半数值的求解方法[4-5],采用横向电磁场匹配方式来求解不连续面两侧模式数之间的关系,并最终导出不连续面的S参数矩阵,其优势在于考虑了金属膜片厚度和不连续处高次模的影响,其截断误差小、解析精度高。基于此,本文采用模式匹配法设计了一种用于毫米波通信系统的窄带Iris波导滤波器,并且编写了相应的Matlab优化代码,通过HFSS软件提取相应的耦合系数和外部Qe值,并最终将滤波器模型导入到HFSS中验证了设计的正确性。
1 Iris波导滤波器分析
矩形波导滤波器是截面为矩形的空心金属腔,其两个物理尺寸a和b分别代表内腔体的宽边和窄边长度,由于具有封闭结构,能够有效的屏蔽外界干扰和辐射,减小导体损耗。Iris波导加工图如图1所示,其中w为耦合腔宽,t为耦合腔长,L0为谐振腔长度,由于加工过程中外直角加工难度大,所以在外直角处倒半径为R的圆弧。模式匹配法的基本思路是根据不连续面分界处的电场和磁场切向分量分别相等,通过匹配横向电场,求解出波导的不连续性散射矩阵,图1中I区和II区不连续面处散射矩阵数学表达式为[6-7]:
项目来源:四川省教育厅重点项目(13ZA0087)
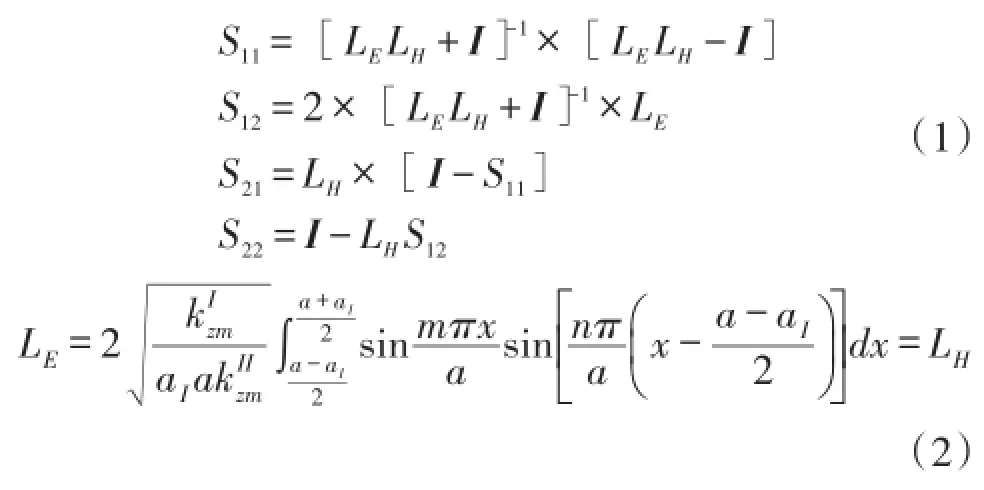
式中,I为单位矩阵,LE、LH分别为不连续面处切向电场和磁场分量,m、n为模式数,为图1中I区传播模式为图1中II区传播模式。
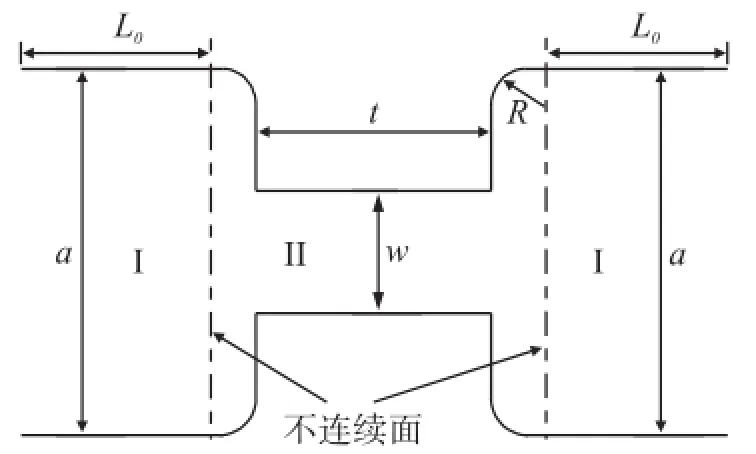
图1 Iris波导加工图
根据等波纹切比雪夫滤波器低通原型,由滤波器设计指标要求可以计算出滤波器阶数N和相应的归一化元件参数值为:g0,g1,g2,…,gN+1,由此可以得出串联谐振腔拓扑结构耦合矩阵为[8]:

其中Mj,j+1表示相邻谐振腔间归一化耦合元件值,且有Mi,j=Mj,i。
由公式(3)的拓扑结构耦合矩阵可知,对于对称耦合谐振腔的情况,两个谐振腔谐振频率完全相同,这样可以将耦合谐振腔从对称面劈开,其结构如图2所示。在对称面上分别设置为完全导电面(PEW)和完全导磁面(PMW),在HFSS中利用本征模求解器,得到相应的本征频率分别为fe和fm,耦合系数k可以用下面的公式计算得到[9-10]:

其中,k为正表示磁耦合,k为负表示电耦合。

图2 耦合谐振腔
如果两个谐振腔是非对称的,同样可以采用上述方法,将两谐振器从中间劈开,每一个谐振器在对称面上分别设置完全导电面和完全导磁面,这时将得到4个本征频率分别为fe1、fm1、fe2和fm2这样,非对称耦合结构的耦合系数k为:

其中,k为正表示磁耦合,k为负表示电耦合。
2 设计实例
结合工程实际需求,文中设计的窄带毫米波波导滤波器用于某型毫米波雷达通信系统中,其主要设计指标如下:中心频率:34.86 GHz相对带宽:≤3%;带外抑制:≥50 dB@36.5 GHz;带内插损:≤0.8 dB;驻波比:≤1.2。根据设计指标要求,选择5阶切比雪夫(Chebyshev)滤波器低通原型,波导选择 BJ320 (7.12 mm×3.56 mm),由式(3)综合出耦合矩阵为:

根据综合出的耦合矩阵分析可知,滤波器为对称性无源器件,在S参数里面表现为S11=S22,且5阶低通原型综合得到了一个7×7阶耦合矩阵,主要是因为添加了分别代表源和负载的耦合系数项的,转换为几何参数即为外部Qe值,其表达式为:
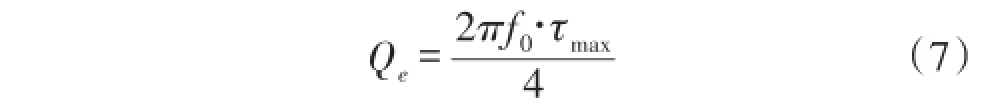
其中,τmax为输入端反射系数S11对应值的最大群时延值,f0为滤波器中心频率,在此处即为34.86 GHz,由此可以计算出Qe=29.03。文中设计的滤波器耦合谐振腔为对称结构,所以根据公式(6)计算出的耦合矩阵参数并利用公式(4)可以推导出滤波器各阶耦合系数分别为:kS,1=0.028=k5,L、k1,2=0.025=k4,5、k2,3= 0.017=k3,4,然后利用HFSS本振模求解器,通过建立两个对称排列的耦合腔谐振器模型,改变耦合腔宽度w和谐振腔长度L0,可以观察到耦合系数的变化情况。图3为耦合系数k随耦合腔宽度w变化情况的扫描曲线,由曲线可知当k=0.017 0和k=0.028 5时,w=2.75 mm和w=2.60 mm,采用同样方法可以求出滤波器剩下几阶腔体的物理尺寸,滤波器初始尺寸如表1所示,至此,已经计算出设计滤波器所需的全部几何尺寸。
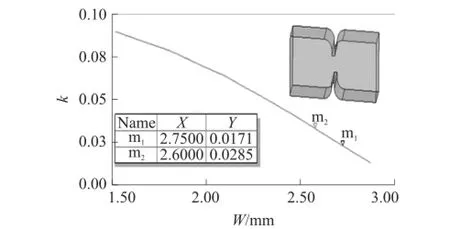
图3 耦合系数k与w的关系曲线
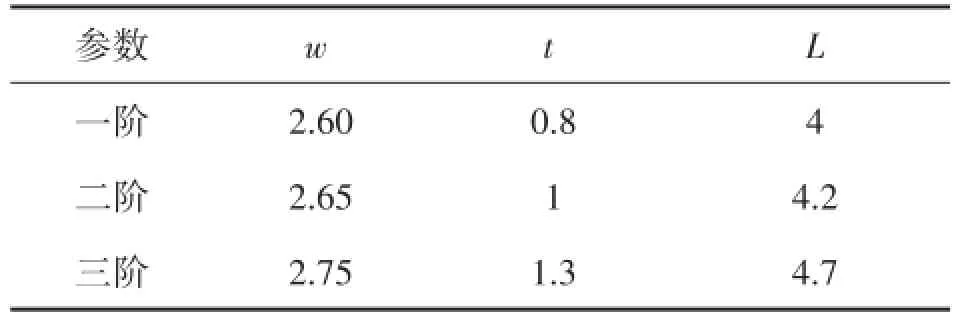
表1 滤波器几何尺寸初始值 单位:mm
2.1基于模式匹配法的Matlab滤波器优化
传统设计方法中,在计算出滤波器几何尺寸初始值后,一般采用HFSS软件对系统模型的物理尺寸进行优化,由于HFSS采用的是基于有限元法的网格剖分技术[11-13],虽然能够求解任意结构的物理模型,但是在计算时间和资源占用方面消耗较多,从而降低了产品的设计效率和周期。为此,本文采用基于模式匹配法的Matlab编程对滤波器进行优化,充分利用Matlab强大而高效的数值计算能力,简化繁杂的数学运算分析特点并结合模式匹配法分析几何结构时间精度高、运算速度快等优势,设计了可用于优化波导滤波器性能的相应程序和算法,与传统设计方法相比,采用本文提出的设计思路可以使滤波器设计周期缩短约1/3,其相应的部分核心算法代码如下所示。
%根据公式(1)求解不连续面处广义散射矩阵S参数
S11(:,:,p)=(inv(L_Emn(:,:,p)*L_Hmn(:,:,p)+eye (q,q)))
*(L_Emn(:,:,p)*L_Hmn(:,:,p)-eye(q,q));
S12(:,:,p)=2*(inv(L_Emn(:,:,p)*L_Hmn(:,:,p)+ eye(q,q)))
*L_Emn(:,:,p);
S21(:,:,p)=L_Hmn(:,:,p)*(eye(q,q)-S11(:,:,p));
S22(:,:,p)=eye(q,q)-L_Hmn(:,:,p)*S12(:,:,p);
%耦合谐振腔几何尺寸的优化求解
w=2*pi*((p-1)*(4e10-3e10)/100+3e10);
K_zm((m+1)/2,p)=conj(sqrt(w^2*mu*epsilon-(m*pi/a)^ 2));
K_zn((n+1)/2,p)=conj(sqrt(w^2*mu*epsilon-(n*pi/W)^ 2));
t_E(:,:,p)=diag(exp(-j*K_zm(1:q,p)*x));
t_H(:,:,p)=diag(exp(-j*K_zn(1:q,p)*x));
%不连续面处切向电场和磁场分量求解
L_Emn((m+1)/2,(n+1)/2,p)=2*sqrt(K_zm((m+1)/2,p)/(a*W*K_zn((n+1)/2,p)))*x;
L_Hmn((n+1)/2,(m+1)/2,p)=L_Emn((m+1)/2,(n+1)/ 2,p);
将Matlab优化得到的滤波器模型导入到HFSS中进行验证,其仿真结果如图4所示,滤波器最终优化尺寸值如表2所示。由图可知,滤波器带内损耗0.5 dB,带外抑制54.3 dB@36.5 GHz,中心频率34.86 GHz。
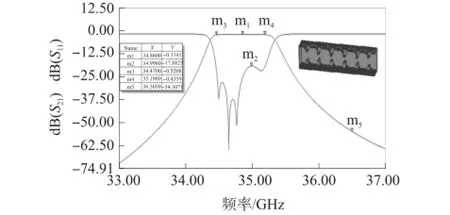
图4 HFSS滤波器仿真结果

表2 滤波器优化后几何尺寸值 单位:mm
2.2滤波器关键参数的扫描与分析
为了获取滤波器性能与具体某些参数的相关性,为今后的设计起到指导作用,文中给出了其中一些关键参数的变化对滤波器性能的影响,如图5~图7所示。
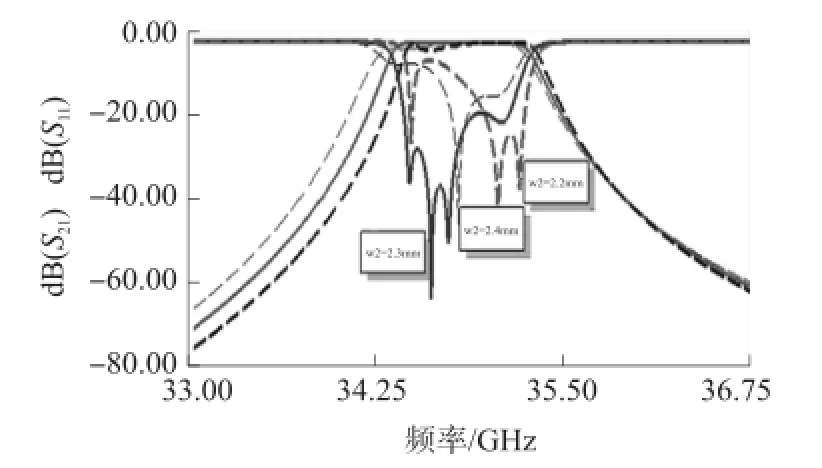
图5 w2对滤波器性能影响
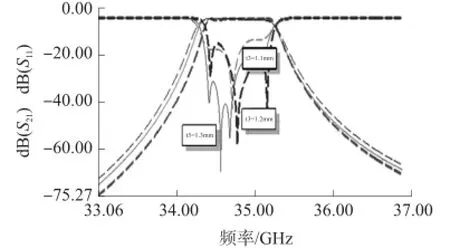
图6 t3对滤波器性能影响
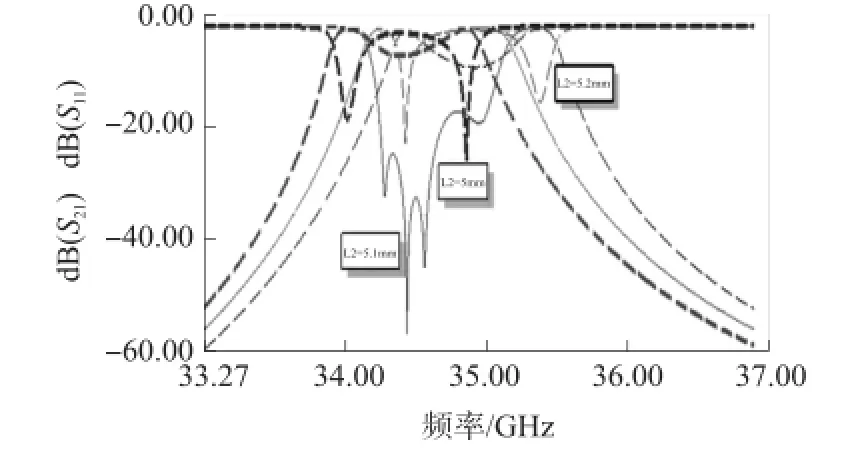
图7 L2对滤波器性能影响
由以上扫描结果分析可知,滤波器参数S11与耦合腔宽度w和长度t相关性较大,而耦合腔长度w起主要作用,谐振腔长度L决定了滤波器谐振频率和S21性能,外倒角R对滤波器中心频率也有一定影响。
3 测试结果与分析
滤波器制作实物如图8所示,整个模型尺寸为35 mm×9.12 mm×5.56 mm,采用安捷伦N5244A矢量网络分析仪进行测试,最后得到测试结果与Matlab仿真结果对比图如图9所示。

图8 Iris波导滤波器实物图
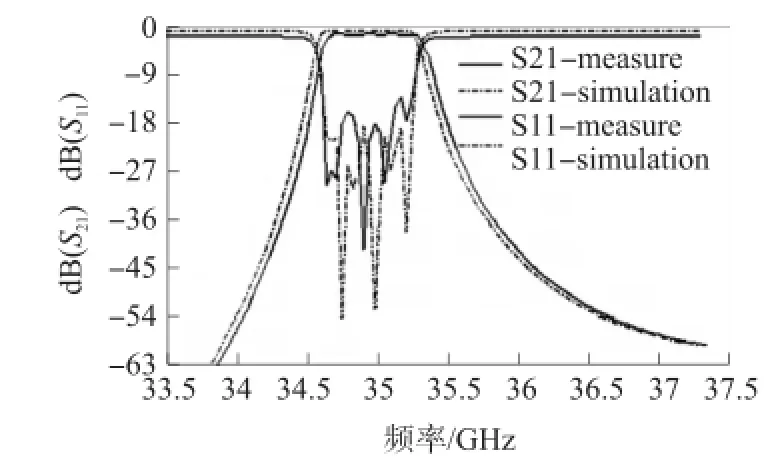
图9 测试结果与Matlab仿真结果图
由图9可知,测试结果和仿真结果符合较好,没有出现中心频率偏移,通带内滤波器损耗小于0.8 dB,相对带宽小于3%,带外抑制52 dB@36.5 GHz,较好的满足了设计指标要求。
4 结束语
同传统设计方法相比,本文提出了一种基于模式匹配法的窄带波导滤波器设计方法,并通过Matlab优化大大缩短了滤波器设计周期。文中从滤波器的理论分析到转化为计算机辅助(CAD)软件设计,并最终制作出实物测试一系列过程验证了该方法的可行性和正确性。设计的Iris波导滤波器难点在于相对带宽低于工程设计经验认为的15%窄带标准,并且很好的克服了毫米波频段滤波器高频端带外抑制较差的难题和中心频率偏移问题,对其它窄带滤波器的设计起到了一定的指导作用和借鉴意义。
[1] 李欣,禹旭敏,李燕.一种大功率宽带毫米波波导滤波器[J].微波学报,2012,28(S2):218-220.
[2] Firas Sammoura,Lin Liwei.Micromachined W-Band Polymeric Tunable Iris Filter[J].Microsystem Technologies,2011,17(3):411-416.
[3Miguel Angel Tlaxcalteco-Matus.Modeling a SIW Filter with IRIS Windows Using Equivalent Circuits[J].Microwave and Optical Technology Letters,2012,54(12):2865-2868.
[4] Luke Murphy.Design of a Dielectric Waveguide Filter with Embedded Metamaterial Using Mode Matching Technique[J].Microwave and Optical Technology Letters,2014,56(2):443-446.
[5] Shang Xiaobang,Lancaster Michael J.Microwave Waveguide Filter with Broadside Wall Slots[J].Electronics Letters,2015,51 (5):401-403.
[6] 陆彬,周邦华,吕立明.带倒角的波导H面阶梯滤波器分析及设计[J].信息与电子工程,2011,9(6):718-721.
[7] 黄近秋,曹建忠,王善进.一种简单微带线/共面波导结构的新型超宽带带通滤波器[J].电子器件,2013,36(6):806-809.
[8] 王文才,陈昌明,杨刚.一种毫米波微带带通滤波器的设计[J].电子器件,2014,37(5):855-858.
[9] Hong Jiasheng.Couplings of Asynchronously Tuned Coupled Microwave Resonators[J].IEEE Microwaves Antennas and Propagation,2000,147(5):354-358.
[10]李荣强,杜国宏,唐军.过模基片集成波导腔体滤波器设计[J].微波学报,2014,30(3):93-96.
[11]刘类骥.小型化窄边单脊波导滤波器设计[J].压电与声光,2013,35(6):903-906.
[12]谢绰,杨维明,杨武韬,等.小型化超宽阻带共面波导低通滤波器设计[J].电子器件,2014,37(5):867-870.
[13]马敏,黄健,喻志远,等.E面金属膜片波导滤波器的优化设计[J].电讯技术,2003,43(1):73-76.

陈昌明(1971-),男,汉族,四川安县人,教授,硕士生导师,主要研究方向为射频、微波/毫米波电路与系统;

黄刚(1989-),男,汉族,四川资阳人,硕士研究生,主要研究方向为微波/毫米波电路与系统,326052253@qq.com;

刘勇(1992-),男,汉族,河南周口人,硕士研究生,主要研究生方向:微波/毫米波电路与系统。
Design of a Narrow-Band Iris Waveguide Filter Based on Mode-Matching Method*
CHEN Changming*,HUANG Gang,LIU Yong
(College of Communication Engineering Chengdu University of Information Technology,Chengdu 610225,China)
A design method of narrow-band Iris waveguide filter based on Mode-matching is proposed.This design cycle of the filter is shortened a third by the help of Matlab optimization.The relative bandwidth of narrow-band filter is less than 3%.This filter overcomes the problem that high frequency out of band suppression is poor in the millimeter-wave band.The test results show that the insertion loss of the filter is less than 0.8 dB,voltage standingwave ratio(VSWR)is better than 1.2,center frequency is 34.86 GHz,the out-of-band rejection is 52 dB at 36.5 GHz and it has been successfully used in a millimeter wave radar communication system.
mode-matching;Iris waveguide;MATLAB;narrow-band;millimeter-wave
TN713
A
1005-9490(2016)03-0517-05
EEACC:135010.3969/j.issn.1005-9490.2016.03.004
2015-07-22修改日期:2015-10-16

