基于ΔVGS高阶温度补偿的高精度CMOS带隙基准源*
陈培腾,王卫东,黎官华
(桂林电子科技大学信息与通信学院,广西桂林541004)
基于ΔVGS高阶温度补偿的高精度CMOS带隙基准源*
陈培腾,王卫东*,黎官华
(桂林电子科技大学信息与通信学院,广西桂林541004)
利用两个工作在亚阈区的MOS管的栅源电压差ΔVGS产生高阶补偿量,对传统的BJT带隙基准源进行高阶温度补偿。设计一种基于ΔVGS高阶温度补偿的高精度CMOS带隙基准。电路基于CSMC 0.5 μm标准CMOS工艺设计,仿真结果表明:在5 V电源电压下,基准输出电压为1.258 V;在-40℃~125℃的温度范围内,温度系数为1.24×10-6/℃;低频时电源抑制比PSRR为-68 dB;电源电压在3.5 V~6.5 V范围内工作,线性调整率为0.4 mV/V。适用于高精度带隙基准源。
带隙基准(BGR,Bandgap Reference);亚阈区;低温度系数
随着集成电路工艺的发展和电源电压的降低,基准电压源是模拟和混合信号集成电路的重要基本单元模块,在电路系统中能够提供高精度的基准电压,被广泛应用于DAC、ADC、DC-DC、振荡器等电路中。带隙基准源的精度,在某种程度上直接影响到芯片,甚至整个电路系统的性能。因此,设计一个高精度的基准源具有十分重要的意义[1]。
传统的带隙基准源已经不能满足高精度系统的需求,为了提高CMOS带隙基准电压源的精度,人们提出了很多种补偿技术。Rincon-Mora和Allen提出了分段线性方法取消VBE的非线性温度特性;Ka Nang Leung等提出通过不同类型的工艺电阻进行非线性高阶补偿;Andreou[2]提出两种温度系数相反的电流来实现高阶补偿。本文利用两个工作在亚阈区的MOS管的栅源电压差ΔVGS相对于传统的带隙基准源具有相反的高阶温度系数,设计了一种高精度的CMOS带隙基准源。
1 传统的带隙基准源(BJT BGR)
对于一个双极型晶体管,其集电极电流IC与基极-发射极电压VBE的关系为:
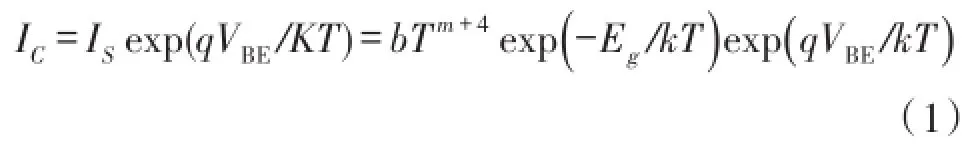
其中,IS为双极型晶体管的饱和电流;VT是热电压;Eg为Si的带隙能量;m为电子迁移率的温度指数;b为常数。根据式(1)可以得到VBE的温度系数为:

收稿日期:2015-07-25修改日期:2015-09-07
根据经验值,当 VBE≈750 mV,T=300 K时,∂VBE/∂T=-1.5 mV/°C。则VBE具有负的温度系数。
如果两个双极型晶体管工作在不相等的电流密度下,那么他们的基极-发射极电压之差ΔVBE就与绝对温度成正比。假设两个相同的晶体管(IS1=IS2),集电极电流分别为NI0和I0,其中N是晶体管Q2和Q1的发射极面积比。忽略他们的基极电流,那么:
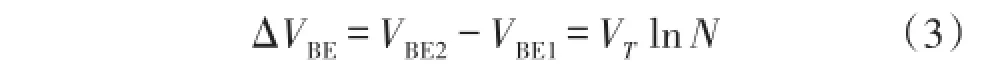
所以ΔVBE为正的温度系数。
带隙基准源的工作原理是利用两种具有相反温度系数的量以适当的权重相加后,得到一个零温度系数的输出电压。传统的带隙基准源如图1所示,其基于VBE和ΔVBE具有相反的温度系数,用ΔVBE正的温度系数补偿VBE负的温度系数,从而得到具有较低温度系数的输出电压[3]。

图1 传统的带隙基准源
其中M1、M2和运放构成一个负反馈,使得X和Y点的电位相等。M1、M2和M3构成电流镜,假如M1、M2、M3的宽长比相等,那么各电流为
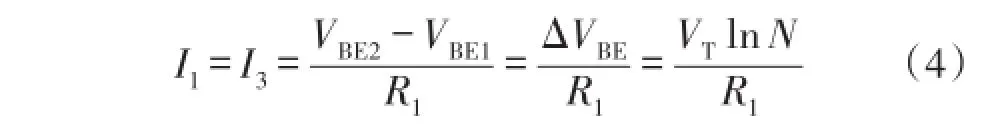
那么输出电压为:
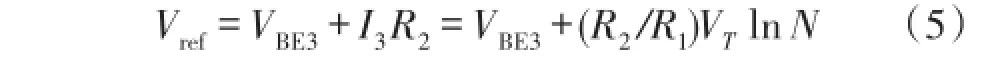
由式(5)可知,只要选取适当的R1、R2和N的值即可得到与温度无关的Vref。
2 基于MOS亚阈值特性的基准源(MOS BGR)
基于MOS亚阈值特性的带隙基准源如图2所示[4]。工作在亚阈区的NMOS管的亚阈值电流ID可表示为:

其中VGS是栅源电压;Vth是阈值电压;k为玻尔兹曼常数;q为单位电子电荷量;T为绝对温度;VDS为漏源电压;Cox为单位面积栅氧化层电容;μn为载流子迁移率;W/L为宽长比;n与工艺相关的参数。
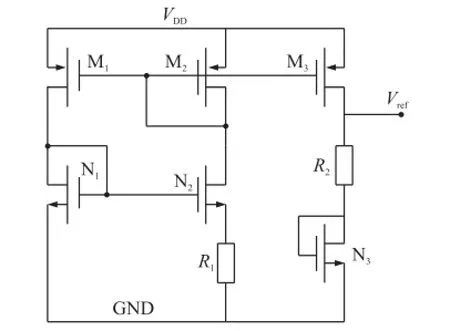
图2 基于MOS亚阈值特性的带隙基准源
当 VDS≫时,式(6)中的最后一项约等于1,可以省略掉,则式(6)可以表示为:
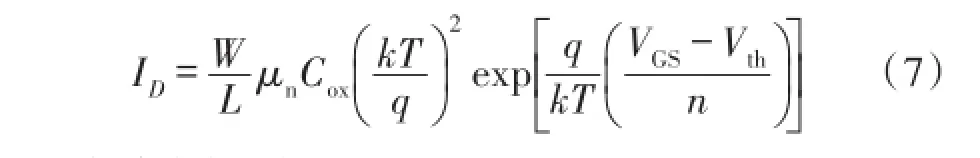
由式(7)可得:

则两个不同MOS管的栅源电压差可以表示为:
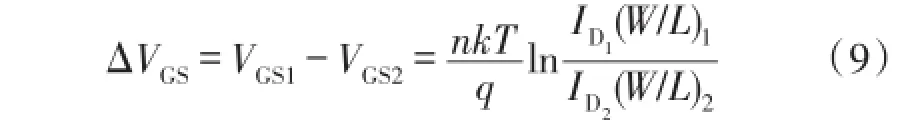
流过电阻R1的电流为:
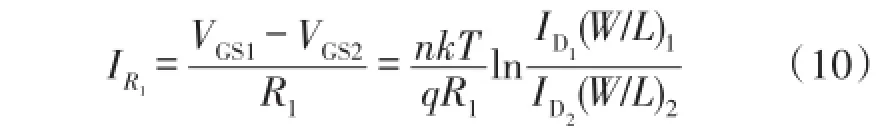
当 M1、M2和 M3的宽长比相等时,即(W/L)1=(W/L)2=(W/L)3,则I1=I2=I3=IR1,那么基准源的输出电压为:
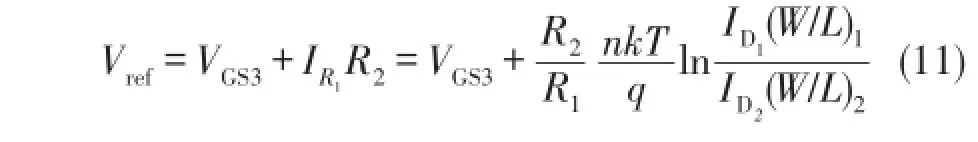
MOS管的栅源电压VGS具有负的温度系数,两个不同MOS管的栅源电压差ΔVGS具有正的温度系数。从式(11)得到通过调整R1和R2,可以得到温度系数较小的Vref。
3 带隙基准源的高阶温度项分析
传统的带隙基准源只是进行一阶温度补偿,而二阶以上的非线性高阶项在高精度基准源中扮演中很重要的作用,为了得到更高精度的基准电压,需对基准源进行高阶补偿。
假如考虑VBE的高阶温度项[5],VBE的表达式可以表示为:
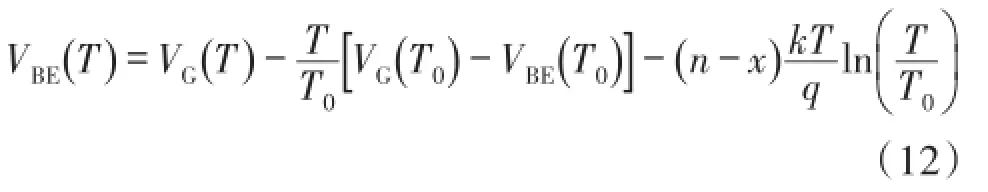
其中T0为参考温度,T为绝对温度,x为集电极电流与温度相关的参数,n是与工艺相关的参数,VG(T)是绝对温度时的带隙电压,其表达式如式(13)所示:
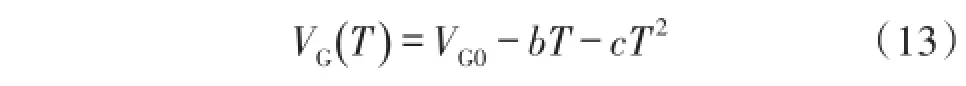
其中VG0、b、c都是正数。当集电极电流Ic与温度成正比例时,式(12)中的x等于1,此时可以得到VBE(T)新的表达式:

把式(14)代入式(5)中,消去一阶温度项,得到Vref的高阶温度项 f()T:
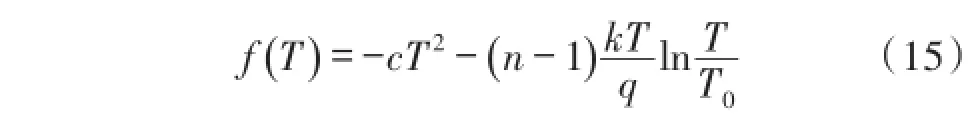
在T0处对f(T)泰勒级数展开得:
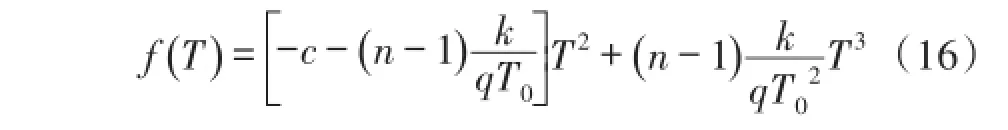
二阶温度项是高阶非线性很重要的部分,n一般的取值在3~4之间,从式(16)中可以看出二阶温度项的系数是负的,因此传统的带隙基准源的输出基准电压曲线如向下的抛物线一样,其曲线如图3(b)所示。
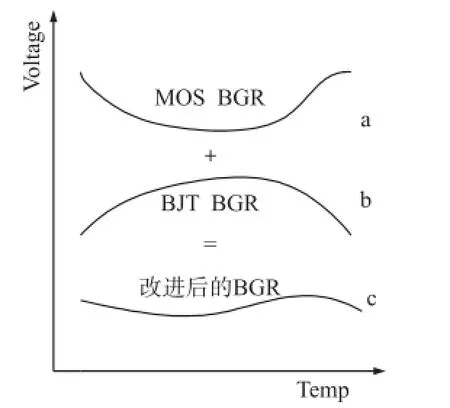
图3 改进型带隙基准源的温度补偿原理图
分析基于MOS阈值特性的基准源的高阶效应,发现主要是受到式(6)中参数n的影响,n是温度的函数,n的泰勒级数展开如式(17)所示:
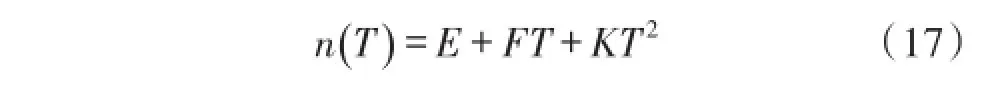
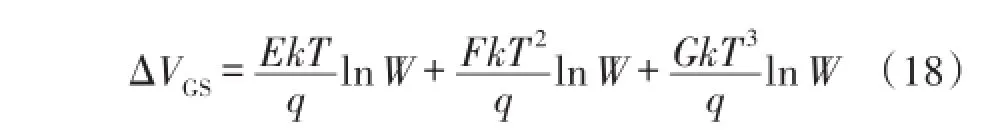
从式(18)中可以看出ΔVGS的二阶温度项系数是正的,因此其温度曲线如二阶向上的抛物线,如图3(a)所示。
4 改进型的带隙基准源
从上述分析发现MOS BGR和BJT BGR具有相反的二阶温度项系数,两个BGR通过适当的权重相加,二阶温度项系数可以消除同时三阶温度项系数减小,补偿原理如图3所示。分析得到ΔVBE具有正的一阶系数,VBE的一阶、二阶、三阶系数都是负的,ΔVGS的一阶、二阶、三阶系数都是正的,因此本设计基于三者合适的权重相加,相互进行补偿,得到改进后的带隙基准源,整个基准源电路由启动电路、带隙核心电路和补偿电路3部分组成,其电路原理图如图4所示。
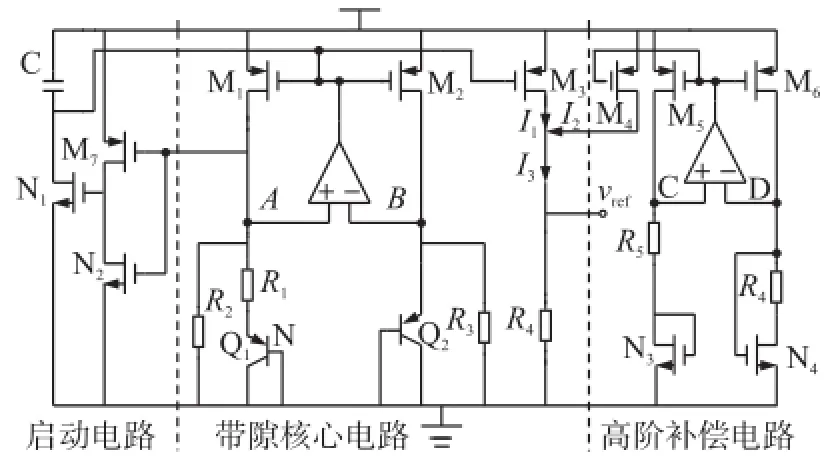
图4 改进型带隙基准源的原理图
在带隙核心电路中,Q1发射极面积是Q2的N倍,运放使得A点和B点的电位相等。(M1-M3)的宽长比相等,即I1为:
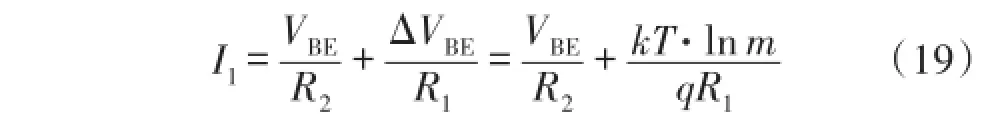
同理,在温度补偿电路中C点和D点的电位相等。(M4-M6)的宽长比相等,N3和N4工作在亚阈区。令
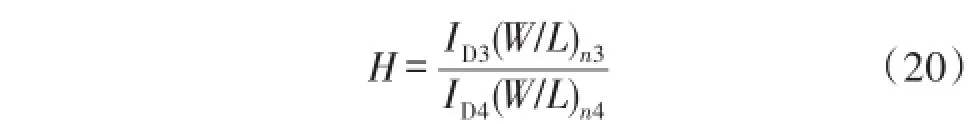
则I2为:
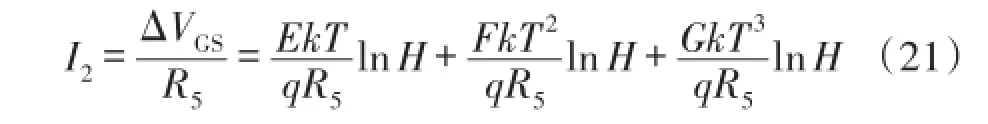
则带隙的输出电压Vref为:
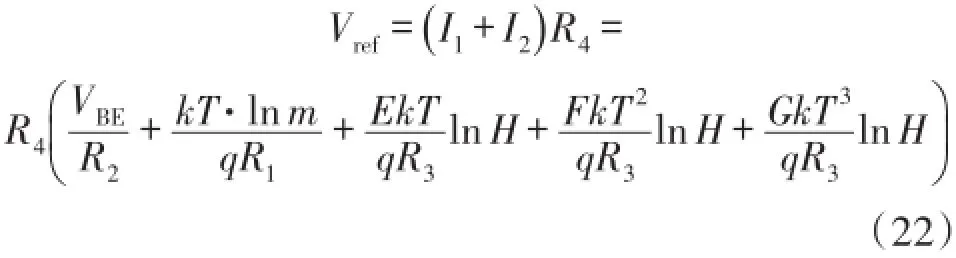
式(22)中VBE具有负的温度系数,而中括号中既包含了正的一阶温度项,也包含正的高阶温度补偿项,通过调整R1、R2、R3可以得到更高精度的基准电压。
4.1启动电路
启动电路原理图如图4所示,由M1、M2和M7以及电容C构成。在电路上电瞬间,C开始充电,M1导通,驱动M1、M2组成的电流镜开始工作。M2、M7共同构成一个反相器,电路稳定后,M2、M7的栅极电压升高,M1栅极电压变为低电平,工作在截止状态,启动电路停止工作。
4.2运算放大器
本设计采用基于电流镜输入的共源共栅放大器,其电路如图5所示。
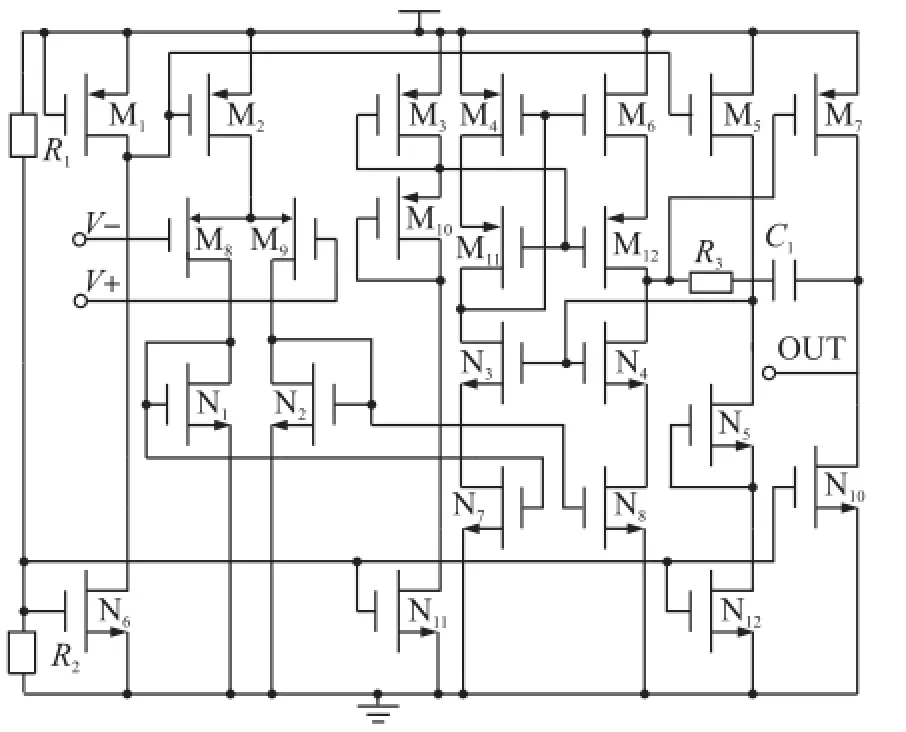
图5 基于电流镜输入的共源共栅放大器
整个运放一共有两级,第1级为基于电流镜输入的共源共栅结构。M8、M9是差分输入对管,M2是尾电流源。N1和N7、N2和N8分别构成电流镜,提高运放的第1级增益。M4、M6、M11、M12构成一个低压共源共栅电流镜。第2级有M7和N10组成,可以增加放大器的输出摆幅。
5 仿真结果与分析
基于 CSMC 0.5 μm标准 CMOS工艺,采用Cadence Spectre对改进型的带隙基准源进行仿真优化。5 V电源电压工作下,对带隙基准源在-40℃~125℃的温度范围内进行扫描。带隙基准输出电压的温度特性曲线如图6所示。
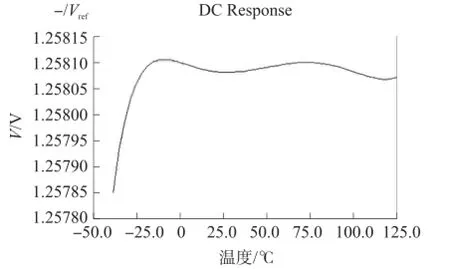
图6 带隙基准输出电压的温度特性曲线
仿真结果表明:其温度系数为1.24×10-6/℃,适用于高精度基准源。
图7为带隙基准的电源抑制比曲线,在低频时PSRR为-68 dB,表明该电路具备良好的电源噪声抑制性能。
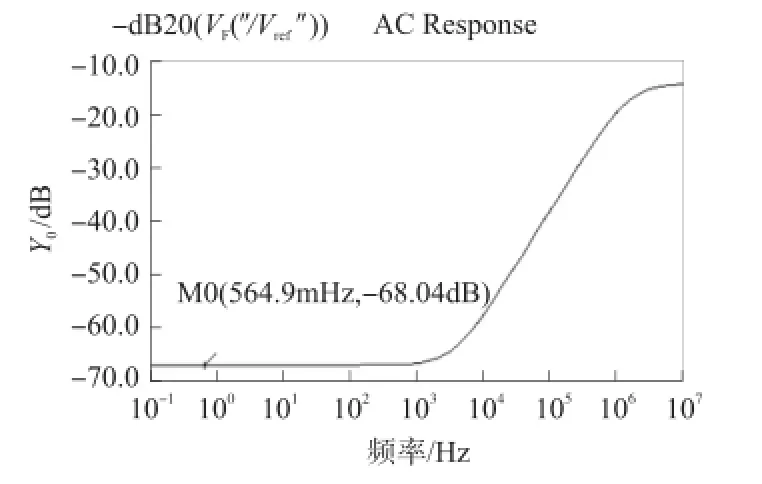
图7 改进型带隙基准的电源抑制比曲线
在27℃室温条件下,对带隙基准进行3.5 V~6.5 V的电源电压扫描,输出电源随电源电压的特性曲线如图8所示,其线性调整率为0.4 mV/V,表明电源电压对基准输出的影响很小。
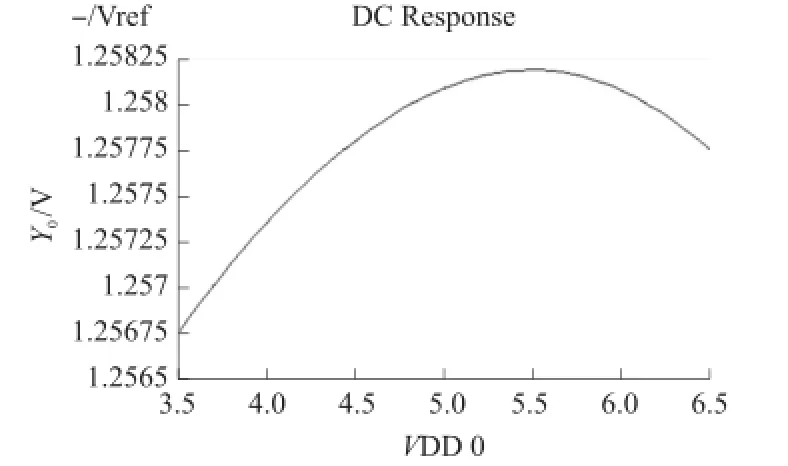
图8 改进型带隙基准的电源特性曲线
表1为本设计改进型的带隙基准源与文献[4]和文献[7]的性能比较结果,改进型的基准源的温度特性和电源抑制能力优于文献[4]和文献[7]。本设计基准源的版图如图9所示。

表1 带隙基准源性能比较

图9 改进型带隙基准源的版图
6 总结
本文通过分析传统的带隙基准源,对带隙基准源进行了改进。利用ΔVBE、VBE和ΔVGS三者的温度特性进行相互补偿,设计高阶温度补偿的高精度带隙基准源。改进后的带隙基准源的性能有了很大的改善,其温度系数1.24×10-6/℃,低频时电源抑制比PSRR为-68 dB,线性调整率为0.4 mV/V,适用于高精度基准源。
[1] Cao Huafeng,Yu Zongguang,Deng Honghui.A Reference Voltage Source and Its Output Buffer for Pipeline ADC[J].IEEE Anti-Counterfeiting,Security and Identification,2014:1-5.
[2] MAndreou C,Koudounas S,Georgiou J.A Novel Wide-Temperature-Range,3.9×10-6/℃ CMOS Bandgap Reference Circuit[J]. IEEE.Solid-State Circuit,2012:574-581.
[3] Linhai Cui.Design of a High Precision Bandgap Voltage Reference[J].IEEE Electronic and Mechanical Engineering and Information Technology,2011:2187-2190.
[4] 代赟,张国俊.一种高性能的亚阈值基准电压源设计[J].微电子学与计算机,2013(5):108-111,116.
[5] Quanzhen Duan,Jeongjin Roh.A 1.2 V 4.2×10-6/℃ High-Order Curvature-Compensated CMOS Bandgap Reference[J].IEEE Circuits and Systems Society,2014:662-670.
[6] 唐宁,李佐,李琦.一种改进的非线性匹配高阶补偿基准源的设计[J].电子器件,2013,36(6):797-801.
[7] 盛诗敏,宋志成,李威.一种基于阈值电压的新型基准电压源设计[J].微电子学,2014(3):293-296,300.
[8] 朱铁柱,张明星,王良坤,等.一种高精度无运算放大器带隙基准源[J].电子器件,2015,38(3):538-542.

陈培腾(1990-)男,汉,广东湛江人,桂林电子科技大学电子与通信工程硕士研究生,研究方向为专用集成电路设计,1060140637@qq.com;

王卫东(1956-)男,汉,桂林电子科技大学硕士生导师,教授,中国通信学会高级会员,研究方向为模拟集成电路与电流模式电路。
A High Precision Bandgap Reference with High-Order Temperature Compensation by ΔVGS
CHEN Peiteng,WANG Weidong*,LI Guanhua
(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin Guangxi 541004,China)
The difference in the gate-source voltage ΔVGSby two MOS that work in the weak inversion,produces the high-end compensation,which carries on high-order temperature compensation for the traditional BJT bandgap reference.A high precision bandgap reference with high-order temperature compensation can be designed by ΔVGS. And the circuit is designed by using CSMC 0.5 μm standard CMOS process.The simulation shows that:when the supply voltage is 5 V,the output reference voltage is 1.258 V;during the range of temperature-40℃~125℃,the temperature coefficient is 1.24×10-6/℃;the PSRR is-68 dB at low frequency;when the voltage works during 3.5 V~6.5 V,linear regulation is 0.4 mV/V.It is suitable for high precision bandgap voltage reference.
bandgap reference;subthreshold;low temperature coefficient
TN432
A
1005-9490(2016)03-0526-05
EEACC:7320G;2570D10.3969/j.issn.1005-9490.2016.03.006

