基于多项式拟合改进的周跳探测方法研究

李克昭，王云凯，赵磊杰，李志伟，魏金本

(河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)



基于多项式拟合改进的周跳探测方法研究

李克昭，王云凯，赵磊杰，李志伟，魏金本

(河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)

多项式拟合法探测周跳因其算法简单，适合计算机编程而被广泛地应用。然而，其探测精度也受到观测误差和采样频率的影响。因此，提出了多项式拟合法结合历元间差分和B-spline 曲线插值法的新方法来解决这两个方面的问题。介绍了新方法的原理和模型，最后利用采集的数据进行了方法验证。

B-spline ；多项式拟合；差分；周跳

在进行精密单点定位时，要达到高精度，就必须保证载波相位观测中没有周跳。而实际测量中，周跳的发生不可避免，因此，就需要一定的方法进行周跳的探测与修复[1]。

在国内外众多工作者多年的研究下，有许多周跳探测与修复的方法在实际中得到了应用。这些方法中包括，高次差法、多项式拟合法、TurboEdit方法、小波法等。但这些方法，有的算法太复杂，有的是受观测误差影响无法完全探测，因此，这些方法在实际测量中的应用受到一定的限制[2-3]。

在众多周跳探测与修复的方法中，多项式拟合法因其算法简单，适合于计算机编程等特点，在周跳探测中被广泛应用[4]。然而，因为拟合精度的限制，多项式拟合法周跳探测的能力受到载波相位观测误差和采样率的影响较大。其中，载波相位观测误差主要受到接收机质量的影响。而采样率对多项式拟合精度的影响可以通过一定的方法进行消除或削弱。对此，应用历元间求差的方法来减少观测误差的影响，然后采用B-spline 曲线插值法进行低频数据的高频化。通过精确的插值计算，解决多项式拟合法在低频数据中拟合误差较大的影响，以充分利用多项式拟合法在周跳探测中的应用优势，提高周跳探测精确度。最后运用采集的相位观测值数据进行了算例分析，验证了该方法的可行性和实用性。

1　多项式拟合法探测周跳基本原理

1.1多项式拟合法周跳探测原理

进行多项式拟合的模型可用以下公式表示[5]：

(1)

其中，i=1，2…m；m≥n+1；ti为拟合的观测历元；t0为初始时间；n为拟合阶数；m为参与一次拟合的历元数。

由于卫星到地球的距离对时间的四阶导数或五阶导数一般已经趋近于零，所以，本文中多项式中的拟合阶数n取4。则式(1)改为：

(2)

在实际计算时，选取前m个没有周跳的观测值代入式(2)，运用最小二乘法解算得到式中的系数的值a0,a1,…,a4，得到一次拟合结果，并根据拟合的残差值vi计算中误差σ。将第m+1个历元代入拟合的曲线中，得到外推的载波相位观测值并与实际值进行比较，如果比较的结果绝对值大于3σ，则判断第m+1历元的相位观测值中包含周跳，并将得到的外推值的整周部分代替观测值中的整周部分，但小数部分不变，从而对第m+1历元的相位观测值进行修复。如果比较结果的绝对值小于3σ，则判断第m+1历元没有发生周跳，则不用进行修复,并对求差值前的历元的观测值进行修复处理。经过比较判断后，舍弃第一个历元的观测值，加入第m+1历元的修复的观测值，代入式(2)，进行下一历元的判断。然后继续以上过程，直至最后一个观测值为止。

1.2方法改进

由接收机上直接读取的相位观测值，其中包含了许多误差，主要包括：接收机钟差、卫星钟钟差、电离层延迟、对流层延迟、多路径等。对于这些误差可以利用差分的思想进行消除或减弱,最简单的方法是将卫星接收的相位观测值进行历元间求差[6]，将求差后的观测数据进行多项式拟合，其拟合模型可表示为:

△φi=b0+b1(ti-t0)+b2(ti-t0)2+b3(ti-t0)3+b4(ti-t0)4

(3)

其中，△φi=φi+1-φi。

通过历元间求差，电离层延迟、对流层延迟、多路径等误差基本被消除，且在两个历元间短时间的观测中其他各种误差变化值非常小，可以忽略，进而有利于多项式拟合的进行。

2　B-spline曲线插值原理

由于相位观测值的观测时间是等间隔的，可以用等参数三次均匀B样条曲线拟合进行插值，其模型为[7-9]：

(4)

其中，V1，V2，…，Vn+2为控制定点；函数Gj(t)为基函数且满足以下条件：

(5)

其中，t[0,1]。

将式(5)代入式(4)，写成矩阵形式为：

(6)

其中，i=1,2,…,n-1。

由式(4)、式(5)和式(6)可知，对于给定的n个观测历元的相位观测值，由n-1段曲线进行拟合，其中第i段的首末观测值和控制定点的关系为：

(7)

为了避免边界问题，令首末两个观测值和控制多边形的首末顶替重合，并将第2个和第n-1个观测值作为插值曲线的首末端点，则得到以下方程：

(8)

通过式(8)可以反算出控制顶点Vi(i=1,2,…,n)，将其代入到式(4)中可求出通过已知坐标点的内插后的三次均匀B样条曲线。

3　综合B-spline插值和多项式拟合法进行周跳探测

为了消除或削弱接收机钟差、电离层等的影响，在前述第1节中进行了历元间的差分，使得到的观测值中电离层延迟、对流层延迟、多路径等被削弱，而其他各种误差的变化值也非常小，可以忽略。这样更有利于进行多项式拟合，提高了拟合的精度。

由文献[6]可知，多项式拟合法探测周跳受载波相位观测值误差和采样频率的较大影响，应用历元间差分削弱了观测误差，而对于采样频率的问题，则可利用B-spline 曲线插值法将低采样频率的载波相位观测值插值到1s或者0.1s等较高的采样频率，这有助于提高的拟合精度。但是，当插值出的采样频率过高时，将会增加计算量，对于计算不利。基于此，并结合文献[10]，将低采样频率的观测值通过插值法插值到1s，在不增加观测噪声的情况下达到了高采样率。

对于多项式拟合，拟合时运用的数据越多，则得到的拟合结果越精确。周跳探测时，首先进行历元间求差，组成新的观测序列；提取前m个没有周跳的观测值，运用B-spline 曲线插值法进行插值，将其插值到1s的采样频率；将插值后的数据代入式(3)，求出拟合系数，并计算中误差σ；利用求得的多项式拟合系数外推下一历元的相位观测值，并将外推值与实际值进行比较，判断是否产生了周跳；对含有周跳的历元利用前述1.1节的方法进行修复；然后继续上述过程，直到最后一个观测历元。

4　算例分析

为验证改进方法的可行性和有效性，选取了IGS站在2015年2月11日提供的G23卫星的相位观测值数据作为实验数据进行处理分析。利用TEQC软件进行检验，原始观测值中没有周跳。

首先对采样率为1s的观测数据进行处理得到外推值与实际值之间的偏差如图1所示。

由图1可以看出，运用提出的新方法进行数据的处理，得到的外推值与实际值之间的偏差绝对值大部分小于0.13周，可以探测出1周以内的周跳。

运用TEQC软件将此组数据生成采样率分别为15s 、30s的观测数据，运用新方法进行数据处理，得到的外推值与实际值之间的偏差如图2、图3所示。

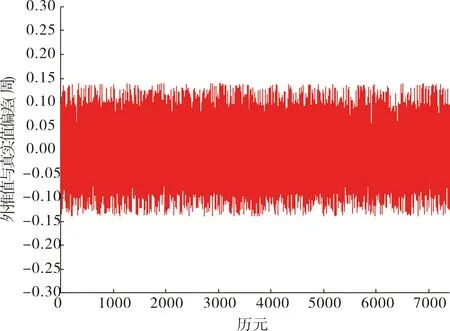
图1　采样率为1s的观测数据外推值与实际值之间的偏差

图2　采样率为15s的观测数据外推值与实际值之间的偏差

由图2、图3可以看出，运用新方法将15s、30s的观测数据进行插值处理，得到的外推值和实际值之间偏差的绝对值在0.15周以内，精度较高，对1周以上的周跳，可以进行探测。为检验插值后的多项式探测周跳的性能，在差分数据中人工模拟加入周跳，然后利用新方法进行周跳的探测。其中在采样率为1s的第50 、2 500和4 500历元处分别加入1周、10周和-10周的周跳；在采样率为15s 、30s的观测数据中的第50 、100和150历元处分别加入1周、10周和-10周的周跳。加入人工模拟周跳后，在不同采样率下利用多项式拟合结合B-spline 曲线插值法进行探测周跳，其结果如图4所示。

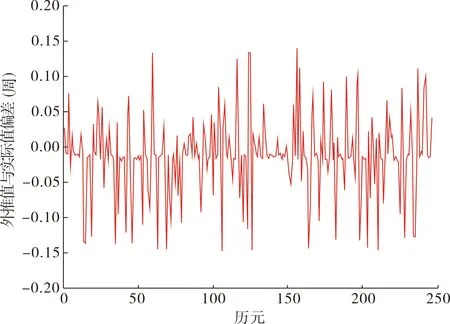
图3　采样率为30s的观测数据外推值与实际值之间的偏差

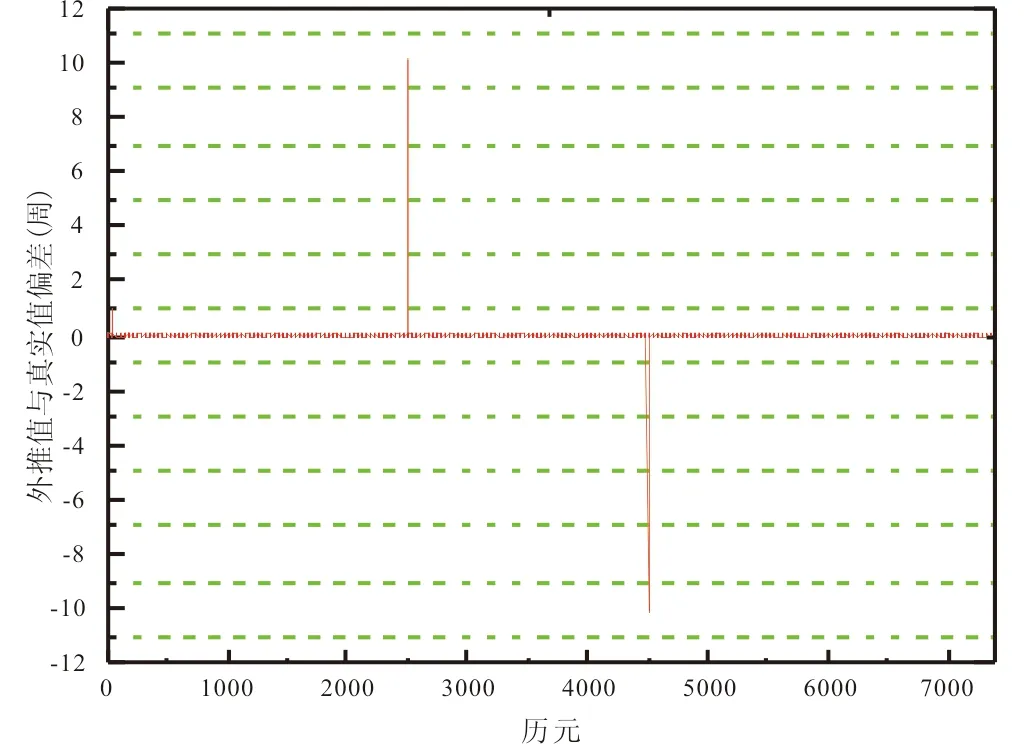
(a) 采样率为1s的观测值的周跳探测

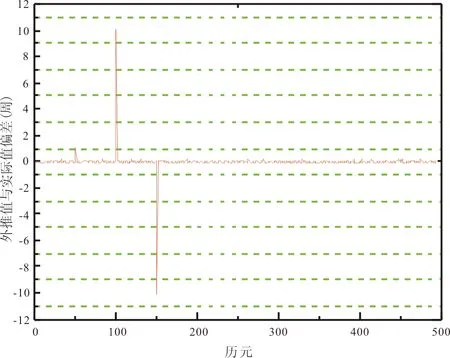
(b) 采样率为15s的观测值的周跳探测

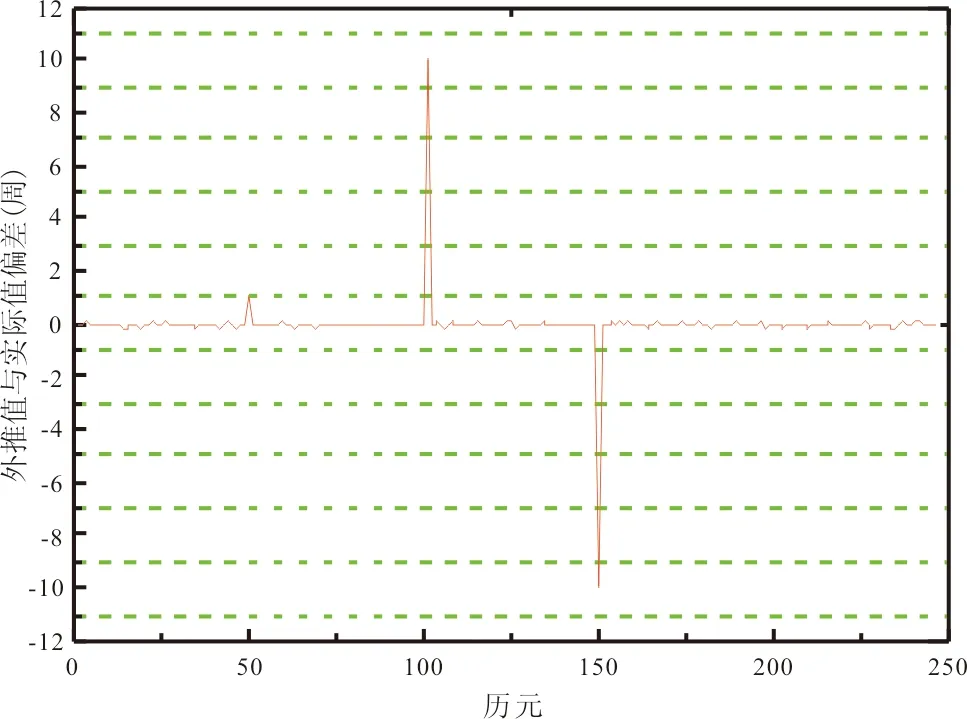
(c) 采样率为30s的观测值的周跳探测

从图4中可以看出，对于人工加入的模拟周跳，新方法都能够准确的探测出来。因此，将15s 、30s采样率用于多项式系数求解的m个数据通过B-spline 曲线插值法插值到1s的数据采样频率，其结果能够探测1周以上的周跳并修复。

5　结论

提出的基于多项式拟合结合B-spline 曲线插值法进行周跳探测的方法可以探测出1周以上的周跳并修复。利用历元间求差的方法，既大大的削弱了电离层延迟和对流层延迟的影响，提高了观测值的精度，同时也降低了数据的位数，减少了数据的计算量，更有利于计算编程。通过对低频数据中每次拟合的前m个观测值进行B-spline 曲线插值，增加了拟合的数据，使得拟合更为精确，提高了周跳探测的能力。

由于本文采用的数据为IGS站提供的数据，而IGS站的观测仪器及其观测环境都比较优越，因此，其周跳的探测结果较为理想化。对于实际测量中，应根据测量环境的不同，采用不同的插值频率，以更好地适应实际测量情况，进行周跳的探测和修复。

[1]李克昭,扬力,柴霖，等.GNSS定位原理[M].北京：煤炭工业出版社,2014.

[2]Cai C,Liu Z,Xia P,Dai W.Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity[J].GPS Solution,2013,17(2):247-260.

[3]扬剑,李江卫,吴浩，等.单频GPS 非连续历元周跳处理研究[J].测绘科学,2013,38(4):59-61.

[4]罗峰,姚宜斌,宋伟伟.综合利用多项式拟合和载波相位变化率探测单频GPS周跳[J].全球定位系统，2007,32 (5):9-13.

[5]李征航,黄劲松,张勤.GPS测量[M].武汉：武汉大学出版社, 2013.

[6]原波,白征东,付春浩.一种基于多项式拟合法的新的单频周跳探测方法[J].工程勘察,2011,39(12):63-66.

[7]R Talebitooti,MH Shojaeefard,S Yarmohammadisatri.Shape design optimization of cylindrical tank using b-spline curves[J].Computers & Fluids,2015,109:100-112.

[8]王娟,李学鹏.基于三次B样条曲线的未标定分层重构[J].计算机与数字工程,2015(8):1511-1515.

[9]李涛,漆泰岳,王睿,等.三次B样条在隧道断面拟合中的应用研究[J].铁道标准设计,2015, 59 (8):127-130.

[10]张勇.GPS载波相位周跳探测实验总结报告[R].2012:42-66.

A new modified cycle-slips detection method based on polynomial fitting method

LI Ke-zhao,WANG Yun-kai,ZHAO Lei-jie,LI Zhi-wei,WEI Jin-ben

(SchoolofSurveyingandLandingInformationEngineeringofHenanPolytechnicUniversity,Jiaozuo454000,China)

The polynomial fitting method is used widely to detect cycle slip for its easily computer programming and simple algorithm.As for its accuracy,it is restricted by the observation errors and the sampling rate.A new method which combines with polynomial fitting method and the B-spline curves interpolation is presented in this paper.This paper introduces the mathematical theory and model.And finally a test is made to show the reliability of this new method.

B-spline;polynomial fitting method;difference;cycle-slip

2015-12-20

国家自然科学基金资助项目(41202245；41272373)

李克昭(1977—)，男，甘肃靖远人，博士，副教授。

王云凯(1988—)，男，河南淮阳人，硕士研究生。

1674-7046(2016)03-0063-06

10.14140/j.cnki.hncjxb.2016.03.012

P228.1

A