对随机性复合标底法投标报价策略的研究

黄朝煊,方咏来,袁文喜,李水泷,赵　勇

(浙江省水利水电勘测设计院,浙江 杭州　310002)



对随机性复合标底法投标报价策略的研究

黄朝煊,方咏来,袁文喜,李水泷,赵勇

(浙江省水利水电勘测设计院,浙江 杭州310002)

摘要：基于博弈论中的混合战略纳什均衡,采用概率理论和数值分析理论研究随机性复合标底法中最优投标报价,利用二次多项式等效非线性函数,给出连续型随机性复合标底法下最优报价的解析计算式,对于离散型随机性复合标底法可采用连续型等效,也可采用枚举法结合Matlab编程求解,通过工程实际竞标案例,验证该理论具有极好的工程实际应用价值。

关键词：随机性复合标底法;混合战略纳什均衡;投标报价策略;最优报价;解析计算式

招投标包含招标和投标2种形式,招标和投标是商品交易方式[1],是市场经济中交易过程的2个方面,也是国际惯例。招标投标活动中的主要参与人是招标人和投标人。

工程投标报价理论由Emblem[2]提出， 随后Friedman[3]发表了投标报价的研究成果，众多学者在Friedman基础上提出了多种模型，如：Gate模型[4]、Carr R I模型[5]等，其研究方法均采用决策和对策论，但模型的假设约束条件很强，在工程实践应用中存在较大缺陷。

胡军峰等[6]将博弈论应用于电力需求价格的均衡分析中;卢德林等[7]对土建工程报价优化模型进行了研究,但对随机性因素的考虑均不足；阮连法等[8]将博弈论理论应用到建筑工程投标报价中,但模型过于简单,不便于实际投标报价应用;胡静[9]对多家企业投标报价状况进行调查分析,并对复合标底法建立了简易投标报价模型,但该模型对投标参与者的相关历史信息要求有充分了解,与工程实际不符。欧阳益[10]也对复合标底法进行了初步研究,认为所有投标人报价均理性地朝最接近复合标底的最高分值贴近。

以上学者的研究均未涉及常用的随机性复合标底法,因此,笔者基于博弈论中混合战略理论,对随机性复合标底法投标报价策略进行了研究。

1　随机性复合标底法

随机性复合标底法在复合标底中增加了随机性,使得招投标更公平公正,其中随机性复合标底法中复合标底计算公式

(1)

(2)

式中:C为评标中的复合标底;A为业主的期望标底,一般在开标现场以随机摇号法确定,取值范围为A∈(a1,a2),记其概率密度函数为:f(A);β为业主在开标现场以随机摇号法确定的权重系数,取值范围为β∈(β1,β2), 记其概率密度函数为:g(β);Bi为第i家投标单位的报价,取值范围在业主规定的报价范围内,即Bi∈(Bmin,Bmax);n为投标单位的总个数;μ为最优报价下浮率,暂取μ=0。

2　混合战略理论在随机性复合标底法中的应用

2.1 随机性复合标底投标报价博弈模型

随机性复合标底投标报价博弈模型的建模要求是根据投标人竞争信息情报、战略、报价效用等,利用博弈规则预测报价均衡,确定最优的报价,其基本框架为:

a. 参与人:有n个投标人参加投标。

b. 信息:对业主及投标竞争对手的信息完全互相不了解。

c. 战略:报价是每个投标人自己的战略,所有投标人的报价均在业主规定范围Bmin≤Bi≤Bmax。

d. 博弈规则:评标中评分标准为随机性复合标底法,复合标底由业主设定的随机标底与所有投标人有效报价按照随机权重系数复合确定(式(1)),最优报价为复合标底按下浮率μ计算确定报价(本文暂取μ=0),投标人报价等于最优报价得满分;投标人报价高于最优报价每1%扣1分;低于最优报价每1%扣0.5分(实际招标中扣分值可能会不尽相同,但一般高报价的扣分值会大于低报价)。

e. 效用:工程实际竞标中一般具有唯一性,即只有唯一中标人。

f. 投标人报价目的:在报价不低于当前市场成本的情况下获得最高报价得分,即报价最接近于最优报价,则投标人i报价Bi的支付为

(3)

式中：ui为投标人i报价Bi时的支付函数(得分);h为投标报价满分。

以上即为随机性复合标底的投标报价博弈模型。投标人i的关键任务是对最优报价D进行预测,使得自己的报价得分最高,这个最优报价对所有投标人是均等的,即存在稳定的纳什均衡。

2.2随机性复合标底投标报价博弈模型的纳什均衡解的存在性

纳什均衡，即非合作博弈均衡。纳什均衡分成两类：纯战略纳什均衡和混合战略纳什均衡，笔者研究的随机性复合标底投标报价博弈模型属于混合战略纳什均衡。

根据纳什均衡的3条存在性定理[11]，以及工程实际中投标竞标的特征，奠定了建筑及水利工程投标报价的博弈均衡解存在性的理论基础。

2.3 随机性复合标底投标报价博弈模型的混合战略纳什均衡解的求解

对于连续型变量,当业主期望的随机标底在A∈(a1,a2)范围内按一定概率分布随机变动、随机权重系数在β∈(β1,β2)范围内按均布概率随机变动时,即所有投标人均朝着最优报价目标报价,第i个投标人报价Bi的计算报价评分期望值为

(4)

(5)

式中:H为投标人i报价等于最优报价D时的支付值;F(Ai)为业主期望标底Ai相应的概率密度分布函数;g(βi)为权重系数β连续概率密度函数。

(6)

D3+b2D2+b1D+b0=0

(7)

(8)

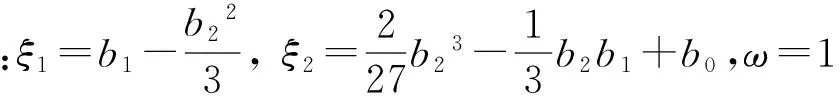
对于离散型随机变量,可通过Matlab软件列举法求解,也可以采用连续型等效,关键是采用连续型概率分布等效离散概率分布,其最优报价D值解基本一致的。

3　案例分析

3.1案例

沿海地区某围涂项目总围垦面积约2 800 hm2,海堤总长23.6 km、排涝水闸7座、交通隔堤及配套工程等。

a. 发包范围:初步设计、招标设计、施工图设计。内容包括初步设计报告、招标图纸及技术条款和工程量清单、施工图等。

b. 质量要求:符合国家规定及技术规范要求。

c. 招标人的工程总设计费测算价(最高限价)为1 283万元。其中投标报价评分细则为:①最佳报价值=业主期望标底×(调整系数)%+符合条件的报价平均值×(100-调整系数)%;②符合条件的报价区间以招标人测算价1 283万元(含)为上限,以测算价下浮8%为下限(取整数1 180万元,含本数)；③业主期望标底为1 150万～1 250万元(1 150、1 160、1 170、1 180、1 190、1 200、1 210、1 220、1 230、1 240、1 250)中随机抽取的1个数；④调整系数从0～4(0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0)中随机抽取的3个数的平均值,保留二位小数；⑤报价得分评判原则为报价等于最佳报价值的得满分60分，报价每低于最佳报价值1个百分点扣0.5分，报价每高于最佳报价值1个百分点扣1分，报价得分不足一个百分点时,使用直线插入法计算,保留二位小数。报价最低得分为56分。其中,低于报价区间下限的投标报价为有效报价,但不作为计算报价平均值的基础。当所有报价均低于报价区间下限时,则以报价区间下限1 180万元为报价平均值。

3.2模型建立与求解

根据招标文件可知,业主期望标底A在1 150万～1 250万元之间满足均布概率分布,调整系数β为0 ～ 4(0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0)中随机抽取的3个数的平均值,根据排列组合理论可知,调整系数β的概率分布如图1所示。

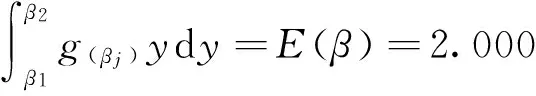
若采用连续函数等效离散的调整系数β的等效连续型概率密度函数为

Pβ=5.963×β(4-β)(3.65×10-3β4-2.92×10-2β3+

0.071β2-0.051β+0.0172)

根据本文解析计算理论可知,投标人最优报价为D=1 213万元,见图2。

最终开标结果为:①业主的期望标底通过摇号确定为A=1 190万元；②β通过摇号获得3个数(2.5、1.0、1.5),即确定β=(2.5+1.0+1.5)/3=1.667。③根据招标文件确定最终的最优报价为:1 205.73万元。

图1　调整系数β的概率分布

图2　投标人不同报价下的支付函数关系曲线

依据招标文件评分细则,计算各投标人得分(表1)，最终投标人甲以1210万元报价获得最高分,并中标,说明该理论具有较好的工程应用价值。

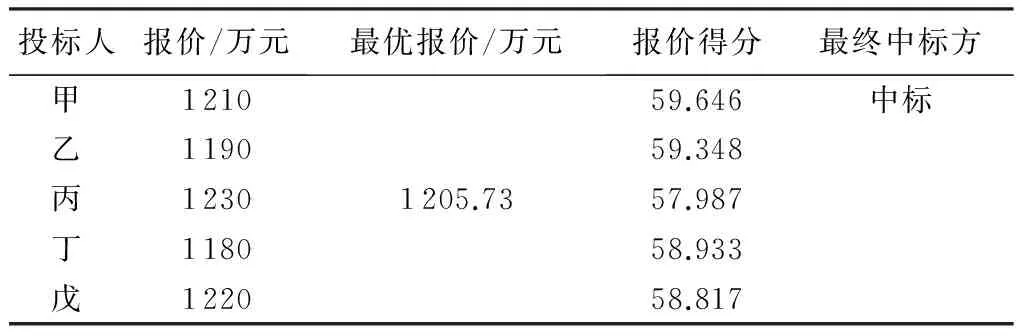
表1　最终开标结果统计

4　结　语

随机性复合标底法以其特有的公平公正性,在工程实际招标中被普遍采用,笔者基于博弈论中的混合战略纳什均衡为理论基础依据,对随机性复合标底法中最优投标报价进行了研究,主要结论如下:

a. 依据博弈论和概率理论建立了随机性复合标底法投标报价模型,依据最大支付值原理给出了连续型、离散型随机性复合标底法的最优报价计算方程。

b. 利用数值分析理论及二次多项式等效非线性函数,根据数值极值理论给出了最优报价的一元三次方程,并采用卡当公式直接给出了连续型随机性复合标底法下最优报价的解析计算式。对于离散型随机性复合标底法可采用连续型等效,也可采用枚举法结合Matlab编程求解。

c. 最后通过某工程实际竞标案例,验证了该理论具有极好的工程实际应用价值。

参考文献：

[ 1 ] 宁素莹.建设工程招标投标与管理[M].北京:中国建材工业出版社,2003.

[ 2 ] EMBLEM D.Competitive bidding for corporate securities[D].New York: Dissertation,Colubia University,1944.

[ 3 ] FRIEDMAN L.A competitive bidding stratege [J].Operation Research,1956,4,104-112.

[ 4 ] GARES M.A didding strategy based on ESPE [J].Cost Engineer,1983,25,27-35.

[ 5 ] CARR R I.Competitive bidding and opportunity costs[J].Journal of Construction Engineering and Management ASCE,1987，113(6)：151-165.

[ 6 ] 胡军峰,李春杰,赵会茹,等.基于博弈论的电力需求价格弹性与发电市场均衡关系[J].中国电机工程学报,28(1):89-94.

[ 7 ] 卢德林,章祥荪,马桂芝.土建工程报价优化模型[J].系统工程理论与实践,2002,22(9):47-53.

[ 8 ] 阮连法,匡亚萍,吴显.博弈论在建筑工程投标报价中的应用[J].建筑经济,2002(6):26-28.

[ 9 ] 胡静.基于博弈论的施工企业投标报价行为研究[D].杭州:浙江大学,2004.

[10] 欧阳益.工程项目投标报价的研究[D].苏州:苏州大学,2006.

[11] 谢识予.经济博弈论 [M].上海:复旦大学出版社,2006.

基金项目：水利部公益性行业科研专项(201401010)

作者简介：黄朝煊(1983—),男,湖北黄石人,工程师，硕士,主要从事水工结构及岩土工程研究。E-mail: 516227811@qq.com

DOI：10.3880/j.issn.1003-9511.2016.04.004

中图分类号：F284

文献标识码：A

文章编号：1003-9511(2016)04-0013-04

(收稿日期：2015-12-03编辑：方宇彤)