基于模糊逻辑的多尺度小基高比立体匹配方法

马宁，门宇博，李香，门朝光(.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨，5000；2.哈尔滨师范大学 计算机科学与信息工程学院，黑龙江 哈尔滨，5000)

基于模糊逻辑的多尺度小基高比立体匹配方法

马宁1,2，门宇博1，李香1，门朝光1
(1.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨，150001；
2.哈尔滨师范大学 计算机科学与信息工程学院，黑龙江 哈尔滨，150001)

针对小基高比立体匹配中的辐射差异和深度精度问题，提出一种小基高比立体匹配方法。该方法首先通过小波变换对立体图像构建多尺度空间，然后利用HSL色彩模式下的模糊逻辑相似性测度函数和十字支撑臂自适应窗口技术获取初始匹配成本，再依据“胜者全取”策略计算整数级视差，最后以整数级视差为基础利用基于迭代相位相关法的亚像素匹配方法计算亚像素级视差图。研究结果表明：该立体匹配算法克服了小基高比匹配中的辐射差异问题，同时获得了高精度亚像素级视差，其亚像素精度高于1/20个像素。

立体匹配；小基高比；自适应窗口；模糊逻辑；亚像素视差

立体匹配是计算机视觉领域的研究热点，它利用不同视角下图像的视差，根据三角测量原理获取场景三维信息。基高比是指摄影基线长度与摄像机高度的比值，根据基高比的差异可将匹配方法分为大基高比立体匹配方法和小基高比立体匹配方法。按文献[1]的分类标准，大基高比立体匹配方法又可分为局部匹配和全局匹配。局部方法以自适应权重[2]和自适应窗口[3]为代表算法，具有较高的准确率和效率。全局方法利用动态规划(dynamic programming,DP)[4]、置信传播(belief propagation, BP)[5]和图割(graph cut,GC)[6]等算法将匹配问题转为求解能量最优化问题，可获得更高质量的视差结果。大基高比图像存在较大遮挡和几何畸变等不利因素影响相关匹配，为减弱上述不利因素对匹配的影像，小基高比立体匹配技术应运而生。小基高比图像具有视角变化小，遮挡少、几何畸变和阴影变化不明显等优点，但小基高比会造成深度精度的损失，因此，在小基高比立体匹配中视差的量测精度必须达到亚像素级别以弥补这部分损失。DELON 等[7]提出小基高比立体匹配方法，该方法通过概率密度函数自适应调节支撑窗口保障了匹配的准确率，但由于相似性度量采用基于灰度的规范化互相关方式，该方法在辐射差异条件下误差较高，另外形状单一的支撑窗口导致前景物体边界膨胀；门朝光等[8]提出基于迭代传播的小基高比匹配法，该算法通过求解相关基本等式减少了文献[7]中存在的膨胀现象；范大昭等[9-10]提出基于相位相关的小基高比匹配算法获得了较高的视差精度，但侧重于研究靶标的亚像素视差，没有对稠密匹配模式进行探究。为有效解决小基高比立体匹配中辐射差异问题，同时获得高精度稠密的亚像素级视差图，本文作者提出一种基于模糊逻辑的多尺度小基高比立体匹配方法。该方法通过将模糊逻辑相似性测度函数和自适应窗口技术相结合以解决辐射差异条件下的立体匹配问题，同时为克服小基高比对深度精度的影响，采用一种基于迭代相位相关法的亚像素级匹配方法计算高精度的亚像素级视差图。

1　算法框架

本文提出的基于模糊逻辑的多尺度小基高比立体匹配方法处理的是经过极线校正的立体图像，并最终输出稠密的亚像素级视差图。该方法首先通过小波变换为立体图像构建多尺度空间，再根据HSL色彩模式下的模糊逻辑相似性测度函数和自适应窗口技术获取初始匹配成本，然后利用“胜者全取”策略计算整数级视差，采用模糊集理论构建测度函数可以有效地压制辐射差异带来的影响。最后在整数级视差基础上，利用基于迭代相位相关法的亚像素级匹配方法获得亚像素级视差图。基于模糊逻辑的多尺度小基高比立体匹配算法的整体流程如图1所示。

图1　匹配算法流程图Fig.1　Flow chart of proposed stereo matching algorithm

2　算法的关键步骤及实现

2.1基于小波变换的多尺度空间构建

多尺度空间是一种由粗到精的匹配思路：首先对图像多分辨率分解，按分辨率由粗到精的顺序自上而下构造多尺度空间；从空间顶级开始逐级向下匹配，将高一级图像匹配结果作为约束条件，指导低一级尺度图像的匹配过程，最终到达最低一级对原始分辨率图像进行匹配。视差变化范围随尺度的增加而减小，各尺度间的视差满足dk=d/2k，其中k为尺度级别，d为原始图像视差。小波变换具有良好的多尺度特性，设f( x1, x2)为原始分辨率图像，是一组K层多尺度空间图像，φ(x1, x2)和ψ(x1,x2)为相应尺度函数和小波函数，则f(x1,x2)的多尺度空间表达式为

式(1)右侧第1项表示原始图像在多尺度空间的低通滤波信号，系数C为f的离散平滑逼近；第2项为3个带通滤波细节。以两级尺度空间为例，如图2所示，经小波分解后空间中第k-1层图像的低频部分LLk-1可表示为：k层的低频部分LLk和水平、垂直、对角线3个方向上的高频成分HLk，LHk和HHk。

图2　小波多尺度空间示意图Fig.2　Schematic diagram of wavelet based multiscale space

多尺度空间中任意相邻2层图像k与k-1之间的视差传播方式为：k层图像中的任意像素点(u,v)对应了k-1层图像中的4个像素点(2u,2v)，(2u+1,2v)，(2u,2v+1)和(2u+1,2v+1)。假设(u, v)点的匹配像素点为(u',v')，则(2u,2v)点可能匹配的像素为(2u',2v')，(2u'+1,2v')，(2u',2v'+1)和(2u'+1,2v'+1)，任意相邻2层图像k与k-1之间的视差传播公式为

式中：dk-1(2u,2v)表示k-1层图像在(2u,2v)像素点处的视差结果；dk(u, v)为k层图像在(u, v)像素点处的视差结果；Δd为(0,0)，(0,1)，(1,0)，(1,1) 这4项中使匹配成本最小的一项。

2.2基于模糊逻辑的相似性测度函数

为了克服匹配中的辐射差异问题，本文提出一种基于模糊逻辑的测度函数来判断像素点间的相似性。HSL色彩空间中颜色被定义为色度，饱和度和光度3个分量，ΔH，ΔS和ΔL表示各分量的差异。基于模糊逻辑的相似性测度函数包括2步。

第1步：为相似性测度函数建立模糊集。模糊逻辑模型ΔH和ΔS各有4个模糊集，分别被定义为和，由于ΔL表示光度差异，对于存在辐射差异的立体图像，光度不应作为重要的判别依据，故ΔL只定义2个模糊集{ls, ll}。模糊集隶属度函数表达式为

图3　模糊隶属度函数Fig.3　Fuzzy membership functions

第2步：为相似性测度函数建立模糊规则。

规则1：若ΔH，ΔS和ΔL均较小，则2个像素点具有高相似度。

规则2：若ΔH，ΔS和ΔL中有1个变量较大，则2个像素点相似度较低。

上述2个规则的值域为(0,1)，其中：0代表两像素点相同，1代表两像素点不同。基于模糊逻辑的相似性测度函数FR的数学表达式为

式中：μH， μS和μL分别为H，S，L 3个分量的模糊集隶属度函数值。应用模糊相似性测度函数对参考图像像素点(u, v)与目标图像视差为d的对应像素点(u+d, v)计算匹配成本的表达式为

式中：μset(u, v, d )H，μset(u, v, d )S和μset(u, v, d )L表示参考图像像素点(u, v)与目标图像像素点3个分量差值的隶属度函数值。将立体图像的全体像素点初始匹配成本C( u, v, d)保存在视差空间图DSI中，作为后续步骤的输入数据。

2.3基于十字支撑臂的自适应窗口策略

本文根据文献[3]方法提出一种改进的成本累积策略对初始匹配成本C( u, v, d)进行聚合，窗口由同列相邻像素扩展水平方向线段组成。该累积策略具有2个优点：1)支撑区可以根据颜色相似度构造任意的形状和尺寸，更加贴合物体边界；2)成本累积过程可以利用积分图像加速技术在常数时间内完成。基于十字支撑臂的自适应窗口成本累积包括以下2个步骤：

以十字臂为基础，扩张成支撑窗口U(p)。U(p)由垂直臂V(p)和沿V(p)滑动的多条水平线段H(q)组成，其数学表达式为

图4　基于十字支撑臂的自适应窗口成本累积Fig.4　Graphic illustration of cross-based aggregation

第2步：累积支撑窗口内的初始匹配成本。为避免异常像素对累积的影像，采用对称方式确定像素点p的臂长lp：

最后利用“胜者全取”(winner take all,WTA)策略计算最优视差，其视差计算公式为

2.4基于迭代相位相关法的亚像素匹配

图5　亚像素级匹配算法流程图Fig.5　Flow chart of sub-pixel matching algorithm

基于迭代相位相关法的亚像素级匹配方法的详细步骤如下。

1)根据整数级视差，确定参考图像像素点p0( u, v)在目标图像的对应点，d为整数视差。以p0和 q0为中心，截取大小为w× h的子图像与。

3)利用窗口函数为子图像加窗，并计算加窗后2幅子图像的相位相关函数。设F( u, v)和G( u, v)分别为f( x, y)与g( x, y)的离散傅里叶变换，则二者的相位相关函数Q可表示为

4)对Q( u, v)作逆傅里叶变换并定位峰值位置，以峰值为中心选取5×5元素区域进行曲面拟合，计算峰值与中心的亚像素级偏移量。

3　实验分析

实验使用2组带有高程信息的小基高比立体影像对，如图6所示。图6(a)所示为2组立体影像对的左视角图像，图6(b)所示为2组立体影像对的右视角图像，简称左图像和右图像。在成像过程中，基高比约为0.05，地面分辨率R=0.3；为验证本文算法对辐射差异的鲁棒性，对右图光照条件进行调整。图6(c)和(d)所示分别为水平、垂直方向辐射差异图，光强呈梯度变化，范围由-50%增加到+50%；图6(e)所示为真实视差图。图7(a)，(c)和(e)所示分别为本文算法在无辐射差异、水平、垂直方向辐射差异3种条件下计算的视差图，图7(b)，(d)和(f)所示为文献[7]描述的MARC算法在上述条件获取的视差图。从图7可以看出：MARC算法随辐射差异的增加视差图质量下降，物体边界处产生明显的膨胀现象。这是由于匹配度量采用互相关函数，该函数对辐射差异较敏感，累积窗口只改变窗口尺寸而不改变形状，导致窗口跨越物体边界，违背了前视平坦假设。从图7(a)，(c)和(e)可以看出：本文算法获得的视差图质量没有随辐射差异增加而下降，建筑物的边界非常清晰，基本上与建筑物原始尺寸一致，本文算法所获得结果明显优于文献[7]的实验结果。但是本文和文献[7]均采取局部成本累积策略，在大面积弱纹理区域匹配误差较大。为了量化比较算法性能，图8所示为本文算法、文献[7]和文献[8]算法误匹配率量化实验结果。从图8可以看出：随立体图像之间辐射差异的增加，本文算法所获得的视差图误匹配率仍然相对较低，而其他2组实验数据误匹配率则明显增加。本文算法亚像素级视差精度根据高程精度验证，高程计算公式为h=δR/( b/ h)(式中δ为视差，R为地面分辨率，(b/ h)为基高比)。利用本文视差图计算的高程平均误差为0.299 34 m，对应的视差误差为0.049 89像素，高于1/20像素(即0.05像素)。

图6　小基高比立体影像数据Fig.6　Small baseline stereo images

图7　本文算法与文献[7]MARC算法实验结果对比Fig.7　Comparison of results between our algorithm and MARC algorithm from Ref.[7]

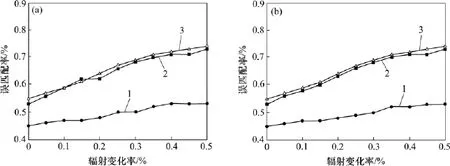
图8　本文算法、文献[7]MARC算法和文献[8]迭代传播算法的量化比较实验结果Fig.8　Statistical results by comparing our algorithm and algorithms from Refs.[7]and[8]

4　结论

1)提出了一种基于模糊逻辑的多尺度小基高比立体匹配方法，该方法利用HSL色彩模式下的模糊逻辑相似性测度函数计算初始成本，提高了算法在辐射差异条件下的鲁棒性。在视差计算过程中，加入了基于十字支撑臂的自适应窗口成本累积策略，提高了视差估计的准确性。

2)在获得整数级视差后，利用基于迭代相位相关的亚像素级匹配方法获得高精度的亚像素级视差，克服了小基高比给深度重建造成的误差。

3)本文提出的小基高比立体匹配方法在辐射差异条件下具有良好的鲁棒性，并且可以获得高精度的亚像素级视差。

[1]SCHARSTEIN D,SZELISKI R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International journal of computer vision,2002,47(1/2/3): 7-42.

[2]SUN X,MEI X,JIAO S,et al.Real-time local stereo via edge-aware disparity propagation[J].Pattern Recognition Letters,2014,49(11):201-206.

[3]ZHANG K,LU J,LAFRUIT G.Cross-based local stereo matchingusingorthogonalintegralimages[J].IEEE Transactions on Circuits and Systems for Video Technology, 2009,19(7):1073-1079.

[4]WANG L,YANG R,GONG M,et al.Real-time stereo using approximatedjointbilateralfilteringanddynamic programming[J].Journal of Real-Time Image Processing, 2014,9(3):447-461.

[5]BESSE F,ROTHER C,FITZGIBBON A,et al.Pmbp: Patchmatchbeliefpropagationfor correspondencefield estimation[J].International Journal of Computer Vision,2014, 110(1):2-13.

[6]WANG H,WU M,ZHANG Y,et al.Effective stereo matching using reliable points based graph cut[C]//Visual Communications and Image Processing.Washington,USA: IEEE Computer Society,2013:1-6.

[7]DELON J,ROUGÉ B.Small baseline stereovision[J].Journal of Mathematical Imaging and Vision,2007,28(3):209-223.

[8]门朝光,边继龙,李香.基于迭代传播的小基高比立体匹配方法[J].中南大学学报(自然科学版),2012,43(4): 1362-1369. MEN Chaoguang,BIAN Jilong,LI Xiang.Iterative diffusion based stereo matching method for small baseline[J].Journal of Central South University(Science and Technology),2012, 43(4):1362-1396.

[9]范大昭,申二华,李禄,等.基于相位相关的小基高比影像匹配方法[J].测绘科学技术学报,2013,30(2):154-157. FAN Dazhao,SHEN Erhua,LI Lu,et al.Small baseline stereo matching method based on phase correlation[J]. Journal of Geomatics Science and Technology,2013,30(2): 154-157.

[10]李禄,范大昭,耿则勋,等.改进相位相关算法的小基高比影像亚像素匹配[J].测绘科学,2014,44(1):183-188. LI Lu,FAN Dazhao,GENG Zexun,et al.Sub-pixel matching for small baseline and height ratio stereo image pairs based on enhancedphasecorrelationalgorithm[J].Scienceof Surveying and Mapping,2014,44(1):183-188.

[11]ITO K,SASAKI M,AOKI T,et al.Generating robust and stabledisparitymapusingphase-basedcorrespondence matching from stereo video sequence[C]//2013 2nd IAPR Asian Conference on Pattern Recognition.Washington,USA: IEEE Computer Society,2013:586-590.

(编辑罗金花)

Multiscale stereo matching method for small baseline based on fuzzy logic

MANing1,2,MEN Yubo1,LI Xiang1,MEN Chaoguang1
(1.College of Computer Science and Technology,Harbin Engineering University,Harbin 150001,China;
2.College of Computer Science and Information Engineering,Harbin Normal University,Harbin 150001,China)

A stereo matching method for small baseline was proposed to solve radiometric variations and depth accuracy in small baseline stereovision.Firstly,the multiscale space was constructed using wavelet transform.The raw matching cost was calculated by fuzzy logic based similarity function and cross based window.Then the“winner takes all”strategy was used to compute integral disparities.Finally,the sub-pixel stereo matching method based on iterative phase correlation was employed to obtain sub-pixel disparities on the basis of integral disparities.The results show that the proposed stereo matching method overcomes the radiometric variations problem and achieves the dense disparity map with sub-pixel precision higher than 1/20.

stereo matching;small baseline;adaptive window;fuzzy logic;sub-pixel disparity

门朝光，博士，教授，博士生导师，从事计算机视觉研究；E-mail:menchaoguang@hrbeu.edu.cn

TP391.4

A

1672-7207(2016)07-2304-07

10.11817/j.issn.1672-7207.2016.07.018

2015-07-03；

2015-09-03

国家自然科学基金资助项目(61100004，11547157)；黑龙江省自然科学基金资助项目(F201320)(Projects(61100004, 11547157)supported by the National Natural Science Foundation of China;Project(F201320)supported by the Natural Science Foundation of Heilongjiang Province)