气辅共挤精密成型中2种方法处理气体层的比较

邓小珍，柳和生，黄益宾，黄兴元，何建涛(1.江西省精密驱动与控制重点实验室 南昌工程学院，江西 南昌，0099；.南昌大学 聚合物加工研究室，江西 南昌，001；.上饶师范学院 物理与电子信息学院，江西 上饶，4001)

气辅共挤精密成型中2种方法处理气体层的比较

邓小珍1,2，柳和生2，黄益宾3，黄兴元2，何建涛2
(1.江西省精密驱动与控制重点实验室 南昌工程学院，江西 南昌，330099；
2.南昌大学 聚合物加工研究室，江西 南昌，330031；
3.上饶师范学院 物理与电子信息学院，江西 上饶，334001)

将共挤口模内气体层分别简化为完全滑移边界条件和不可压缩流体，基于流变学基本方程和Phan-Thien Tanner(PTT)本构方程，建立L型截面三维非等温黏弹性多层气辅精密共挤成型数值模型，并采用稳定的数值求解技术对数值模型进行模拟计算，将2种数值模型模拟计算所得结果进行对比分析。研究结果表明：2种数值模型模拟所得口模内熔体的速度场、压力场、剪切速率、应力场和温度场等分布基本一致，但两者模拟所得口模出口端面熔体的边界和层间界面形貌略有差异，将气体层简化为完全滑移边界条件模拟所得口模出口端面熔体的边界和层间界面形貌更接近实验结果。

气辅共挤；气垫层；不可压缩流体；非等温；数值模拟

气体辅助挤出工艺被BRZOSKOWSKI等[1]应用于橡胶成型，研究结果表明，口模壁面与橡胶熔体表面之间存在的气垫膜层能有效减小橡胶熔体在口模中的流动阻力，有利于提高橡胶制品质量和产量。LIANG等[2]将气体辅助挤出工艺应用于塑料挤出成型过程中，研究结果表明，由于口模内壁与塑料熔体表面之间气垫膜层的润滑作用，使得塑料熔体在口模内的流动由完全黏着的非滑移流动转变为非黏着的完全滑移流动，这能有效减小黏弹熔体的挤出胀大率，提高塑料挤出制品质量。此后，国内外学者对塑料气体辅助挤出和共挤出成型工艺进行了大量的实验和数值模拟研究，研究结果表明，气体辅助挤出工艺有利于减小塑料熔体的离模膨胀[3-5]、偏转变形[6-8]及黏性包围现象[9-10]，能有效提高挤出制品的产量和质量[11]。然而，现有关于气体辅助挤出或共挤出成型工艺的数值模拟研究绝大多数是将气体层简化为完全滑移边界条件。柳和生等[10]将气体层简化为不可压缩流体单独作为1层流动，进一步从理论上明确了气体压力对气辅共挤成型的影响，但对2种方法处理气体层的模拟结果未进行比较和评价。为此，本文作者以L型截面塑料异型材气辅双层共挤成型为例，分别将气体层简化为完全滑移边界条件和不可压缩流体单独作为1层流动，建立三维非等温黏弹性数值模型，对所建模型进行有限元模拟计算，分析比较这2种模型模拟所得口模内流场及口模出口处熔体边界和层间界面形貌的异同，并以实验结果为依据，对气辅共挤成型过程中2种处理气体层的方法进行评价。

1　数值模型及模拟方法

1.1几何模型及网格划分

图1所示为共挤出流道的几何模型及有限元网格图Ⅰ。共挤出流道分入口平流区、收敛流动区、传统共挤区和气辅共挤区4部分，口模收敛角度为10°。采用八节点六面体单元进行网格划分，靠近壁面、界面及口模口处因流场变化较大，网格划分适当加密。

图2所示为共挤出流道的几何模型及有限元网格图Ⅱ，其中t为气体层厚度，本文研究取t=0.1 mm。共挤出流道结构组成及网格划分与图1所示相同。

1.2基本方程及本构方程

针对气辅共挤出成型过程中流体的流动特点和稳定挤出的工艺条件，本文假设成型过程中流体的流动是系统物理量不随时间变化的稳态层流过程，且流体为不可压缩，同时忽略流体重力和惯性力对成型的影响。由此，得气辅共挤成型的流场控制方程如下。

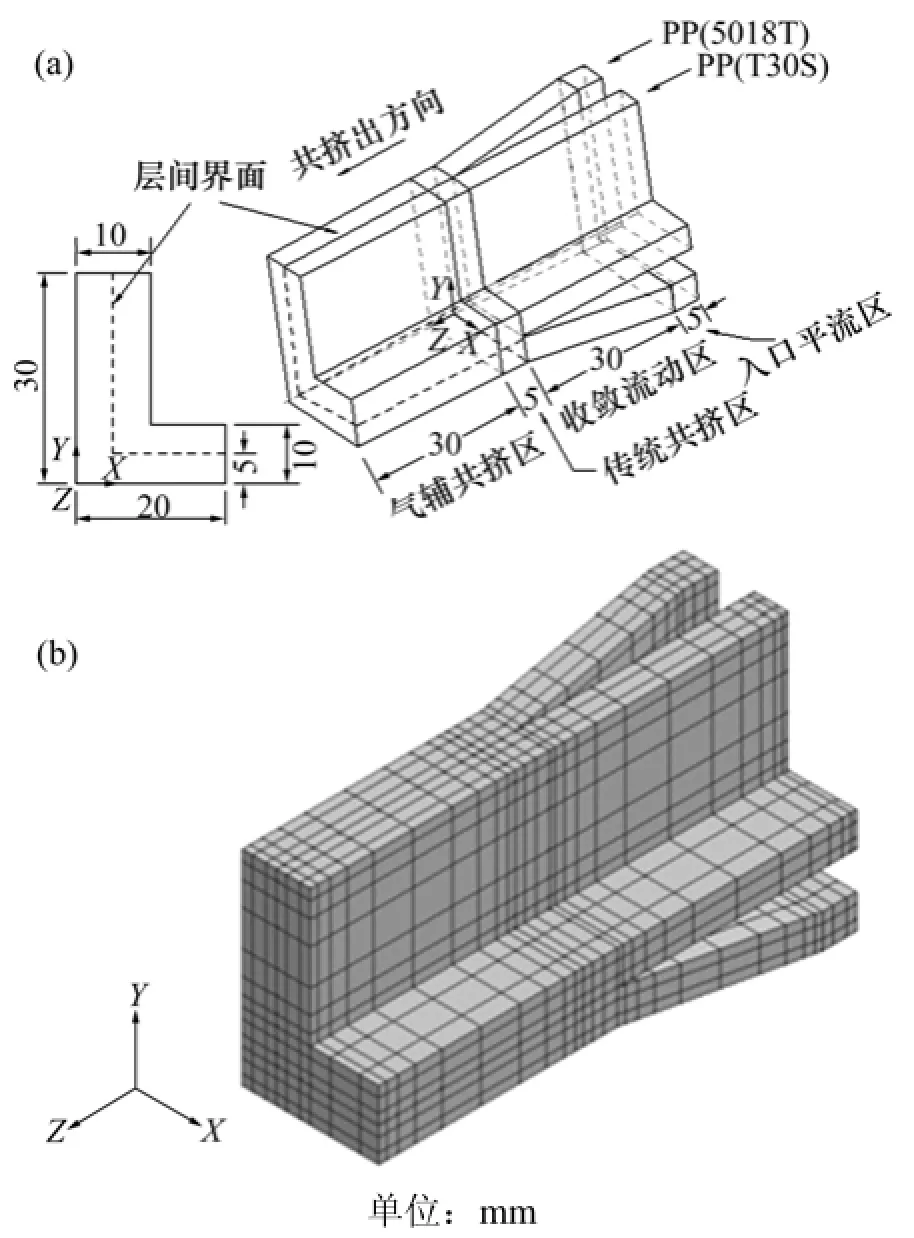
图1　气辅共挤出流道的几何模型及有限元网格图ⅠFig.1　Gas-assisted co-extrusion die geometry and its finite element meshⅠ

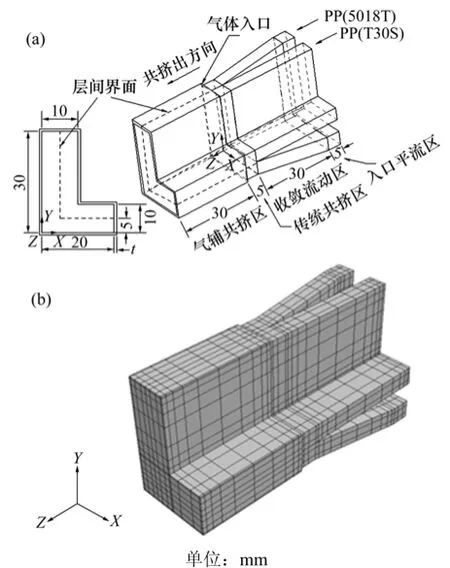
图2　气辅共挤出流道的几何模型及有限元网格图ⅡFig.2　Gas-assisted co-extrusion die geometry and its finite element meshⅡ

连续方程：

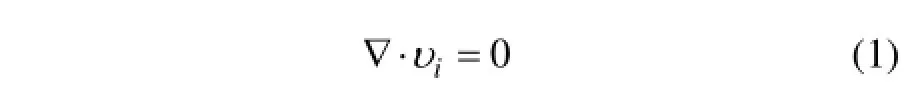
动量方程：

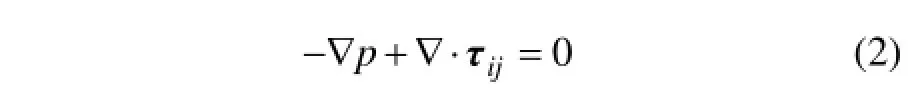
能量方程：

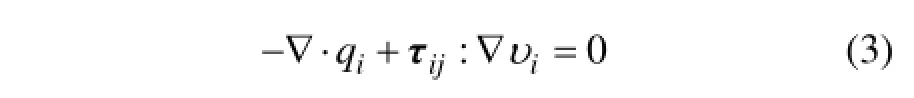
式中：▽为哈密尔顿算子；iυ为速度分量，m/s；p为流体的静压力，Pa；ijτ为剪切应力张量，Pa；q为导热能量，W/m2。

本文采用能较好描述多相塑料熔体在挤出口模内分层流动的PTT本构模型，其表达式为

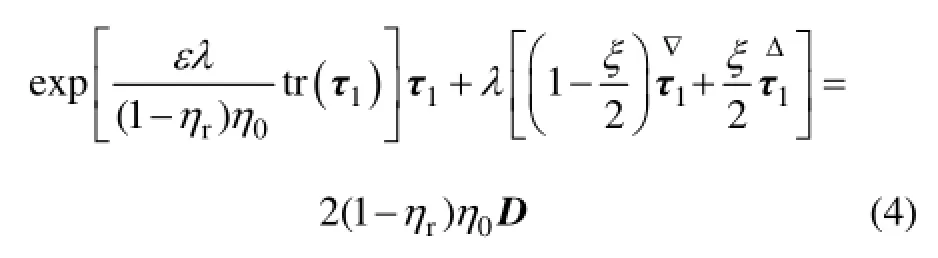
式中：ε是与熔体拉伸特性有关的材料参数；λ为松弛时间，s；rη为黏度比，(其中，1η为熔体零剪切黏度中的黏性分量，0η为熔体零剪切黏度)；ξ是与熔体剪切黏度有关的材料参数；为偏应力张量1τ的上随体导数，为偏应力张量1τ的下随体导数，；D为形变速率张量，。

在非等温条件中，塑料熔体黏度对温度的依赖性，采用Arrhenius方程[12]表示：

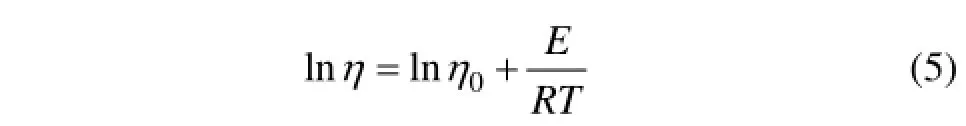
式中：E为材料在恒定剪切速率或恒定剪切应力下的黏流活化能，J/mol；R为气体常数，其值为8.32 J/(mol·K)；T为绝对温度，K。

1.3材料物性参数和边界条件

本文研究用塑料熔体为2种不同牌号的聚丙烯，即PP(T30S)和PP(5018T)，参考文献[13-15]，取PTT本构参数和Arrhenius方程相关参数如表1所示。

口模内气体为190℃的压缩空气，其黏度为常数26.38×10-6Pa·s，热传导系数k为常数0.034 W/(m·K)，恒压比热容Cp为常数1 005 J/(kg·K)。模拟计算时，两聚合物熔体温度均设定为190℃，PP(T30S)熔体流率设置为0.88 cm3/s，PP(5018T)熔体流率设置为1.13 cm3/s。

用υn，υs，fn和fs分别表示边界面上的法向速度、切向速度、法向应力和切向应力，边界条件具体设置如下。

1)流体入口条件。

① 气体入口：设定为压力入口，即fn=xPa，fs=0Pa ，本文设定x=70 kPa。以恒温条件为热力学入口边界条件。

2)共挤壁面条件。

① 将气体层简化为完全滑移边界条件：口模壁面与熔体表面之间形成了稳定的气垫膜层，可视为熔体与口模壁面之间无黏着，熔体呈完全滑移状态挤出，即以fs=0Pa 代替气垫层的作用，壁面速度 υn= 0 m/s。设定壁面为恒温条件。

② 将气体层单独作为1相：设定气体与口模壁面无滑移，即满足 υn=0m/s和 υs=0m/s。设定壁面为恒温条件。

3)流体界面条件。

界面上流体表面张力对成型的影响忽略不计，保持界面两侧应力平衡，即满足动力学条件：(k1，k2=Ⅰ，Ⅱ，Ⅲ)。不考虑界面上流体间的相对滑移，且流体流动没有穿透界面，即满足运动学条件：和n0υ=m/s。界面上温度连续，热通量连续，即满足能量守恒条件：和。上述条件中Ⅰ，Ⅱ和Ⅲ分别表示2种不同的塑料熔体和气体，q为热通量。

表1　材料物性参数Table 1　Material property parameters

4)流体出口条件。

在无外力牵引的条件下，出口面上流体满足：n0f=Pa和s0υ=m/s，温度恒定。

2　模拟结果比较

2.1口模出口端熔体边界和层间界面形貌比较

图3所示为将气辅共挤段的气体层分别简化为完全滑移边界条件和不可压缩流体时模拟计算收敛后的口模出口端面熔体边界和层间界面形貌。

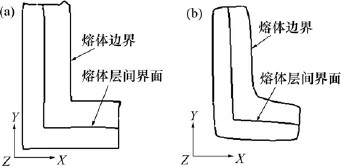
图3　模拟所得口模出口端面熔体边界和层间界面形貌的模拟结果Fig.3　Simulation results of melt boundary and interface profile at the die exit plane

由图3可知：将气体层简化为完全滑移边界条件和不可压缩流体模拟计算得到的口模出口端熔体边界形貌及层间界面形貌略有不同，前者熔体边界直角处以略为不规则的直线段过渡(但L型内直角处较为平直)，且界面夹角略为收紧(即略小于90°)；后者熔体边界直角处以圆滑曲线过渡(L型内直角处更为明显)，且界面夹角略为张开(即略大于90º)。本文实验过程中观察到，气辅共挤成型时，口模出口端熔体边界直角处以平直直角过渡，且界面夹角略为收紧(即略小于90°)，如图4所示。图4中白色熔体为PP(T30S)，黑色熔体为PP(5018T)，与模拟用材料一致。

比较图3和图4可知：对气辅共挤成型过程进行数值模拟时，将稳定的气垫层简化为完全滑移边界条件模拟所得口模出口端熔体的边界形貌和层间界面形貌更接近实验现象。

2.2速度场比较

图5~7所示分别为2种模拟计算收敛后口模出端面上熔体X向、Y向和Z向速度分布。由图5~7可知：2种模拟计算后所得口模出口端面上熔体的X向和Y向速度分布完全一致，且接近0 m/s；2种模拟计算后所得口模出口端面上熔体的Z向速度分布均匀，即两者均呈柱塞状挤出，但将气体简化为不可压缩流体时熔体的Z向速度略大于将气体层简化为完全滑移边界条件时熔体的Z向速度，这是气体流速大于熔体流速，气体对熔体的拖动作用引起。

图4　实验所得口模出口端熔体边界和层间界面形貌的实验结果Fig.4　Experimental results of melt boundary and interface profile at die exit plane

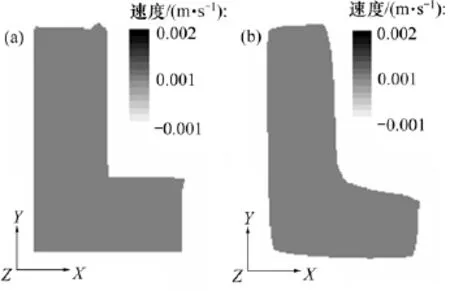
图5　口模出口端熔体X向速度分布Fig.5　Melt X-velocity distributions at die exit plane

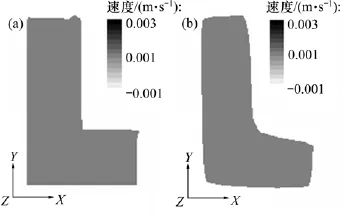
图6　口模出口端熔体Y向速度分布Fig.6　Melt Y-velocity distributions at die exit plane

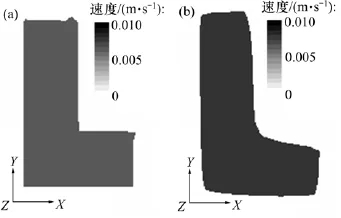
图7　口模出口端熔体Z向速度分布Fig.7　Melt Z-velocity distributions at die exit plane

2.3压力降比较

图8所示为2种模拟计算收敛后，口模内(10，10，0)和(10，10，35)这2点连线上熔体PP(T30S)的压力分布曲线和(0，0，0)和(0，0，35)这2点连线上熔体PP(5018T)的压力分布曲线。

由图8可知：2种条件下模拟得口模内熔体压降均主要集中在气辅共挤段前5 mm的传统共挤区内，30mm的气辅共挤区基本无压降。气体层简化为完全滑移边界条件模拟得PP(T30S)熔体在传统共挤区内的压力由0.032 8 MPa降为0 MPa，PP(5018T)熔体在传统共挤区内的压力由0.063 4 MPa降为0 MPa；气体简化为不可压缩流体模拟得PP(T30S)熔体在传统共挤区内的压力由0.031 5 MPa降为0 MPa，PP(5018T)熔体在传统共挤区内的压力由0.062 9 MPa降为0 MPa。由此，2种条件下模拟所得口模内熔体的压力降基本一致。

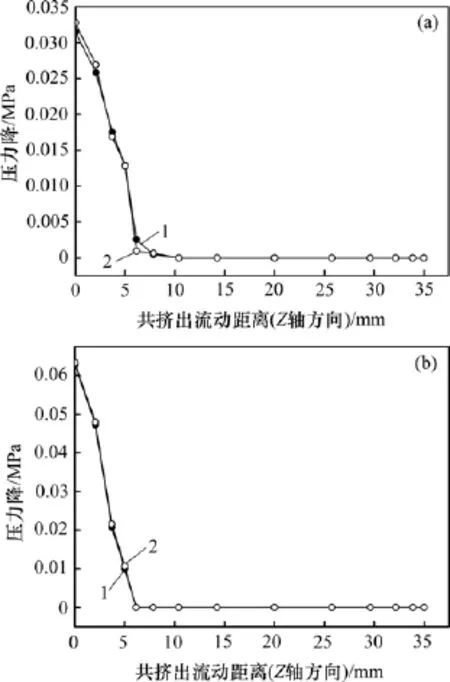
图8　口模内熔体压力分布曲线Fig.8　Melt pressure distributions curve with the die

2.4剪切速率比较

图9所示为2种模拟计算所得口模出口端面上熔体的剪切速率分布，剪切速率表达式为

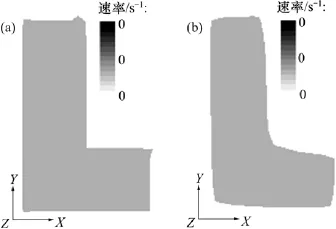
图9　口模出口端熔体剪切速率分布Fig.9　Shear-rate distributions at die exit plane

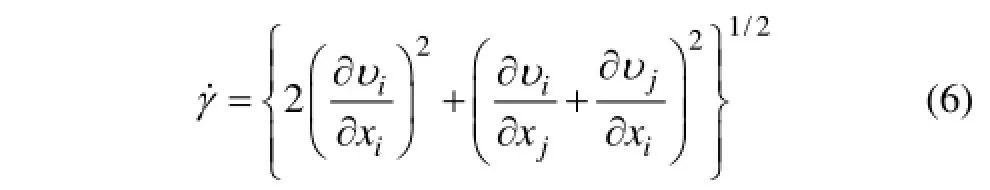
由图9可知：以2种方式处理气体层模拟所得口模出口端面上熔体的剪切速率分布完全一致，即分布均匀且为0 s-1。

2.5应力场比较

图10和图11所示分别为将气体层简化为完全滑移边界条件时模拟(简称“模拟Ⅰ”)所得PP(T30S)和PP(5018T)熔体在传统共挤区和气辅共挤区口模内壁上的应力分布情况。图12和图13所示分别为将气体简化为不可压缩流体时模拟(简称“模拟Ⅱ”)所得PP(T30S)和PP(5018T)熔体在传统共挤区和气辅共挤区口模内壁上的应力分布情况。

由图10~13可知：2种模拟条件下所得PP(T30S) 和PP(5018T)两熔体在传统共挤区和气辅共挤区口模内壁上的应力分布情况和数值基本一致，熔体应力主要集中于5 mm长的传统共挤区内，且法向应力集中于气体入口处，气辅共挤区的应力分布均匀且接近0 Pa。

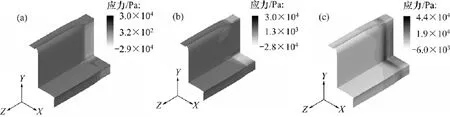
图10　模拟Ⅰ所得熔体PP(T30S)应力分布Fig.10　Stress distributions of melt PP(T30S)for simulationⅠ

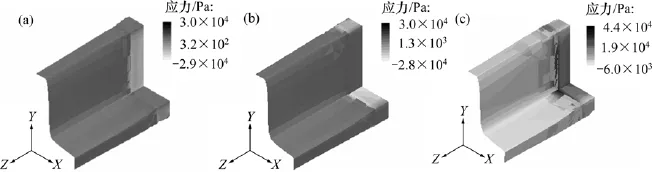
图11　模拟Ⅰ所得熔体PP(5018T)应力分布Fig.11　Stress distributions of melt PP(5018T)for simulationⅠ

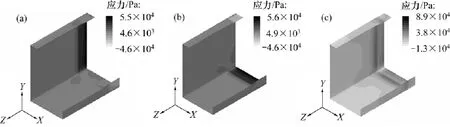
图12　模拟Ⅱ所得熔体PP(T30S)应力分布Fig.12　Stress distributions of melt PP(T30S)for simulationⅡ

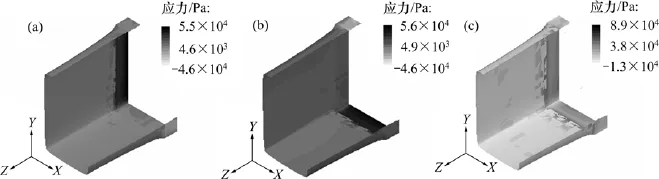
图13　模拟Ⅱ所得熔体PP(5018T)应力分布Fig.13　Stress distributions of melt PP(5018T)for simulationⅡ

2.6温度场比较

图14所示为2种模拟条件下所得熔体在口模内沿共挤出方向(Z轴方向)不同位置横截面上的温度分布情况。

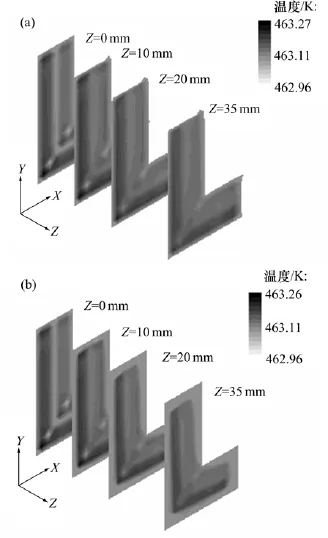
图14　熔体沿共挤出方向的温度分布Fig.14　Temperature distributions along co-extrusion direction

由图14可知：较高黏度熔体PP(5018T)的温度略高于较低黏度熔体PP(T30S)的温度，这是因为聚合物熔体在口模内作剪切流动时的黏性摩擦会产生热效应，引起熔体温度升高，较高黏度的熔体升温大于较低黏度的熔体升温，但由于共挤流道较短，数值计算中设置的熔体流率也较低，故两熔体因黏性摩擦所产生热效应引起的温升并不明显，两熔体在流道内的温度始终保持在190℃左右。此外，由图14还可知：2种条件下模拟所得口模内不同位置横截面上熔体温度分布情况相同，数值也一致。

3　结论

1)气辅共挤成型过程中，分别将气体层简化为完全滑移边界条件和不可压缩流体两种情况时，模拟计算所得口模内熔体的速度场、压力场、剪切速率、应力场和温度场基本一致，但口模出口端面上熔体的边界形貌和层间界面形貌略有不同。

2)将气体简化为完全滑移边界条件时，模拟所得口模出口端面上熔体的边界形貌和层间界面形貌更接近实验结果。

3)将气体简化为不可压缩流体建立的数值模型，可用于研究气辅共挤过程中气体工艺参数对共挤成型的影响，采用将气体简化为完全滑移边界条件建立的数值模型则更为可靠。

[1]BRZOSKOWSKI R,WHITE J L,SZYDLOWSKI W,et al. Air-lubricated die for extrusion of rubber compounds[J].Rubber Chemistry&Technology,1987,60(5):945-956.

[2]LIANG R F,MACKLEY M R.The gas-assisted extrusion of molten polyethylene[J].Journal of Rheology,2001,45(1): 211-226.

[3]黄兴元,柳和生,周国发,等.气体辅助挤出中影响气垫形成及稳定性因素分析[J].塑性工程学报,2005,12(5):101-104, 109. HUANG Xingyuan,LIU Hesheng,ZHOU Guofa,et al.The influence factors on the set up and stability of gas layer in gas assisted polymer extrusion[J].Journal of Plasticity Engineering, 2005,12(5):101-104,109.

[4]柳和生,卢臣,黄兴元,等.T型异型材气辅口模挤出胀大的数值模拟和实验研究[J].塑性工程学报,2008,15(1):158-161. LIU Hesheng,LU Chen,HUANG Xingyuan,et al.Numerical simulation and experimental study on die swell of T-shaped plastic profile extrusion from a gas-assisted die[J].Journal of Plasticity Engineering,2008,15(1):158-161.

[5]肖建华,柳和生,黄兴元,等.气辅挤出胀大比与滑移段长度的关系[J].高分子材料科学与工程,2009,25(7):166-169,174. XIAO Jianhua,LIU Hesheng,HUANG Xingyuan,et al.The relationship between extrudate swell ratio and the length of slip part in gas-assisted extrusion[J].Polymer Materials Science and Engineering,2009,25(7):166-169,174.

[6]黄益宾,柳和生,黄兴元,等.聚合物气辅共挤成型界面的有限元模拟和分析[J].高分子材料科学与工程,2012,28(12): 187-190. HUANG Yibin,LIU Hesheng,HUANG Xingyuan,et al.Finite element simulation and analysis of the gas-assisted co-extrusion interfaceofpolymer[J].PolymerMaterialsScienceand Engineering,2012,28(12):187-190.

[7]邓小珍,柳和生,黄益宾,等.气辅共挤出界面位置对挤出胀大的影响[J].高分子材料科学与工程,2013,29(9):114-118. DENG Xiaozhen,LIU Hesheng,HUANG Yibin,et al.Influence of interface position on die swell in gas-assisted co-extrusion moldingprocesses[J].PolymerMaterialsScienceand Engineering,2013,29(9):114-118.

[8]周文彦,周国发.聚合物多层气辅共挤精密成型机制的数值分析[J].复合材料学报,2009,26(3):90-98. ZHOU Wenyan,ZHOU Guofa.Numerical investigation on the mechanism of polymer multilayer gas assisted co-extrusion precision molding process[J].Acta Materiae Compositae Sinica, 2009,26(3):90-98.

[9]LIU Hesheng,DENG Xiaozhen,HUANG Yibin,et al.Threedimensional viscoelastic simulation of the effect of wall slip on encapsulation in the coextrusion process[J].Journal of Polymer Engineering,2013,33(7):625-632.

[10]柳和生,邓小珍,黄益宾,等.气体压力对气辅共挤成型界面的影响[J].高分子材料科学与工程,2014,30(3):119-123. LIU Hesheng,DENG Xiaozhen,HUANG Yibin,et al.Effect of air pressure on interface profile in gas-assisted coextrusion process[J].Polymer Materials Science and Engineering,2014, 30(3):119-123.

[11]ARDA D R,MACKLEY M R.Sharkskin instabilities and the effect of slip from gas-assisted extrusion[J].Rheologica Acta, 2005,44(4):352-359.

[12]徐佩弦.高聚物流变学及其应用[M].北京:化学工业出版社, 2003:59-60. XU Peixian.Polymer rheology and its application[M].Beijing: Chemical Industry Press,2003:59-60.

[13]TAKASE M,KIHARA S,FUNATSU K.Three-dimensional viscoelastic numerical analysis of the encapsulation phenomena in coextrusion[J].Rheologica Acta.1998,37(6):624-634.

[14]SUNWOO K B,PARK S J,LEE S J,et al.Numerical simulation of three-dimensional viscoelastic flow using the open boundary conditionmethodincoextrusionprocess[J].Journalof Non-Newtonian Fluid Mechanics.2001,99(2):125-144.

[15]SUNWOO K B,PARK S J,LEE S J,et al.Three-dimensional viscoelastic simulation of coextrusion process:comparison with experimental data[J].RheologicaActa.2002,44(1/2):144-153.

(编辑罗金花)

Comparison of two methods for gas layer in gas-assisted precision co-extrusion molding

DENG Xiaozhen1,2,LIU Hesheng2,HUANG Yibin3,HUANG Xingyuan2,HE Jiantao2
(1.Jiangxi Province Key Laboratory of Precision Drive and Control,Nanchang Institute of Technology, Nanchang 330099,China;
2.Polymer Processing Research Laboratory,Nanchang University,Nanchang 330031,China;
3.School of Physics and Electronic Information,Shangrao Normal University,Shangrao 334001,China)

Three-dimensional non-isothermal mathematical models were established for two-layer gas-assisted precision co-extrusion through a L-shaped channel based on the gas layer simplified as the full-slip boundary condition or the incompressible fluid.The Phan-Thien and Tanner(PTT)model was considered as viscoelastic constitutive equations.The numerical simulations were presented using the finite element method and the results were compared and analyzed.The results show that velocity,pressure,shear-rate,stress and temperature distribution of making gas layer as the full-slip boundary condition coincide with those of making gas layer as the incompressible fluid,but the melt boundary and interface profile are different at the die exit.By comparing the simulation results with experimental ones,it is shown that the former is more reliable.

gas-assisted co-extrusion;gas layer;incompressible fluid;non-isothermal;numerical simulation

柳和生，博士，教授，博士生导师，从事高分子材料成型与加工研究；E-mail:hsliu@vip.163.com

TQ320.66

A

1672-7207(2016)07-2227-08

10.11817/j.issn.1672-7207.2016.07.007

2015-07-13；

2015-09-13

国家自然科学基金资助项目(51163011)；江西省青年科学基金资助项目(20122BAB216012)(Project(51163031)supported by the National Natural Science Foundation of China;Project(20122BAB216012)supported by the Natural Science Foundation of Jiangxi Province of China)