基于先进交通信息的多目标多类用户降级路网双层优化

曾明华，杨晓光，李夏苗(1.华东交通大学 轨道交通学院，江西 南昌，001；.同济大学 交通运输工程学院，上海，01804；.中南大学 运输工程学院，湖南 长沙，410075)

基于先进交通信息的多目标多类用户降级路网双层优化

曾明华1,2，杨晓光2，李夏苗3
(1.华东交通大学 轨道交通学院，江西 南昌，330013；
2.同济大学 交通运输工程学院，上海，201804；
3.中南大学 运输工程学院，湖南 长沙，410075)

考虑先进的出行者信息系统(ATIS)与可变信息板(VMS)的共同影响，研究混合交通(普通交通与突增的应急交通)在降级路网中的随机均衡分配及路网的性能优化。利用应急交通可靠度和路段负效用2个目标定义广义路径费用，并基于VMS信息效用与路段广义费用设计了新的路径长度(path size，PS)属性公式，进而构造改进的路径长度logit(PSL)模型；建立以降级路段的最差容量利用系数为优化变量的多类用户多目标双层规划模型，其中，下层是基于PSL模型的混合交通随机用户均衡分配模型。利用应急交通的可靠度定义适应度函数，设计以进化算法为主体框架的优化算法，通过求解获得流量分布、ATIS占有率与服从率以及各项性能指标。研究结果表明：模型与算法是可行有效；相对于随机模拟，优化可以大幅度提升应急交通的可靠性，VMS能辅助ATIS以提升应急交通可靠性并降低全路网的总期望出行时间费用；需求增长对降级路网性能会产生较大影响，但VMS仍能在需求增长时有效优化系统性能。

交通工程；降级路网双层优化；改进路径长度logit模型；应急疏散；先进交通信息

大型市民活动、体育赛事以及突发灾害等往往会造成局部区域交通需求激增的交通事件。若不对城市交通网络进行提前优化与规划进行预案，则可能造成交通拥堵甚至大面积长时间交通状况恶化。交通事件易造成交通拥堵或交通事故，常用应急疏散问题来处理，包括应急疏散优化与路径规划等，如基于动态交通分配[1]、鲁棒优化[2]等疏散优化，基于车道建模的应急疏散路径规划[3-4]。交通需求不确定是应急交通疏散中面临的主要问题之一，杨兆升等[5-6]采用多目标和双层规划分别研究了需求不确定和应急状态下的优化问题。鲁棒优化是解决交通需求不确定的有用工具。YAO等[2]基于鲁棒优化方法提出了应急疏散的鲁棒线性规划模型。鲁棒优化主要研究不确定性对系统的影响以设计性能最优的新系统。针对小区之间的交通需求很难准确预测，孙华等[7]假定起讫点(OD)需求不确定且属于有界区间，利用鲁棒优化的方法建立考虑用户均衡约束的交通网络设计极小极大模型，表明可得到更高可靠性网络。交通事件发生时局部交通需求波动会导致部分路段容量下降。DU等[8]分析了降级路网出行者路径选择行为并提出降级交通系统的理论框架，黎茂盛等[9]分析了出行者对降级路网的认知与交通流均衡分析模型。短期的路网容量降级会影响路网出行时间可靠性等系统性能，对路网可靠性的研究主要集中在连通可靠性、出行时间可靠性和容量可靠性[10]，基于出行时间的可靠性测度主要有出行时间可靠性[11-12]、出行时间预算可靠性[13-15]，也有利用期望总时间[16]表达可靠性概念。况爱武等[12]研究考虑OD对出行时间可靠性的道路网容量可靠性。SZETO 等[15]基于可靠性研究带容量约束随机公交分配行为。LO等[13]提出用户出行时间预算可靠性并研究多类用户降级路网混合均衡及网络设计。要甲等[17-18]基于降级路网出行时间预算可靠性分别研究小汽车和地铁之间不存在和存在换乘的多模式交通平衡问题。SUMALEE等[19]提出部分用户认识到路网降级的部分用户平衡概念与模型，蒲云等[16]研究基于部分随机用户平衡(SUE)的可靠性网络设计。无论是所有路段各取不同降级系数[13]，还是各路段取统一降级系数[17-18]，都难以反映实际情况，不适用于应急疏散时获取部分路段的最优降级系数以达到系统最优，并且以往研究没有或很少在降级路网研究中挖掘先进出行者信息系统(ATIS)与可变信息板(VMS)对用户出行行为的影响。为此，本文作者针对应急疏散交通网络系统的多目标、多用户、主从博弈、路径选择随机性、信息化等现实特征，研究ATIS与VMS影响下基于降级路网多目标多类用户混合交通均衡的应急疏散双层优化问题，结合路径长度logit(PSL)模型建立基于可靠度和负效用双准则的多目标多类用户双层规划模型，并设计基于进化算法与随机交通分配算法的求解算法。

1　基本问题描述

将交通网络描述为G=(V, E)，其中，V为节点集合，E为区域所有路段集合。记W={w}为OD对集合，Rw为w∈W之间的路径集合。设 va为路段a∈E的交通流量，为相应向量，R+为非负实数集；为路径OD对w间上的交通流量，记为路径流量向量。交通事件发生时，设应急疏散OD为，对应路径集合为 Rwˊ，交通事件源的应急需求为 qwˊ或。假设交通系统中应急交通全部配置ATIS而普通交通部分配置ATIS系统，从而，将用户分为3类，第1类有ATIS且服从诱导指令，第2类有ATIS但不服从指令，第3类无ATIS。3类用户的相关变量如路段出行时间，路段与路径流量、路径选择概率以及OD对间的交通需求量等分别在相应变量的右下角用1，2和3标示。ATIS 和VMS通过发布信息影响多类出行者的随机路径选择行为，从而导致混合交通随机均衡，事故路段交通需求突增导致其上出行负效用大幅提升进而使路网部分路段容量降级至最差容量利用系数(WCUF)，通过调整该系数追求应急疏散交通的最大可靠度并保证较小的期望出行时间。

2　容量降级路网出行时间可靠性与广义路径费用

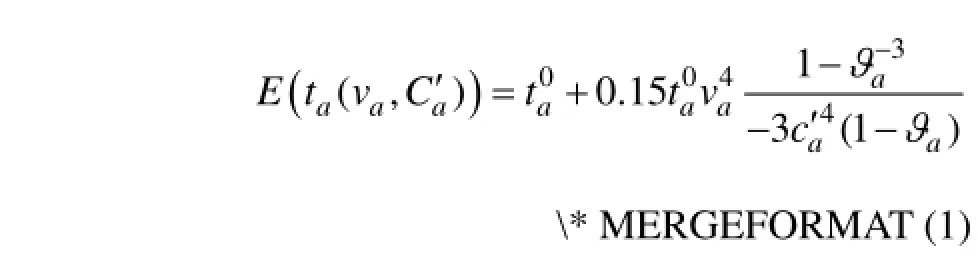
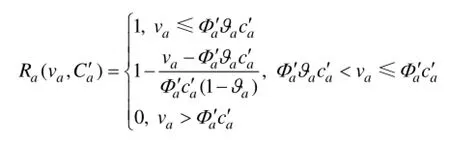
3　改进路径长度logit模型及多类用户需求计量

3.1随机路径选择PSL基本模型

ATIS和VMS所提供的实时交通信息只能在一定程度上提升出行的确定性，不能消除交通系统随机性，假设各类用户对广义路径费用的感知误差独立同Gumbel分布，用户出行遵循某种随机程度(用正参数θ表示)的路径选择。采用由Ben-Akiva提出的PSL模型[20]，该模型区别于多项式logit模型在指数部分增加了1项PS属性项，既能克服C-logit的理论缺陷，又相对简单且具有交叉巢式logit模型刻画重叠路径的能力。设μ是待定参数(取μ=1)，为PS属性，则PSL模型如下：

3.2一种新的PS属性计算途径

PS属性的原始公式为[20]其中：La与Lr分别为路段a和路径r的“长度”；Er为OD对w之间的路径r上的路段集合。

在以往的研究中，该PS属性的计算通常只用到物理长度、出行时间、出行费用等，未见将VMS信息对路网及交通流的局部影响用来计算PS属性的相关报道。交通事件期间，事发路段的交通流突然增大，导致部分路段容量下降。为合理管控拥堵并防止交通事故，在事发路段前端或其他重要路段上游部分设置VMS，为司机提供该路段及容量下降路段的实时信息。利用VMS信息效用的衰减特性来描叙VMS对其所处路段及其影响范围内路段的影响系数，并与路段广义费用共同定义PS属性中的路段“长度”，进而构造一种新的PS属性公式。

采用信息效用的衰减因子来描叙VMS信息效用对其后续路段产生的影响随距离增长而减弱的特征。路径r上VMS的有效影响路段指路径r上设置VMS所在路段a的后续路段。若某路径上设置了几个VMS装置，则VMS的独立影响路段集合指路径r上路段a中VMS的有效影响路段集合中删除下个VMS的有效影响路段后的剩余路段，且满足(δ为常数)。设k为路径r上路段a之后的第n条路段，路段k的信息在路段a上VMS中显示时，信息效用的衰减因子记为。可取，与信息精度及出行者对信息信任度成正相关，也可取，其中，η为常数。综合幂函数与指数函数表示方法，将信息效用的衰减因子表示为。

设kψ表征路段k的交通信息量，因服务水平直接反映了道路的典型特征信息以及发生交通事故的可能性和拥堵频率，故采用路段流量容量比表示交通信息量，令。于是，定义VMS对路径r下游路段的影响系数为

其中：az表示路段a是否设置VMS的哑变量。从而，将路段a上VMS对路径r中车流的影响系数表示为

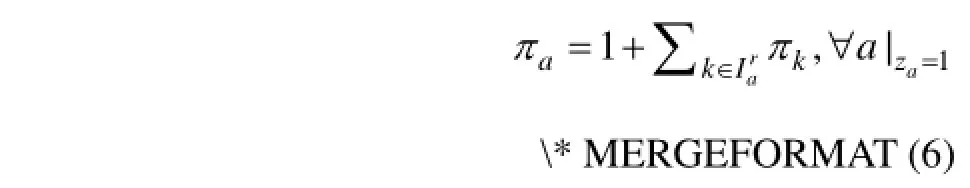
式表明：(后续)路段通过能力使用率越低，影响系数越大，VMS的效用越大；β越大，衰减因子越小，VMS的效用越大。

设路段a的“长度”La定义如下。

1)设置了VMS信息的路段“长度”为

2)由于VMS显示了其后续路段的重要交通信息，这些信息会影响出行者选择路段a的没有设置VMS的后续路段，所以定义这些路段“长度”为

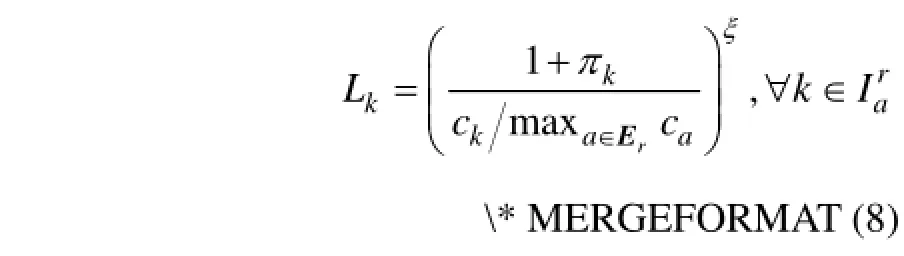
3)对其他所有没有设置VMS的路段，令

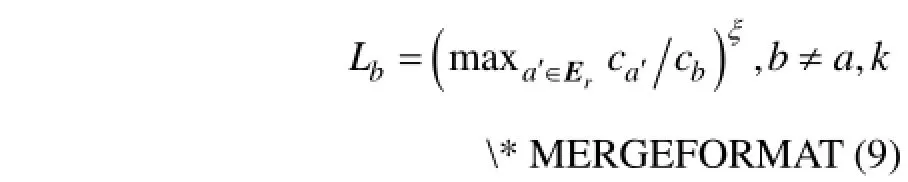
其中：ξ∈(0,1]是调节VMS信息与路段费用之间相对影响的参数。路段a，k，b的“长度”满足Lb，这是因为。路径“长度”为。

式~定义的路段“长度”结合了路段广义费用与VMS信息效用，它通过VMS信息捕捉局域范围内路径间的相似性。路段a的重叠次数越少，或者路段“长度”越长，则PS属性值越大；若路段a的影响系数越大或广义费用越低，则路段“长度”越长。PS属性值越大，则其选择概率越大。

3.3ATIS影响下多类用户需求计量

ATIS市场占有率常常内生地表示为信息收益即有无ATIS两大类用户广义费用之差的函数[22]，假设OD对w上的普通交通的ATIS市场占有率为，则

4　应急疏散降级路网的随机用户均衡双层规划模型与算法

4.1随机用户均衡双层规划模型设交通事件所在路段为Ia∈E；且假设局部交通需求剧增致使该路段容量急剧下降，即，为较小正数。设为服务水平阈值，按选择容量降级路段，0。按下式计算应急疏散OD对的行程时间可靠性：

下层多目标数学规划模型实现 qw和在部分路段随机降级的路网中的PSL随机均衡分配

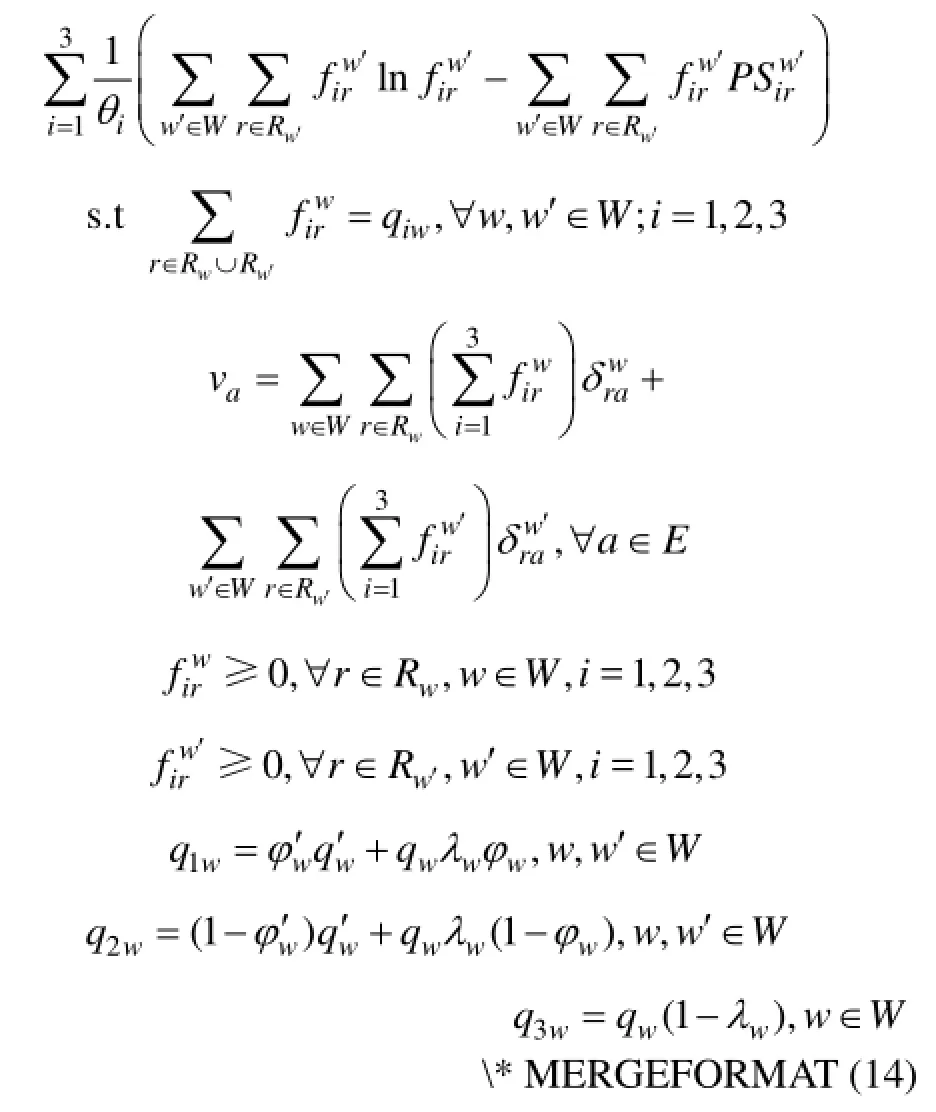
其中：分散参数1θ＞2θ＞3θ反映事件期间3类出行者对路网和交通的熟悉程度；和为利用ATIS市场占有率与服从率等宏观变量计算得到的各类用户需求量。

4.2双层规划的进化算法

利用进化算法与随机用户均衡(SUE)分配算法求解上述双层规划模型。

1)进化算法求解上层规划的具体步骤如下：

Step 5收敛判断。若达到最大迭代次数，则退出，否则，置并转Step 1；

2)结合PSL随机用户平衡分配及ATIS占有率和服从率计算来求解下层规划的步骤如下：

Step 2调用一次混合交通PSL-SUE算法：

Step 2.4 SUE收敛判断。若满足终止条件：

5　算例分析

算例网络采用Nguyen&Dupuis网络，共有13顶点，19边，25条路径，4个普通交通OD对(1,2)，(1,3)，(4,2)和(4,3)，1个应急交通OD对(5,3)。普通交通OD需求矩阵为对称阵，且。普通交通OD需求为(单位为辆)，应急交通OD需求为辆。路段部分特征如表1所示。VMS设置在路段(5,6)与(5,9)上。

按普通交通需求q0=[960, 800; 800, 960]时，优化计算得到应急交通可靠性为1；当普通交通OD矩阵取[1 440, 1 200; 1 440, 1 200]时，优化计算得到应急交通可靠性为0。因此，选取介于这2个OD矩阵之间的不同需求水平：

q1=[1 020, 850; 850, 1 020]；

q2=[1 080, 900; 900, 1 080]；

q3=[1 140, 950; 950, 1 140]；

q4=[1 200, 1 000; 1 000, 1 200]；

q5=[1 260, 1 050; 1 050, 1 260]；

q6=[1 320, 1 100; 1 100, 1 320]；

q7=[1 380, 1 150; 1 150, 1 380]。

ATIS占有率和服从率的2种计算方式：CaseA，直接取定ATIS的市场占有率与服从率；Case B，内生地确定普通交通的ATIS市场占有率和服从率。

所有计算都能很好地收敛，按普通交通需求q4以Case B处理ATIS计算无VMS信息时的降级路网优化，每10代取1个适应值，其收敛过程如图2所示。

1)直接取定容量下降路段的最差容量利用系数(WCUF)，例如取路段或者，按CaseA对OD需求q4进行随机均衡分配，计算结果都劣于通过优化算法所得，如表2所示。通过大量模拟，按均匀分布随机抽取1 000次路段(5,9)与(9,11)的WCUF，所得结果也比优化算法差。

图1　实例网络Fig.1　Example network

表1　路段特征Table 1　Link characteristics

图2　适应值变化趋势Fig.2　Evolutionary trends of fitness values

2)无论是否考虑降级，Case A和Case B的计算结果(指可靠性、各类总期望出行时间费用(TETTC)以及全路网流量分布及应急交通流量分布)一致，如表3所示。

3)比较不同需求水平情况。

对CaseA，计算得到WCUF变量值及流量分布、TETTC以及平均期望出行时间费用(AETTC)，如表4至表5及图3~6所示。经比较发现：

表2　直接取定WCUF的计算结果比较Table 2　Comparison of calculation results for fixed WCUFs

表3　降级与信息的各种组合下CaseA和Case B的计算结果比较Table 3　Comparison of calculation results for CaseAand B under various combinations of degradation and information

表4　ATIS作用下最优变量及性能指标值Table 4　Optimal variable values and performance indicators consideringATIS

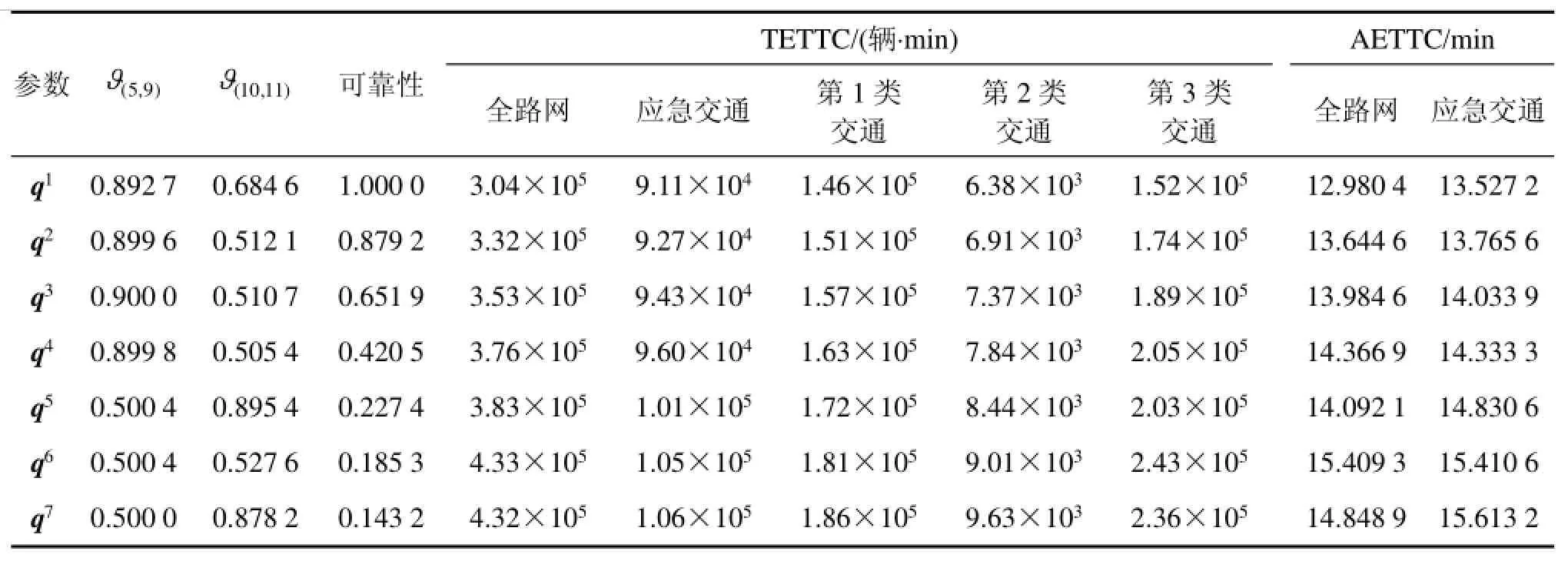
表5　ATIS与VMS作用下最优变量及性能指标值Table 5　Optimal variable values and performance indicators consideringATIS and VMS

① 对任意特定需求，交通系统设置VMS时各项费用变小；当普通交通需求增长时，全路网和第3类交通的TETTC增长最大，第1类交通次之，应急交通再次，第2类交通变化极小；应急交通的AETTC随需求增长而增长，但有VMS参与能使其边际增长率更小。

图3　应急交通可靠性与普通交通需求的关系Fig.3　Relationship between evacuation reliabilities and normal traffic demands

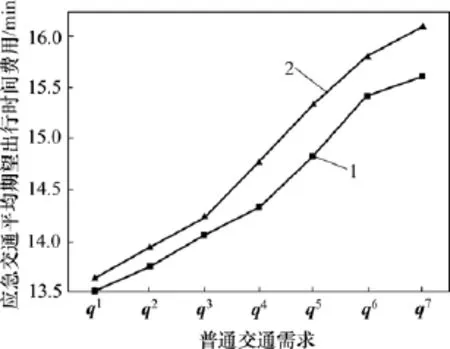
图4　应急交通AETTC与普通交通需求的关系Fig.4　Relationship between evacuation’sAETTC and normal traffic demands

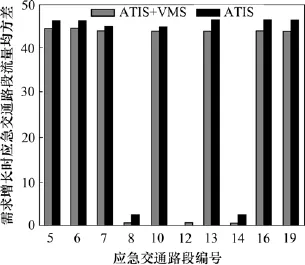
图5　需求增长过程中应急交通各路段流量均方差Fig.5　Mean square error of evacuation traffic on each link when demand increased

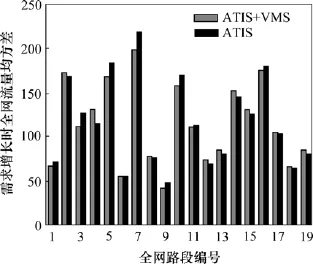
图6　需求增长过程中全路网各路段流量均方差Fig.6　Mean square error of hybrid traffic on network-wide link when demand increased

② 应急交通可靠性随需求增长而下降，且VMS 与ATIS共同作用的应急交通可靠性比只有ATIS的大，且需求较小时VMS对提高可靠性的作用更大。

③VMS与ATIS共同作用下在需求增长时应急交通路段流量均方差比ATIS单独作用时小一些；但对全路网所有交通路段流量均方差并无此现象，这是由于双层规划模型主要针对应急交通进行优化。

6　结论

1)建立了基于路径长度logit随机路径选择模型和面向应急交通可靠度最大化的多目标多类用户双层规划模型，并设计了以进化算法和随机均衡分配算法为基础的降级路网优化算法。

2)采用内生或外生方式，发现普通交通的ATIS占有率和服从率对路网优化结果没有影响。

3)需求增长对系统性能有显著影响，会降低应急交通的可靠度和提高应急交通平均期望出行时间。

4)VMS信息能在ATIS基础上进一步显著提升应急交通可靠度但随需求增长提升度下降，并且能进一步降低应急交通平均期望出行时间且随需求增长降低幅度更大，全路网流量分布和应急交通流量分布随需求变化更小。

[1]陈岳明,萧德云.基于动态交通分配的路网应急疏散模型[J].清华大学学报(自然科学版),2009,49(8):1102-1105. CHEN Yueming,XIAO Deyun.Dynamic traffic assignmentbasedmethodforreal-timetrafficmanagementduring emergencyevacuation[J].JournalofQinghuaUniversity (Science and Technology),2009,49(8):1102-1105.

[2]YAOT,MANDALASR,CHUNGBD.Evacuation transportation planning under uncertainty:a robust optimization approach[J].Network Spatial Economic,2009,9(2):171-189.

[3]王健,胡晓伟,佟晶晶,等.基于车道建模的区域应急疏散路径规划[J].交通运输工程学报,2010,10(2):82-87. WANG Jian,HU Xiaowei,TONG Jingjing,et al.Route planing of regional emergency evacuation based on lane modeling[J]. Journal of Traffic and Transportation Engineering,2010,10(2): 82-87.

[4]XIE C,TURNQUIST M A.Lane-based evacuation network optimization:an integrated lagrangian relaxation and tabu search approach[J].TransportationResearchPartC:Emerging Technologies,2011,19(1):40-63.

[5]杨兆升,宋淑敏,杜鹏程,等.大型公共场所应急状态下交通诱导疏散模型[J].吉林大学学报(工学版),2012,42(3): 588-593. YANG Zhaosheng,SONG Shumin,DU Pengcheng,et al.Traffic guidance evacuation model under the emergency state in public place[J].JournalofJilinUniversity(Engineeringand Technology Edition),2012,42(3):588-593.

[6]杨明,苏标,孙志杰,等.随机OD需求下的多目标离散交通网络设计模型与算法[J].西南交通大学学报,2014,49(1): 119-125. YANG Ming,SU Biao,SUN Zhijie,et al.Model and algorithm of multi-objective discrete transportation network design under stochastic demand among OD pairs[J].Journal of Southwest Jiaotong University,2014,49(1):119-125.

[7]孙华,高自友,龙建成.不确定OD需求下连续交通网络设计的鲁棒优化模型[J].交通运输系统工程与信息,2011,11(2): 70-76. SUN Hua,GAO Ziyou,LONG Jiancheng.The robust model of continuous transportation network design problem with demand uncertainty[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(2):70-76.

[8]DU Z P,NICHOLSON A.Degradable transportation systems: sensitivity and reliability analysis[J].Transportation Research Part B:Methodological,1997,31(3):225-237.

[9]黎茂盛,王炜,史峰.降级路网的认知与交通流均衡分析模型[J].中国公路学报,2006,19(6):87-91. LI Maosheng,WANG Wei,SHI Feng.Cognition of degraded road network and equilibrium analysis model on traffic flow[J]. China Journal of Highway and Transport,2006,19(6):87-91.

[10]WANG D H,QI H S,XU C.Reviewing traffic reliability research[J].Journal of Transportation Systems Engineering and Information Technology,2010,10(5):12-21.

[11]LO H K,TUNG Y K.Network with degradable links:capacity analysisanddesign[J].TransportationResearchPartB: Methodological,2003,37(4):345-363.

[12]况爱武,黄中祥,唐志强.考虑OD对出行时间可靠性的道路网容量可靠性[J].系统工程,2013,31(1):116-120. KUANG Aiwu,HUANG Zhongxiang,TANG Zhiqiang.Road network capacity reliability considering OD pair travel time reliability[J].Systems Engineering,2013,31(1):116-120.

[13]LO H K,LUO X W,SIU B W Y.Degradable transport network: traveltimebudgetoftravelerswithheterogeneousrisk aversion[J].Transportation Research Part B:Methodological, 2006,40(9):792-806.

[14]CHEN A,KASIKITWIWAT P,YANG C.Alternate capacity reliability measures for transportation networks[J].Journal of Advanced Transportation,2013,47(1):79-104.

[15]SZETO W Y,JIANG Y,WONG K I,et al.Reliability-based stochastictransitassignmentwithcapacityconstraints: formulation and solution method[J].Transportation Research Part C,2013,35(9):286-304.

[16]蒲云,刘海旭.基于部分随机用户平衡的可靠性网络设计[J].西南交通大学学报,2011,46(2):321-325. PU Yun,LIU Haixu.Reliable network design based on partial stochastic user equilibrium[J].Journal of Southwest Jiaotong University,2011,46(2):321-325.

[17]要甲,史峰,周钊,等.基于出行时间预算的多模式多类用户城市交通均衡分析[J].中南大学学报(自然科学版),2011, 42(11):3572-3577. YAO Jia,SHI Feng,ZHOU Zhao,et al.Multi-mode and multi-class user's urban transportation euilibrium analysis based on travel time budget[J].Journal of Central South University (Science and Technology),2011,42(11):3572-3577.

[18]孟梦,邵春福,曾靖静,等.降级路网组合出行交通流分配模型与算法[J].中南大学学报(自然科学版),2014,45(2): 643-650. MENG Meng,SHAO Chunfu,ZENG Jingjing,et al.Traffic assignment model and algorithm with combined modes in a degradable transportation network[J].Journal of Central South University(Science and Technology),2014,45(2):643-650.

[19]SUMALEE A,WATLING D P.Travel time reliability in a networkwithdependentlinkmodesandpartialdriver response[J].JournaloftheEasternAsiaSocietyfor Transportation Studies,2003,5:1687-1701.

[20]HALL R W.Handbook of transportation science[M].Berlin, Germany:Springer,1999:5-33.

[21]YIN Y,YANG H.Simultaneous determination of the equilibrium market penetration and compliance rate of advanced traveler information systems[J].Transportation Research Part A:Policy and Practice,2003,37(2):165-181.

[22]YANG H.Multiple equilibrium behaviors and advanced traveler information systems with endogenous market penetration[J]. Transportation Research Part B:Methodological,1998,32(3): 205-218.

(编辑罗金花)

Multi-user and multi-objective bi-level optimization of degradable road network based on advanced traffic information

ZENG Minghua1,2,YANG Xiaoguang1,LI Xiamiao3
(1.School of Railway Tracks and Transportation,East China Jiao Tong University,Nanchang 330013,China;
2.School of Transportation Engineering,Tongji University,Shanghai 201804,China;
3.School of Traffic and Transportation Engineering,Central South University,Changsha 410075,China)

Under the combined effect of advanced traveler information system(ATIS)and variable message sign(VMS), road network performance optimization and stochastic equilibrium behavior of hybrid traffic(including general traffic and emergency demand increased suddenly)were investigated.Generalized path cost was defined by evacuation reliability and link disutility and a new formula for PS attribute was introduced by incorporating VMS information utility and generalized link cost into the prime formula.Furthermore,an adjusted path size logit(PSL)route choice model was proposed.This led to the establishment of a multi-objective multi-user bi-level programming model with west capacity utilization coefficients of degradable link as optimization variables,in which the lower level was constructed to complete stochastic user equilibrium assignment for hybrid traffic based on the PSL model.For the model,optimization algorithmsbased on evolutionary algorithm was formulated using evacuation reliability to define fitness function.Flow distribution, ATIS penetration rate and compliance rate,and several road network performance values were obtained by the proposed solution algorithms.Computations and analyses show that the models and algorithms are feasible and effective.The optimization approach can dramatically enhance evacuation reliabilities compared with stochastic simulation.VMS information can assist ATIS to improve evacuation reliability and decrease the total expected travel time.Demand growth has considerable impacts on degradable road network performance;however,VMS can still obviously optimize system performance.

traffic engineering;bi-level optimization for degradable road network;adjusted path size logit model; emergency evacuation;advanced traffic information

杨晓光，博士，教授，博士生导师，从事交通运输规划与管理、智能交通研究；E-mail:yangxg@tongji.edu.cn

U491

A

1672-7207(2016)07-2528-09

10.11817/j.issn.1672-7207.2016.07.047

2015-07-10；

2015-09-10

国家自然科学基金资助项目(51468020，51238008)；江西省自然科学基金资助项目(20142BAB207016)；中国博士后科学基金资助项目(2014M561519)(Projects(51468020,51238008)supported by the National Natural Science Foundation of China; Project(20142BAB207016)supported by the Natural Science Foundation of Jiangxi Province;Project(2014M561519)supported by the China Postdoctoral Science Foundation)