钢框架结构基于能量的塑性设计方法

胡淑军，王湛(.南昌大学 建筑工程学院，江西 南昌，33003；.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州，50640)

钢框架结构基于能量的塑性设计方法

胡淑军1，王湛2
(1.南昌大学 建筑工程学院，江西 南昌，330031；
2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州，510640)

以“强柱弱梁”的屈服机理为前提，结合建筑抗震设计规范和能量平衡原理得到结构的基底剪力和各楼层的剪力，提出钢框架结构基于能量的塑性设计方法。该方法还需预先确定结构在罕遇地震下的目标位移和耗能折减系数η，并通过塑性设计法对各构件进行设计。利用Perform-3D软件对所设计结构进行非线性动力时程分析。研究结果表明：该方法可设计不同抗震设防烈度下的钢框架结构，且无需进行复杂的计算和迭代，就能使结构满足多遇及罕遇地震下的预定功能。

钢框架；能量平衡；塑性设计；屈服机理；耗能折减系数

对于普通钢框架结构，传统的设计方法首先根据基底剪力法等方法确定结构的基底剪力及各楼层剪力，由此确定各构件的内力和截面[1]。在罕遇地震下，这种基于弹性分析所设计的结构被直接用于非弹性分析中，可能无法真实反映出结构预定的屈服机理和功能，并发生较大的非弹性变形和无法预期的破坏。基于能量的抗震设计方法，主要基于能量守恒定理，通过结构的能量平衡方程，分析地震作用下结构能量的输入、耗散和转化，由此控制能量转化的过程[2-4]。目前对于基于能量的抗震设计方法研究很多，且该方法的基础研究已趋于完善[5-7]。它的特点主要在于：1)对于给定的结构，地震输入到结构的能量是1个稳定量，是结构抗震能力的总需求指标；2)设计时需考虑结构体系中耗能部位或耗能构件的合理分布，即结构在罕遇地震下的耗能分布合理，使基于能量设计落实到构件层次；3)在实现结构损伤耗能机制控制的前提下，使结构的总耗能大于预期强震的总输入能量[5]。将结构等效为理想的弹塑性单自由度体系时，地震输入到结构的能量可根据结构质量和拟速度谱等参数确定[8]。LEE等[9]通过修正地震作用下结构输入的能量，重新评估结构在非弹性变形时的能量方程，使所设计的结构更合理和经济。预先选定结构在罕遇地震下的目标位移，并结合能量平衡的原理，可得到结构的基底剪力[10-11]。此外，CHAO等[12]基于非线性分析所提出的侧向力分布方式，可使结构更好地满足非弹性变形下的预期性能，并得到各楼层的剪力。为保证结构的延性和抗震性能，需预先选定结构的屈服单元，即首先被破坏的构件。基于“强柱弱梁”的设计思想，罕遇地震下纯框架结构中的梁应首先屈服，随后柱底屈服[1]。框架梁作为结构的主要耗能构件，耗散大量地震能量，并保证各楼层柱不被破坏，防止结构发生倒塌。各楼层梁端和底层柱底出现塑性屈服所耗散的总能量大于地震所输入的能量时，即可保证钢框架结构的安全性和可靠性。基于该设计思想和各楼层剪力，可使各楼层的框架梁、柱合理分布。本文作者结合基于能量的抗震设计方法，并预先确定结构在罕遇地震下的耗能机理和目标位移，且通过塑性设计法设计各构件，提出钢框架结构基于能量的塑性设计方法。根据结构在目标位移下所输入的能量与非弹性变形时各构件所耗散能量相等的原则，得到结构的基底剪力；考虑耗能折减系数能使结构更简单、合理地满足规范的要求。通过设计某12层钢框架结构，采用非线性动力时程分析验证所提出方法的准确性，并为该方法在钢框架结构中的分析和应用提出相关建议。

1　钢框架结构的侧向力分布

目前，钢框架结构的基底剪力和各楼层剪力分布是根据GB 50010—2010“建筑抗震设计规范”[1]中的静力分析法确定。在罕遇地震下，基于弹性分析所设计的结构将被直接用于非弹性分析，此时可能无法真实反映结构的性能。根据预先选定的目标位移和能量平衡原理，可得到一种基于非弹性分析所得的侧向力分布方式和基底剪力，使所设计的结构更合理和经济[7]。

1.1基于修正的能量平衡法

基于能量的塑性设计方法，需预先确定结构在罕遇地震下的破坏机理和目标位移，并根据能量平衡原理，使结构在目标位移下所作的功与非弹性变形时各构件所耗散的能量相等。

推导钢框架结构的基底剪力时，根据结构在单向加载下达到目标位移时所作的功，与结构假想为单自由度体系时在弹塑性状态下谱反应所产生的能量相等，即地震所输入的能量与耗散的能量相等。因此，基于能量平衡法并考虑能量修正系数，可得到结构在弹塑性状态时的功能方程为[10]

式中：Ee和Ep分别为结构达到目标位移时所需的弹性和塑性能量；Sv为结构的拟速度设计谱；M为结构的总质量；γ为能量修正系数，由γs和Rμ确定；T为结构的基本自振周期[13]；α1为地震影响系数[1]；g为重力加速度。

图1所示为结构达到目标位移时所作的功与所耗散的能量，即基于能量的塑性设计方法的基本理论。当图1中的外功与内功的面积相等时，式可改写成：

根据图1可进一步将式改写成：

目前对于延性系数γs和延性折减系数Rμ的研究已有很多，并对2个参数与自振周期T的关系进行了描述[9]。

AKIYAMA[14]提出了等效单自由度体系的弹性能量方程，可表示为

式中：V和W分别为结构的基底剪力和质量。

将式代入式，可得到塑性能量Ep为

图1　基于能量的塑性设计的能量平衡图Fig.1　Energy balance of energy balance-based plastic design

1.2各楼层剪力的分布方式

当结构遭遇罕遇地震作用时，传统的按弹性分析方法所得的楼层剪力分布方式已不能准确反映结构的实际受力，且可能无法准确模拟结构此时的受力和非弹性变形。基于能量的塑性设计方法中最重要的因素之一，是使用更合理且接近实际的侧向力分布方式，能代表结构在非弹性状态下的侧向力。

CHAO等[12]通过对结构的非线性分析，提出了一种新的侧向力分布方式，使结构在非弹性变形下产生更均匀的层间位移角，并更容易实现结构中的定点屈服和强柱弱梁等抗震设防理念。基于剪力分布系数βi，各楼层的剪力与顶层剪力可表示为

式中：βi为剪力分布系数；Fi和Fn分别为第i层和顶层的剪力；Wj和Wn分别为第j层和顶层的重力；hj和hn分别为第j层和顶层距地面的高度。

根据式，可得到第i层和顶层的楼层剪力与基底剪力的关系，分别表示为：

因此，第i层的楼层剪力可表示为

式中：βi+1为第i+1层的剪力分布系数，当i=n时，βi+1=0。

1.3基于目标位移法的基底剪力

图2所示为预先选定的目标位移和屈服机理下的框架反应图。图2中基于预先选定结构的屈服机理和目标位移，由外部力对结构产生的塑性能量为

式中：pθ是结构的塑性层间位移角，等于目标位移uθ减去屈服位移yθ。

将式代入式，可得V/W的表达式为

式中：λ为量纲一的参数。当结构的质量和层高度一定时，λ主要与结构的自振周期T和目标侧移θphn有关，具体表示为

因此，根据上述基底剪力及楼层剪力的计算公式，可得到结构的非弹性侧向力。

图2　预先选定的目标位移和屈服机理下的框架反应图Fig.2　Frame structure in target drift response state with pre-selected yield mechanism

2　钢框架结构基于能量的塑性设计方法

为保证结构的延性和抗震性能，需预先选定结构在罕遇地震下首先屈服的单元。基于“强柱弱梁”的设计思想，罕遇地震下框架梁应首先屈服，随后柱底屈服。梁作为结构的第1道抗震设防线耗散大量地震能量，并防止各楼层柱被破坏。因此，设计时需首先确定各楼层梁的内力和截面的面积，柱的内力是基于梁而得到。

2.1基于耗能折减系数的框架梁设计

罕遇地震下，为使纯框架结构耗散更多的地震能力，并保证主体结构不被破坏，需合理确定结构的破坏机理。如图1所示，假设每层梁两端首先屈服并耗散大量能量，随后底层柱底也出现屈服。基于框架梁与柱底所耗散的能量与外力所做的功相等的原理，可得到各层梁所需塑性弯矩：

式中：Mpbi为第i层梁所需的塑性弯矩；Mpc为底层柱所需的塑性弯矩。

由于结构中各截面面积与受力有关，各楼层沿高度方向的强度应与楼层剪力的分布相同较合理。此时，Mpbi可表示为βiMpbn(其中，Mpbn为顶层梁所需的塑性弯矩)。因此，式可改写为

基于能量的塑性设计所得的结构，由于假设罕遇地震下所有楼层梁端都屈服，这可能与实际情况不相符，且会导致所设计的梁、柱截面过小，在弹性和弹塑性分析时无法满足规范的要求。此时，可假设各楼层仅有部分梁端发生屈服并耗能，即考虑结构的耗能折减系数η，并建议取0.5~1.0。通过考虑该系数可增大梁、柱截面，并使所设计结构更容易达到预期性能和满足规范要求。式可表示为

在罕遇地震下，当结构底层柱底出现塑性铰时，不仅可以耗散大量的地震能量，而且对结构的整体性能影响不大。选择合适的底层柱截面，是保证结构底层柱底出现塑性屈服的重要因素。如图3所示，假设最底层柱的上、下端均出现塑性铰，考虑底层柱的塑性变形与剪力所作功相等的原则，可表示为

式中：h1为底层楼的高度；φ为考虑构件由于硬变强化所引起的超强系数，建议取1.1[9]；θ为假定的转角。整理该式可得

当底层柱的塑性弯矩和各楼层的剪力已知时，可得到顶层梁及各楼层梁的塑性弯矩，并确定其他楼层梁截面的面积。

图3　底层柱形成塑性铰的钢框架结构Fig.3　Steel frame with plastic hinge at bottom columns

2.2柱设计

在框架结构中，为保证结构在目标位移下仍能形成预期的“强柱弱梁”的塑性机制，需在梁单元屈服后，柱仍处于弹性。因此，各楼层柱的内力应在框架梁内力的基础上乘以放大系数ξ。

结构中考虑边柱和中柱的隔离体如图4所示。当柱在梁端形成塑性铰并考虑放大系数ξ时，需重新计算对柱隔离体中各楼层的侧向力。此时，各楼层边柱剪力Fbi和中柱剪力Fzi的分布方式与各楼层梁的内力分布方式相同。

此外，分析时还应考虑各层中梁端剪力对柱产生的弯矩Vpbid/2，如图4(c)所示，d为柱截面的高度。如图4(a)，对于边柱，根据弯矩平衡方程可得

式中：Fbn为顶层边柱的剪力；Vpbi为第i层梁端的塑性剪力，等于2Mpbi/Li；L为梁的长度；ξi为第i层内力放大系数，建议取1.0~1.1[11]。

如图4(b)所示，对于中柱，根据弯矩平衡方程可得

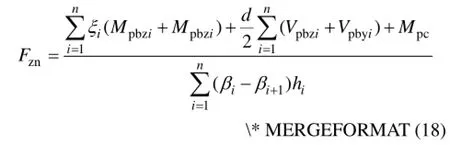
式中：Fzn为顶层中柱的剪力；Mpbzi和Mpbyi分别为第i层梁左端和右端的塑性弯矩；Vpbzi和Vpbyi分别为第i层梁左端和右端的塑性剪力。

柱设计时，假定各中柱或边柱隔离体中所有梁端同时达到塑性屈服可能过于保守，且各楼层的侧向力分布是由基本自振周期等因素确定，未考虑高阶模态的影响，这对上部楼层的影响会比较大。因此，对所有楼层的梁采用相同的超强系数是合理的。重新确定边柱和中柱隔离体的顶层剪力Fbn和Fzn后，将图4中的柱隔离体当成悬臂杆，各层边柱的弯矩可表示为

式中：Mcb(h)为距地面高度为h处边柱的塑性弯矩；Fbi是各楼层剪力，等于(βi-βi+1)Fbn；δi为阶梯函数[10]，具体表示为

同理，各楼层中柱的弯矩可表示为

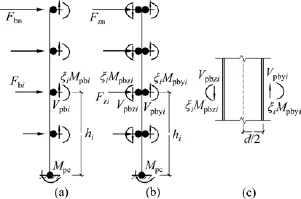
图4　柱的隔离体图Fig.4　Free body diagram of columns

式中：Mcz(h)是距地面高度为h处中柱的塑性弯矩；Fzi是各楼层剪力值，等于(βi-βi+1)Fzn。

距地面高度为h处柱的轴力可表示为

式中：Pc(h)和Pcg(h)为距地面高度h处柱的轴力和荷载、自重对柱产生的轴力。在分别确定柱的轴力和弯矩后，可对柱进行塑性设计。

3　钢框架结构基于能量的塑性设计步骤

合理设计的钢框架结构，强度和延性是2个主要因素。因此，钢框架的设计可总结为以下2点：

1)合理设计框架梁截面，以满足强度和变形的要求；

2)基于所得到的框架梁截面，合理设计框架柱，以保证这些构件在罕遇地震下不发生屈服。

合理设计的钢框架结构不仅具有良好的抗震性能，且有较好的经济性。本文提出了一种钢框架结构的基于能量的塑性设计方法，步骤如下。

1)基底剪力和楼层剪力。在预估结构的自振周期、结构总质量和目标侧移后，基于能量平衡的原理，可得到结构的基底剪力和各楼层剪力。

2)单元设计。在得到结构的基底剪力和各楼层的侧向力后，假设非弹性变形仅发生在各楼层的梁端和底层柱底，并基于能量平衡原理，可得到各层梁的塑性模量，确定梁截面大小；再对边柱和中柱取隔离体分析，并确定各层柱的弯矩与轴力，即可得到各层柱截面的大小。具体流程如图5所示。

4　算例

某钢框架办公楼，共12层，平面图和计算简图如图6所示。各层层高均为3.3 m，结构总高度为39.6 m。结构的设防烈度为8度(0.2g，1g=9.8 m/s)，场地类别Ⅱ类，设计地震分组为3类，弹性分析时特征周期是0.45 s，罕遇地震下的特征周期取0.5 s。各楼层的恒荷载(包括120 mm厚的压型钢板组合楼盖)为5.5 kN/m2，活荷载为2.0 kN/m2。

4.1钢框架结构的设计

采用基于能量的塑性设计对结构设计时，进行2个基本假定：1)结构的屈服位移和极限位移分别为0.5%和2.0%；2)在罕遇地震下，结构的屈服仅发生在各楼层的梁端和底层柱底。

图5　基于能量的塑性设计方法流程图Fig.5　Flow chart of energy-based plastic design

图6　钢框架结构平面图和计算简图Fig.6　Floor plan and calculation plan of steel frame

根据GB 50009—2012“建筑结构荷载规范”[13]中对结构的基本自振周期近似计算方法，可得T1= 0.15×12=1.8 s，并由GB 50010—2010“建筑抗震设计规范”[1]确定罕遇地震影响系数α1及各参数。由于每层中各榀框架的梁、柱截面相同，取单榀框架分析即可。W为单榀框架中结构的总重力，包括结构的恒载和活载所产生的重力。各设计参数值如表1所示。

在确定各设计参数后，可根据表2中所得到的剪力分布系数βi等，并结合图5中的方法得到基底剪力和各楼层剪力，由此可得到钢框架结构中各楼层梁与柱的内力和截面面积。梁柱截面均以截面高度h，翼缘宽度b，腹板厚tw和翼缘厚度bf的H型截面(即h×b×tw×bf，单位：mm×mm×mm×mm，下同)。

4.1.1梁的设计

在得到结构的基底剪力V后，将结构的耗能折减系数η取0.5，并考虑底层柱底可能发生的屈服，可得到底柱底屈服弯矩Mpc=1.1×313×3.3/8=142 kN·m。根据图5中的相关设计流程，可得到各楼层的梁截面面积，如表2所示。

表1　某十二层钢框架基于能量的塑性设计参数Table 1　Design parameters for 12-storey energy-based plastic design frame

4.1.2柱的设计

假设柱截面的高度为0.4m，且各楼层的超强系数ξi均取1.1，由式和式计算得到的边柱和中柱的顶层剪力Fbn和Fzn分别为33.4 kN和65.4 kN。此时各楼层边柱与中柱的最大弯矩和轴力，以及各层柱截面面积，如表3所示。

4.2验证分析

表2　某十二层钢框架基于能量的塑性设计的侧向力及梁的设计Table 2　Design lateral forces and steel beams for 12-storey energy-based plastic design frame

表3　某十二层钢框架钢柱的内力和截面Table 3　Design forces and sections of steel columns for 12-storey energy-based plastic design frame

弹性分析时，采用Midas-building和Perform-3D软件对结构进行分析。结构的前3阶基本周期分别为2.87，2.61，2.35和2.73，2.49和2.25 s，前3阶振型分别以X向平动、Y向平动和扭转。

根据GB 50010—2010“建筑抗震设计规范”[1]的规定，选择7组时程曲线，包括6组实际强震记录和1组人工模拟的地震波，分别为Elcent波、Taft波、Holly波、Oakland波、兰州波、唐山波和人工波。对所选择的地震波分析可知，除满足基底剪力的要求外，与振型分解反应谱法所得的曲线对比，前3阶主要振型所对应周期点上的地震影响系数，其平均值相差值均满足小于20%的要求，如图7所示。

图7　七条地震波与反应谱影响系数的对比Fig.7　Comparison of seven seismic waves and response spectrum curve

在多遇地震下，采用2个软件对结构进行反应谱分析，所得的层间位移角相差较小，验证了Perform-3D中模型的准确性。采用Perform-3D对结构进行反应谱分析和弹性时程分析时，最大层间位移角分别是1/358 和1/323，满足规范1/250的要求，且分布较均匀，如图8所示。其他结果均满足规范要求。

在罕遇地震下，采用非线性动力时程分析方法评估结构的反应。梁采用弯矩铰，柱采用P-M-M铰，各铰的力学性能基于FEMA356[15]确定。

基于Perform-3D软件，并采用所选择的7条地震波对结构进行分析可知，各楼层的最大层间位移角从上至下逐渐增大，且沿楼层均匀分布，如图9所示。其中，唐山波和Oakland波的最大层间位移角分别为1/53和1/58，接近且满足规范[1]中1/50的要求。因此，从结构的整体层面上分析可知，所设计的结果满足要求且与预期性能相近。

从图8和图9可知：由基于能量的塑性设计方法所设计的钢框架结构，能简单、合理地满足结构的预定功能和相关规范的要求，验证了所提出方法的准确性。

在Oakland波作用下结构达到极限状态时，各构件的屈服顺序如图10所示。各楼层梁端逐渐屈服，随后柱底也发生屈服，且仅底层柱底发生屈服，与预期的屈服机理吻合较好，满足预期的“强柱弱梁”的设计思想。此外，所设计结构的顶层位移虽未达到预定的目标位移，但最大层间位移角非常接近规范限值，即认为结构达到了预定目标。

图8　多遇地震下各楼层的层间位移角Fig.8　Interstory drift ratio under frequent earthquake for steel frame

图9　罕遇地震下各楼层的层间位移角Fig.9　Interstory drift ratio under rare earthquake for steel frame

从图10还可看出：该钢框架结构达到极限状态时，所有楼层中仅有一半梁端发生屈服，且梁每端是先后进入屈服，所耗散的能量也有不同。因此，结构耗能折减系数η取0.5合理。

图10　罕遇地震钢框架在目标位移时的塑性铰分布Fig.10　Plastic hinges distribution under rare earthquake at target drift for steel frames

5　结论

1)采用推导的基于能量的塑性设计方法对钢框架结构设计时，无需进行复杂的计算和迭代，就能使所设计结构满足多遇及罕遇地震作用下的屈服机理、目标侧移和规范中的相关要求。

2)在所推导的基于能量的塑性设计方法中，考虑耗能折减系数能使结构更简单、合理地满足规范要求。

3)基于能量的塑性设计方法可用于设计不同抗震设防烈度下的钢框架结构。

[1]GB 50010—2010,建筑抗震设计规范[S]. GB 50010—2010,Code for seismic design of buildings[S].

[2]RIDDELL R,GARCIA J E.Hysteretic energy spectrum and damagecontrol[J].EarthquakeEngineering&Structural Dynamics,2001,30(12):1791-1816.

[3]CHOU C C,UANG C M.A procedure for evaluating seismic energy demand of framed structures[J].Earthquake Engineering &Structural Dynamics,2003,32(2):229-244.

[4]BOJORQUEZ E,RUIZ S E,TERAN-GILMORE A.Reliabilitybased evaluation of steel structures using energy concepts[J]. Engineering Structures,2008,30(6):1745-1759.

[5]叶列平,程光煜,曲哲,等.基于能量抗震设计方法研究及其在钢支撑框架结构中的应用[J].建筑结构学报,2012,33(11): 36-45. YE Lieping,CHENG Guangyu,QU Zhe,et al.Study on energy-based seismic design method and application on steel braced frame structure[J].Journal of Building Structures,2012, 33(11):36-45.

[6]缪志伟,马千里,叶列平.钢筋混凝土框架结构基于能量抗震设计方法研究[J].建筑结构学报,2013,34(12):1-10. MIAO Zhiwei,MA Qianli,YE Lieping.Study on energy-based seismic design method of reinforced concrete frame structure[J]. Journal of Building Structures,2013,34(12):1-10.

[7]HABIBI A,CHAN R W K,ALBERMANI F.Energy-based design method for seismic retrofitting with passive energy dissipation systems[J].Engineering Structures,2013,46(1): 77-86.

[8]UANG C M,BERTERO V V.Use of energy as a design criterion inearthquake-resistantdesign[M].Berkeley:Earthquake Engineering Research Center,University of California,1988: 1-26.

[9]LEE S S,GOEL S C,CHAO S H.Performance-based seismic design of steel moment frames using target drift and yield mechanism[J].The 13th World Conference on Earthquake Engineering,Vancouver,2004:266.

[10]LEELATAVIWAT S.Drift and yield mechanism based seismic design and upgrading of steel moment frames[D].Ann Arbor: Department of Civil and Environment Engineering,University of Michigan,MI,1998:47-54.

[11]LEELATAVIWAT S,GOEL S C,STOJADINOVIC B.Toward performance-based seismic design of structures[J].Earthquake Spectra,1999,15(3):435-461.

[12]CHAO S H,GOEL S C,LEE S S.A seismic design lateral force distribution based on inelastic state of structures[J].Earthquake Spectra,2007,23(3):547-569.

[13]GB 50009—2012,建筑结构荷载规范[S]. GB 50009—2012,Load code for the design of building structures[S].

[14]AKIYAMAH.Earthquake-resistantlimit-statedesignof buildings[M].Tokyo:University of Tokyo Press,1985:256-278.

[15]FEMA-356.Prestandard and commentary for the seismic rehabilitation of buildings[S].

(编辑罗金花)

Study of energy-based plastic design method on steel frame structures

HU Shujun1,WANG Zhan2
(1.School of Civil Engineering andArchitecture,Nanchang University,Nanchang 330031,China;
2.State Key Laboratory of Subtropical Building Science,South China University of Technology, Guangzhou 510640,China)

The energy-based plastic design method of steel frame structures was proposed based on the‘strong column weak beam’energy dissipation and yield mechanism under the inelastic seismic behaviors.The base shear and lateral force distribution were derived from modified energy balance equation and the code for seismic design of buildings. Moreover,the pre-selected target drift and the reduced energy dissipation coefficient η were also important to the proposed method,and all the elements were obtained by plastic design method.Nonlinear dynamic time-history analysis was carried out by Perform-3D.The results show that the frames with different seismic precautionary intensities designed by the proposed method can exhibit expected functions during frequent and rare earthquake without complicated iteration and calculation.

steel frame;energy balance;plastic design;yield mechanism;reduced energy dissipation coefficient

胡淑军，博士，从事钢结构抗震及优化研究；E-mail:husj.1229@163.com

TU393.2，TU973

A

1672-7207(2016)07-2476-09

10.11817/j.issn.1672-7207.2016.07.040

2015-07-18；

2015-09-22

国家自然科学基金资助项目(51378219，51378009)；江西省博士后科研择优资助项目(2015KY49)(Projects(51378219, 51378009)supported by the National Natural Science Foundation of China;Project(2015KY49)supported by Jiangxi Postdoctoral Foundation OptimumAid)