径向偏移对球阀液固两相流场及流通特性的影响

马艺，张生昌，马中强，邓鸿英，张志鸿（. 浙江工业大学 化工机械设计研究所，浙江 杭州，3004；2. 过程装备及其再制造教育部工程研究中心，浙江 杭州，3004）

径向偏移对球阀液固两相流场及流通特性的影响

马艺1， 2，张生昌1， 2，马中强1，邓鸿英1， 2，张志鸿1
（1. 浙江工业大学 化工机械设计研究所，浙江 杭州，310014；2. 过程装备及其再制造教育部工程研究中心，浙江 杭州，310014）

基于球阀基本动力学分析，利用 CFD数值模拟手段对往复式液固混输泵的咽喉部件，即排出球阀开展研究，分析阀球径向偏移对高浓度两相流场的影响，预测球阀内部体积分数和压力场分布状态，并进一步考察在各开启高度和固相质量分数下，球阀所受作用力和流通能力随偏移距离的变化规律。研究结果表明：球阀偏移相反侧存在严重的二次涡流，固相颗粒呈驼峰状分布；阀球所受作用力随径向偏移的变化趋势与进出口压降较为相似，各影响因素对其径向分力的显著程度由大到小顺序为：开启高度，阀球偏移距离，固相质量分数；当固相质量分数由20%增至80%时，球阀的流量系数变化范围为0.38～0.70，液固两相流通能力随阀球径向偏移略有波动。

球阀；两相流；浓度场；液动力；流量系数

液压驱动往复泵具有结构简单、流量均匀、耐磨损等特点，在输送高浓度、高黏度复杂介质时具有突出优势，是国内外产品附加值较高的高新技术泵类之一［1-3］。在输送高浓度液固两相流时，往复泵液力端将其加压至排出球阀底部［4］，推开阀球，阀球迅速升起，从而实现排出过程，因此，在高浓度工况下排出球阀的启闭过程及内部流动状态直接决定着往复泵的运行效率和可靠性。目前，排出阀的研究工作主要集中于纯液相或低浓度液固两相工况［5-7］，且将阀球/阀芯近似为沿轴线升降运动，阀腔内部流场呈轴对称分布［8-10］。但是在实际工作时，受变工况、漩涡流动及滞后作用等影响，排出阀阀球附面受力易出现波动［11］，其运动可能偏离轴线方向，而目前这种径向偏移对排出阀性能的影响规律尚不明晰，尤其是在两相流动下其变化趋势更为复杂。因此，本文作者针对不同径向偏移时液固排出球阀内部两相流动状态进行模拟研究，以球阀基本运动方程为理论基础，分析球阀所受作用力、流量系数的影响因素及变化规律，为后续球阀动态特性及滞后过程的研究奠定理论依据。

1　球阀基本动力学微分方程

球阀基本工作原理如图1所示。为便于研究，假设如下：1） 阀腔内部流体为均一连续不可压流体，各点物性参数相同；2） 忽略流体在阀腔内部的摩擦阻力；3） 忽略阀球自身的旋转运动。

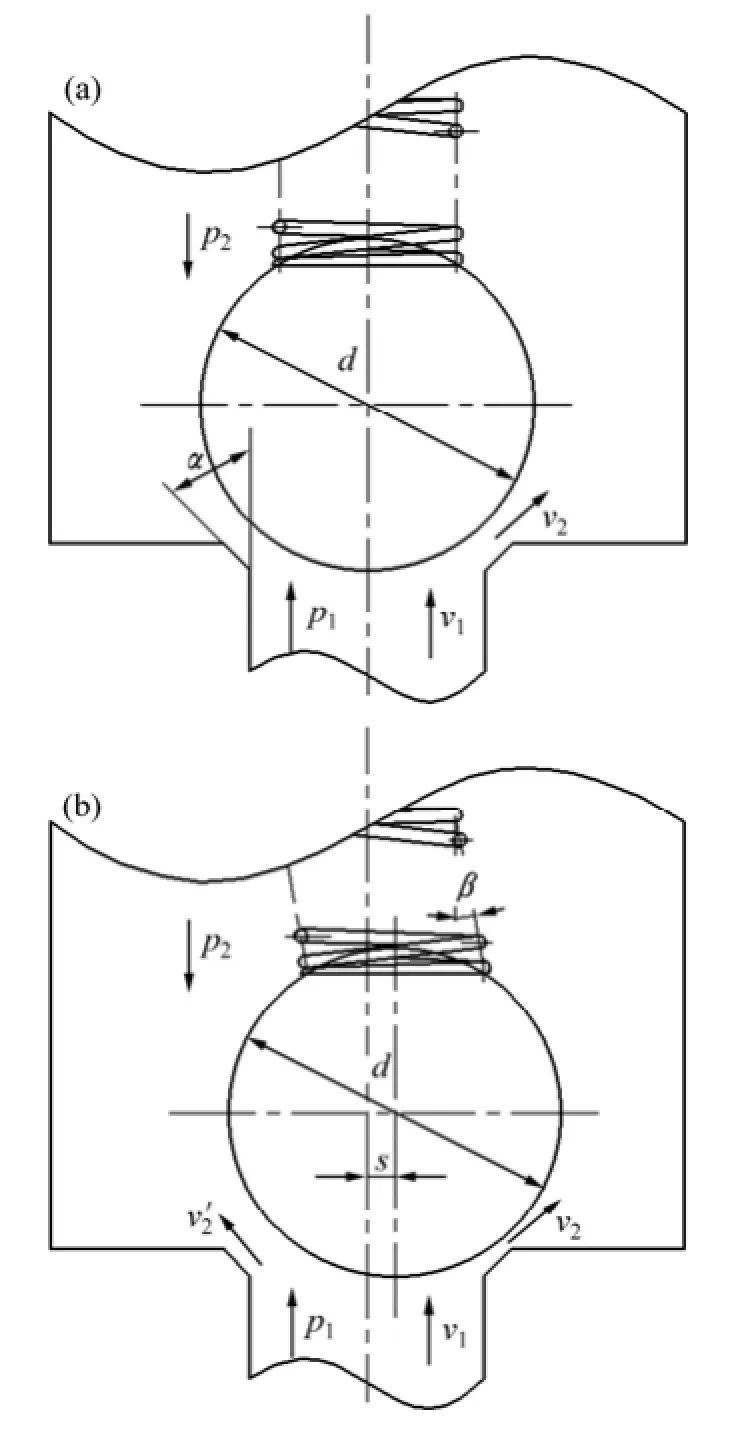
图1　球阀工作示意图Fig. 1　Schematic diagram of ball valve’s working process

1.1阀球沿轴向运动

当阀球沿轴线做单自由度运动，无径向偏移时，如图1（a）所示。图1（a）中：d为阀球直径；α为阀座半锥角；p1为阀口压力；p2为阀球中后部压力；v1为阀口速度；v2为流经阀隙流速。

当排出阀工作时，阀球受到重力G、上部弹簧力Fs及周围流体的综合作用。

1） 弹簧弹力Fs。其表达式为

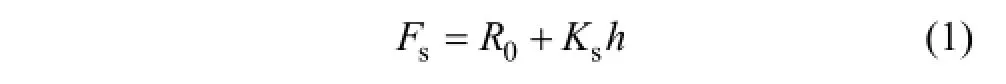
式中：R0为弹簧预紧力；Ks为弹簧弹性系数；h为阀球开启高度。

2） 流体对阀球的作用力Ff。该作用力由阀球表面轴径向压力差产生的作用力Fp、流体动量变化所产生的反作用力（即液动力Ff1）等所致。

其中后者又由稳态液动力 Fw和瞬态液动力 Fu2部分组成，其计算式可由动量定理计算，即

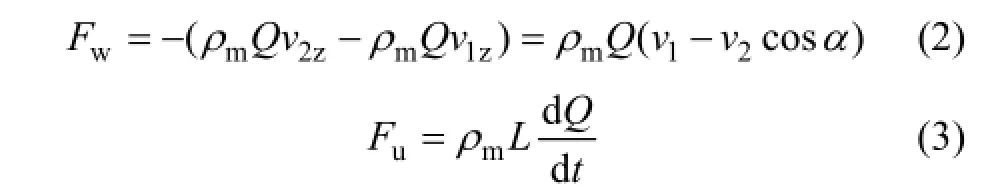
式中：ρm为混合密度，，其中φ为固相体积分数， ρs为固相密度， ρl为液相密度；Q为两相流体积流量； v2z为阀隙流速的轴向分量； v1z为阀口流速的轴向分量；L为特征长度；t为时间。

所以流体对阀球的作用力Ff可表示为

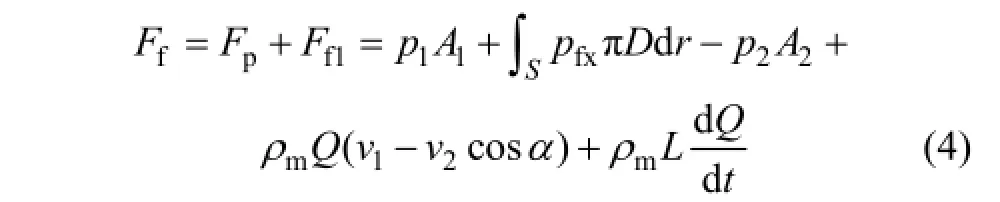
式中：A1为阀球下部受压面积；pfx为阀口静压力；A2为阀球中上部受压面积。

由此建立球阀的动力学微分方程为

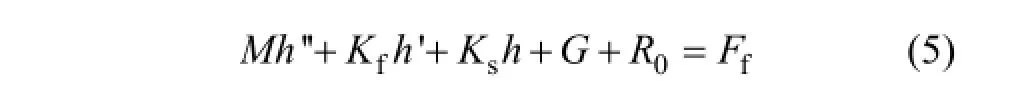
即

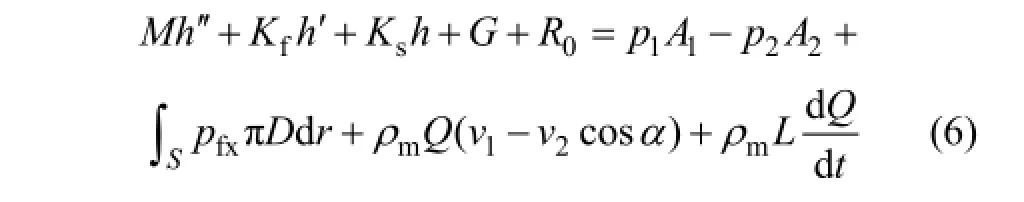
式中：M 为阀球和弹簧的当量质量；Kf为运动阻尼系数。

1.2阀球沿径向运动

当阀口来流或者阀座上部涡流对阀球造成径向轻微的扰动时，阀球出现径向偏移，如图1（b）所示。图1（b）中：s为偏移距离；β为对应弹簧倾斜角；v2和v2′分别为阀隙两侧出口速度。

就阀球径向运动而言，弹簧弹力Fs随之产生径向分量Fsr，即

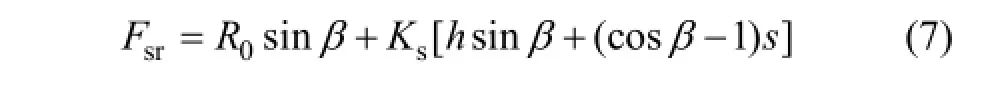
但阀隙区域形状的不规则化使阀隙静压力和液动力的求解较为困难，同时，受偏移作用的影响，在非轴对称场下两相流分布状态发生变化，将阀球前后压力近似处理为某一定值的方法不再适用。因此，有必要采用数值模拟的方法首先对球阀内部固相分布和压力场随径向偏移的变化规律进行研究，并进一步确定球阀所受作用力及流量系数的变化特性。

2　计算模型及初始条件

出口球阀的主要设计工况为：六缸液压往复泵、流量为100 m3/h、输送高浓度水煤浆。其中水煤浆的基本物性条件为固相质量分数w为60%（对应体积分数为51.5%）、颗粒粒径dp=50 μm、混合黏度μ=1.8 Pa·s。

建立球阀的三维轴对称模型，其主要结构参数见表1。以球阀入口截面为z=0基准截面，阀座上、下顶角轴向高度分别为 z1=30 mm和 z2=20 mm。利用Gambit软件对球阀内部流道进行网格划分，并验证了网格无关性，最终采用网格数为385 317的三维模型进行模拟计算。

考虑到阀座上部涡流及两相流动工况，采用雷诺模型［12-13］和双流体模型［14-15］研究球阀内部液固流场，通过有限体积法［16］和SIMPLE算法求解离散方程，残差标准均取为10-5，选取不同阀球开启高度（h=5，9，13，17 mm）、相对径向偏移距离（s/h=0，0.2，0.4，0.6，0.8）进行仿真。

表1　球阀基本结构参数Table 1 Structural parameters of ball valve

3　计算结果及讨论

3.1模拟结果准确性验证

采用雷诺模型及相关模拟方法，以插装式背压阀为对象进行仿真计算，并与邵森寅［17］所得的试验结果进行比较，如图2所示。由图2可知：模拟所得结果与试验数据吻合相对较好，在流量为60 m3/h时误差达最大值。因此，通过试验数据与模拟结果的比较，本文采用的湍流模型及数值解法较适用于球阀流场的数值模拟。

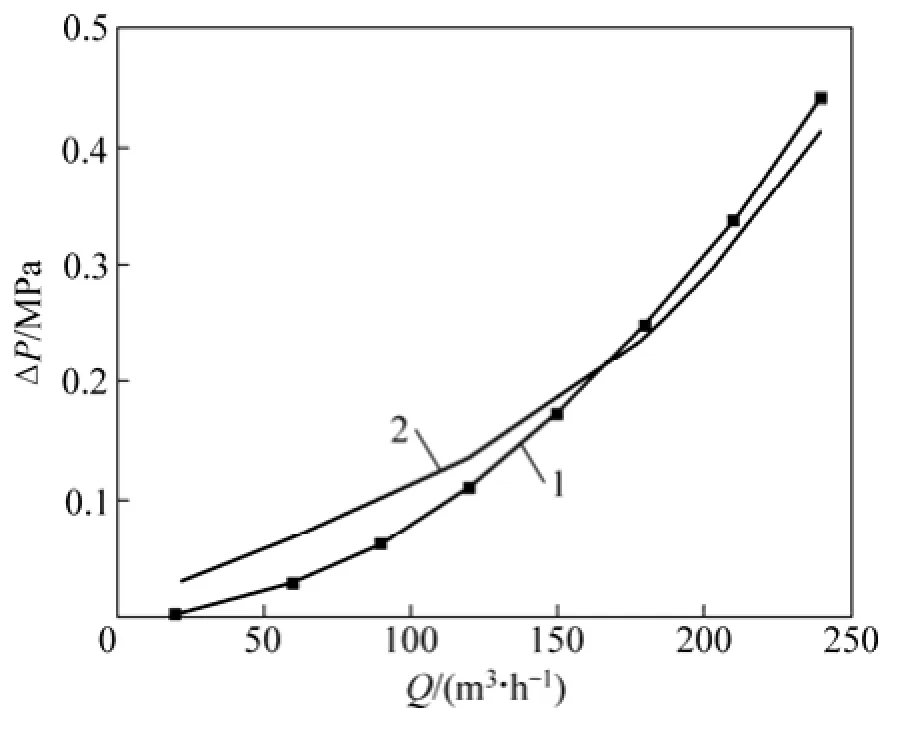
图2　模拟方法准确性验证Fig. 2　Accuracy verification of simulated method

3.2球阀内部两相流动特征

颗粒的速度变化和体积分数场反映了球阀工作过程中液固两相的流动状态，选取两典型横剖面—窄阀隙出口z=30 mm和阀球最大直径所在截面z=z（dmax），研究阀腔内固相颗粒的流动规律，分析不同阀球开启高度h下固相最大无量纲速度vmax/vi（即最大速度与入口速度之比）随阀球径向偏移的变化曲线，如图 3所示。

由图3可见：对于截面z=30 mm，当流量一定时，各开度下截面最大流速均随阀球偏移距离增加而增大，尤其在s/h为0.8时达到了无偏移时的2.25倍以上。但当h≤9 mm时，最大流速近似呈线性变化，而当h＞9 mm时，变化趋势逐渐减缓。这是由于偏离侧流道的内壁面效应不断增强，部分流体转而由流通面积逐渐扩大的相反侧流出。

对于截面 z=z（dmax），流通面积和流量均为定值，经分析得s/h＞0时，各阀球开启高度下截面平均流速基本一致，且最大流速数值仅为阀隙出口的0.18～0.40倍，但受到窄阀隙射流及流动惯性的影响，截面最大流速随偏移距离的变化梯度均大于窄阀隙出口截面。

以截面 z=z（dmax）为基准，进一步分析球阀半开和全开状态（h=9 mm和h=17 mm）下球阀内部径向固相体积分数的变化规律，如图4所示。由图4可以看到：当s/h=0时，2种阀球开启高度下固相颗粒均倾向于紧贴阀球壁面绕流而行，体积分数随径向位置r增加而减小，在阀腔内壁降至最小值。随着径向偏移距离的增加，阀球两侧的体积分数分布差异更加明显，以全开状态h=17 mm为例，偏离侧体积分数分布逐渐平缓，接近平推流流态，固相颗粒较为富集，相反侧则变化为较明显的“驼峰”状分布。

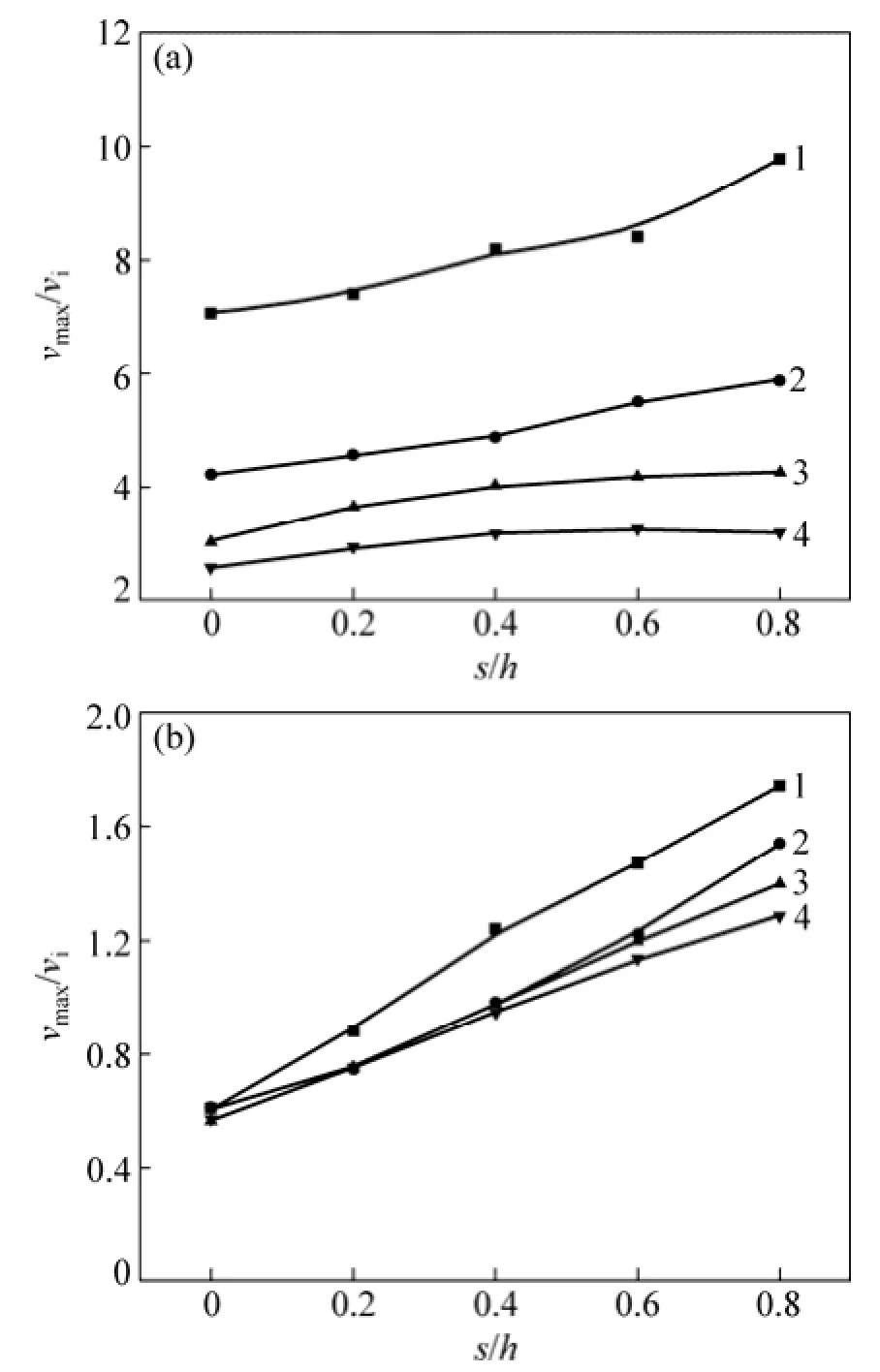
图3　各阀球开启高度截面最大速度随阀球径向偏移的变化Fig. 3　Changes of maximum velocities in cross sections with ball’s radial displacement under different value’s opening heights

3.3球阀内部压力场分布规律

开启压力是阀球升起的直接诱导力［18］。球阀半开和全开时阀腔纵剖面压力随阀球径向偏移的分布状态如图5所示。

由图5可知：当s/h=0时，流体运动轨迹呈轴对称分布，静压力递减区域主要集中于窄阀隙20 mm≤z≤30 mm区域，阀座上部特别是阀球后部静压力p2变化可忽略。

随着径向偏移距离逐渐增大，偏离侧流道内压力梯度更明显，相反侧则相对平缓。阀腔内部压力波动范围延伸至阀球后部，阀球上顶点处压力低于1.0 MPa，易引起出口附近回流现象产生。且阀座上部30 mm＜z≤50 mm二次流加剧，部分两相流可能积聚于旋涡区内，造成颗粒沉积及阀座磨损。因此，在径向压差和环向涡流的作用下，阀球偏离侧被挤压的流体对阀球产生斜向上的推动力。

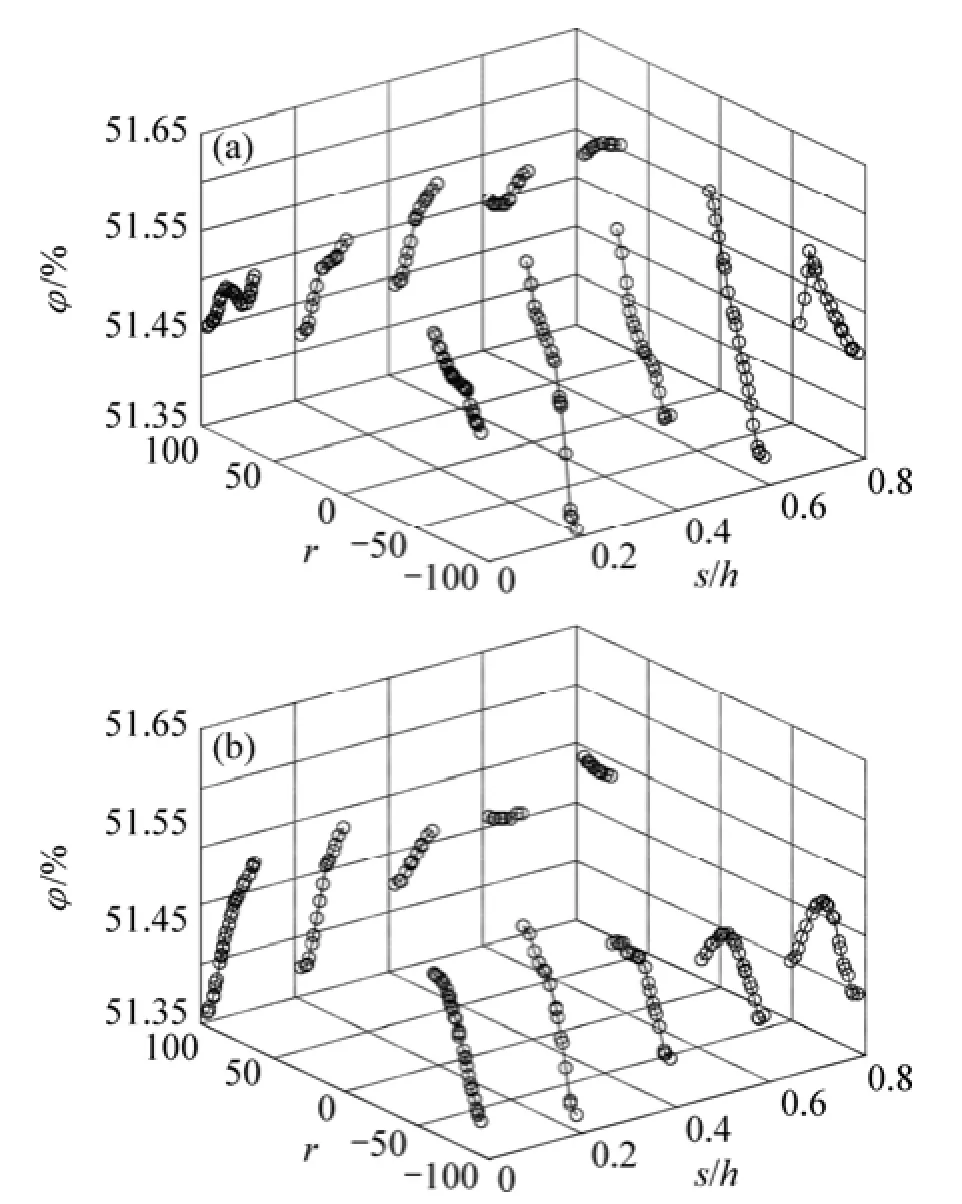
图4　各阀球开启高度固相体积分数随径向偏移的分布Fig. 4　Distributions of solid volume fraction with ball’s radial displacement under different value’s opening heights

图6所示为球阀压降随径向偏移的变化规律。由图6可知：当球阀全开（h=17 mm）时，流体流动阻力减弱，进出口压降随偏移距离的增加而减小；当5 mm≤h≤13 mm时，球阀压降均在s/h=0.2处达到一极值点，但在阀球开启高度较小时压降递减后突跃，数值达到了全开时的13倍以上。由球阀内部两相流动特征可知：当阀球开启高度较大时，部分流体运动轨迹迁移转向，缓解了窄阀隙壁面边界层对流动的阻碍作用，但在阀球开启高度较小且偏离距离较大时，涌入偏离侧的高浓度液固两相易发生拥堵卡塞，阀隙效应显著。

3.4阀球所受作用力Ff

阀球的总作用力关系着隔膜泵排出系统的可靠性和稳定性［19］，不仅会影响阀球的升程位移瞬时变化，且可能诱发阀球的振动。按方向可将其分为轴向分力和径向分力，当阀球出现径向偏移时径向分力的影响不容忽略。

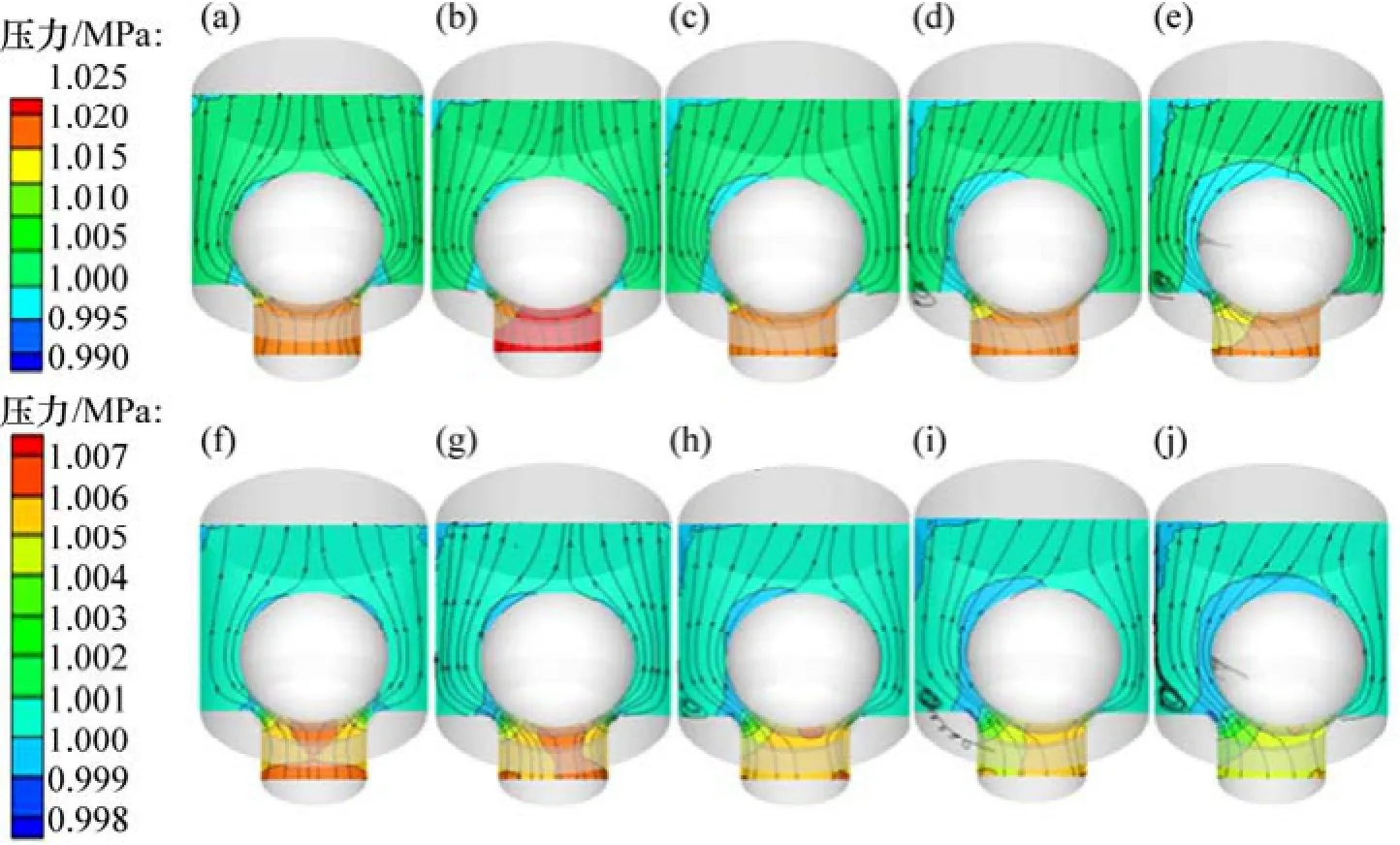
图5　球阀纵剖面静压力分布云图Fig. 5　Contours of static pressure in longitudinal section of ball valve

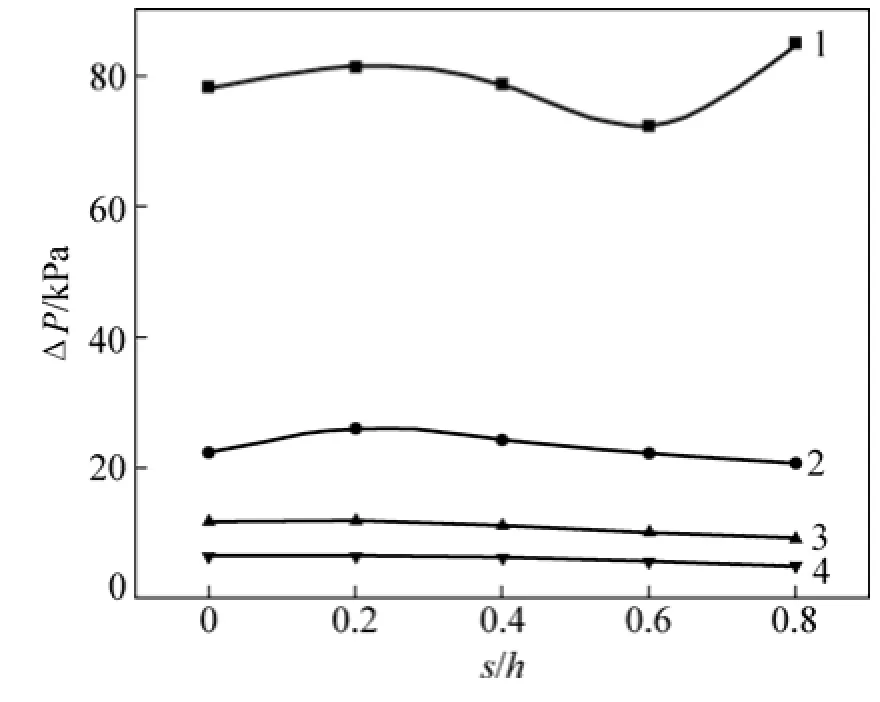
图6　各阀球开启高度球阀压降随径向偏移的变化Fig. 6　Changes of pressure drop with ball’s radial displacement under different value’s opening heights

定义θ为总作用力与水平方向夹角，通过对阀球壁面压力进行积分得各阀球开启高度下阀球受力随径向偏移的变化规律，见图7。

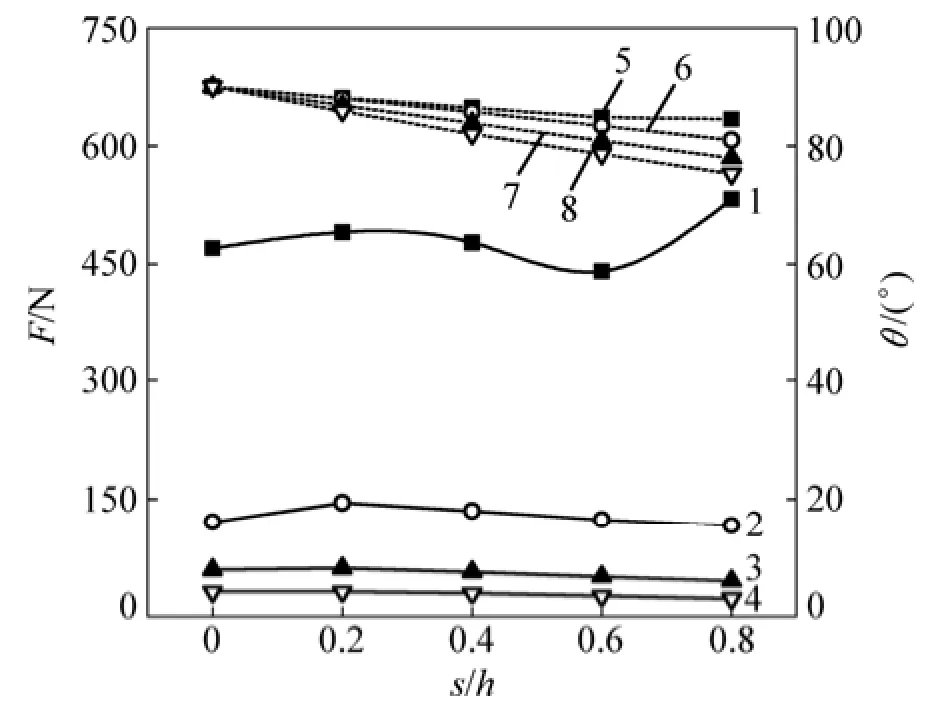
图7　各阀球开启高度总作用力随径向偏移的变化Fig. 7　Changes of total force with ball’s radial displacement under different value’s opening heights

固定阀球径向偏移量，阀球开启高度越大，作用力F和夹角θ越小，阀球径向分力所占比例越大，其中在h=17 mm时占到了总作用力的25.5%。固定球阀开度，作用力数值与进出口压降随径向偏移的变化规律基本相同，夹角则随径向偏移量增加而单调递减。当开度h=5 mm、阀球偏移量s/h为0.8时，阀球总作用力和径向分力分别为全开h=17 mm时的23.5倍和8.8倍，因此，径向偏移对阀球所受作用力的影响较对压降更明显，并且偏移过程中轴、径向分力不断重新动态分配，球阀的启闭及滞后时间大大延长。

由式（2）可知：在出口流量Q和阀座半锥角α一定的情况下，液动力主要受到不同h时的固相质量分数w（或体积分数φ）的影响。因此，分析不同固相质量分数下球阀半开和全开时阀球作用力随径向偏移的变化规律，见图8。

由图8可以看出：在2种开度下，当固相质量分数由20%增至80%时作用力数值变化较均匀，梯度略有增大，波动幅度分别达 11.1%和 30.3%，即高浓度下阀球径向偏移对作用力的影响较为显著。并且不同径向偏移量时阀球作用力角度均呈线性变化，随固相质量分数的提高而增大。

采用下式对阀球偏移距离s、阀球开启高度h、固相质量分数w与轴、径向作用分力Fz和Fr的关系进行回归，即

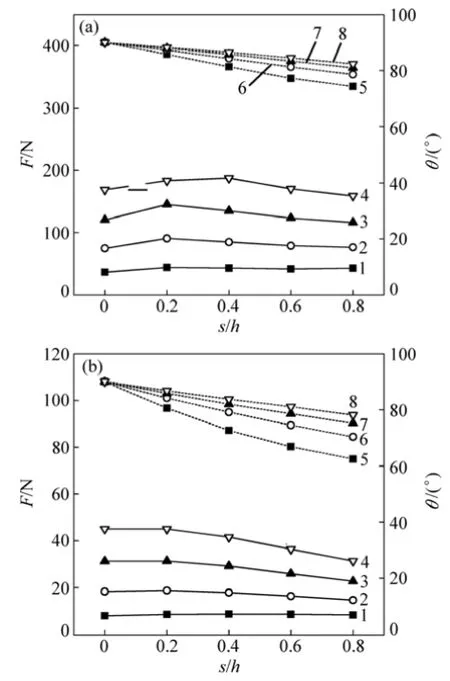
图8　不同固相质量分数下总作用力随径向偏移的变化Fig. 8　Changes of total force with ball’s radial displacement under different solid mass fractions

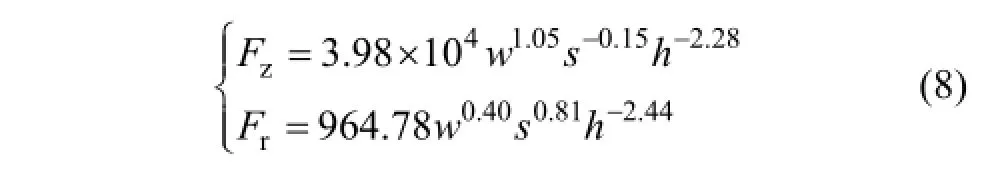
经比较可得各影响因素的显著程度。

轴向作用力显著程序由大到小顺序为阀球开启高度h、固相质量分数w和阀球偏移距离s。

径向作用力显著程序由大到小顺序为阀球开启高度h、阀球偏移距离s和固相质量分数w。

3.5球阀流量系数

流量系数Cd是衡量球阀流通能力的关键指标［20］，其表达式为

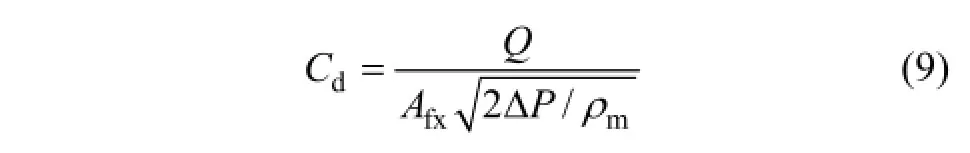
式中：Afx为阀口流通面积。

图9所示为球阀流量系数的变化曲线。当液固两相流经阀口时，由于流体与壁面及流体与固体颗粒间的作用增强，阀口液阻增大，流通能力大幅减弱。由图9可以看出：当固相质量分数为60%时，球阀的流量系数变化范围为0.4～0.5，受压力波动的影响，流量系数随阀球偏移的变化与压降呈相反趋势，在 h= 5 mm，s/h=0.8时流量系数降至最小，流通能力较弱，固相颗粒有可能卡在窄阀隙内，但随着阀球开启高度的增加，流量系数基本呈增加趋势。

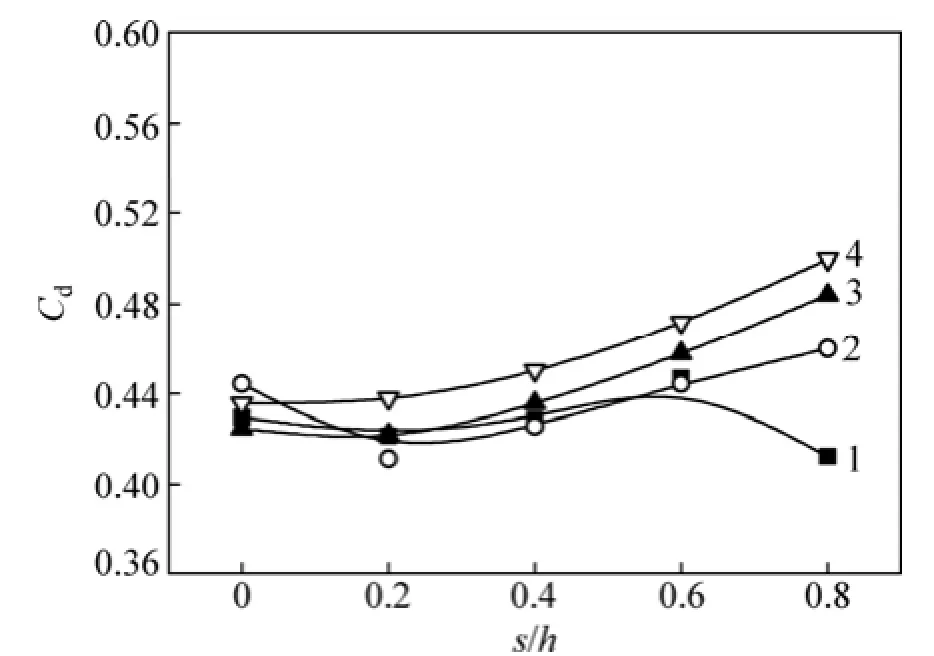
图9　各阀球开启高度下球阀流量系数随径向偏移的变化Fig. 9　Changes of flow coefficient with ball’s radial displacement under different value’s opening heights

图 10所示为在不同固相质量分数下球阀半开和全开时流量系数随径向偏移的变化规律。固定阀球径向偏移量，2种阀球开启高度下流量系数随固相质量分数均呈单调递减的趋势，数值由0.70变化至0.38。在4种固相质量分数下，阀球径向偏移距离越大， h= 9 mm时的流量系数在偏移距离为0.2～0.4时达到极小值，而 h=17 mm时的流量系数越大，阀门流通能力增强。

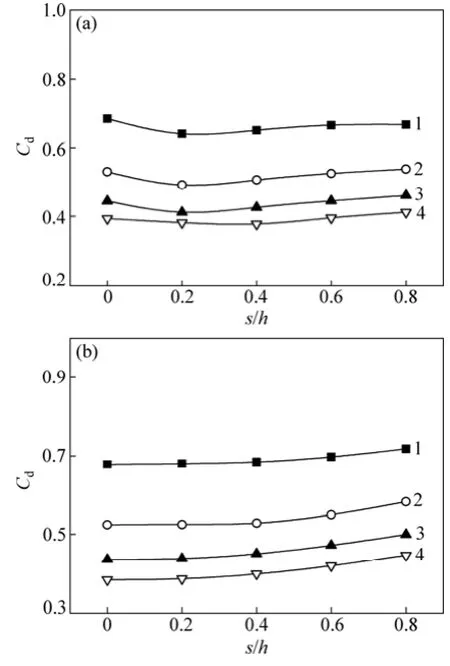
图10　不同固相质量分数下流量系数随径向偏移的变化Fig. 10 Changes of flow coefficient with ball’s radial displacement under different solid mass fractions

5　结论

1） 球阀非轴对称流场内偏移侧射流速度达到了无偏移阀隙速度的2.25倍以上，偏移相反侧二次流严重，固相颗粒贴壁流现象减弱。

2） 阀球所受作用力与进出口压降随阀球径向偏移的变化规律较为相似，当固相质量分数为60%、阀球h≤13 mm时作用力均存在一极小值点，当阀球开启高度h=17 mm时，呈单调递减趋势；不同阀球开启高度下阀球径向偏移对径向作用力的影响较之固相质量分数更为显著，会造成阀球升降程运动曲线存在瞬时较大波动。

3） 固相质量分数由20%增至80%时，球阀的流量系数变化范围为0.38～0.70，全开状态下增大阀球径向偏移距离能一定程度上增强球阀的流通能力，有利于往复泵内液固两相流的顺利排出。

［1］ WIECHMANN F， BÜCHEN K G. Piston diaphragm pumps for handling sludge and sediment［J］. World Pumps， 2006， 476（5）： 36，38-40， 42.

［2］ 全国化工设备设计技术中心站机泵技术委员会. 工业泵选用手册［M］. 2版. 北京： 化学工业出版社， 2011： 170-173. Pump Technology Committee of National Technology Center of Process Equipment. Industrial pump selection manual［M］. 2nd ed. Beijing： Chemistry Industry Press， 2011： 170-173.

［3］ ALVES M V C， BARBOSA J R， PRATA A T， et al. Fluid flow in a screw pump oil supply system for reciprocating compressors［J］. International Journal of Refrigeration， 2011， 34（1）： 74-83.

［4］ KAJIWARA S. Effect of the check ball and inlet position on hydraulic L-shaped check ball behavior［J］. Journal of Fluids and Structures， 2014， 48（7）： 497-506.

［5］ VALDÉS J R， RODRÍGUEZ J M， MONGE R， et al. Numerical simulation and experimental validation of the cavitating flow through a ball check valve［J］. Energy Conversion and Management， 2014， 78（1）： 776-786.

［6］ ROGULA J. The influence of seat fatigue test on the leakage in ball valve［C］//XIIIth International Scientific and Engineering Conference on Hermetic Sealing， Vibration Reliability and Ecological Safety of Pump and Compressor Machinery. Sumy，Ukraine： Curran Associates， Inc， 2011： 91-97.

［7］ CHERN M， WANG C， MA C. Performance test and flow visualization of ball valve［J］. Experimental Thermal and Fluid Science， 2007， 31（6）： 505-512.

［8］ YE Yi， YIN Chenbo， LI Xingdong， et al. Effects of groove shape of notch on the flow characteristics of spool valve［J］. Energy Conversion and Management， 2014， 86（10）： 1091-1101.

［9］ ZHU Hongjun， PAN Qian， ZHANG Wenli， et al. CFD simulations of flow erosion and flow-induced deformation of needle valve： effects of operation， structure and fluid parameters［J］. Nuclear Engineering and Design， 2014， 273（1）：396-411.

［10］ DEMPSTER W， ELMAYYAH W. Two phase discharge flow prediction in safety valves［J］. International Journal of Pressure Vessels and Piping， 2013， 110（10）： 61-65.

［11］ YONEZAWA K， OGAWA R， OGI K， et al. Flow-induced vibration of a steam control valve［J］. Journal of Fluids and Structures， 2012， 35（11）： 76-88.

［12］ AL-SHARIF S F， COTTON M A， CRAFT T J. Reynolds stress transport models in unsteady and non-equilibrium turbulent flows［J］. International Journal of Heat and Fluid Flow， 2010，31（3）： 401-408.

［13］ LUO Kun， WU Fan， YANG Shiliang， et al. High-fidelity simulation of the 3-D full-loop gas-solid flow characteristics in the circulating fluidized bed［J］. Chemical Engineering Science，2015， 123（2）： 22-38.

［14］ SAIDI M S， RISMANIANA M， MONJEZI M， et al. Comparison between Lagrangian and Eulerian approaches in predicting motion of micron-sized particles in laminar flows［J］. Atmospheric Environment， 2014， 89（6）： 199-206.

［15］ SAHOO P， SAHOO A. Hydrodynamic studies on fluidization of red mud： CFD simulation［J］. Advanced Powder Technology，2014， 25（6）： 1699-1708.

［16］ JEONG W， SEONG J. Comparison of effects on technical variances of computational fluid dynamics （CFD） software based on finite element and finite volume methods［J］. International Journal of Mechanical Sciences， 2014， 78（1）： 19-26.

［17］ 邵森寅. 插装式顺序阀及背压单向阀动态特性的研究［D］. 杭州：浙江大学机械与能源工程学院， 2008： 66-69. SHAO Senyin. Research on dynamic characteristics of cartridged sequence valve&cartridged check valve［D］. Hangzhou： Zhejiang University. School of Mechanical and Energy Engineering， 2008： 66-69.

［18］ SONG X， PARK Y， PARK J. Blowdown prediction of a conventional pressure relief valve with a simplified dynamic model［J］. Mathematical and Computer Modelling， 2013， 57（1/2）：279-288.

［19］ 吴金波， 陈飞， 徐礼林. 斜进口流道滑阀稳态液动力的仿真与分析［J］. 华中科技大学学报（自然科学版）， 2011， 39（11）：109-111. WU Jinbo， CHEN Fei， XU Lilin. Steady-state flow force simulation and analysis of oblique-inlet spool valves［J］. Journal of Huazhong University of Science & Technology（Natural Science Edition）， 2011， 39（11）： 109-111.

［20］ 朱万胜， 张作龙， 李继志. 钻井液提升阀流量系数的测定［J］.中国石油大学学报（自然科学版）， 2010， 34（2）： 125-129. ZHU Wansheng， ZHANG Zuolong， LI Jizhi. Measurement of flow coefficient of poppet valve for drilling fluid［J］. Journal of China University of Petroleum （Edition of Natural Sciences），2010， 34（2）： 125-129.

（编辑 刘锦伟）

Influence of radial displacement on liquid-solid two-phase flow field and characteristics in ball valve

MA Yi1， 2， ZHANG Shengchang1， 2， MA Zhongqiang1， DENG Hongying1， 2， ZHANG Zhihong1

（1. Institute of Process Equipment and Control Engineering， Zhejiang University of Technology， Hangzhou 310014， China；2. Engineering Research Center of Process Equipment and Remanufacturing，Ministry of Education， Hangzhou 310014， China）

Based on the dynamics analysis of ball’s motion， the discharge ball valve was studied as the key component of liquid-solid reciprocating pump by CFD numerical simulation. The impacts of ball’s radial displacement on two-phase flow inside the ball valve were analyzed， and the distributions of volume fraction and pressure field were predicted. Therefore， the changes of flow forces and characteristics with ball’s radial displacement were obtained at different valve’s opening heights and solid mass fractions. The results show that the secondary vortex is aggravated and the solid particles show hump-like distribution partially in the opposite side of ball’s radial displacement. The changes of forces on the ball with radial displacement are similar to those of pressure drop inside the valve， and in the order of significant effect on the radial component of forces， the factors are opening height， radial displacement， solid mass fraction successively. On the other hand， the flow coefficients range from 0.38 to 0.70 as the solid mass fractions grow from 20% to 80%， and the flow capacity has slight fluctuations with ball’s radial displacement.

ball valve； two-phase flow； concentration field； flow dynamic force； flow coefficient

TV732.7

A

1672-7207（2016）04-1158-08

10.11817/j.issn.1672-7207.2016.04.011

2015-04-17；

2015-05-30

国家自然科学基金资助项目（51406183）；浙江省自然科学基金资助项目（LY12E05023）；浙江省教育厅科研项目资助（Y201329551）（Project （51406183） supported by the National Natural Science Foundation of China； Project（LY12E05023） supported by the Natural Science Foundation of Zhejiang Province； Project （Y201329551） supported by the Educational Commission of Zhejiang Province）

马艺，博士，讲师，从事多相流泵阀理论及技术开发研究；E-mail：myant@zjut.edu.cn