铸造TiAl合金疲劳寿命统计分布

万文娟，　韩　波，　韩　伟，　张　继

(1.钢铁研究总院 高温合金新材料北京市重点实验室， 北京 100081； 2.钢铁研究总院， 北京 100081)



铸造TiAl合金疲劳寿命统计分布

万文娟1，韩波2，韩伟2，张继1

(1.钢铁研究总院 高温合金新材料北京市重点实验室， 北京 100081； 2.钢铁研究总院， 北京 100081)

对铸造Ti-47.5Al-2.5V-1.0Cr-0.2Zr(原子分数/%)合金层片组织进行了疲劳测试，获得了单一应力下的疲劳寿命数据，通过断口观察和数据统计处理，分析了疲劳寿命的分布特点及其控制因素。结果表明：实验合金的疲劳寿命具有显著波动，波动范围为103～106周；并集中分布在长、短两个寿命区间内。这一现象和导致疲劳试样失效的疲劳裂纹源的类型有关；其中，短寿命试样的疲劳裂纹起源于疏松孔洞，长寿命试样的疲劳裂纹源为弥合界面和软取向层片界面。建立了三种裂纹源对疲劳寿命的影响的两参数威布尔分布模型，可进行对应于某一失效概率的疲劳寿命预测。三种疲劳裂纹源中，疏松孔洞对疲劳寿命不利影响的程度最为严重。

TiAl合金；疲劳寿命；铸造缺陷；威布尔分布

TiAl合金具有较高的高温比强度和良好的抗蠕变和抗氧化性能，是一种颇具应用潜力的新型轻质高温结构材料，用于高温下工作的转动件尤其具有优势。如GE公司发动机在GEnx低压涡轮后两级叶片采用TiAl合金，为实现该航空发动机的高效率、低油耗设计目标发挥了重要作用[1-2]。

TiAl合金层片组织微观上力学性能具有较大的各向异性，其中疲劳裂纹的萌生和扩展的抗力是随机的，由此导致疲劳寿命表现出明显的分散性[3-6]。而疲劳寿命的分散性是工程结构设计、特别是转动件设计必须考虑的因素，揭示疲劳寿命的统计分布规律及其控制因素是建立结构件疲劳寿命预测模型的必要条件。

Jha等研究了Ti-48Al-2Mn-2Nb(原子分数/%)+2TiB2(质量分数/%)合金等轴层片组织在相同实验条件下的疲劳寿命波动性，认为组织中等轴层片团的随机分布所导致的表面形核和亚表面形核两种失效机制的竞争才是造成寿命大幅波动的根本原因，其应力-寿命关系也应采用双重机制进行描述[3-4]。然而，对于其他非等轴层片组织TiAl合金而言，其疲劳寿命分散性控制因素及寿命统计分布规律仍有待研究。

本工作采用旋转弯曲的加载方式，对含有单一取向层片组织[7-9]的铸造Ti-47.5Al-2.5V-1.0Cr-0.2Zr(原子分数/%)合金进行了高温疲劳性能测试，分析了单一应力下的疲劳寿命分布特点，并通过断口观察和采用统计分布方法分析讨论了导致疲劳寿命这一分布特点的原因。

1　实验材料与方法

采用离心铸造工艺获得尺寸为100 mm×70 mm×10 mm的板状Ti-47.5Al-2.5V-1.0Cr-0.2 Zr(原子分数/%)铸锭。在1270 ℃/180 MPa/Ar/1.5 h条件下对板状铸锭进行热等静压处理后，为稳定组织，对铸锭进行950 ℃/12 h真空退火处理并炉冷至室温。

沿板状铸锭宽度方向切取试样，研磨和抛光后，采用OLYMPUS GX71金相显微镜和JEOL JSM-6480LV扫描电镜观察铸锭横截面缺陷分布情况。之后选用3%HF+24%HNO3+23%H2O+50%丙三醇 (体积分数)溶液对抛光态试样进行腐蚀，利用金相显微镜进行显微组织观察。

沿板状铸锭宽度方向掏取圆棒，机加工后获得沙漏型光滑疲劳试样(试样长52 mm，中心位置直径为4 mm)，试样的轴向平行于板状铸锭的宽度方向。为减少试样表面状态对疲劳性能的影响，采用2000#SiC砂纸沿轴向对疲劳试样表面进行抛光。

2　结果与分析

2.1组织观察

对板状铸锭横截面的金相试样进行观察，其宏观组织为由铸锭表面向内整齐对长的柱状晶组织，柱状晶宽度约90～360 μm，柱状晶生长方向垂直于铸锭表面和宽度方向，在最后凝固线上离散分布有尺寸不同的等轴层片团(50～2000 μm)，如图1(a)所示。微观上，柱状晶区全为γ-TiAl/α2-Ti3Al两相层片组织(见图1(b))，且γ/α2层片界面垂直于柱状晶生长方向，因而，层片界面也平行于铸锭表面和宽度方向，试样内层片组织具有整体一致取向。离散分布在最终凝固线上的极少量等轴层片团中，层片取向随机，与柱状晶中层片取向差异较大，如图1(c)所示。

观察试样抛光面发现，在板状铸锭横截面上，在距试样中轴线约2 mm的区域范围内分布有孔洞缺陷，在其他区域分布较少。其中多数是形状不规则的显微疏松，如图2(a)所示，气孔较少。除孔洞缺陷外，还观察到一种由孔洞缺陷经热等静压处理转变而成的弥合界面缺陷，一般为粗糙曲面，如图2(b)中所示。在热等静压处理过程中，由于高温高压作用，孔洞缺陷周围区域发生变形，导致部分孔洞虽崩塌压合，但其内表面却未能相互结合完全致密化，从而产生界面型的残留缺陷。

图1　板状铸锭横截面金相组织　(a)柱状晶组织(等轴层片团如箭头所示)；(b)γ/α2层片组织；(c)等轴层片团Fig. 1　　　　Microstructures of the cross section of the plate-like ingot　(a)columnar grains (an equiaxed colony as indicated by the arrow);(b)γ/α2 lamellar microstructure; (c)the equiaxed colony

图2　板状铸锭横截面上观察到的缺陷　(a)疏松孔洞；(b)弥合界面Fig.2　Defects observed on the cross section of the plate-like ingot　(a)shrinkage porosity;(b)bridged porosity interface

2.2疲劳寿命分布和断口分析

实验合金疲劳试样在给定条件下的疲劳测试结果见应力-寿命散点图(图3)。如图所示，疲劳寿命数据表现出较大的分散性，寿命最小值Nfmin和最大值Nfmax分别是3.48×103周和5.71×106周，两者之间相差三个数量级。并且，疲劳寿命主要分布在两个区间：一是短寿命区间，即3.48×103～1.96×104周，对应试样占总试样数量的比例为42.5%；二是长寿命区间，即6.32×105～5.71×106周，占比55%。

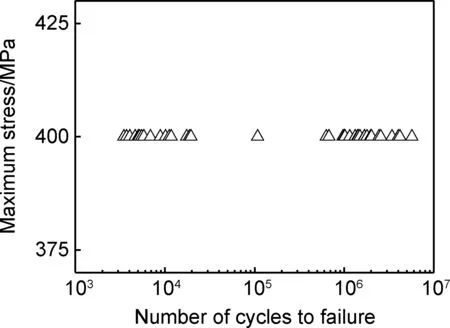
图3　　　　Ti-47.5Al-2.5V-1.0Cr-0.2Zr铸造合金层片组织的750 ℃疲劳测试结果Fig. 3　　　　Fatigue test results of Ti-47.5Al-2.5V-1.0Cr-0.2Zr cast alloy with lamellar microstructure tested at 750 ℃

Ti-48Al-2Mn-2Nb(原子分数/%)+2TiB2(质量分数/%)合金等轴层片组织在σmax=475 MPa，600 ℃和R=0.1的实验条件下得到的疲劳寿命为2.5×103～1.2×107周，同样具有大幅波动[3]。与之相比，实验合金在给定条件下的疲劳寿命波动范围稍小，但仍高达三个数量级。两种合金的疲劳寿命分布特点相似，均集中在短寿命区和长寿命区两个区间内。对于等轴层片组织，合金中层片团取向的随机分布是导致疲劳寿命产生明显波动的重要原因。层片团取向的随机分布导致软取向层片团(如层片界面和外加载荷方向的夹角约45°[11])出现位置和概率随机，从而产生了两种疲劳裂纹形核方式：表面裂纹形核和亚表面裂纹形核，二者对应的萌生抗力和萌生寿命具有显著差异。由于TiAl合金对长裂纹扩展的阻力较低[12]，其疲劳寿命主要取决于疲劳裂纹萌生阶段，导致两种失效机制对应试样的疲劳寿命分别集中分布在短寿命区间和长寿命区间[13]。

然而，对于实验合金而言，其组织中层片取向一致，其组织中并不存在大量取向随机的层片团。并且，其层片界面平行于外加应力，处于硬取向，为择优取向层片组织；因此，实验合金疲劳寿命大幅波动的原因与等轴层片组织合金中寿命波动的原因并不相同。对实验合金疲劳试样进行了断口观察，通过对比短寿命和长寿命试样的断口形貌进行分析。

断口观察发现，在图3中所测试的试样中，所有断口均具有一致的宏观形貌，断面整体较平整，并与外加应力方向垂直。断口周围无明显宏观塑性变形，表现出脆性断裂特征。断口具有明显低应力高周疲劳断裂特征，可分为三个区域：疲劳源、裂纹扩展区(疲劳区)和瞬时断裂区(瞬断区)，如图4，分别对应于疲劳破坏过程的三个阶段，即疲劳裂纹萌生、疲劳裂纹扩展和失稳断裂阶段。

图4　疲劳断口宏观形貌A：疲劳源，B：疲劳区，C：瞬断区Fig.4　　　　Macroscopic fracture morphology of a fatigue specimen,A: crack initiation, B: crack propagation and C: final fracture

与等轴层片组织疲劳断口上明显不同的是，实验合金所有试样的疲劳裂纹均萌生自在循环加载过程中承受最大应力的表面层，无亚表面或试样内部裂纹萌生。因而，等轴层片组织中的双重裂纹形核失效机制无法解释实验合金的寿命波动和长短寿命分区现象。

对于实验合金，短寿命和长寿命试样断口特征的明显区别在于，二者的疲劳源类型完全不同。短寿命试样的疲劳裂纹源均为大尺寸(140～890 μm)的疏松孔洞，如图5(a)，在应力集中系数更大的孔洞尖角处易萌生裂纹。多数试样的疲劳裂纹自单一裂纹源萌生和扩展，仅在两个试样断面上观察到双裂纹源。对于长寿命试样，其疲劳裂纹源均具界面型特征，可分为弥合界面和软取向层片界面两种类型，分别见图5(b)和(c)。其中，多数试样为弥合界面(60～140 μm)裂纹起源，仅有少数试样的疲劳裂纹萌生自等轴层片团的软取向层片界面(120～240 μm)。弥合界面裂纹源处呈现出明显不同于周围层片组织的粗糙沟壑状特征，这是由于压合面未致密化导致的。疲劳裂纹沿软取向层片界面萌生时，疲劳源处具有平行层叠的光滑沿层特征。

统计不同类型疲劳裂纹源对应的疲劳试样的数量发现，大部分试样的疲劳裂纹萌生于疏松孔洞和弥合界面，二者在所有40个试样中所占比例均为42.5%；而疲劳裂纹萌生于等轴层片团的软取向层片界面的试样仅占15%。

疲劳裂纹萌生后，以裂纹源为中心、沿多条路径向试样内部辐射状扩展，源区周围区域由于疲劳过程中的挤压摩擦而较为平滑，呈现出小的、较平坦的半圆形裂纹扩展区，如图4所示。

对于实验合金试样而言，虽寿命长短不同，但疲劳裂纹扩展区的特征相似。在疲劳裂纹扩展区可见明显穿层片扩展特征，如图6(a)所示。在裂纹穿层片扩展过程中，可观察到层片的微观塑性变形特征：穿层片且与层片成一定角度的平行线状显微滑移和/或显微孪生痕迹(见图6(b))，以及解理河流花样和二次裂纹。沿主裂纹的扩展路径未见孔洞缺陷或弥合界面，仅在一个短寿命试样裂纹扩展区观察到由于软取向层片界面而导致的穿层片和沿层片界面交替的台阶式扩展断面，如图6(c)所示。这意味着，在裂纹扩展过程中，软取向层片界面对主裂纹扩展方向有一定影响，而孔洞缺陷和弥合界面并非是影响裂纹稳态扩展的主要因素。当裂纹扩展至线弹性断裂尺度时，长裂纹快速扩展直至发生断裂。瞬断区断面粗糙，具有明显穿层片断裂特征，并发生大量层间开裂，形成沿层片界面二次裂纹。

由断口观察结果可知，短寿命和长寿命试样的疲劳裂纹源类型和尺寸明显不同，短寿命试样的裂纹源为疏松孔洞(140～890 μm)，而长寿命试样的裂纹源为弥合界面(60～140 μm)和软取向层片界面(120～240 μm)。而在疲劳裂纹扩展区以及瞬断区，不同寿命的试样的裂纹扩展特征相似，均为穿层片断裂。因而，实验合金的疲劳寿命大幅波动是由于引起失效的疲劳裂纹源的不同所导致的。疲劳源类型和尺寸不同、导致疲劳裂纹萌生抗力和萌生寿命不同，由于TiAl合金疲劳寿命主要取决于裂纹萌生阶段，因而对实验合金的疲劳寿命产生了不同程度的影响，导致疲劳寿命出现大幅波动。

图5　典型疲劳裂纹源特征　(a)疏松孔洞；(b)弥合界面；(c)软取向层片界面Fig.5　　　　Typical characteristics of fatigue crack initiators　(a)shrinkage porosity；(b)bridged porosity;(c)soft-oriented lamellar interface

图6　疲劳裂纹扩展特征　(a)裂纹穿层片扩展；(b)显微滑移和/或孪生痕迹；(c)台阶式裂纹扩展Fig.6　　　　Characteristics of fatigue crack propagation　(a)translamellar crack propagation;(b)deformation traces caused by microslipand microtwinning;(c)step-like crack propagation

2.3疲劳寿命统计分布

研究发现，实验合金疲劳寿命大的分散性对应的是不同类型疲劳裂纹源的问题，因而，可采用威布尔分布对实验合金在同一测试条件下所获得的疲劳寿命数据进行分析。威布尔分布是瑞典物理学家Waloddi Weibull分析材料强度时在实际经验的基础上推导出来的分布形式[13]，能充分反映材料缺陷和应力集中源对材料疲劳寿命的影响，并且适用于小样本抽样。

在某一应力水平下，若疲劳试样的疲劳寿命Nf服从威布尔分布，则疲劳寿命的三参数威布尔分布函数为：

(1)

式中：F(Nf)是疲劳试样在低于或等于给定周次Nf时发生失效的统计概率；N0是位置参数，即最小寿命参数，表示试样在N0之前不会失效；Na是特征寿命参数，当Nf=Na时，F(Nf)=0.632；m为形状参数，又称威布尔系数。

当N0=0时，三参数威布尔分布退化为二参数威布尔分布，疲劳寿命的分布函数为：

(2)

在二参数威布尔分布中，常采用线性回归法、矩量法和极大似然法分析疲劳寿命数据[14]，以估算特征寿命参数Na和形状参数m。在本研究中，将采用线性回归法估算两个参数。

在一组总数为n的疲劳试样的寿命数据中，根据试样对应的寿命长短从小到大排列试样，则其中第i个试样失效时的累计失效概率F(Nfi) 可用中位秩算法[14]求得：

(3)

对(2)式做变形处理，并取两次自然对数，可得：

(4)

根据式(4)，可对疲劳寿命数据进行线性回归，求出Na和m，并获得相关系数r，该值越大说明数据点与所获直线匹配度越高。如果数据点明显是非线性的或相关系数值太低，说明二参数威布尔分布并不能很好地描述实验合金的疲劳寿命数据。

图7中显示，在σmax=400 MPa,R=-1和750 ℃的测试条件下，在实验合金疲劳寿命数据的两参数威布尔分布曲线中，试样的疲劳失效概率F(Nf)是疲劳寿命Nf的函数。对于因疏松孔洞、弥合界面或软取向层片界面失效的各组试样，其疲劳数据点都是线性的。这意味着，图7中的疲劳寿命数据的两参数威布尔分布可以很好地描述三组不同疲劳裂纹源失效试样的疲劳失效行为，解释了实验合金疲劳寿命的明显波动和分区分布行为。

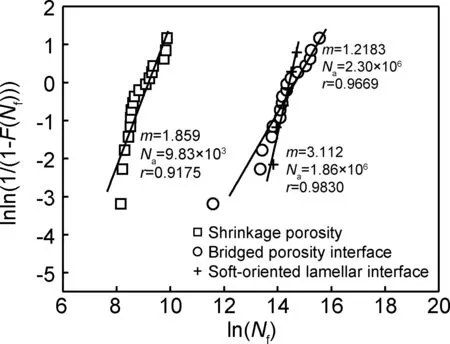
图7　　　　Ti-47.5Al-2.5V-1.0Cr-0.2Zr铸造合金层片组织疲劳寿命数据的两参数威布尔分布曲线Fig. 7　　　　Two-parameter Weibull plot for fatigue life data of Ti-47.5Al-2.5V-1.0Cr-0.2Zr cast alloy with lamellarmicrostructure

图7中的曲线特征表明了疲劳裂纹源对疲劳寿命的影响特点。其中，三维形态的疏松孔洞对疲劳寿命的影响最为不利，它对疲劳寿命的影响程度显著高于二维形态的弥合界面和软取向层片界面，从而导致对应试样的疲劳寿命位于图3中的短寿命区。在循环应力作用下，三维孔洞的存在会导致其周围基体应力集中。对于给定尺寸孔洞缺陷，如果缺陷位于自由表面而非试样内部，那么，所对应的应力强度因子将高出55%[15]。而实验合金试样中的孔洞裂纹源均位于试样表面层，因而，其周围区域的高度应力集中加速了疲劳裂纹的萌生。

弥合界面和软取向层片界面对疲劳寿命的影响程度比较接近，这和二者均为二维形态有关。如图7所示，两种界面型疲劳源对疲劳寿命的影响程度均明显低于三维形态的疏松孔洞，使对应的疲劳寿命提高了2～3个数量级，对应于图3中的长寿命区；不过，虽形态类似，但二者本质并不同，因而对疲劳寿命的影响程度也有差异。弥合界面是孔洞缺陷经热等静压后得到的压合面，并无冶金结合，在外力作用下易起到初始裂纹的作用。而软取向层片界面是冶金结合面，只是由于和外力的相对取向不利(如二者夹角为约45°)，易发生微观塑性变形，从而导致沿该弱结合面萌生裂纹。图7中也显示，两种裂纹源对应的回归直线有交点。在ln(Nf)低于交点值时，弥合界面对疲劳寿命的影响程度较软取向层片界面稍大；反之，则软取向层片界面对疲劳寿命影响程度更大。

疏松孔洞失效试样的威布尔系数m是1.859，其特征疲劳寿命Na为9.83×103周。这一线性回归模型还可用于预测对应某一失效概率的疲劳寿命，如，失效概率为0.1%时，对应疲劳寿命为2.39×102周。弥合界面失效试样的威布尔系数m为1.2183，其特征疲劳寿命Na是2.30×106周；当失效概率为 0.1%时，对应疲劳寿命为7.94×103周。对于软取向层片界面失效试样，其威布尔系数m为3.112，其特征疲劳寿命是1.86×106周；失效概率为0.1%时所对应的疲劳寿命为2.02×105周。在三种疲劳源对应的疲劳寿命分布模型中，软取向层片界面对应的威布尔系数最高，即疲劳寿命分散程度最低；弥合界面裂纹源的威布尔系数最低，疲劳寿命数据分散程度最高。

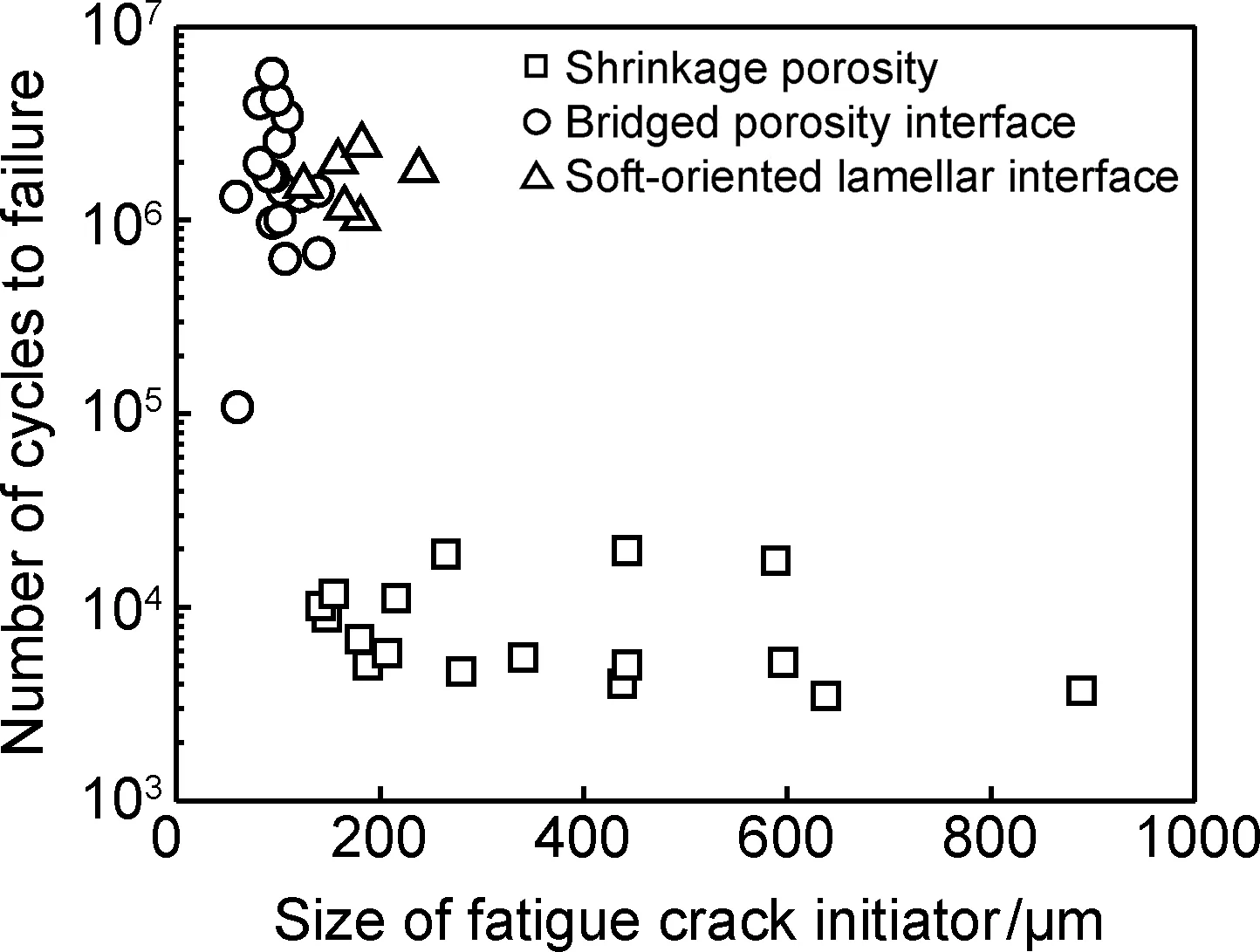
图8　　　　Ti-47.5Al-2.5V-1.0Cr-0.2Zr合金疲劳寿命和裂纹源尺寸之间的关系Fig. 8　　　　Relationship between fatigue life and crack initiator size of Ti-47.5Al-2.5V-1.0Cr-0.2Zr alloy

从实验合金疲劳寿命的两参数威布尔分布结果可知，疲劳寿命的大幅波动和集中分布在长短两个寿命区的现象，是因为疲劳裂纹源的性质不同导致的。疏松孔洞裂纹萌生失效机制对应着短寿命区间，弥合界面和软取向层片界面裂纹萌生两种失效机制对应长寿命区间。不过，在任一寿命区间内，疲劳寿命仍有约一个数量级的波动。在短寿命区中，这一小幅波动可能是由于孔洞缺陷尺寸不同所导致的，如图8所示，虽然并不严格符合，但从整体而言，仍表现出疲劳寿命随疏松孔洞裂纹源尺寸增大而降低的趋势。而在长寿命区内，疲劳源尺寸和疲劳寿命之间却并未见明显规律。不过，当对应的疲劳寿命接近时，软取向层片界面的尺寸大于弥合界面的尺寸。这说明，若二者尺寸接近，弥合界面对疲劳寿命的影响程度更大、对应的疲劳寿命更低。

基于上述结果和分析，减少合金中的缺陷和等轴层片团的数量以及缩小其尺寸对推迟疲劳裂纹萌生是有利的，进而有助于减轻对疲劳寿命的不利作用和减小疲劳寿命的波动幅度。对于实验合金而言，铸造缺陷(疏松孔洞和弥合界面)作为疲劳裂纹源的试样占总数比例高达85%，因而，可通过优化铸造工艺和调整热等静压处理工艺、减少铸造缺陷的数量和尺寸来实现提高疲劳寿命、减轻疲劳寿命波动这一目标。

3　结论

(1)铸造Ti-47.5Al-2.5V-1.0Cr-0.2Zr (原子分数/%)合金试样在750 ℃,σmax=400 MPa(R=-1)条件下，在单一应力作用下，疲劳寿命具有明显波动，波动幅度高达三个数量级。疲劳寿命主要集中分布在两个区间内，即短寿命区103～104周和长寿命区105～106周。

(2)所有疲劳试样均以表面裂纹起源方式发生失效。疲劳寿命的大幅波动是由于导致试样失效的疲劳裂纹源类型不同：短寿命试样的疲劳裂纹起源于疏松孔洞，长寿命试样的疲劳裂纹则萌生自弥合界面和软取向层片界面。同类型裂纹源失效试样的疲劳寿命差别较小，导致寿命集中分布。

(3)定应力下，三种疲劳裂纹源对实验合金疲劳寿命的影响规律可采用两参数威布尔分布模型进行描述。疏松孔洞、弥合界面和软取向层片界面对应的威布尔系数m分别为1.859,1.2183和3.112，特征疲劳寿命Na分别为9.83×103周、2.30×106周和1.86×106周。这一线性回归模型可用于预测对应某一失效概率的疲劳寿命。

[1] KIM Y W，DIMIDUK D M．Progress in the understanding of gamma titanium aluminides[J]．JOM，1991，43(8)：40-47．

[2] KIM Y W．Gamma titanium aluminides：their status and future[J]．JOM，1995，47(7)：39-42．

[3] JHA S K，LARSEN J M，ROSENBERGER A H．The role of competing mechanisms in the fatigue life variability of a nearly fully-lamellar γ-TiAl based alloy[J]．Acta Materialia，2005，53：1293-1304．

[4] JHA S K，LARSEN J M，ROSENBERGER A H．The role of competing mechanisms in the fatigue-life variability of a titanium and gamma-TiAl alloy[J]．JOM，2005，57(9)：50-54．

[5] TRAIL S J，BOWEN P．Effects of stress concentrations on the fatigue life of a gamma-based titanium aluminide[J]．Materials Science and Engineering A，1995，192/193 (Part 1)：427-434．

[6] ZHOU Y，WANG J Q，ZHANG B，etal．High-temperature fatigue property of Ti46Al8Nb alloy with the fully lamellar microstructure[J]．Intermetallics，2012，24：7-14．

[7] 张继，仲增镛．TiAl金属间化合物工程实用化研究与进展[J]．中国材料进展，2010，29(2)： 9-13．

(ZHANG J，ZHONG Z Y．Research and development of TiAl intermetallics-based alloys[J]．Materials China，2010，29(2)：9-13．)

[8] 张继，张志宏，邹敦叙，等．铸造钛铝合金组织与力学性能[J]．航空材料学报，1998，18(3)：29-33．

(ZHANG J，ZHANG Z H，ZOU D X，etal．Microstructures and mechanical properties of cast TiAl alloys[J]．Journal of Aeronautical Materials，1998，18(3)：29-33．)

[9] 张继，张建伟，邹敦叙，等．TiAl合金铸态组织γ/α2层片排列取向设计[J]．高技术通讯，1997(3)： 4-7．

(ZHANG J，ZHANG J W，ZOU D X，etal．Design of γ/α2lamellar orientation in cast TiAl alloy microstructures[J]．High Technology Letters，1997(3)：4-7．)

[10]万文娟，韩波，韩伟，等．TiAl合金择优取向层片组织的高周疲劳行为研究[J]．航空材料学报，2016，36(1)：87-92．

(WAN W J，HAN B，HAN W，etal．An investigation of high-cycle fatigue behavior of a TiAl alloy containing preferentially oriented lamellar microstructures [J]．Journal of Aeronautical Materials，2016，36(1)：87-92．)

[11]INUI H，OH M H，NAKAMURA A，etal．Room-temperature tensile deformation of polysynthetically twinned (PST) crystals of TiAl[J]．Acta Metallurgica et Materialia，1992，40(11)：3095-3104．

[12]BOWEN P，CHAVE R A，JAMES A W．Cyclic crack growth in titanium aluminides[J]．Materials Science and Engineering A，1995，192/193(Part 1)：443-456．

[13]WEIBULL W．A statistical distribution function of wide applicability[J]．Journal of Applied Mechanics，1951，18(3)：293-297．

[14]KHALILI A，KROMP K．Statistical properties of Weibull estimators [J]．Journal of Materials Science，1991，26(24)：6741-6752．

[15]WANG Q G，APELIAN D，LADOS D A．Fatigue behavior of A356-T6 aluminum cast alloys:Part I—effect of casting defects [J]．Journal of Light Metals，2001，1(1)：73-84．

Statistical Distribution of Fatigue Life for Cast TiAl Alloy

WAN Wenjuan1,HAN Bo2,HAN Wei2,ZHANG Ji1

(1．Beijing Key Laboratory of Advanced High Temperature Materials, Central Iron & Steel Research Institute, Beijing 100081, China;2．Central Iron & Steel Research Institute, Beijing 100081, China)

Statistic distribution of fatigue life data and its controls of cast Ti-47.5Al-2.5V-1.0Cr-0.2Zr (atom fraction/%) alloy were investigated. Fatigue tests were operated by means of load-controlled rotating bending fatigue tests (R=-1) performed at a frequency of 100 Hz at 750 ℃ in air. The fracture mechanism was analyzed by observing the fracture surface morphologies through scanning electron microscope，and the achieved fatigue life data were analyzed by Weibull statistics. The results show that the fatigue life data present a remarkable scatter ranging from 103to 106cycles, and distribute mainly in short and long life regime. The reason for this phenomenon is that the fatigue crack initiators are different with different specimens. The crack initiators for short-life specimens are caused by shrinkage porosity, and for long-life ones are caused by bridged porosity interface and soft-oriented lamellar interface. Based on the observation results of fracture surface, two-parameter Weibull distribution model for fatigue life data can be used for the prediction of fatigue life at a certain failure probability. It has also shown that the shrinkage porosity causes the most detrimental effect to fatigue life.

TiAl alloy; fatigue life; casting defects; Weibull statistics

(责任编辑：徐永祥)

2015-12-21；

2016-01-17

万文娟(1985—)，女，博士研究生，主要研究方向铸造TiAl合金，(E-mail)wanwenjuanwwj@126.com。

10.11868/j.issn.1005-5053.2016.4.010

TG146.2

A

1005-5053(2016)04-0071-07