基于大变形蠕变分析的持久寿命预测方法

叶文明，　胡绪腾，　马晓健，　宋迎东,3



基于大变形蠕变分析的持久寿命预测方法

叶文明1，胡绪腾1，马晓健2，宋迎东1,3

(1. 南京航空航天大学 能源动力学院 江苏省航空动力系统重点实验室， 南京 210016； 2. 中航工业沈阳发动机设计研究所 压气机研究室， 沈阳 110015； 3. 南京航空航天大学 机械结构力学及控制国家重点实验室， 南京 210016)

提出一种基于真应力真应变弹塑性蠕变本构模型和大变形有限元分析的高温构件持久寿命预测方法。该方法利用以真应力-真应变表示的材料高温拉伸应力-应变曲线建立材料的弹塑性模型，基于蠕变曲线建立蠕变本构模型，并采用大变形有限元方法计算高温构件在给定载荷下的变形响应曲线，根据其响应曲线的变化趋势来确定构件持久寿命。通过TC11钛合金缺口试件500 ℃下的持久试验对上述方法进行验证，并与三种基于小变形分析的持久寿命预测方法进行对比。结果表明：本工作提出的方法可以较准确地预测TC11缺口试件的高温蠕变响应和持久寿命，其预测精度优于基于关键点断裂应变、缺口净截面平均有效应力以及骨点应力的小变形有限元分析的寿命预测方法。

持久寿命预测；蠕变本构；TC11钛合金；缺口试件；有限元分析

长期在高温下使用的工程构件或结构，有发生持久应力断裂的风险。准确可靠的持久寿命预测方法是高温结构设计的重要基础，可保证这类工程结构的安全。

国内外学者对高温构件所用材料的蠕变持久性能进行了大量的研究[1-12]，发展出了不同的寿命预测方法。Hyde等[1]对一种镍基高温合金和一种钛合金进行蠕变研究，将骨点有效应力和最大主应力组合成为参考应力，运用持久寿命方程进行寿命预测。董露等[4]运用持久寿命方程对Ti40钛合金持久寿命进行预测，其结果置信度可达99.94%。Oh等[6]运用蠕变延性耗竭模型对316H合金500 ℃下的蠕变失效进行模拟。Liu等[8]运用有限元分析方法获得DD6镍基高温合金缺口试样最小截面上的骨点应力，并与连续介质损伤力学(CDM)结合对缺口圆棒试样的持久寿命进行预测。Huang等[9]研究镍基高温合金不同缺口类型试样的蠕变性能，发现其断裂寿命与最小蠕变应变率之间的关系受到试样约束度的影响。Goyal等[10-11]运用有限元法对两种钢的缺口试样进行分析，并结合幂函数形式的寿命方程和CDM方法进行寿命预测，发现Von Mises有效应力为9Cr-1Mo钢多轴应力蠕变断裂寿命主要的控制参量。

实际结构在发生蠕变破坏时，其内部已发生较大的变形，在进行有限元分析时不能忽略因变形导致的结构尺寸和形状的改变。上述研究基本都基于小变形有限元分析结果进行持久寿命预测。本工作提出一种基于大变形有限元分析的高温结构持久寿命预测新方法。

1　基于大变形有限元分析的持久寿命

预测方法

1.1材料的弹塑性蠕变本构模型

为准确预测高温构件在初始加载和持续静载荷作用下可能发生的大变形响应，材料的弹塑性变形和蠕变变形均要采用大变形本构模型来描述。对于弹性变形，采用广义Hooke定律来描述。对于塑性变形，可采用非线性各向同性硬化模型来描述。在单轴应力状态下，非线性硬化函数为：

σy(εpl)=σy0+R0εpl+R∞(1-e-bεpl)

(1)

式中：εpl为塑性应变；σy0为初始屈服应力；R0，R∞，b为各向同性硬化参数。上述硬化模型参数可由采用真应力-真应变表示的材料高温拉伸曲线拟合获得。

为准确预测结构的高温蠕变大变形响应，材料的蠕变变形需要采用能够描述蠕变曲线全过程的本构模型来描述。Evans等[12]提出的θ参数方程可描述三阶段蠕变曲线，单轴应力下其公式为：

εc=10a1+b1σ(1-e-t·10a2+b2σ)+

10a3+b3σ(et·10a4+b4σ-1)

(2)

式中：εc为蠕变应变；t为时间；ai,bi(i=1,2,3,4)为待定参数。蠕变模型材料参数可由采用真应力-真应变表示的材料蠕变曲线拟合获得。

1.2基于大变形有限元分析的持久寿命预测方法

针对实际结构在发生蠕变破坏时其内部往往已累积较大变形，且结构局部尺寸发生明显变化， 本工作提出采用大变形有限元分析方法计算构件在高温下的整体变形响应曲线，如图1所示。随计算时间增加构件变形量将逐渐增大，其内部危险部位变形逐渐累积，当整体变形响应因其局部蠕变变形累积到第三阶段时急剧增大，有限元计算过程将无法收敛而停止，此时可认为构件发生持久断裂破坏，根据计算结果获得构件的持久断裂寿命。

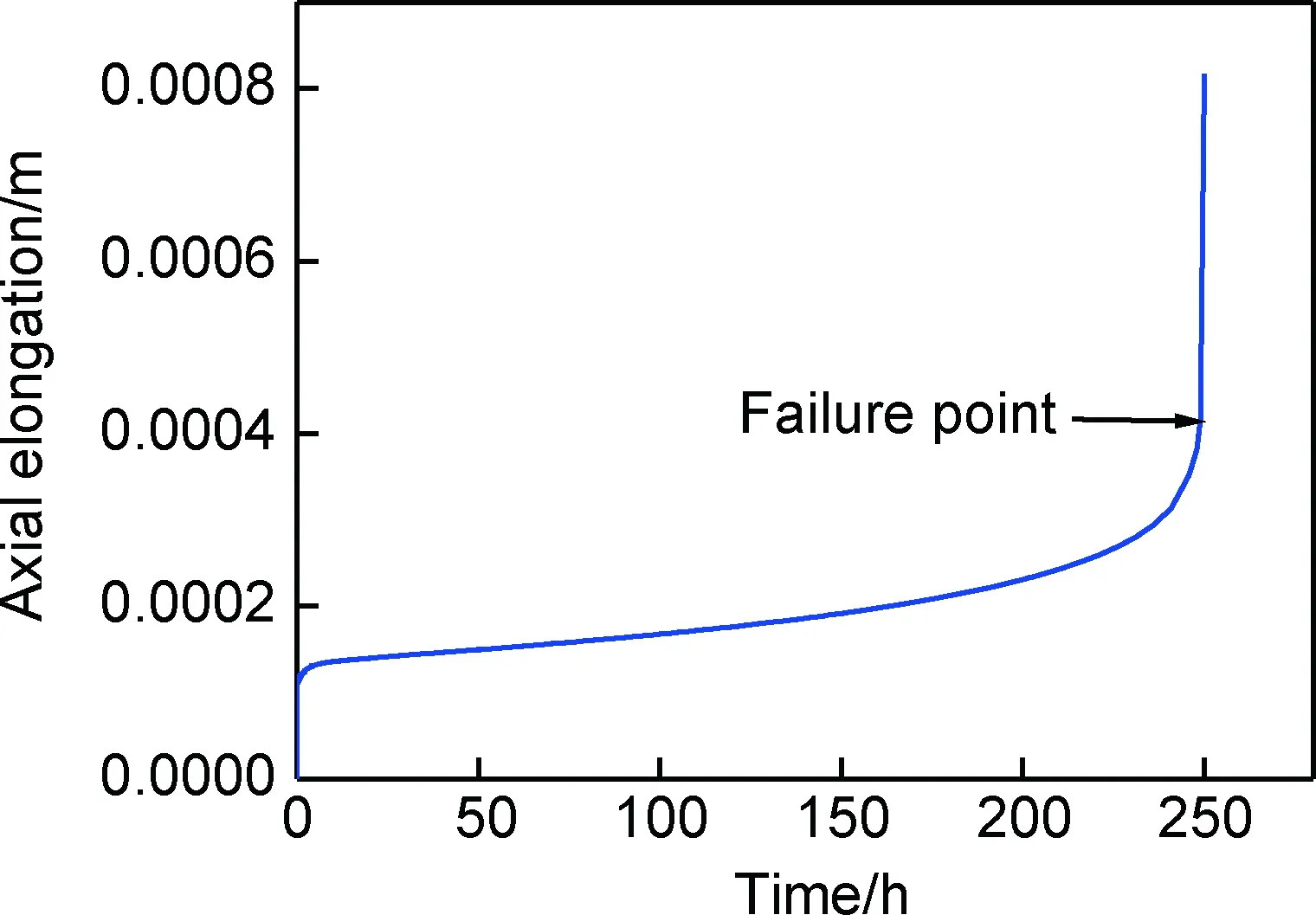
图1　构件高温下的变形响应曲线有限元计算结果示意图Fig.1　　　　Finite element calculation results of the deformation response curves at high temperature

2　TC11蠕变持久试验

2.1材料与方法

近年来，随着航空发动机技术的不断进步，其对使用材料的要求也越来越高，国外先进航空发动机中，钛合金用量已占到发动机总质量的25%～ 40%，如F100发动机约为25%，F119发动机达到40%左右。我国军用发动机的钛用量已从早期的“零” 按不同机型分别提高至10%，13%，15%和25%，正在研制的民用发动机的钛用量预期为23%左右。航空发动机使用材料的总趋势从早期的钢、铝时代转化成冷端以钛为主，热端以镍为主的镍、钛、钢“三足鼎立”的时代[13]。国内对于钛合金的高温性能进行了一定的研究[14-16]，因此本工作采用航空发动机常用材料TC11钛合金对基于大变形有限元分析的持久寿命预测方法进行实验验证。

该合金主要化学成分包括Ti，Al，Mo，Zr，Si以及Fe等元素，制造参照GJB 2220—1994进行 。为获得TC11合金的高温弹塑性本构模型，按照GB/T 4338—2006拉伸试验方法在INSTRON-5869台式电子万能材料试验机上进行500 ℃高温拉伸试验。500 ℃下的蠕变/持久试验按照GB/T2039—1997在CSS-3950电子蠕变/持久试验机上进行。

为验证本工作提出的持久寿命预测方法，选择TC11合金进行500 ℃下的持久寿命试验，并采用缺口件模拟实际结构中因几何不连续而导致其内部呈现多轴应力状态的现象。设计的三种不同缺口半径圆棒试件的缺口件形状和基本尺寸如图2和图3所示。

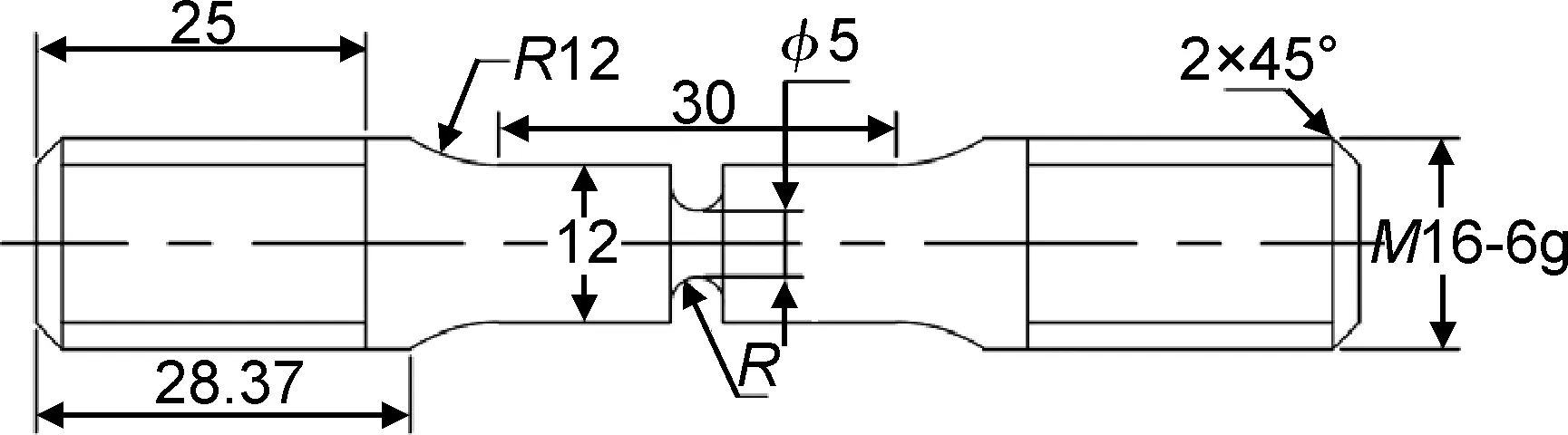
图2　缺口圆棒试样基本尺寸Fig.2　Basic sizes of notched bar specimen

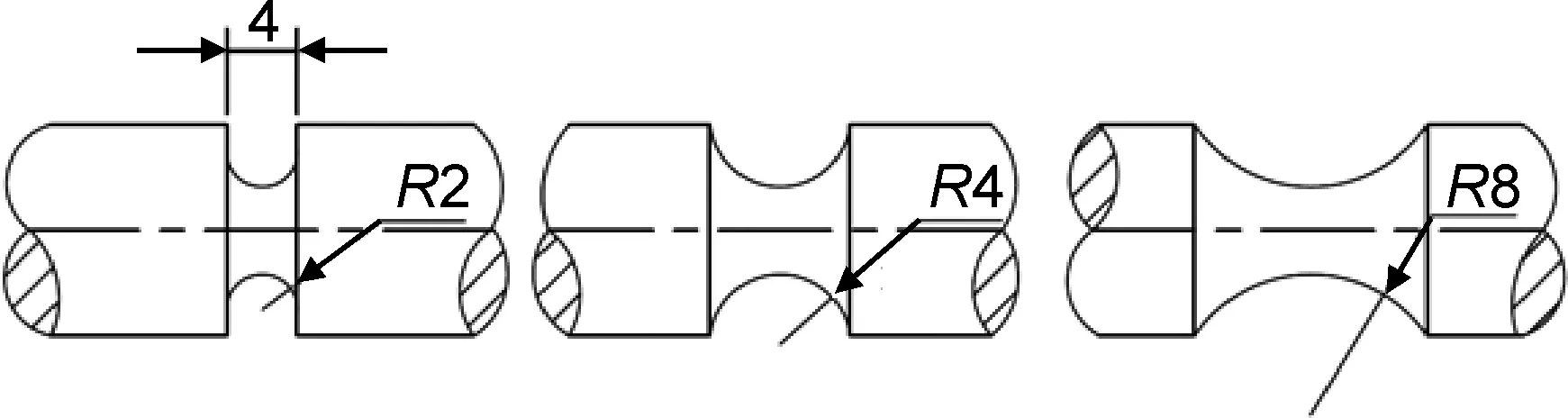
图3　缺口尺寸Fig.3　Sizes of notches

2.2试验结果

对TC11钛合金500 ℃下高温拉伸试验结果进行处理可得到其工程应力应变以及真实应力应变曲线，如图4所示。

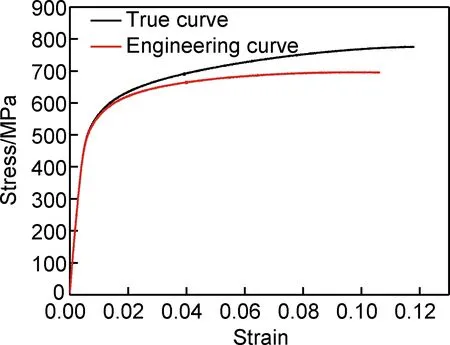
图4　TC11钛合金在500 ℃下的拉伸应力应变曲线Fig.4　　　　Tensile stress-strain curves of TC11 titanium alloy at 500 ℃

对TC11钛合金500 ℃下光滑圆棒试样蠕变性能数据进行处理后可得其真应变以及工程应变表示的蠕变曲线，如图5所示。

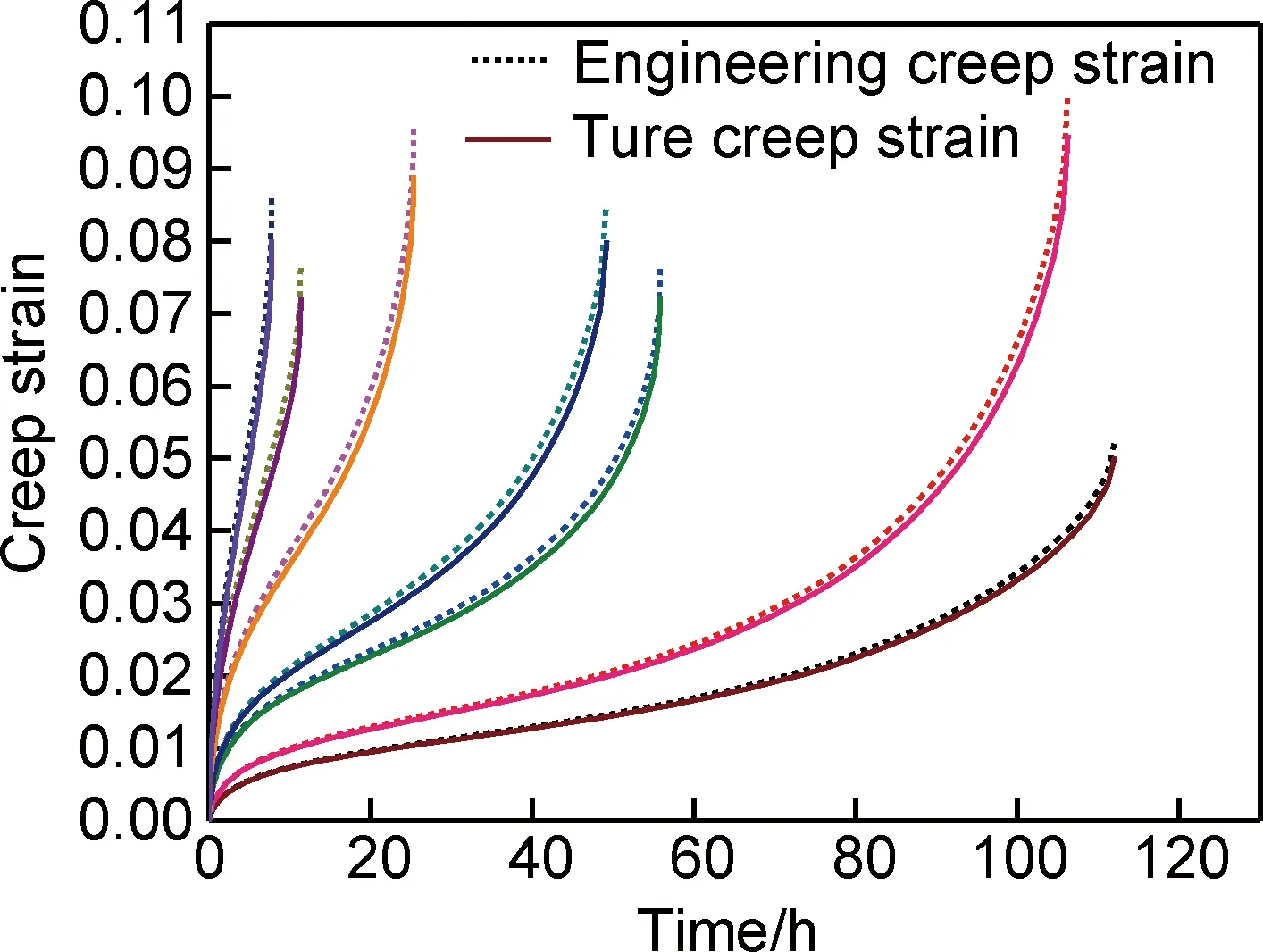
图5　TC11钛合金500 ℃下的蠕变曲线Fig.5　Creep curves of TC11 tilanium alloy at 500 ℃

在500 ℃下TC11钛合金缺口持久寿命试验结果见表1。

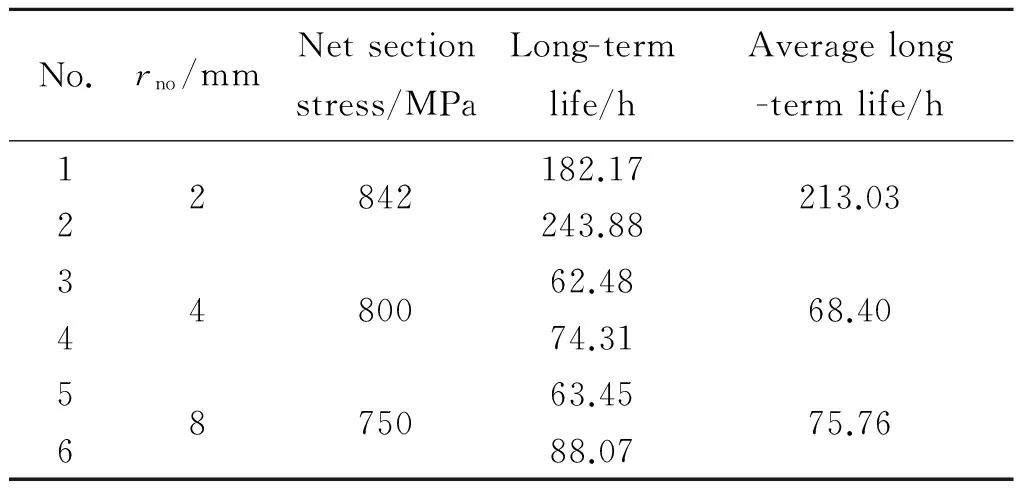
表1　TC11缺口500 ℃下的持久寿命试验结果

3　TC11缺口持久寿命预测与结果分析

3.1TC11钛合金的弹塑性蠕变本构模型

为采用大变形有限元分析方法预测TC11缺口的持久寿命，并和基于小变形分析的预测方法进行对比分析，根据TC11的拉伸应力-应变曲线和蠕变曲线，分别建立了基于真应力-真应变的弹塑性蠕变本构模型和基于工程应力-应变的弹塑性蠕变本构模型，本构模型材料参数拟合结果分别见表2和表3。

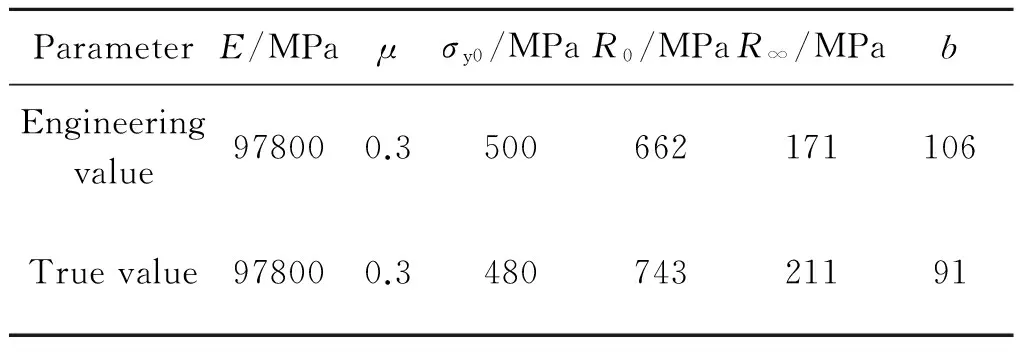
表2　TC11钛合金500 ℃下弹塑性本构模型材料参数

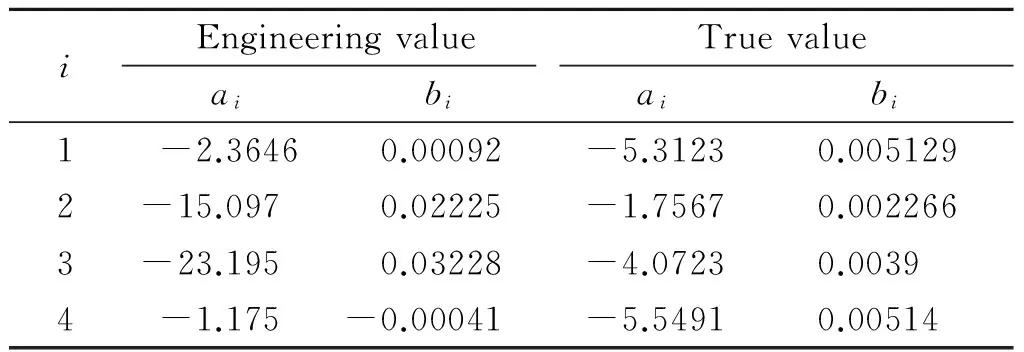
表3　TC11钛合金500 ℃下的蠕变本构模型材料参数

3.2基于大变形有限元分析的TC11缺口持久寿命预测

采用ANSYS有限元软件对TC11缺口的弹塑性和蠕变响应进行计算分析。对于蠕变本构模型，采用用户材料子程序进行编译和调用。根据缺口的几何和载荷对称性建立TC11缺口的轴对称有限元模型，如图6所示。模型底端施加Y向约束，顶端施加缺口持久寿命试验的载荷。

图6　缺口圆棒轴对称有限元模型Fig.6　Axisymmetric finite element model of notched bars (a)rno=2 mm;(b)rno=4 mm;(c)rno=8 mm

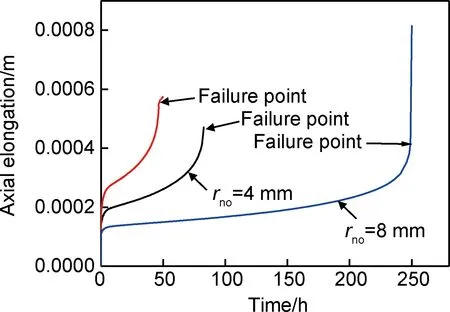
图7　模型轴向伸长量随时间变化曲线Fig.7　Model’s axial elongation curves changeing with time

三种TC11缺口的弹塑性蠕变响应的大变形有限元分析结果如图7所示。可以看出，采用大变形有限元分析可以预测出TC11缺口的整体轴向变形响应，变形呈现与蠕变曲线类似的三个阶段特征。根据变形响应曲线停止计算的时间，可获得基于大变形分析的TC11缺口持久断裂寿命，并与试验结果进行对比分析，结果见表4。由表4中结果可知，本工作提出的基于大变形有限元分析的持久寿命预测方法可以较准确地预测TC11缺口的持久寿命，预测结果分布在试验结果的±40%误差带内。

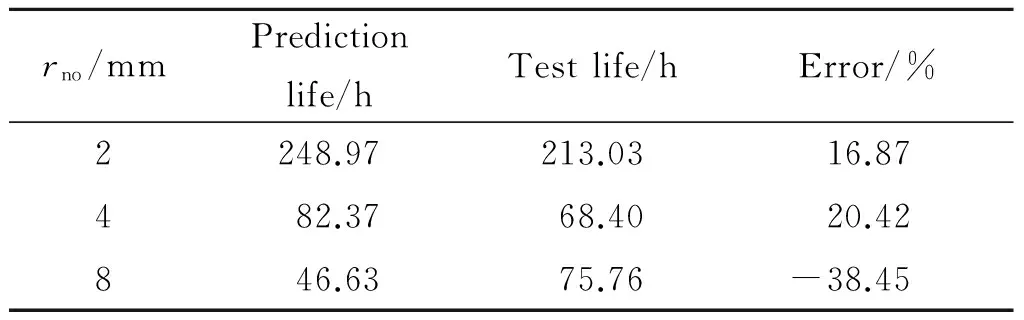
表4　基于大变形分析的寿命预测结果

3.3基于小变形有限元分析寿命预测

为更好地评价本工作提出的持久寿命预测方法，采用几种基于小变形分析结果的预测方法对TC11缺口的持久断裂寿命进行预测，并和本工作提出的预测方法的结果进行对比分析。

3.3.1TC11钛合金持久热强参数方程

基于小变形分析的预测方法一般根据构件的小变形应力-应变分析结果结合材料的持久寿命方程进行寿命预测。根据TC11光滑试样的蠕变和持久试验结果，可拟合获得其Larson-Miller持久热强参数综合方程为：

lgσ=2.8376-1.59P-16.202P2-2205.227P3

(3)

热强参数P为：

P=T(lgt-1.1)/105

(4)

式中：T为兰氏度，°R。

3.3.2基于小变形有限元分析寿命预测

(1)基于关键点断裂应变的寿命预测

关键点断裂应变理论认为，当结构内部任意位置蠕变应变累积超过某一临界值时，结构发生持久断裂失效。以缺口半径为2 mm的试样小变形有限元分析结果为例，可获得缺口试件最小截面上不同点的蠕变应变随时间的变化关系，如图8所示。图中a～f点为缺口试样最小截面上的不同位置的点。根据TC11光滑试样的蠕变断裂应变，可获得缺口试件的持久寿命。考虑到TC11蠕变断裂应变的分散性，这里选取两种不同的蠕变断裂应变来预测其持久寿命，预测结果与实验结果的对比见表5。

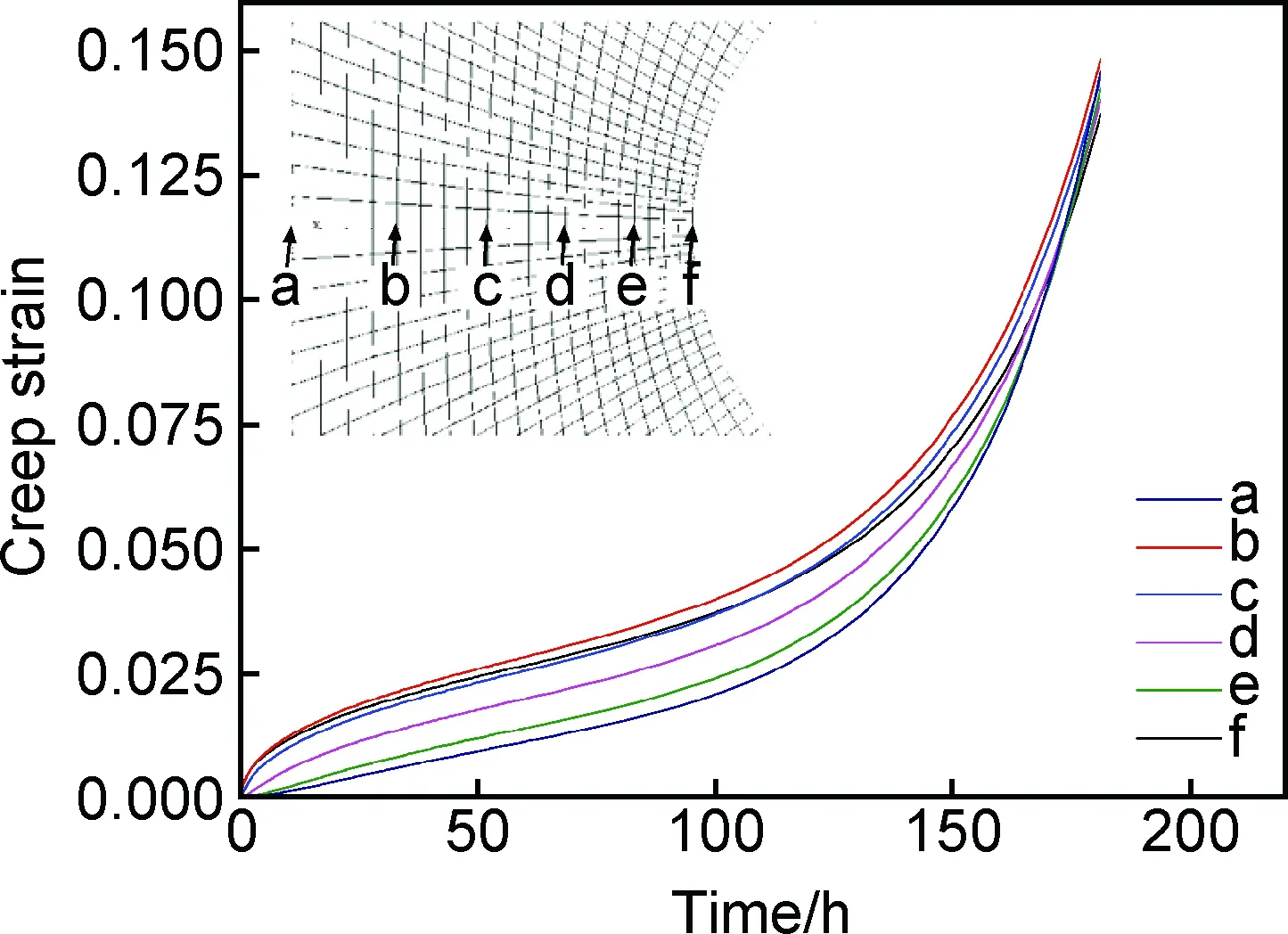
图8　最小截面关键点蠕变应变Fig.8　Creep strain of the key nodes on the minimum section

rno/mmCreeprapturestrainPredictedlife/hTestlife/hError/%20.05121.30.10163.9213.03-43.10-23.1040.0557.50.1087.768.40-15.9028.2280.0527.80.1054.675.76-63.30-27.90

(2)基于平均有效应力的寿命预测

基于平均有效应力的寿命预测方法是将缺口试件最小截面上的有效应力作为持久热强参数综合方程(3)中的参考应力，根据持久热强参数综合方程(3)来预测缺口试件的持久寿命，预测结果见表6。

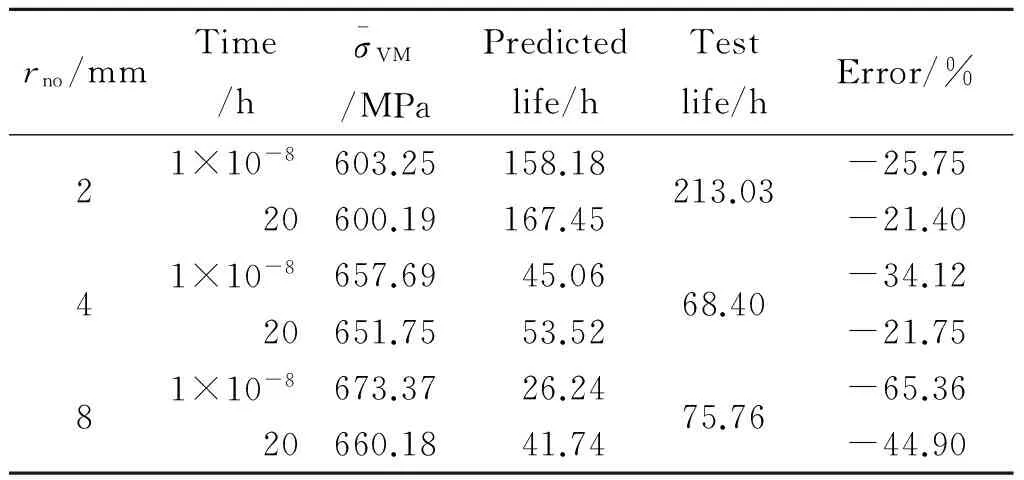
表6　基于最小截面平均有效应力的寿命预测结果

(3)基于骨点应力的寿命预测

对于高温拉伸作用下的轴对称构件(例如缺口圆棒)，其在最小截面上总存在一点，该点的应力状态不随时间变化而变化，也与材料的弹塑性及蠕变性能无关，这一点就是骨点(skeletal point)，与之对应的应力称为骨点应力[17]。将骨点应力与持久热强参数方程(3)结合可预测试样的持久寿命。

以缺口半径为2 mm的试样为例，其最小截面上的Von Mises应力分布如图9所示，由此可确定其骨点应力。根据骨点应力预测的三种缺口试件的持久寿命见表7。

图9　不同时刻最小截面应力沿径向分布Fig.9　　　　Stress distribution along radial direction of the minimum section at different time

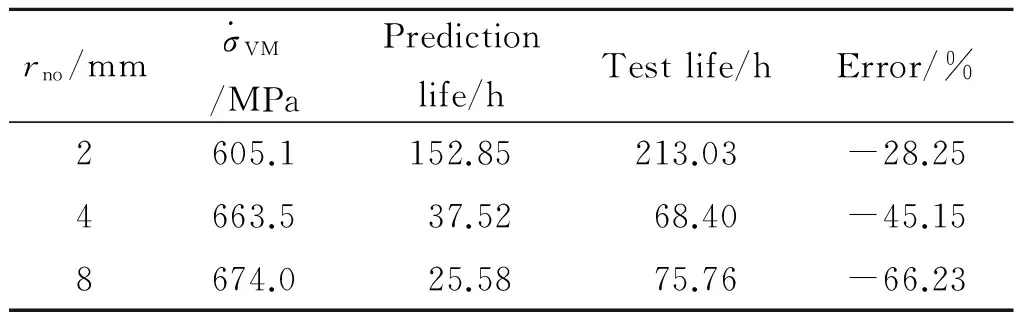
rno/mmσVM/MPaPredictionlife/hTestlife/hError/%2605.1152.85213.03-28.254663.537.5268.40-45.158674.025.5875.76-66.23

3.4讨论

基于大变形有限元分析的持久寿命预测方法由于考虑了实际构件在失效时已累积的较大变形，使得预测结果与试验结果的误差在±40%以内，并可推广应用于复杂变温结构。而基于小变形有限元分析的寿命预测方法由于未充分考虑缺口件的实际大变形响应导致其预测误差均超过±60%，其中基于关键点断裂应变方法预测结果与蠕变断裂应变的选取有关，而一般蠕变断裂应变与温度、应力状态等有关，实际应用中不好确定。

4　结论

(1)基于大变形有限元分析的持久寿命预测方法能较好地预测500 ℃下三种TC11缺口圆棒试样的持久寿命。

(2)三种基于小变形有限元分析的持久寿命预测方法预测精度较本工作提出的方法低。

(3)基于关键点断裂应变以及基于平面有效应力的寿命预测方法由于试样内部应力应变随时间变化，因此难以准确选定断裂应变和参考应力。

[1] HYDE T H, XIA L，BECKER A A. Prediction of creep failure in aeroengine materials under multi-axial stress states[J]. Int Mech Sci,1996,38 (4): 385-403.

[2] 赵彩丽,刘新宝,郝巧娥,等.高温金属构件蠕变寿命预测的研究进展[J].材料导报，2014, 28 (12):55-59.

(ZHAO C L, LIU X B, HAO Q E,etal. The research progress of high temperature metal components creep life prediction [J].Materials Review, 2014, 28 (12):55-59.)

[3] 曾立英,戚运莲,洪权,等. 固溶时效处理Ti-600合金的蠕变行为研究[J].稀有金属材料与工程，2014, 43 (11):2697-2701.

(ZENG L Y, QI Y L, HONG Q,etal. The creep behavior research of solid solution aging treatment of Ti-600 alloy [J].Rare Materials and Engineering，2014, 43 (11):2697-2701.)

[4] 董露,郭子静,王丹妮,等.Ti40钛合金持久寿命及其预测方法[J].理化检验：A(物理分册)，2014, 50(9):636-680.

(DONG L, GUO Z J, WANG D N,etal. The durable life and its prediction method of Ti40 titanium alloy [J]. Physical Testing and Chemical Analysis： A (Physical Testing)，2014, 50 (9):636-680.)

[5] 李学雄,夏长清,戚延龄,等. TC6钛合金的高温拉伸蠕变行为研究[J]. 稀有金属材料与工程， 2013, 42(9):1901-1904.

(LI X X, XIA C Q, QI Y L,etal. The high temperature tensile creep behavior research of TC6 titanium alloy [J]. Rare Materials and Engineering, 2013, 42 (9):1901-1904.)

[6] OH C S, KIM N H N, KIM Y J,etal. Creep failure simulations of 316H at 550 ℃: part I—a method and validation [J]. Eng Fract Mech, 2011, 78(17):2966-2977.

[7] 孙永娜,吴向东,万敏. 基于时效校形的TB5合金蠕变本构模型建立[J].塑性工程学报， 2013, 20 (1):76-79.

(SUN Y G, WU X D, WAN M. Creep constitutive modeling of TB5 alloy based on the aging rectification [J]. Journal of Plasticity Engineering, 2013, 20 (1):76-79.)

[8] LIU D S, ZHANG D X, LIANG J W,etal. Predictions of creep rupture life of a V-notched bar in DD6 Ni-based single crystal superalloy [J]. Mater Sci Eng A, 2014, 615:14-21.

[9] HUANG J, SHI D Q, YANG X G,etal. Effect of multi-axial stress state on creep behavior and stress rupture life of a Ni-based DS superalloy[J].Comp Mater Sci, 2014, 85:20-31.

[10]GOYAL S, LAHA K, DAS C R,etal.Finite element analysis of uniaxial and multiaxial state of stress on creep rupture behaviour of 2.25Cr-1Mo steel[J].Mater Sci Eng A,2013,563:68-77.

[11]GOYAL S, LAHA K. Creep life prediction of 9Cr-1Mo steel under multiaxial state of stress [J]. Mater Sci Eng A, 2014, 615:348-360.

[12]EVANS R W, PARKER J D, WILSHIRE B. Recent advance in creep and fracture of engineering materials and structures [M]. Swansea, UK: Pine ridge Press, 1982.

[13]曹春晓. 钛在航空领域的重要地位和关键作用[J]. 中国金属通报, 2013(4):16-19.

(CAO C X. Important position and key role of titanium in the field of aviation [J]. China Metal Bulletin， 2013(4):16-19.)

[14]常辉,周廉,王向东. 我国钛工业与技术进展及展望[J]. 航空材料学报， 2014, 34(4):37-43.

(CHANG H, ZHOU L, WANG X D. Progress and prospect of titanium industry and technology in China [J]. Journal of Aeronautical Materials, 2014, 34(4):37-43.)

[15]陈慧琴,林海,郭灵,等. TC11钛合金热变形特性分析及其本构关系的建立[J]. 材料工程， 2007 (8):32-36.

(CHEN H Q, LIN H, GUO L,etal. Hot deformation characteristics and constitutive relation of TC11 alloy [J]. Journal of Materials Engineering, 2007 (8):32-36.)

[16]陈慧琴,林好转,郭灵,等. TC11钛合金高温流变行为及组织演变[J]. 航空材料学报， 2007, 27(3):1-5.

(CHEN H Q, LIN H Z, GUO L,etal. Rheological behavior and microstructure evolution of TC11 titanium alloy at elevated temperature [J]. Journal of Materials Engineering, 2007, 27(3):1-5.)

[17]HAYHURST D R, HENDERSON J T. Creep stress redistribution in notched bars [J]. Int J Mech Sci, 1977, 19:133-146.

Creep Rupture Life Prediction Based on Analysis of Large Creep Deformation

YE Wenming1，HU Xuteng1，MA Xiaojian2，SONG Yingdong1,3

(1. Jiangsu Province Key Laboratory of Aerospace Power System, College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China； 2. Compressor Laboratory, AVIC Shenyang Engine Design Institute, Shenyang 110015,China； 3. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)

A creep rupture life prediction method for high temperature component was proposed. The method was based on a true stress-strain elastoplastic creep constitutive model and the large deformation finite element analysis method. This method firstly used the high-temperature tensile stress-strain curve expressed by true stress and strain and the creep curve to build materials’ elastoplastic and creep constitutive model respectively, then used the large deformation finite element method to calculate the deformation response of high temperature component under a given load curve, finally the creep rupture life was determined according to the change trend of the responsive curve.The method was verified by durable test of TC11 titanium alloy notched specimens under 500 ℃, and was compared with the three creep rupture life prediction methods based on the small deformation analysis. Results show that the proposed method can accurately predict the high temperature creep response and long-term life of TC11 notched specimens, and the accuracy is better than that of the methods based on the average effective stress of notch ligament, the bone point stress and the fracture strain of the key point, which are all based on small deformation finite element analysis.

creep rupture life prediction; creep constitutive; TC11 titanium; notch samples; finite element analysis

(责任编辑：徐永祥)

2015-10-08；

2015-12-01

胡绪腾(1980—)，男，博士，讲师，主要研究方向发动机结构完整性与耐久性，(E-mail)xthu@nuaa.edu.cn。

10.11868/j.issn.1005-5053.2016.4.011

TG146.23

A

1005-5053(2016)04-0078-06