几何功能约束最小二乘法双短圆弧检测

彭希锋 陈爽 李海星 熊朝晖

摘 要：针对双短圆弧的准确检测难题，首先从工件的几何功能使用要求出发，详细分析使用三坐标测量机检测双短圆弧时误差产生的原因与影响；然后根据误差产生的原因，提出基于几何功能约束最小二乘拟合的双短圆弧检测方法。该方法将双短圆弧的设计半径、相对位置关系以及圆弧整体轮廓与工作基准的位置作为最小二乘圆拟合的约束条件，以降低拟合的误差。将该检测方法与经典最小二乘圆弧分段拟合检测方法进行对比实验，结果表明：提出的方法能够很好地改善最小二乘法对双短圆弧的拟合质量，有效降低检测结果的“误判”风险，可为双短圆弧的精确检测提供一种可靠方法。

关键词：最小二乘法；几何功能约束；双短圆弧检测；三坐标测量机

文献标志码：A 文章编号：1674-5124（2016）09-0036-05

0 引 言

计量界将30°以下中心角所对的圆弧归为短圆弧，在机械加工精密检测领域，短圆弧的准确测量一直是难题。由于短圆弧上的特征点数少，且过于集中，在进行圆弧的拟合时其形状误差与测量误差被过度放大，往往得不到理想的检测结果[1]。在短圆弧检测误差的控制方法上，邵伟国[2]、朱嘉[3]、李在峥[4]等提出了基于圆心约束的最小二乘圆拟合方法。该类方法通过固定圆心值的方式，有效提高拟合精度。张振友[5]与刘珂等[6]提出了半径约束最小二乘圆拟合方法，可以有效提高圆中心定位精度，进而改善拟合质量。刘元朋等[7]通过引入系数约束条件式，对拟合方程的系数进行相关约束，结果表明能提高拟合精度。袁道成等[8]提出通过分段密集采点，对测量的粗大误差和随机误差进行衰减后再拟合的方法，能有效改善短圆弧的检测质量。

然而，上述方法都是针对单一短圆弧的检测误差控制，对于双短圆弧检测的应用仍有局限性。本文从产品的几何功能分析出发，通过对三坐标测量机检测双短圆弧时的误差与影响进行分析，将双短圆弧的设计半径、相对位置关系以及圆弧整体轮廓与工作基准的位置作為最小二乘拟合的约束条件，以降低拟合的误差与影响，为双短圆弧的精确检测提供一种可靠方法。

1 双短圆弧的检测要求与测量方法

1.1 检测要求

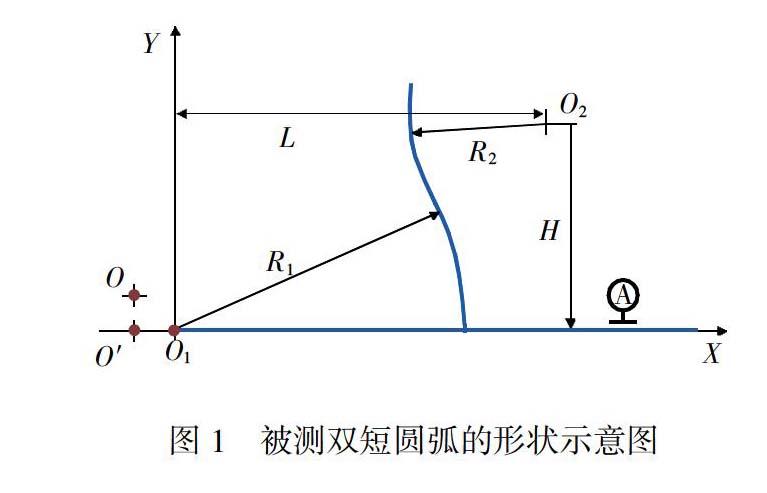
被测圆弧的设计形状如图1所示，共有两段相切圆弧。圆弧1的圆心在基准A上，圆弧2的圆心与圆弧1在水平和纵向的距离分别为L与H，要求对两段圆弧的半径进行检测，半径值分别为R1±Δ1，R2±Δ2。其中，Δ1、Δ2分别为设计图纸上R1、R2的允许误差限。

1.2 测量方法

圆弧的检测在Leitz PMMC-700P三坐标测量机（Hexagon，瑞典）上进行，其空间长度测量误差为（0.6+L/600）μm。测量时，首先测量并建立基准A。为了使测量圆弧时得到较优的半径补偿矢量，先手动在圆弧1上采点并拟合出最小二乘圆心O，然后将O平移至基准A上建立测量坐标系基准点O′。以O′为圆心，在自动测量模式下测量圆弧1，并在基准A上建立新的测量基准点O1，再以O1为圆心，在自动模式下测量圆弧1作为最终结果。上述反复迭代精建测量基准点的目的是尽可能降低触测力不稳定与半径补偿矢量方向不准确带来的测量误差，从而提高测量点的质量。测量圆弧2时，将测量基准点O1按相应的方向在水平上平移L，纵向平移H得到测量基准点O2，以O2为圆心在自动模式下测量圆弧2作为最终结果。

2 数据计算方法及问题的提出

工件的检测对象为两段圆弧的半径，可通过对测量点云进行圆弧拟合后评价。圆弧的拟合方法主要有最小包容区域法、最小外接圆法、最大内切圆法、最小二乘法等。前3种方法由于在数学上不能获得直接的解析解，所以只能通过基于小偏差假设和小误差假设的近似算法进行求解，其求解过程需要较为复杂费时的迭代，操作不便，且通常只能局限于一定的应用范围。最小二乘法具有运行速度快和性能稳定等特点，且容易获得解析解，因此获得广泛的应用。

所采用的Leitz PMMC-700P坐标测量机内置有QUINDOS 6.0操作软件，软件自含最小二乘拟合的程序。因此，通常的做法是使用自带的程序分别对圆弧1和圆弧2的测量点进行最小二乘拟合，计算获得相应的半径R1和R2。但是，上述计算操作会带来以下问题：

1）短圆弧自身形状误差和测量机误差对半径拟合精度的影响会增大检测结果发生“误判”的风险。

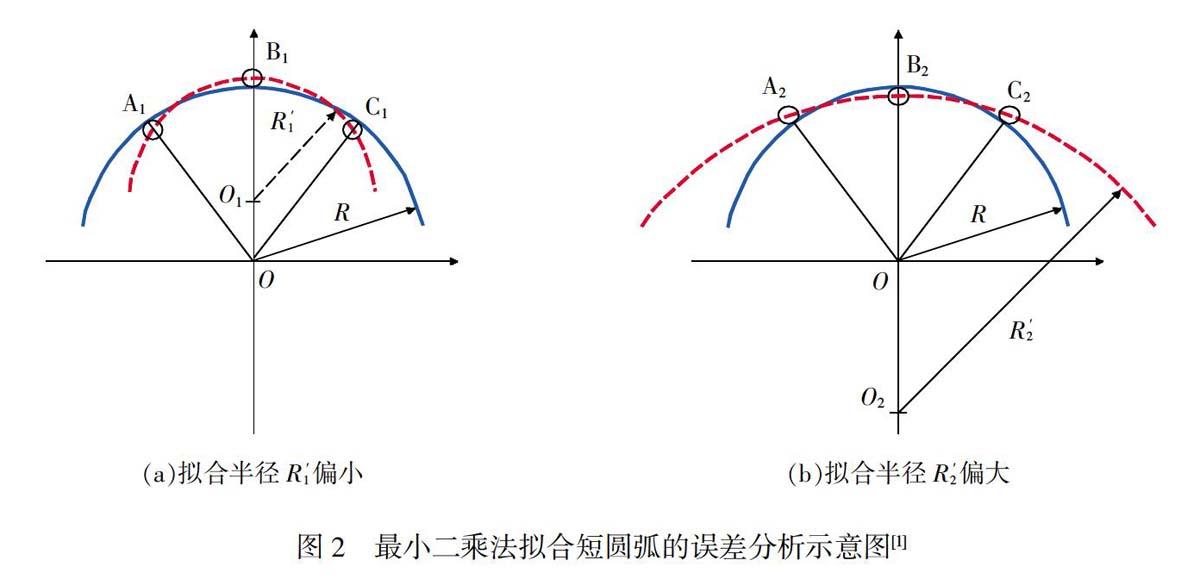
如图2所示，以三点定圆为例，由于短圆弧形状误差与测量机测量误差的存在，测量点集（A1，B1，C1）与（A2，B2，C2）偏离理想轮廓（实线部分），造成拟合圆弧（虚线部分）的不准确，导致拟合半径过度的缩小与放大。

假设短圆弧的形状误差与测量机的测量误差之和为e，被测短圆弧包含的圆心角大小为α。根据蒲竞秋等[1]的推导结果，三点定圆时短圆弧半径最小二乘法拟合误差的放大系数为

N=ΔR/e=■-1（1）

式中：ΔR——半径拟合误差；

e——短圆弧的形状误差与测量机的测量误差之和；

α——被测短圆弧的圆心角。

如图3所示，由式（1）可知用最小二乘法进行短圆弧的拟合时，其半径拟合误差随圆心角的减小而增大，随e值的增大而增大。当圆心角处于10°以下的范围内时，半径拟合误差的放大效应最剧烈。当圆心角α=10°时，e在1，3，5，10 μm下的半径拟合误差分别为524.6，1 573.7，2 622.9，5 245.8 μm。即使在圆心角α=30°，e=5 μm时，其半径拟合误差仍高达288.5 μm。

从上述分析可知，使用坐标测量机进行短圆弧的检测时，若直接使用最小二乘法进行圆弧的拟合，误差被过度放大，很难获得准确的检测结果。本文的工件属于短圆弧测量，其每段圆弧的坐标点采集圆心角为25°，若直接采用软件自带的最小二乘算法分别进行各段圆弧的拟合，会产生较大的拟合误差，增加检测结果“误判”的风险。

2）分段拟合破坏了两段圆弧的相对位置关系，检测结果不符合产品几何功能使用要求。

本文的工件是一种仿形样板检具，使用过程中，要求两段圆弧同时起检测作用，即要求保证两段圆弧的相对位置关系固定。最小二乘法拟合圆弧时同时有圆心与半径两个求解目标，其拟合的误差也会相应地反映到两个求解目标上。从图2可以看出，短圆弧拟合时，不仅有半径的放大效应，同时也有圆心位置的放大效应，破坏了两段圆弧的相对位置关系，导致检测结果不符合产品的整体几何功能使用要求，也有可能加大“误判”的风险。

如图4所示，不考虑拟合误差、测量误差等因素，由于实际加工误差的存在，圆弧1和圆弧2的实测点集Pi1与Pi2偏离了设计轮廓（实线部分），偏离的距离为δ，且δ>（Δ1+Δ2）（Δ1、Δ2分别为R1、R2的允许误差限）。但是，由于圆弧的形状加工精度较好，使得实测点拟合后的圆弧半径R1′≈R1，R2′≈R2，此时就导致了错误的检测结果。其错误有两个方面：1）拟合圆心O1′偏离工作基准面A，不符合工件的使用功能；2）虽然拟合圆弧半径合格，但是两个圆弧之间偏距δ超过了圆弧轮廓的允许误差。

4 实验对比分析

为了对前面的分析结果进行检验，抽取一个工件的坐標测量数据，分别使用经典的最小二乘法与基于几何功能约束的最小二乘法进行拟合，然后计算两段圆弧圆心相对位置的变化及各测量点到拟合圆弧圆心半径与设计轮廓半径的误差，分别进行对比分析。

将双短圆弧工件的测量点数据导出并上传到Matlab程序（编制程序已使用均布的标准圆进行拟合验证，其圆心与半径的数据拟合误差均小于10-11），计算得到结果如表1和图5所示。

表1是两种拟合方法的圆心位置变化量，从结果可以看出，使用经典最小二乘法对两段圆弧进行分段拟合时，其圆心都有往右上方的偏移量，且其值受短圆弧拟合放大效应的影响，偏移量较明显，使拟合轮廓脱离了工作基准面A，不符合实际使用要求。另外从两个圆心变化量可以看出，两段圆弧的相对位置也发生了变化，水平与纵向变化分别为ΔL=Δx2-Δx1=0.947 8 mm，ΔH=Δy2-Δy1=-0.056 7 mm，变化量也较明显，破坏了两段圆弧轮廓的整体性，检测结果不符合产品的几何功能。使用本文带约束的方法进行拟合时，其本身并未破坏产品的几何功能，两段圆弧的整体性得到保持，且圆弧轮廓一直约束在工作基准A上，只是将圆弧轮廓沿着基准A平移使各测量点到设计轮廓的距离偏差平方和最小，计算的偏移量结果d=0.343 1 mm。该段偏移量可能由两方面原因造成，一是加工误差引起；二是测量坐标系构建误差引起。

图5是两种方法拟合的短圆弧半径与设计轮廓半径的偏差。从结果可以看出，使用经典最小二乘法对两个圆弧分段拟合时，其半径误差由于短圆弧的放大效应已经远大于工件的允许误差限（±0.02 mm）。其中，圆弧1的最大半径偏差为0.184 7 mm，圆弧2的最大半径偏差为0.106 6 mm。另外，从结果可以看出两段圆弧对设计轮廓半径的偏离呈相反方向（图5（a）），轮廓的整体性在表1圆心偏离的基础上进一步被破坏，较大程度地背离了产品的几何功能要求。使用本文带几何功能约束的最小二乘法进行拟合时，不会破坏两段圆弧轮廓的整体性也不会破坏两段圆弧的相对位置关系。从结果来看，各测量点对设计轮廓的偏离量较小，其中圆弧1的最大半径误差为0.013 7 mm，圆弧2的最大半径误差范围为0.017 9 mm。

本文的拟合算法是在经典的最小二乘法上直接施加产品几何功能的约束。根据Gander W[10]与Lukacs G等[11]的研究，在拟合圆时，最小二乘法虽然能够获得解析解，但其解也有自身的不确定度。优化后的变型最小二乘算法精度比经典的最小二乘算法精度高，但是其计算较为复杂。由于本文工件的检测误差限要求相对不高，因此选用经典最小二乘法施加约束后直接求解，能够满足要求和提高编程效率。后续有较高精度的检测要求时，可以考虑在本文方法的基础上采用优化的最小二乘算法进行圆弧的拟合。

本文研究的问题主要是工件测量数据的计算问题，因此对双短圆弧工件的测量控制方法涉及不多。根据袁道成等[8]的研究，对单一短圆弧进行检测时，通过分段密集采样法可以有效地对测量的随机误差进行衰减，从而提高检测精度。理论上，该种检测方法也可用于双短圆弧的检测，在高精度的检测场合可以结合测量与数据处理两方面优化进行，其作用仍需进一步分析。

本文研究的案例为二维双短圆弧段线的检测，理论上本文的方法也可以为三维双短圆弧面的检测提供借鉴，但其效用程度仍需进一步分析。

5 结束语

针对双短圆弧的精密检测难题，详细分析了双短圆弧检测误差产生的原因，提出了基于几何功能约束最小二乘拟合的双短圆弧检测方法。实验验证表明，该检测方法能够很好地改善经典最小二乘法对双圆弧分段拟合的误差，检测结果不破坏双圆弧轮廓的整体性及其与工作基准的位置关系，检测结果符合产品的几何功能使用要求，能够有效提高检测结果的准确性，降低“误判”风险，为双短圆弧的精确检测提供了一种可靠方法。

参考文献

[1] 蒲竞秋. 短圆弧测试方法与误差分析[J]. 机械，2002，29（S1）：35-36.

[2] 邵伟国，王霄. 非接触式三坐标测量短圆弧方法研究[J]. 测控技术，2013，32（6）：140-141.

[3] 朱嘉，李醒飞，谭文斌，等. 基于圆心约束最小二乘圆拟合的短圆弧测量[J]. 光学精密工程，2009，17（10）：2486-2492.

[4] 李在峥. 基于圆心定位的短圆弧小曲率样板精密测量新方法[J]. 计测技术，2013，33（4）：69-70.

[5] 张振友，李明. 精密坐标测量中小段圆弧的一种评价方法[J]. 机械制造，2008，46（2）：63-66.

[6] 刘珂，朱富强，张广军. 半径约束最小二乘圆拟合方法及误差分析[J]. 光电子·激光，2006，17（5）：604-607.

[7] 刘元朋，张定华，桂元坤，等. 用带约束的最小二乘法拟合平面圆曲线[J]. 计算机辅助设计与图形学报，2004，

16（10）：1382-1385.

[8] 袁道成，伏德贵. 圆弧测量误差分析及其应用[J]. 计量技术，1999（7）：15-17.

[9] 徐国旺，廖明潮. 拟合圆的集中方法[J]. 武汉工业学院学报，2002（4）：104-106.

[10] GANDER W， GOLUB G H. Least -square fitting of circles and ellipses[J]. BIT，1994，34（4）：558-578.

[11] LUKACS G， MARTIN R R. Faithful least-squares fitting of spheres， cylinders cones and tori for reliable se-gmentation[C]∥Proceedings of the 5th European Conference on Computer Vision Freiburg Germany，1998：671-686.

（编辑：刘杨）