基于最小二乘法的电力系统谐波与间谐波检测方法
刘小林 扈罗全


摘 要:為能够对电力系统中谐波与间谐波信号进行精确的检测,提出一种基于最小二乘法的谐波与间谐波检测方法。首先从数学理论和工程应用论证该方法在谐波与间谐波检测中的可行性。该方法用最小二乘法对被测信号进行函数拟合,通过拟合函数的系数实现谐波与间谐波的检测。通过对实际应用中典型信号的Matlab仿真表明,该方法能够准确检测谐波与间谐波分量的频率、幅值和相位角,且计算量较小。通过对标准IEC 61000-4-7中两种典型情况的分析表明,该方法能够为需要精确测量谐波与间谐波分量的场合以及未来IEC 61000-4-7的修订提供一种可选择的方法。
关键词:电力系统;谐波检测;间谐波检测;最小二乘法;条件数;曲线拟合
文献标志码:A 文章编号:1674-5124(2016)09-0031-05
0 引 言
近年来,随着各种非线性电力电子设备在电力系统中的广泛使用(如各种整流设备、交直流换流设备、电弧炉、可控硅整流设备、电子调速设备等),使大量的谐波间谐波电流注入电网,造成电网电压畸变,供电质量下降,严重危害供电设备、用电设备以及人的生命财产安全[1-2]。为使电网能够安全运行,将谐波间谐波控制在安全的范围内,必须对电网中的谐波间谐波进行治理。
治理谐波间谐波的关键是对其进行准确有效的分析。从国内外的现状来看,目前主要的谐波间谐波的分析方法有:基于快速傅里叶变换(FFT)的方法[3-4]、基于小波的分析方法[5-6]、基于瞬时无功功率理论的检测方法[7]与基于人工神经网络的分析检测方法[8]等。算法是一种全局的变换方法,能精确地检测整数次谐波,但不能检测非整数次谐波,而且伴有频谱泄漏和栅栏现象,虽然出现了许多改进算法如插值、加窗等,但仍有许多不足;小波分析方法是时间窗和频率窗都可改变的时频局部化分析方法,其对信号分析具有自适应性,不仅适合于稳态信号,也适合于时变信号的分析。但目前几乎所有的小波函数在信号分析中都存在小波混叠和能量泄漏现象,使得其在谐波间谐波检测中存在精度低、鲁棒性差、分辨率低等问题;基于瞬时无功功率的检测方法无法实现对间谐波的检测且计算量大;基于人工神经网络的检测方法存在计算量大、实时性不强的缺点且应用于谐波间谐波问题的处理尚处在起步阶段。结合上述讨论与目前的研究现状,提出基于最小二乘法的谐波与间谐波的检测。
本文首先介绍最小二乘法原理;然后提出基于最小二乘法的谐波间谐波检测算法,并通过结合数学理论与工程应用论证了该方法的可行性;最后通过对典型信号进行仿真,验证该方法的有效性。
3 检测算法的数学基础
基于最小二乘法的曲线拟合进行谐波间谐波成分分析时,其系数矩阵G是必须考虑的重要因素。用最小二乘法拟合曲线时,系数矩阵通常是病态的。病态系数矩阵若有微小扰动,其解向量将产生巨大变化。病态系数矩阵对拟合曲线产生很大的误差,使得基于最小二乘法的曲线拟合分析问题常不能得到正确的结果。在谐波间谐波的分析中,电磁环境中的扰动是不可避免的。在使用最小二乘法进行谐波间谐波分析时应确保其系数矩阵是非病态矩阵(即良态矩阵)。因此在用最小二乘拟合曲线对谐波间谐波分析时,对系数矩阵进行数学分析是必要的。
在选择非病态矩阵时,相关资料中用条件数去刻画。当A的条件数cond(A)ν相对地大时,矩阵是病态的;当A的条件数cond(A)ν相对地小时,矩阵是良态的。且对于任何非奇异矩阵A都有cond(A)ν≥1[9]。
由以上被测信号模型以及函数族{1,cosx,sinx,…,cosnx,sinnx}在区间[0,2π]上正交。由文献[9]可知,在满足采样定理的条件下选择数据区间的长度为2π的整数倍时,在一定精度下,经计算可得其系数矩阵是对角阵,且其条件数cond(G)ν为1,可判断其系数矩阵为良态矩阵。因此用最小二乘曲线拟合可对谐波间谐波进行有效分析。同时,在满足采样定理的条件下选择数据区间的长度为2π的整数倍时,所得到的对角阵形式的系数矩阵,满足工程应用。在工程应用中,逆矩阵的求解是一个很复杂的过程。特别是当矩阵的阶数比较大时,在许多实时处理的场合,逆矩阵的求解已成为工程应用中急需解决的棘手难题。对角形式的系数矩阵的求逆是一个很简单的过程,只需将对角线上的元素求逆即可,这大大简化了逆矩阵的求解过程。通过理论和工程应用分析,最小二乘法曲线拟合可应用于电力系统谐波间谐波成分分析。
提高最小二乘法拟合函数中的频率分辨率可以满足一定精度电力系统谐波间谐波成分的测量。
4 检测方法的仿真与分析
本文仿真基于Matlab平台。通常在谐波发射测量过程中,3次谐波值对于评估谐波电流发射特性具有很好的代表性[12]。基于此,在验证方法有效性的基础上,本文选用含有3次、5次谐波及间谐波的典型信号进行仿真,即选用谐波间谐波频率检测范围为1~300 Hz,在实际应用中可根据需要提高采样频率与扩大频率检测范围来扩大谐波间谐波分量频率测量范围。为说明方法在实际应用中的价值,在对大量信号进行测试的基础上,选用信号部分来源于IEC 61000-4-7[4](在不影响验证方法有效性的基础上,对选用信号的频率、幅值或相角进行了修改),部分来源于相关文献。
4.1 标准IEC 61000-4-7中不含突变典型信号谐波间谐波的检测
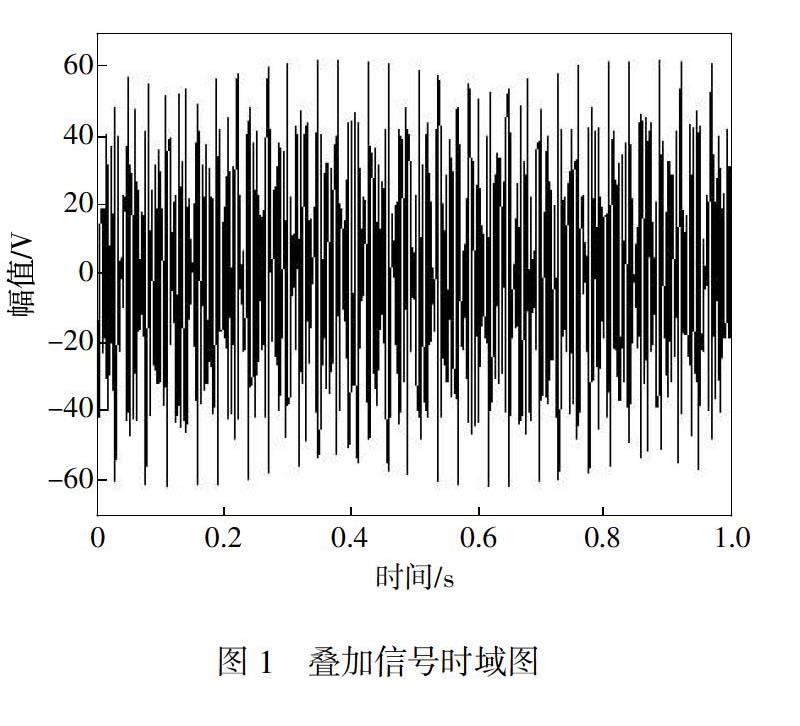
仿真信号实例y(t)来源于国际标准IEC 61000-4-7[4],该信号为一个均方根值保持为23 V、频率f3为178 Hz的通信信号叠加在系统中已存在频率f1、 f2分别为150,250 Hz的3次和5次谐波(幅值均为11.5 V)之上的叠加信号,它们的初相角均为0°,如图1所示。其表达式为
y(t)=11.5×■(sin(2πf1t)+sin(2πf2t))+
23■sin(2πf3t)(11)
其中,150 Hz与250 Hz分别为3次、5次高倍谐波分量;187 Hz为非线性元件产生的非整数次谐波分量即间谐波分量。
设置采样频率为1 000 Hz,采样点数为1 000,时间窗口的宽度为1 s。检测谐波间谐波分量的频率范围设置为1~300 Hz,频率分辨率为1 Hz(即式(7)中的ω=2π)。满足采样定理以及数据区间的长度为2π的整数倍。应用最小二乘法拟合曲线对信号进行分析,得到其幅值相位表见表1。
由表可以看出在不含突变信号谐波间谐波的检测中,该方法可以精确地检测出谐波间谐波的频率、幅值、相位角。
4.2 标准IEC 61000-4-7中含突变典型信号谐波间谐波的检测
仿真信号来源于国际标准IEC 61000-4-7[4],为说明方法的有效性,对其进行了适当的修改。该信号为初相角为90°,有效值为3.54 V,频率为150 Hz的3次谐波信号与在20个基波周期后出现的脉冲宽度为0.01 s的单位矩形脉冲信号的叠加信号。其时域波形如图2所示。
设置采样频率为1 000 Hz,采样点数为1 000,时间窗口的宽度为1 s。检测谐波间谐波分量的频率范围设置为1~200 Hz,频率分辨率为1 Hz(即式(7)中的ω=2π)。满足采样定理以及数据区间的长度为2π的整数倍。应用最小二乘法拟合曲线法对信号进行分析,得到其幅值相位表见表2。
由表可以看出,在含突变信号的谐波间谐波的检测中,该方法可以准确检测出频率,对于幅值和相位角的检测存在很小的误差。由傅里叶变换理论可知,对于单位冲激信号其频谱等于常数,也就是说,在整个频率范围内频谱函数是均匀分布的。对于矩形脉冲信号、其频谱以Sa(■)的规律变化(其中τ为脉冲宽度),分布在无限的频率范围上。结合最小二乘法原理可知,在谐波间谐波的检测中会存在较小的误差。
4.3 实际应用中典型信号的检测
仿真信号实例x(t)来源于文献[13],其表达式为
x(t)=15×■sin(2πf1t+θ1)+9.8×■sin(2πf2t+θ2)+
12×■sin(2πf3t+θ3)(12)
其中f1、 f2、 f3的頻率依次为250、287、300 Hz,初相角θ1、θ2、θ3依次为0°、90°、0°。
在该文献中,利用国标GB/T 17626.7——2008[3]与标准IEC 61000-4-7[4]介绍的方法,测量误差会超出国家标准要求的不大于5%的允许范围,不能得到准确的测量结果,方法失效。
利用本文介绍的方法,设置采样频率为1 000 Hz,采样点数为1 000,时间窗口的宽度为1 s。检测谐波间谐波分量的频率范围设置为1~400 Hz,频率分辨率为1 Hz(即式(7)中的ω=2π)。满足采样定理以及数据区间的长度为2π的整数倍。应用最小二乘法拟合曲线法对信号进行分析,得到其幅值相位表见表3。
由表可以看出该方法可以精确地检测出谐波与间谐波的频率、幅值、相位角。
通过对该方法的数学理论和工程应用的论证,以及由上述典型信号的仿真可以看出,在满足采样定理以及数据区间的长度为2π的整数倍时,对于需要较精确测量谐波间谐波频率、幅值、相位角的场合,该方法具有明显的实用价值。需要说明的是:在应用该方法时,对数据区间的长度提出了一定的限制要求,要求的数据窗口的长度较长,这是该方法在处理高精度要求的工程问题时一个瑕疵。关于在较短的时间窗进行处理将是今后的研究方向之一。
5 结束语
本文提出了一种谐波间谐波的检测方法:用最小平方三角逼近多项式逼近被测信号进行谐波间谐波的检测。在满足采样定理以及数据区间的长度为2π的整数倍时,通过利用函数族{1,cosx,sinx,…,cosnx,sinnx}在区间[0,2π]上的正交性,理论上论证了该方法的有效性。仿真实验表明,在满足理论要求的条件下,实际应用中该方法可以准确地检测出谐波间谐波的频率、幅值、相位角。与其他文献介绍的方法相比,该方法在求解精度上具有明显的优势。
参考文献
[1] 于振国. 火灾触电的隐形恶魔-电网内的谐波电流[J]. 安全与电磁兼容,2013(4):9-10.
[2] 于振国. 谐波电流的危害[J]. 家电科技,2009(15):52.
[3] 电磁兼容 试验和测量技术供电系统及所连设备谐波、谐间波的测量和测量仪器导则:GB/T 17626.7—2008[S]. 北京:中国标准出版社,2008.
[4] Electromagnetic compatibility(EMC), part 4-7: testing and measurement techniques-general guide on harmonics and interharmonics measurements and instrumentation,for power supply systems and equipment connected thereto:IEC 61000-4-7—2009[S]. 2009.
[5] 杜天军,陈光,雷勇. 基于混叠补偿小波变换的电力系统谐波检测方法[J]. 中国电机工程学报,2005(3):56-61.
[6] 陈长升,黄险峰. 基于小波变换抗混叠谐波检测的一种新方法[J]. 电力系统保护与控制,2008(23):23-26.
[7] 唐蕾,陈维荣. 瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析[J]. 电网技术,2008(5):66-69.
[8] 蔡瑾. 人工神经网络在电力系统谐波分析中的应用[J]. 中国科技信息,2012(4):40-41.
[9] 李庆扬,王能超,易大义. 数值分析[M]. 4版. 武汉:华中科技大学出版社,2006:64-65,68-69,192-193.
[10] 曹健,林涛,张蔓,等. 电力系统间谐波检测方法[J]. 高电压技术,2008(8):1745-1750.
[11] 廖晓文,刘桂雄,潘云飞. 一种高精度多路脉冲计数补偿方法[J]. 电子测量与仪器学报,2015,29(7):1074-1079.
[12] 扈罗全,向霞. 型式试验条件对吸尘器谐波电流的影响[J].苏州大学学报(工科版),2010(1):1-6.
[13] 侯立峰,黄纯,李波,等. 基于中国国家标准和IEC标准的谐波及间谐波测量方法[J]. 电网技术,2010(80:46-51.
(编辑:刘杨)

