四边形添辅助线审题的教学实践与反思

浙江省绍兴市越城区马山中学　陶苗娟



四边形添辅助线审题的教学实践与反思

浙江省绍兴市越城区马山中学陶苗娟

添辅助线解几何题是几何教学的一部分，也是几何教学的重难点所在。学生对几何基本说理过程的掌握存在一定困难。学生达到准确添辅助线解题的程度，显得难上加难。因而，部分学生对几何产生畏难情绪。教师在教学中应帮助学生建立信心，使学生仔细审题，充分利用已知条件或图形隐含信息找到正确的添辅助线方法，使学生形成正确的解题思路。

四边形 审题 添辅助线 线段相等

解几何题时，学生有正确的思路是解决问题的关键。解题思路与审题息息相关，特别是部分添加辅助线的题目，辅助线添对后题目就豁然开朗，辅助线找不到或者添错了，不仅解不出题目，还会对解题形成干扰。通过添辅助线，图形的性质得以显现，分散的条件得以集中，将新问题转化为旧问题。几何证题中，辅助线有桥梁和化难为易的作用。

实际教学中经常碰到的现象是，学生将苦思半天想不出的问题拿来请教教师，教师帮助学生找到关键条件稍加点拨或帮助，学生理清思路添加辅助线后恍然大悟。究其原因是学生没有养成仔细审题的良好习惯，缺少解几何题的方式方法。

学生对几何题存在畏难情绪的原因包括：一方面是几何说理过程写不清，另一方面是解题时难以形成思路，对已知条件如何有序组合、应用存在困难。特别是普遍条件缺少时，学生不会应用图形的特征添线、找线，常走弯路而不知及时回头修改，使解题陷入困境，使几何成为学生头痛的学科。教师要帮助学生自我点拨，掌握解几何题的方法与技巧，找到解题突破口，用正确的方法找到该添的线，掌握一定的审题技巧，形成解题思路。

在《特殊平行四边形》一章中有通过添辅助线证明两条线段相等习题。笔者从课本上的一道作业题说起，分析教学中教师如何帮助学生使用问题探究的方式，有效、快速地找到辅助线，使学生在审题过程中碰到问题及时反省，形成正确的解题思路。

已知：如图，在正方形ABCD中，E、F分别在AD、DC上，且DE=DF，BM⊥EF于M，求证：ME=MF。

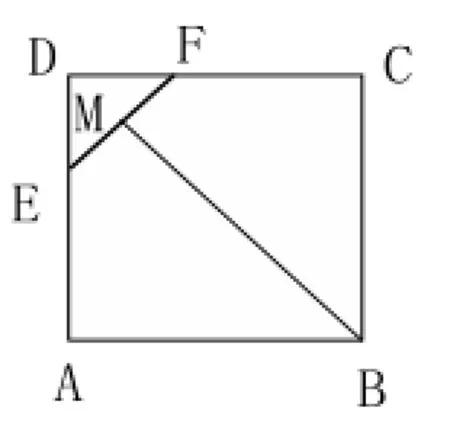
问题分析：练习过程中，笔者发现部分学生添辅助线时连接DM或延长BM，利用等腰三角形“三线合一”的性质说明EM=MF。这样做忽略了连接DM后，DM与EF是否垂直；忽略了延长BM后，BM的延长线是否经过点D。学生对添加的辅助线没有进行深入思考，无法继续解题。笔者设计以下问题启发学生，帮助学生找到正确的添辅助线的方法。

问题1：证明两条线段相等有哪些方法？

生答：全等三角形的对应边相等；等腰三角形两腰相等，等边三角形三边相等，在同一三角形中等角对等边，三线合一；中垂线上一点到线段两端的距离相等；角平分线上一点到角两边的距离相等；线段中点；平行四边形的对边相等，菱形、正方形四边相等；矩形对角线相等；平行线之间的距离相等；等量代换；三角形中位线等于第三边一半；直角三角形斜边上的中线等于斜边的一半；30°角所对直角边等于斜边的一半。

问题2：证明两条线段相等有很多方法，在具体题目中选择哪种方法进行证明？同学们在解题时会根据什么选择方法？

生答：结合已知条件，根据条件的提示选择方法；根据图形形状选择方法。

问题3：结合以前的解题经验，同学们能举例说明吗？

生答：如果条件中有中点，选中位线，中线或三线合一的方法证明；如果条件中有平行四边形，应用平行四边形的性质证明；如果有两个三角形，证明两个三角形全等如果出现一个三角形，就证明此三角形为等腰三角形。

问题4：本题中证明EM=MF，结合条件BM⊥EF，你会选择哪种方法证明？

生答：利用三线合一的性质证EM=MF；利用全等性质证EM=MF。

问题5（针对第一种方法设计）：三线合一的前提条件是等腰三角形，图中有这样的等腰三角形吗？你认为在△DEF中添辅助线能达到目的吗？如果不行，如何构造等腰三角形？

问题分析：受图形暗示及思维定式影响，如果出现两个三角形，学生解题时会用全等证明线段相等。因此，大部分学生证明△ABE≌△ADF。解题过程中，学生容易找到证明全等的两个条件AB=AD，∠B=∠D，但证明△ABE≌△ADF的第三个条件很难找到。学生用已知条件很难转化出边相等或角相等，解题陷入困境。

面对学生的错误选择，笔者在教学中设计以下问题帮助学生正确添加辅助线。

问题1：两条线段出现在两个三角形中，证两条线段相等，我们往往考虑证明这两个三角形全等，但有时全等的条件不容易找甚至找不到，我们怎么办？

生答：转换思路，想其他办法。

问题2：四边形问题一般可转换为三角形问题，结合菱形性质，当菱形中有一个角为60°时，同学们可得到什么结论？

生答：得到等边三角形。

问题3：四边形转化为三角形的问题中，我们常用的添辅助线的方法是什么？同学们想到怎么添辅助线了吗？

生答：连对角线，连接AC。

教学反思：结合学生产生的思维困惑或理解偏差，笔者从学生需要出发，帮助学生找出问题成因，设计一系列具有针对性的问题，启迪学生思维，深化问题本质，帮助学生理顺解题思路，解决困惑，使学生学会仔细审题，找到正确的辅助线。

笔者通过问题设计引导学生进行发散思维，寻找多种方法解答同一题目并进行方法比较。引导学生对问题进行分类思考，探究条件改变的情况下结论之间的关系。

现代学习方式强调教师通过问题引领学生学习，同时通过学习生成问题，即课堂教学要有“问题”意识。教师在课堂教学中设计问题、提出问题固然重要，但更要关注来自学生的问题，使学生在发现问题、解决问题中成为学习的主人。

教师要鼓励学生出现学习困惑时问问自己为什么卡住，有哪些地方没弄明白，碰到一个问题有哪些解决方法等。解题中，学生形成思维障碍的主要原因是学生现有的认知水平不能顺应教学内容，造成知识运用上脱节。因此，教师要培养学生树立问题意识，用问题深化知识发生和发展的关联，拓展学生思维，提升学生的探究意识，使学生顺利理解知识、消除困惑、掌握基本解题技能，使问题成为学生探究性学习的向导。

通过不断尝试与探究，学生明白添辅助线是一项难度很大的技巧，出现错误并不可怕，关键要懂得及时改正。问题探究的过程中，学生学会自己提问、自己解答，这是解决问题的最佳方法。

添辅助线解几何题时除凭借直觉思维、经验之外，学生还可应用已知条件的提示或者结论对题目进行逻辑思维与深度思维。学生需要多次尝试才能成功添加辅助线，寻找辅助线的过程中，学生思维得到训练、发展和碰撞。学生通过不断尝试，仔细审题，自我探究，形成解决问题的方法。

课堂实践的目的是指导学生掌握审题技巧。教师引导学生少走弯路，及时纠正错误。面对错误思路，学生要舍得花时间分析错误产生的原因，自我交流、思考、总结的过程就是学生思维火花碰撞的过程，是学生自主构建知识网络的过程。

课堂上，教师应有意识地引导与训练学生，有利于学生养成良好的审题习惯，有利于学生掌握问题探究、寻找辅助线的方法，使不同学生得到不同发展。

学生需要对题目条件进行深入思考与挖掘，需要锲而不舍的探究精神及一定量的练习。

［1］倪小芳.巧添辅助线证几何题［J］.数理化学习（初中版），2013

［2］党晓燕.找准学生“发展区”创生教学“生长点”——对高三数学教学的几点体会［J］.宁夏教育科研，2012

ISSN2095-6711/Z01-2016-06-0187