旋风分离器旋进涡核的大涡数值模拟

龙薪羽， 刘根凡， 毛　锐， 王平平

(华中科技大学 能源与动力工程学院， 湖北 武汉 430074)



旋风分离器旋进涡核的大涡数值模拟

龙薪羽， 刘根凡， 毛锐， 王平平

(华中科技大学 能源与动力工程学院， 湖北 武汉 430074)

摘要：基于Smagorinsky-Lilly亚格子模型，将多面体网格应用于旋风分离器的大涡模拟，得到其平均流场和速度场脉动，并与实验值对比。对速度脉动进行快速傅里叶变换，以此探索旋进涡核的影响范围；通过涡速度云图，观察涡核中心的瞬态变化。结果表明，基于多面体网格的大涡模拟可以有效求解旋风分离器平均流场和速度脉动；斯特劳哈尔数的计算值为0.51，与实验值0.49非常接近。旋进涡核致使切向、轴向和径向的速度分量存在一致的主频；不考虑湍流边界层，旋进涡核存在于整个分离空间，且大部分位置的主频皆为11.54 Hz；旋进涡核中心在一定范围内围绕几何轴旋转，且旋转方向同主流方向一致。

关键词：旋风分离器； 旋进涡核(PVC)； 大涡模拟(LES)

旋风分离器由于结构简单、投资及运行成本低、分离效率适中等优势，广泛应用于工业除尘[1]。尽管其结构简单，但是旋风分离器的内部流场异常复杂。不仅存在着三维强旋流场，且旋流在自转的同时，其内旋流中心也时刻在发生变化，形成了所谓的旋进涡核[2](Processing vortex core，PVC)。研究表明，旋进涡核可能会导致压力场出现较大波动，进而引起旋风分离器的机械故障[3]，应引起足够的重视。

数值模拟是研究旋风分离器的重要手段。已有学者发现，雷诺平均模型(RANS)中，只有规避了各向同性涡旋黏性假设的雷诺应力模型(RSM)才可以准确地计算其平均流场[4-5]。但是对于旋进涡核的求解，RSM模型仍存在较大误差。这主要体现在速度脉动和旋进涡核主频的计算上[6-8]，而速度脉动是影响小颗粒分离效率的重要因素[9-10]。Derksen[11-12]、Gronald等[13]对旋风分离器进行大涡模拟(Large eddy simulation，LES)计算，得到了比较准确的平均流场和速度场脉动，并对旋进涡核进行了部分分析。但是这些分析只局限于流场的单个点，而没有对全局流场进行旋进涡核分析。

笔者首次将多面体网格作为离散网格，应用Smagorinsky-Lilly亚格子模型对旋风分离器进行了大涡模拟数值计算，并结合相关实验，详细分析了旋进涡核对整个流场的影响，进一步完善了对旋进涡核的认识。

1　LES模型控制方程

湍流流场中起主导作用的是大尺度旋涡，小尺度旋涡主要引起湍流动量的扩散。大涡模拟法的本质为用非稳态的Navier-Stokes方程(N-S方程)直接模拟大尺度旋涡运动，而通过模型模拟小尺度旋涡运动。

对于不可压缩的流动，LES模型控制方程[9,14]如式(1)、式(2)所示。

(1)

(2)

(3)

(4)

(5)

2　旋风分离器物理模型和数值计算方法

旋风分离器结构尺寸来源于Derksen[12]的实验模型。坐标原点位于底部圆心，数据测点沿z轴方向，x、y和z方向分别对应测点的轴向、切向和径向，筒径D为100mm，主要结构尺寸和局部网格如图1所示。入口速度uin为2.26m/s，对应的入口雷诺数为Re=uinD/v=1.54×104，几何旋流数Sw用式(6)表示，大小为2.08。

(6)

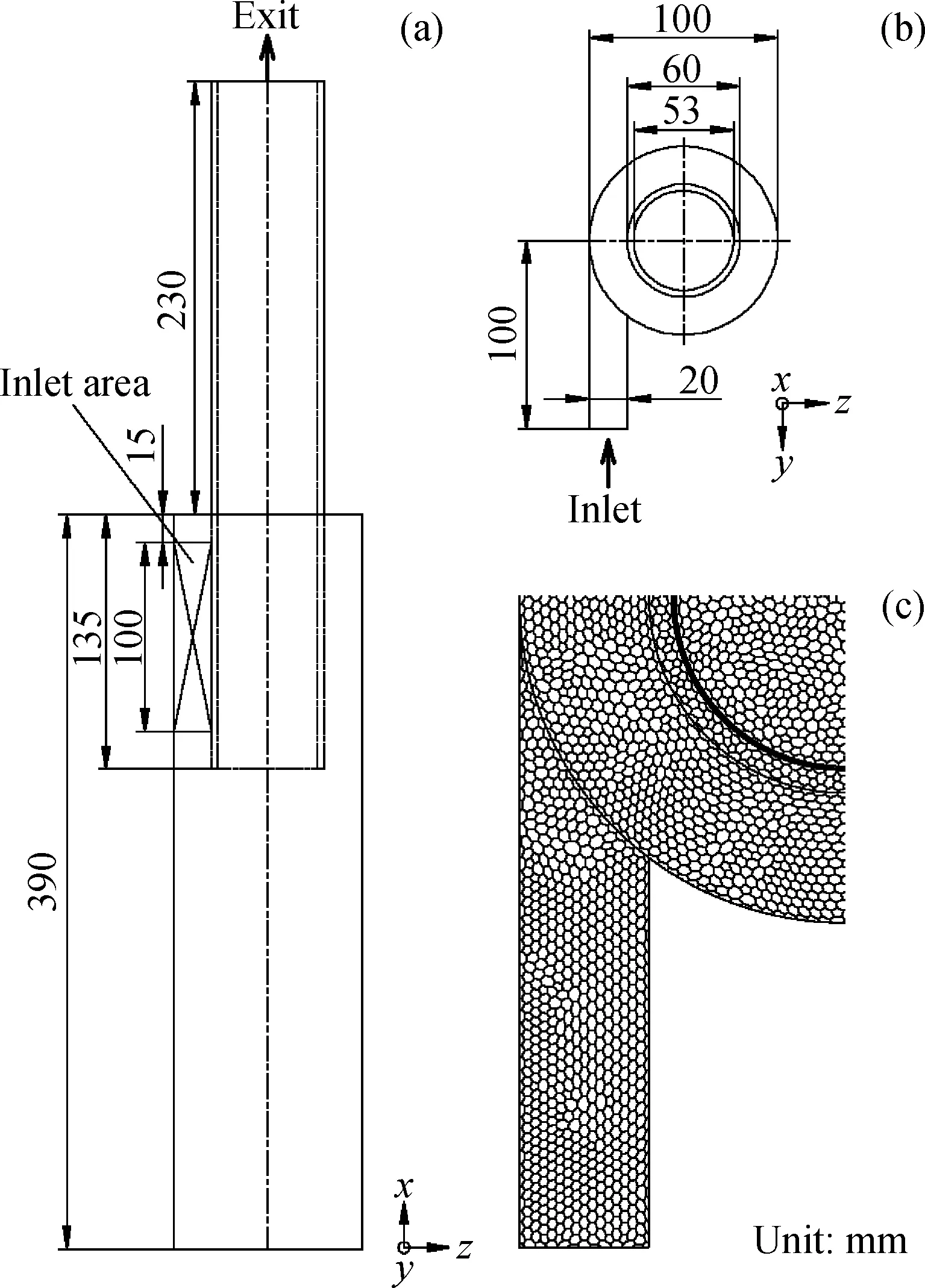
图1　旋风分离器结构和局部网格图Fig.1　Structure and local grid of cyclone separator (a) Front view; (b) Top view; (c) Local grid of top view

计算采用所有壁面加密处理的多面体网格，并经网格无关性验证，发现网格数为683873(节点数3542841)时已获得网格无关解。入口边界为均匀速度入口，速率为2.26 m/s；出口为自由出流边界，假设所有流动变量在出口法向方向的梯度为零。压力-速度耦合算法为SIMPLEC算法，控制方程离散格式选用中心差分格式。以RSM模型的定长计算结果作为初解，而后转为LES模型计算。时间步长为5×10-4s，全局最大网格库朗数小于11，时间步长的设置满足要求(见文献[14])。各变量的收敛精度为10-5，当出口静压等变量呈谐波变化时开始统计，统计时间为80D/uin=3.54 s。

3　结果与讨论

3.1旋风分离器计算结果验证

3.1.1旋风分离器平均流场验证

选取旋风分离器的水平面x=89 mm进行计算模型准确性的验证，结果示于图2。由图2可知，LES模型计算的平均流场与实验值吻合度非常高，二者都呈现出非对称的流场结构，这主要是由单向气流入口所致[15]。切向速度的“兰金涡”特征以及轴向速度的“驼峰”特征都得到了很好的捕捉。但中心区域流场计算的准确性要稍低于两侧区域，这也侧面反映了中心区域流场更为复杂。边界层附近的流动特征在实验中难以测量，而通过数值计算可以得到体现，如靠近壁面附近时，发现切向速度和轴向速度皆急剧下降并趋于零，而且速度梯度明显增加。

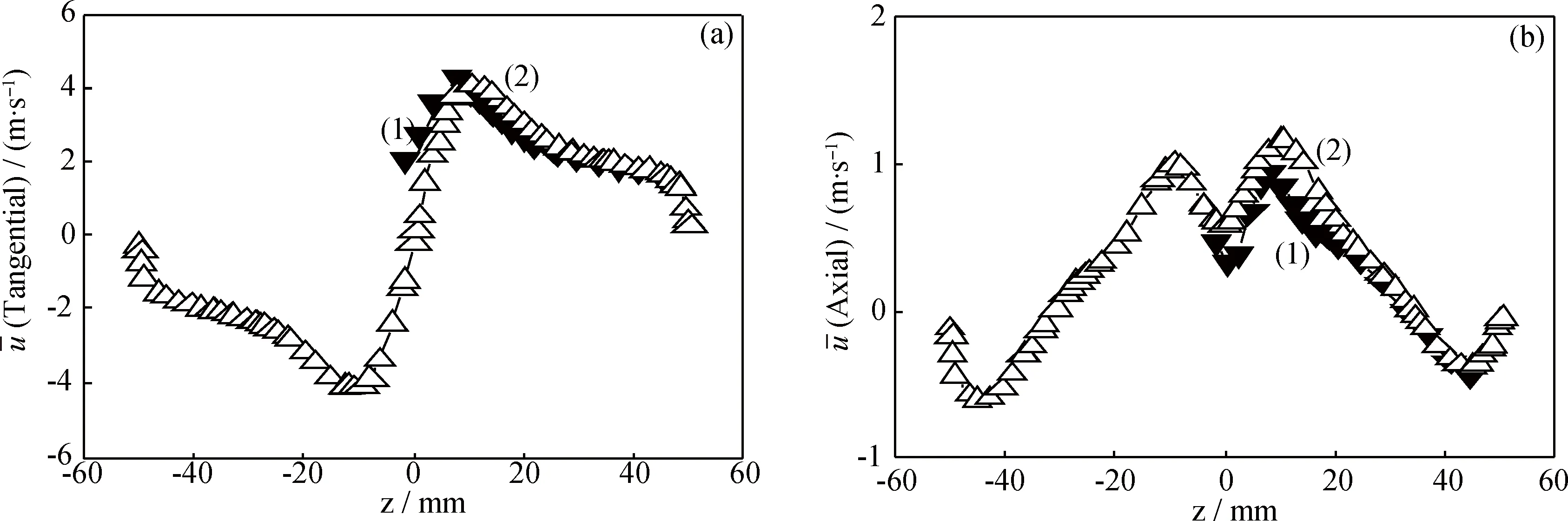
图2　旋风分离器内水平面x=89 mm处平均速度径向分布Fig.2　Radial profiles of average velocity in the horizontal plane at x=89 mm in cyclone separator (1) Experimental data; (2) Calculated data (a) Tangential velocity; (b) Axial velocity

3.1.2旋风分离器速度脉动验证

速度脉动的平均值为零，一般用速度脉动的均方根(RMS)来表示速度脉动，称为RMS速度，如式(7)所示。

(7)

图3为旋风分离器内水平面x=89 mm处RMS速度的径向分布。由图3可发现，RMS速度的实验值和计算值比较接近，分布趋势也非常一致，如中心区域的RMS速度要明显大于两侧区域RMS速度。这是由于旋进涡核中心主要在旋风分离器几何中心附近游弋所致(下文有详细分析)，而两侧区域的脉动则与湍流场本身的脉动有关。无论是切向速度还是轴向速度，平均速度出现极值的径向位置，其附近的速度脉动皆会出现极小值，如在切向速度“准自由涡”与“准强制涡”的分界线位置以及轴向速度的中心位置，Gronald等[13]也有相同发现，这说明速度脉动同时也受到平均速度梯度的影响。通过计算可知，在接近壁面的过程中，速度脉动还出现了轻微增加的趋势，该趋势是因为受到筒壁干扰后速度梯度显著增加所致。

图3　旋风分离器内水平面x=89 mm处RMS速度的径向分布Fig.3　Radial profiles of RMS velocity in the horizontal plane at x=89 mm in cyclone separator (1) Experimental data; (2) Calculated data (a) Tangential RMS velocity; (b) Axial RMS velocity

3.2旋风分离器内旋进涡核分析

3.2.1旋风分离器内旋进涡核(PVC)的存在

图4是在点(190,0,0)处z方向的速度脉动分量随时间的变化值(纵坐标为瞬时速率与平均速率的差值)，对其进行快速傅里叶变换(FFT)即可得相应的功率谱密度(Power spectral density，PSD)，纵坐标为速度脉动平方的频谱，如图5(a)所示。由图5(a)可知，主频f为11.54 Hz，对应的斯特劳哈尔数为St=fD/uin=0.51，与实验值(St=0.49)非常接近；同时该主频也证实了旋进涡核(PVC)的存在(入口段的实验值和计算值都没有主频)。

图4　在点(190,0,0)处z方向的速度脉动分量时序图Fig.4　Time series of the fluctuating velocity component in the z-direction at point of (190,0,0)

利用相同的方法得到在点(190,0,0)处x方向和y方向速度脉动分量的频谱图，如图5(b)和(c)所示。由图5可知，3个分速度方向具有相同的主频值，且y、z方向主频对应的幅值非常相近，而x方向对应的幅值要低于其他两个方向。这是因为，对于速度脉动的功率谱密度图而言，其关系曲线下的面积就是速度脉动的均方值即均方根值的平方。图6为旋风分离器内x=190 mm处水平面内不同方向的RMS速度径向分布。由图6可见，x方向速度脉动在中心区域的均方根值要明显低于y、z两个方向，这就导致x方向的频谱幅值要低于另外两个方向(以下分析，以z方向的主频作为PVC的主频)。同时由图6还可发现，3个方向的速度脉动相差较大，说明了流动的各向异性。

图5　点(190,0,0)在x、y、z方向的速度脉动 分量对应的频谱图Fig.5　Signal spectra of the fluctuating velocity component in the x, y and z-direction at point of (190,0,0) (a) z-Direction; (b) x-Direction; (c) y-Direction

3.2.2旋风分离器内旋进涡核的影响范围

不考虑壁面边界层区域，对水平面x=190 mm沿z轴方向的一系列数据点进行z方向速度分量的监测。通过对速度脉动的FFT分析，发现在整个径向方向均存在着大小为11.54 Hz的主频。这说明旋进涡核不仅影响着中心区域，还影响整个径向区域。

对旋风分离器中心轴上的多个位置进行旋进涡核主频分析，结果如图7所示。由图7可见，除了靠近旋风分离器底部附近的旋进涡核频率发生了变化，其他位置的主频均为11.54 Hz。同时，在x=120 mm水平面除了有11.54 Hz的主频，还出现了10.10 Hz的次主频，说明旋进涡核影响旋风分离器分离空间的整个纵向区域，并且气流在旋风分离器底部的折返还会加剧旋进涡核的复杂性，而该区域也是灰尘极易被二次夹带的区域。

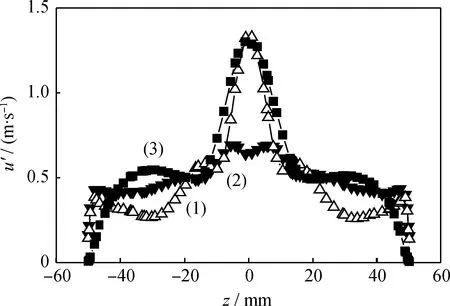
图6　旋风分离器内x=190 mm处水平面内不同方向的 RMS速度径向分布Fig.6　Radial profiles of RMS velocity of different directions at x=190 mm in cyclone separator (1) x-Direction; (2) y-Direction; (3) z-Direction

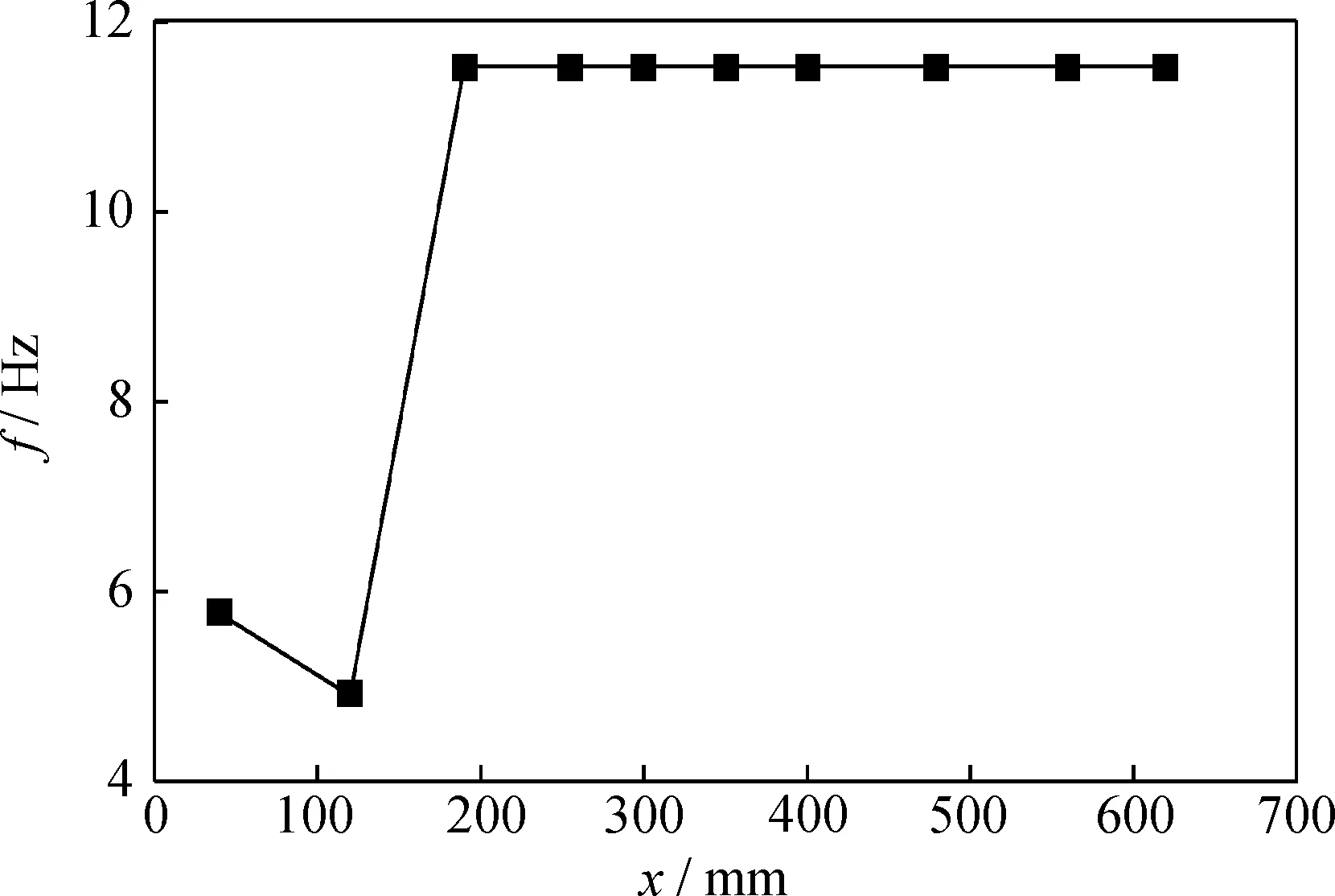
图7　旋风分离器内旋进涡核(PVC)沿着x方向的主频变化Fig.7　Frequency charges of PVC along x-direction in cyclone separator

3.3旋风分离器内旋进涡核的具体表现

笔者采用涡速度(Vortex velocity，切向速度和径向速度的矢量和)来表征旋进涡核，并将水平面的涡速度最小值视作涡核中心。

图8为不同水平面内时间平均的旋进涡核中心与几何中心的距离。在图8中最大偏移值(约0.025D)出现在水平面x=150 mm处，同时在旋风分离器底部以及升气管入口下游附近都出现了较大的偏移量。这主要是因为气流与旋风分离器底部的撞击以及气流进入升气管后的流道收缩，均加剧了旋进涡核的摆动，并对颗粒的分离产生不利影响。

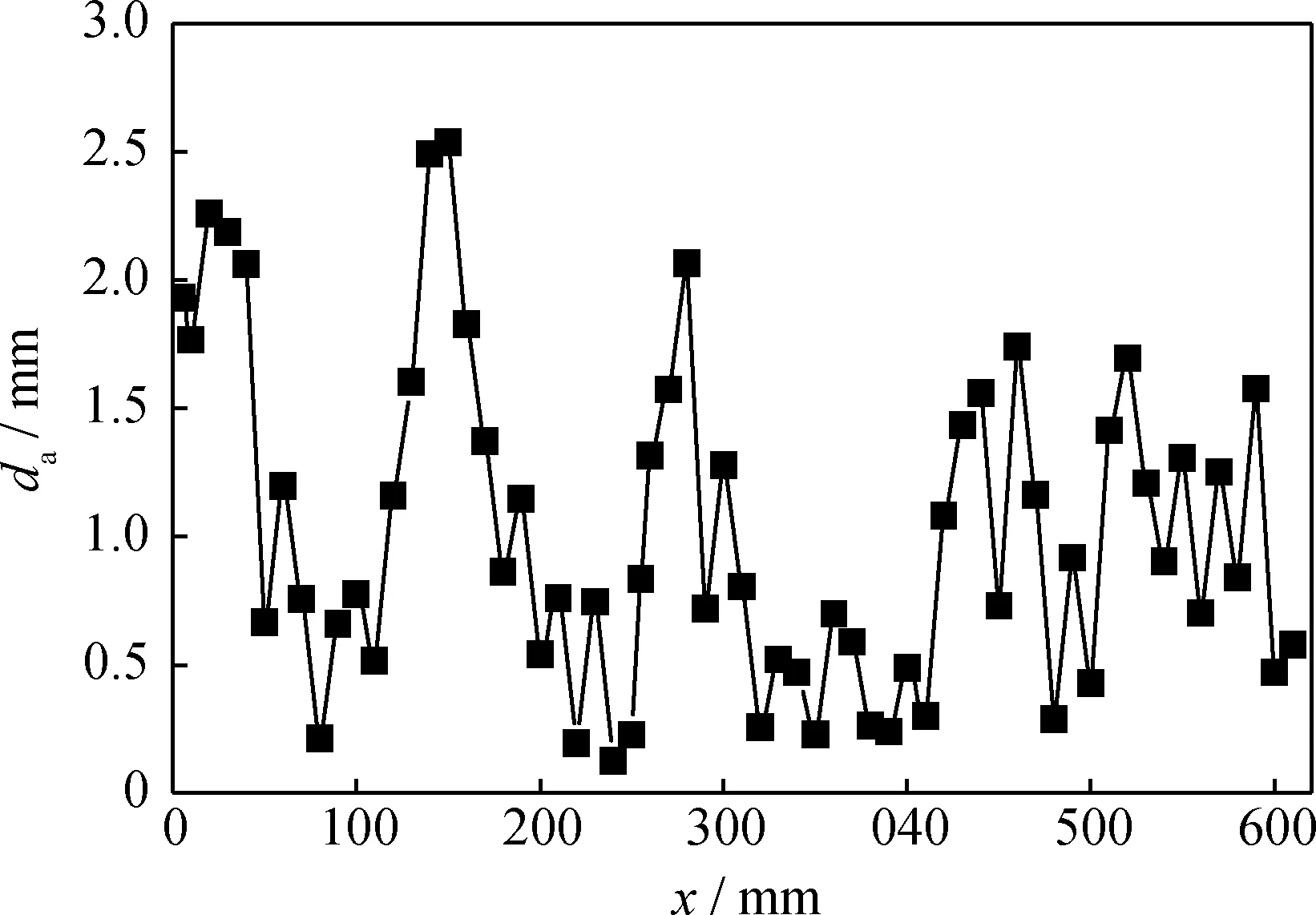
图8　旋风分离器内时间平均的旋进涡核中心 偏离几何中心的距离Fig.8　Distance between center of time average vortex-core and geometry center along x-direction in cyclone separator

图9反映了水平面x=190 mm的瞬态涡速度变化，图9(a)～(l)各云图之间的时间间隔为旋进涡核周期(1/11.54 Hz=0.0867 s)的1/10。由图9可知，旋进涡核中心绕几何中心顺时针旋转，且涡核中心的旋转方向与主流一致。尽管该平面时间平均的涡核中心距几何中心距离为0.0115D(见图8)，但是在瞬态流场分析中发现，其涡核中心偏移几何中心的最大距离达到了0.077D，这也使得更大区域的速度脉动得到了加强。同时涡核中心在一定范围内绕中心轴旋转，也解释了只有中心区域的速度脉动受到更大影响的原因。

图9　旋风分离器内水平面x=190 mm处 不同时刻的涡速度云图Fig.9　Vortex velocity magnitude contour at different time in the horizontal plane at x=190 mm in cyclone separatort/s: (a) 2.00000; (b) 2.00867; (c) 2.01734; (d) 2.02601; (e) 2.03468; (f) 2.04335; (g) 2.05202; (h) 2.06069; (i) 2.06936; (j) 2.07803; (k) 2.0867; (l) 2.09537

4　结　论

(1)采用Smagorinsky-Lilly亚格子模型，以多面体网格作为离散网格，对旋风分离器进行大涡模拟计算，得到与实验值非常吻合的平均流场和速度场脉动。捕捉到切向速度的“兰金涡”特征以及轴向速度的“驼峰”特征，尤其准确预测了RANS模型难以计算的速度脉动，证明本计算方法切实有效。

(2)对速度脉动进行快速傅里叶变换得到的主频证明了旋风分离器内旋进涡核的存在，计算得到的St数为0.51，与实验值0.49非常接近。同时，旋进涡核的存在使得在切向、轴向和径向发现相同的主频，但轴向对应的幅值要低于其他两个方向，这主要是因为轴向的速度脉动值比其他两个方向更低。

(3)不考虑壁面附近的边界层区域，整个旋风分离器分离空间都可以发现旋进涡核引起的主频。除了旋风分离器底部附近的主频不一致，其他区域的主频均为11.54 Hz，同时在底部区域的上部位置还发现了10.10 Hz的次主频，这间接反映了该区域的流场紊乱。

(4)旋进涡核中心在旋风分离器底部以及升气管下游区域的摆动比较剧烈，这些区域也是颗粒极易发生逃逸的区域，在旋风分离器的设计中应当引起重视。

(5)涡核中心在一定范围内绕着几何中心移动，这使得只有中心区域的速度脉动得到了增强，并且旋转方向同主流方向一致。

符号说明：

Ain——旋风分离器矩形入口的面积，mm2；

Cs——常数0.1；

d——距离最近壁面的长度，m；

da——涡核中心与几何中心的距离，mm；

de——旋风分离器升气管直径，mm；

D——旋风分离器筒体直径，mm；

f——频率，s-1；

Ls——网格的混合长度，m；

N——采样数；

Re——入口雷诺数；

St——斯特劳哈尔数；

Sw——几何旋流数；

t——时间，s；

ud——瞬时速率与平均速率的差值，m/s；

ui——瞬时速度，m/s；

uin——入口速度，m/s；

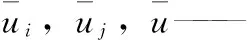
uv——涡速度，m/s；

u′——速度脉动，m/s；

v——运动黏度，m2/s；

V——计算网格的体积，m3；

xi，xj——通用坐标，m；

δij——克罗内克符号；

κ——von Krmn常数；

μ——动力黏度，N·s/m2；

μt——亚格子湍流黏性力，kg/(m·s)；

ρ——气流密度，kg/m3；

τij——亚格子应力，kg/(m·s2)；

τkk——亚格力应力的各项同性部分，kg/(m·s2)。

参考文献

[1] 吴小林，申屠进华，姬忠礼.PV型旋风分离器内三维流场的数值模拟[J].石油学报(石油加工)，2003， 19(5): 74-79.(WU Xiaolin, SHENTU Jinhua, JI Zhongli. Numerical simulation of three-dimension flow filed in a PV type cyclone[J].Acta Petrolei Sinica (Petroleum Processing Section)， 2003， 19(5): 74-79.)

[2] 元少昀，吴小林，时铭显.旋风分离器内旋进涡核的实验研究[J].化工机械，1999， 26(5): 249-252.(YUAN Shaoyun, WU Xiaolin, SHI Mingxian. Experimental investigations on the precessing vortex core(PVC) in cyclones[J].Chemical Engineering & Machinery， 1999， 26(5): 249-252.)

[3] GRIFFITHS A J, YAZDABADI P A, SYRED N. Alternate eddy shedding set up by the nonaxisymmetric recirculation zone at the exhaust of a cyclone dust separator[J].Journal of Fluids Engineering， 1998, 120(1): 193-199.

[4] HOEKSTRA A J, DERKSEN J J, VAN DEN AKKER H. An experimental and numerical study of turbulent swirling flow in gas cyclones[J].Chemical Engineering Science， 1999, 54(13): 2055-2065.

[5] 王海刚，刘石.不同湍流模型在旋风分离器三维数值模拟中的应用和比较[J].热能动力工程， 2003， 14(4): 337-342.(WANG Haigang, LIU Shi. Application and comparison of different turbulence models in the three-dimensional numerical simulation of cyclone separators[J].Journal of Engineering for Thermal Energy and Power， 2003， 14(4): 337-342.)

[6] HOEKSTRA A J. Gas flow field and collection efficiency of cyclone separators[D].TU Delft： Delft University of Technology, 2000.

[7] SHUKLA S K, SHUKLA P, GHOSH P. Evaluation of numerical schemes using different simulation methods for the continuous phase modeling of cyclone separators[J].Advanced Powder Technology，2011, 22(2): 209-219.

[8] 吴小林，熊至宜，姬忠礼，等.旋风分离器旋进涡核的数值模拟[J].化工学报，2007， 58(2): 383-390.(WU Xiaolin, XIONG Zhiyi, JI Zhongli, et al. Numerical simulation of precessing vortex core in cyclone separator[J].Journal of Chemical Industry and Engineering， 2007， 58(2): 383-390.)

[9] SHUKLA S K, SHUKLA P, GHOSH P. The effect of modeling of velocity fluctuations on prediction of collection efficiency of cyclone separators[J].Applied Mathematical Modelling， 2013, 37(8): 5774-5789.

[10] SALVO R V, SOUZA F J, MARTINS D. Simulation of the gas-particle flow in a cyclone separator[J/OL].ICHMT Digital Library Online. 2012.

[11] DERKSEN J J. Separation performance predictions of a Stairmand high-efficiency cyclone[J].AIChE Journal， 2003, 49(6): 1359-1371.

[12] DERKSEN J J, VAN DEN AKKER H. Simulation of vortex core precession in a reverse-flow cyclone[J].AIChE Journal， 2000, 46(7): 1317-1331.

[13] GRONALD G, DERKSEN J J. Simulating turbulent swirling flow in a gas cyclone: A comparison of various modeling approaches[J].Powder Technology， 2011, 205(1-3): 160-171.

[14] Fluent, Inc. Fluent 6.3 Users’ Guide[M]. New Hampshire： America: Fluent Inc, 2006: 12-51-12-53.

[15] 王江云，毛羽，王娟.单入口双进气道旋风分离器内流体的流动特性[J].石油学报(石油加工)， 2011, 27(5): 780-786. (WANG Jiangyun, MAO Yu, WANG Juan. Flow characteristic in a single inlet cyclone separator with double passage[J].Acta Petrolei Sinica(Petroleum Processing Section)， 2011, 27(5): 780-786.)

收稿日期：2015-05-22

基金项目：煤燃烧国家重点实验室开放基金项目(FSKLCC1207)资助

文章编号：1001-8719(2016)04-0734-07

中图分类号：TQ051.8

文献标识码：A

doi:10.3969/j.issn.1001-8719.2016.04.011

Large Eddy Simulation of Vortex Core Processing in Cyclone Separator

LONG Xinyu， LIU Genfan， MAO Rui， WANG Pingping

(SchoolofEnergyandPowerEngineering,HuazhongUniversityofScienceandTechnology,Wuhan430074,China)

Abstract：Based on Smagorinsky-Lilly Subgrid-Scale model, polyhedral mesh was employed in large eddy simulation of a cyclone separator. The average flow profiles and velocity fluctuations were obtained and compared with experimental observations. In order to analyze the scope of impact of processing vortex core (PVC), fast Fouier transform technique was applied to velocity fluctuations. Instantaneous changes of processional center of the core were investigated by vortex velocity contours. The obtained results indicated that the large eddy simulation with polyhedral mesh had a good performance in the simulation of the cyclone about average flow field and velocity fluctuation. The Strouhal number associated with the simulated PVC was 0.51, close to experimental value of 0.49. By the way, because of the existence of PVC, the tangential, the axial and radial components of velocity shared the same dominant frequency. PVC existed in all the separation region without considering turbulent boundary layer, with the dominant frequency of 11.54 Hz at most positions. In a certain range the processional center of the core rotated around the geometrical axis of the cyclone, with the rotation direction being consistent with the mainstream direction.

Key words：cyclone; processing vortex core (PVC); large eddy simulation (LES)

第一作者： 龙薪羽，男，硕士，从事气-固两相流及旋转机械的数值模拟研究

通讯联系人： 刘根凡，男，教授，硕士，从事气-固分离装置方面的研究；Tel：027-87556354；E-mail：liugenfan@hust.edu.cn