关于平面解析几何复习中学生运算能力培养的几点思考

李仲名（江苏省昆山震川高级中学）

关于平面解析几何复习中学生运算能力培养的几点思考

李仲名
（江苏省昆山震川高级中学）

一、问题的提出

平面解析几何（以下简称“解几”）是高考考查的重点内容，高考中解几的得分常常不尽如人意。学生普遍认为解几难，难在繁琐的运算。因此，提高解几的得分，运算能力是关键。笔者对此做了一些有益的探索。

二、对运算能力的认识

一些师生认为运算能力就是“死算”的能力，这样的理解是片面的。笔者认为：运算能力是“想”指导下的“算”；既检验学生的知识水平，又考验他们的心理和意志。算，包含了算法、算理、策略，需要思考和甄别。不合理的算法导致繁琐，不能直击量与量之间的联系，最终很容易放弃。因此，学生的运算能力，最终取决于学生的思维能力。

三、如何培养学生的运算能力

1.提高认识

提高学生的运算能力，就要对解几的计算有正确的认识：解几是用代数的方法研究几何问题，运算是不可避免的，出现一些复杂运算也很经常，培养学生的运算能力是解几教学的一项重要任务。算是我们学科教学的要求，也是我们学生应具备的一种能力，因此，要让学生明白：不能怕算，要重视算。

2.重视基础知识、基本方法的复习

提高学生的运算能力，着眼点还是要重视基础知识、基本方法。融会贯通了，才能为我们寻求合理简单的解法打下坚实的基础。例如：2011年江苏高考第（18）题：如图，在平面直角坐标系xOy中，M，N分别是椭圆的顶点，过坐标原点的直线交椭圆于P，A两点，其中点P在第一象限，过P作x轴的垂线，垂足为P，连接AC，并延长交椭圆于点B，设直线PA的斜率为k。

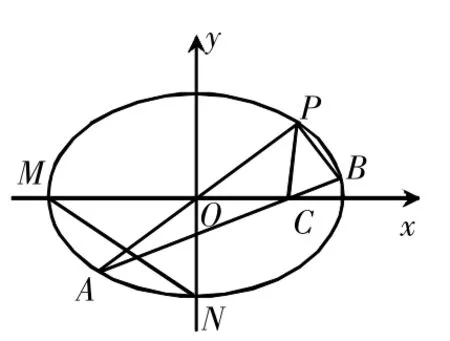
①当直线PA平分线段MN，求k的值；

②当k=2时，求点P到直线AB的距离d；

③对任意k＞0，求证：PA⊥PB。

本题的第③问意味深长，给了不同层次学生以不同的发挥空间。如果学生设出点P的坐标，由椭圆的对称性得出点A的坐标，由于点C是点P在x轴上的投影，因此，点C的坐标已知，从而直线AB的方程可得，用直线AB的方程与椭圆方程联立，可将点B的坐标计算出，从而可以证得kPA·kPB=-1，得到PA⊥PB。这一思路看似简单自然，但由于运算量很大，能够证得结果的学生少之又少。如果我们的学生能够充分利用椭圆的对称性，挖掘图形的几何特征，再利用“点差法”这种解决直线与椭圆的基本方法，就能很轻松地化解繁琐运算，获得问题的简捷解法。

设A（x1，y1），B（x2，y2），A，B中点N（x0，y0）则P（-x1，-y），C（-x1，0）

解几是代数与几何的结合体，既要重视代数的运算与推理，又要关注几何性质的应用。既要重视“死算”，又要重视“巧算”。但不管怎么算，都要以基础知识，基本方法为依托。因此，重视基础，打好基础，是提高解几运算能力的关键。

3.巧代换，妙转化

运算能力强不强，主要看学生对字母的运算，特别是涉及多元变量运算问题的处理和应变能力，能否化繁为简成为关键。我们看2012年的江苏高考第（19）题：如图，在平面直角坐标系xOy中，椭圆的左、右焦点分别为已知（1，e）和都在椭圆上，其中e为椭圆的离心率。

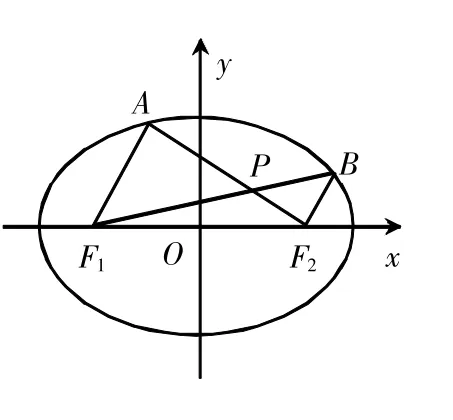
①求椭圆的离心率；

②设A，B是椭圆上位于x轴上方的两点，且直线AF1与直线BF2平行，AF2与BF1交于点P。

（ii）求证：PF1+PF2是定值。

以上解法中，我们在计算出左焦半径AF1后，没有重复解方程组求右焦半径BF2，而是用-m代换①式中的m，即为右焦半径的BF2长，代换思想的产生，取决于学生对椭圆几何性质的理解与应用。当然，如果学生能够延长AF1交椭圆于点B1，由椭圆的对称性知：线段BF2=B1F1将两条焦半径变成一条过右焦点的弦。利用焦半径公式问题转化为再利用韦达定理，问题很快获解。巧妙地将问题转化，化陌生为熟悉，避免了求交点坐标，从而减少了大量的繁琐运算。对理科学生，还可以通过建立极坐标系，将问题转化为，其中e，p为常数，解出cosθ，得到tanθ即为斜率。因此，巧妙代换，合理转化，也是提高学生运算能力的重要思想与途径。

4.复习建议

在解几的复习课上，要多给学生时间和空间，让学生多动笔，多思考，亲身经历求解过程。不要出现老师代替学生运算的现象。我们发现，解几复习课中，老师为了赶进度，往往分析一下解题的思路就把答案报给学生，这就是典型的老师代替学生运算的现象；加强算法、算理以及运算策略的指导，提高学生的运算求解能力；重视代数运算的同时，要注意对几何性质的挖掘，达到简化运算的目的；加强考试心理指导，培养学生意志品质。

总之，只要我们提高认识，打好基础，重视策略，学生运算能力的培养与提升就指日可待。

·编辑王团兰