“提取公因式法（1）”教学设计说明

沈艳秋（上海市普陀区曹杨中学附属学校）



“提取公因式法（1）”教学设计说明

沈艳秋（上海市普陀区曹杨中学附属学校）

摘要：以数的分解为起点，类比联想进行多项式因式分解的教学，引导学生将“数”的分解的学习经验迁移到“式”的分解中，经历概念发生、发展和形成的过程，最终使整个概念系统得以完备．通过“三问”驱动学生深入理解核心概念——因式分解，期盼学生真正理解因式分解的概念．

关键词：因式分解；由“数”及“式”；类比联想；“三问”驱动

内容与内容解析

因式分解是初中数学教学中最基本、最重要的内容之一，是整式的一种恒等变形，它与整式乘法互为逆变形．同时，因式分解又是由整式运算进入分式运算的学习过程中必需的知识技能准备，是接下来学习分式运算的重要基础．此外，因式分解在数学学科其他方面和一般科学研究中，也不乏它的应用．

本节课是上海教育出版社《义务教育教科书·数学》第九章第五节“因式分解”的第一课时，因此笔者将教学内容确定为两部分：一是因式、公因式、因式分解等有关概念，其中因式分解是核心概念．由于对公因式的理解，必须建立在其上位概念因式的基础上，因式是母概念，公因式是其子概念，因此补充了教材中没有出现的因式概念；二是因式分解的基本方法之一——提取公因式法．这部分内容是以“数”的分解为起点进行知识迁移，展现字母表示数、类比的数学思想，同时对运用不同形态的数学语言概括与表达，给出必要的规范．

目标与目标解析

基于对上述教学内容的思考，笔者将本节课的教学目标设置如下.

（1）通过类比因数、公因数、分解素因数，理解因式、公因式、因式分解等概念的意义；

（2）知道因式分解和整式乘法的互逆关系，初步掌握提取公因式法进行因式分解；

（3）感受字母表示数、类比等数学思想，提高运用数学语言概括与表达的能力.

学生由“数”及“式”地理解因式、公因式、因式分解等概念的意义，在这个过程中能够自然地感受到类比的数学思想，有充分的机会用数学语言进行概括和表达．对于因式分解的提取公因式法，本课时只要求初步掌握，至于较为复杂的综合运用，将安排在接下来的教学活动中进一步达成．

教学问题诊断分析

七年级的学生在本章刚刚经历了数与式的承接，初步体会了用字母表示数的数学思想，即将进行分式运算的学习．此外学生在六年级学习分数运算时，已经有过类似的学习经历，为本节课的学习奠定了基础．

但是对于大多数学生而言，还不能自主地将两者联系并进行类比，因此在学完整式运算以后，对突然冒出来的“因式分解”不免心生疑惑：难道仅仅是整式乘法的逆过程吗？这样的代数变形意义何在？到底为什么要学习因式分解？基于以上分析，笔者认为对核心概念“因式分解”的理解是学生学习中遇到的难点．

教学支持条件分析

为了有效实现教学目标，笔者设计了如图1所示的板书，在教学过程中逐渐展开.

图1

板书能生动、有效地帮助学生由“数”及“式”地联想类比，使有关概念被有效地数学理解．在课件中，将“提取公因式法”所含各个字母或符号的“组件”，动态地进行时间与空间的二维组合，形象地展现“提取公因式法”公式的形成与确立．板书与课件随着学生的思维同步展开．

教学过程设计

1．类比旧知、揭示课题

在这个教学环节中，笔者开门见山地启发学生思考：接下来将要学习什么内容？

数学学习是具有连续性的，这种连续性很大程度上体现在数学学习过程中知识的联系与运用．学生在六年级经历了从整数运算到分数运算的过程，并在学习分数运算前认识了因数、公因数、分解素因数等，这些学生已有的知识与本课的有关概念能够自然联系，匹配类比（如图2），既自然地揭示本课内容，又能让学生对于为什么要学习因式分解有了明确的目标，脑海中埋下了应用的意识，也有助于对核心概念——因式分解的理解．

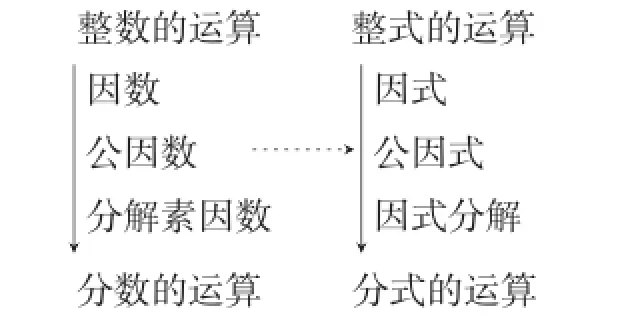
图2

2．由“数”及“式”，迁移知识

围绕问题“什么叫做因式、公因式、因式分解？”展开．

引导学生从具体的内容着手，自发地将“数”的分解的学习经验迁移到“式”的分解中，再尝试抽象归纳有关概念，让学生经历概念发生、发展和形成的过程，也在课堂上创造了用数学语言概括与表达的机会，并最终使整个概念系统得以完备．

在这两个教学环节中，笔者运用的教学策略是：类比联想，逐步形成有关概念，此时学生已经具备了完成引例的能力，进入第三个教学环节.

3．尝试运用，理解内涵

放手让学生尝试对多项式6xy2+9xy分解因式，通过“三问”驱动学生深入理解因式分解，再及时归纳出提取公因式的方法，并强调检验．

这里运用了教学策略2：问题驱动，深入理解核心概念．

要求对结果提出“三问”（也是今后因式分解的“铁律”）：

（1）结果中哪些是单项式因式？哪些是多项式因式？

（2）结果是否已经是几个单项式因式或多项式因式的积的形式？

（3）结果中每个多项式因式是否不能再分解因式了？

其中问题（1）、问题（2）着眼于对“因式”的真正理解；问题（3）着眼于对因式有类似素因数的“素”的要求的理解．用“三问”驱动反思，期盼学生对因式分解的概念真正的理解．

4．例题解析，了解规范

将因式、公因式这些概念融化在解题的过程中，继续在“三问”中内化核心概念因式分解，并且巩固提取公因式的方法．

数学语言的表达除了课堂上的口头交流外，也体现在解题时的书面表达，通过对例题进行解析与板演不仅是对本课两部分教学内容进行巩固运用，也是必要的书写格式的示范．

这里运用了教学策略3：注重规范，讲究数学语言表达．

5．巩固练习，提高能力

练习：分解因式：（1）15a2b+3ab；（2）a2n+an-1-an（n≥2，且n为整数）．

学生独立练习的过程也是对本课内容理解、内化的过程．

第（1）小题是基础练习，第（2）小题多项式次数为字母表示，在提取公因式时，需要对归纳方法中的“最低次幂”有准确的认识，方可正确找出公因式an-1，即使有些学生不能一步到位找对公因式，也可以通过对结果进行“三问”或进行概念辨析来修偏、纠正．期盼通过这两个练习，对本节课的目标达成度进行检测与评价．

6．梳理总结，承前启后

问题串：为什么没有专门研究单项式的因式分解呢？

本节课的教学内容既与六年级“数”的分解有着承前的功能，又对于接下来分式运算的学习有着启后的价值.学生通过自主小结和教师引导，体会数学学习是知识结构螺旋上升的过程．

全课以一个饶有回味的问题作为结尾，目的是加深学生对因式分解本质的理解．

参考文献：

［1］中华人民共和国教育部制定．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］胡华春.认知负荷理论对数学样例教学设计的启示［J］.中国数学教育（初中版），2012（4）：2－4，9.

［4］许芬英，胡赵云.从一节公开课的教学设计看如何活化与活用教材［J］.中国数学教育（初中版），2014（1/2）：3-6.

［5］张爱平.基于“四基”的初中数学课堂教学设计的思考：以苏科版课标教材七年级上册“有理数和代数式”为例［J］.中国数学教育（初中版），2013（3）：20-24，30.

收稿日期：2015—12—19

作者简介：沈艳秋（1984—），女，中学一级教师，主要从事初中数学教育教学研究．