冲突经济学视域下的阶级斗争与社会变革

■刘 涛

冲突经济学视域下的阶级斗争与社会变革

■刘 涛

马克思经济学理论中，生产力与生产关系的矛盾是社会变革的原因。利用冲突经济学中的CFS模型，采用阶级的分析方法，对上述论断提供一种证明。不同阶级掌握的生产力水平决定了本阶级资本存量的积累速度，资本存量决定了斗争的有效性。根据CFS，阶级斗争的过程大体可以分为四个阶段，各阶级根据斗争有效性采取不同的策略，各阶段随之呈现激烈与缓和斗争状态。掌握先进生产力的阶级取得胜利具有必然性。研究显示了阶级斗争也是有效率的资源配置方式。

生产力；阶级斗争；社会变革

一、导 言

对于社会变革甚至社会革命为什么会发生，经济制度为什么会发生更替，西方主流经济学难以给出满意的解释。原因主要包括以下两个方面：第一，研究内容存在不足。西方主流经济学欠缺冲突方面的研究，在其理论中，冲突被概念化为与交易、合作等相对应的理性行为人的某种行为。［1］这样冲突成了经济模型中的个别现象。然而现实中的冲突是普遍现象，各个冲突方的行为是复杂的，西方主流经济学的这一缺陷使其在很多具体问题上缺乏解释力。像资产阶级革命这

样时间久、过程反复、冲突剧烈的社会革命似乎已经超出了西方主流经济学的解释范围。为弥补西方主流经济学的不足，赫什利弗（1995）、加芬克尔和什卡佩尔达斯（2007）等建立了冲突经济学［2］，对社会冲突现象进行研究。赫什利弗认为冲突经济学应该是与微观经济学并行的两大分支。虽然目前关于冲突经济学的研究越来越多，然而西方主流经济学仍未将其纳入主要视野。除此之外，冲突经济学框架中关于冲突与经济发展的关系的研究也存在不足，比如现有的研究对冲突影响经济的正向作用涉及较少。尽管如此，冲突经济学的研究方法为研究社会冲突提供了很好的分析工具。第二，研究立场方面的原因。秉承自萨伊以来的传统，西方主流经济学不愿关注阶级斗争。为了建立“纯粹的”经济学，其理论对社会制度的假设是中性的，对各参与方的假设也多是无差异的，实际上就没有阶级的概念，更加不会存在阶级斗争。事实上，阶级与阶级斗争都是客观存在的，封建地主阶级和资产阶级的斗争是漫长而激烈的，矛盾是不可调和的，否则也不会发生所谓的资产阶级革命。因此，西方主流经济学超阶级的立场是罔顾现实的。

马克思对社会变革及社会革命有着深刻的认识，他从生产力与生产关系的内在矛盾，揭示了社会革命发生的必然性。马克思在《政治经济学批判》序言中写道：“社会的物质生产力发展到一定阶段，便同它们一直在其中运动的现存生产关系或财产关系（这只是生产关系的法律用语）发生矛盾。于是这些关系便由生产力的发展形式变成生产力的桎梏。那时社会革命的时代就到来了。随着经济基础的变更，全部庞大的上层建筑也或慢或快地发生变革。”［3］这不仅解释了历史上所有社会变革发生的内在机理，而且揭示了社会制度变迁的影响与趋势：掌握先进生产力的阶级，必然通过阶级斗争，挣脱旧有生产关系的束缚，掌握国家政权，建立与生产力水平相适应的新的生产关系。因此马克思和恩格斯说：“至今一切社会的历史都是阶级斗争的历史。”［4］在社会革命的过程中暴力冲突始终是不可避免的手段，但无论是否发生暴力冲突，先在经济上后在政治上取得统治权力是必然结果，而且这一改变使得经济发展处于更高水平。正如恩格斯在探讨资产阶级革命时所指出的：“（资产阶级）通过‘经济状况’的改变，而政治状态的改变则是或早或迟，或自愿或经过斗争随之发生的。资产阶级反对封建贵族的斗争…在这一斗争中，资产者的决定性武器是他们的经济上的权力手段…革命不是按照杜林先生的原则，使经济状况适应政治状况，而是相反，把陈腐的政治废物抛开，并造成新的‘经济状况’能够存在和发展的政治状态。”［5］

本文以马克思经济学为指导，利用冲突经济学的理论模型，采用阶级的分析方法，对阶级因经济权力的变化和社会变革的发生提供一种证明。首先介绍冲突经济学的核心模型斗争成功函数（CFS）以及该模型的静态和动态均衡，使用CFS探讨阶级间经济权力的变化、阶级斗争及阶级地位的变迁，然后使用演化模型描述了最终斗争失败阶级的消亡，并论证阶级斗争是有效率的资源配置方式，最后得出本文的结论。

二、CFS基本模型、静态均衡和动态均衡

西方主流经济学中，各经济主体的行为符合最优化原则，最终达到静态均衡。这些均衡明显和现实有较大差异，现实中非均衡和冲突是常态。冲突经济学通常使用斗争成功函数（Conflict Success Function，CSF）这一专门的模型用来描述冲突。该模型原本是国防经济学中用来分析国家间冲突以及国防投入对国家经济影响，但也被广泛的应用于分析各种争端行为。假定冲突来自对某项特定争议资源的分配，有两个参与者A和B，两个参与方之间的资源分配额度PA和PB取

决于CFS。有关于CFS的基本模型、静态均衡和动态均衡如下［6］：

基本模型：

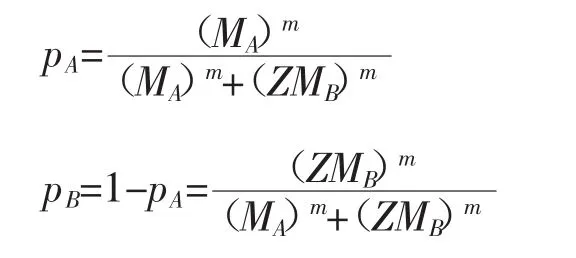
双方投入冲突的资源为MA和MB，m＞0为决定性系数，Z＞0为B投入资源的有效性水平。假定双方都没有投入冲突资源，即MA=MB=0时，pA= pB=0.5，就是说双方各得一半；当投入冲突资源不为0时，若Z=1表示双方投入冲突资源的有效性相等，Z＞1表示投入相同数量的冲突资源时，B的冲突资源更加有效率，Z＜1时相反。

（一）静态均衡

假定双方对特定的收益R进行分配，冲突时不会造成R的损失，为简单起见，假定m=1，阶级A的所得为：

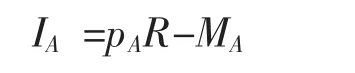
在《冲突经济学原理》一书中有该模型详细的数学推导过程，为了节省篇幅，本文省略了该过程，直接给出求该式最大化的结果：

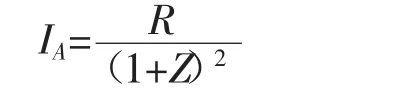
同样可以求出：

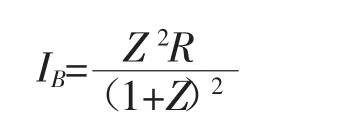
可以看出，双方收益和投入冲突资源的有效水平有关，这个指标表明双方力量对比，当Z=1时双方力量相当，此时各得联合收益的一半；当0＜Z＜1时，即A的力量要强于B，此时的分配对A有利；当Z＞1时，B的力量要强于A，此时对B有利。

（二）动态均衡

在模型中双方都要投入冲突资源，这些资源的目的就是为了争夺资源R，因此并不进入生产领域，也就是说不创造新的价值，而是在冲突中损耗掉了。但是对优势一方，这种损耗是有利可图的，为了说明这种情况，我们假定B是占优势一方，因此Z＞1。假定第一阶段B先做出选择是否投入冲突资源，第二阶段A看到B的行动之后做出选择是否投入冲突资源。则博弈树如图1。

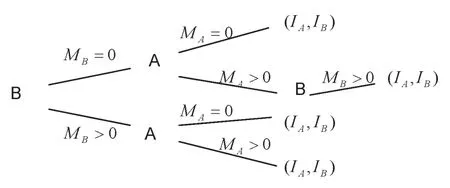
图1

首先来假定第一阶段B已经选择了MB=0，A选择MA=0，根据前面的设定，双方将各得0.5R；如果A选择MA＞0，则如果只有两阶段博弈的话，根据1式和2式，会有pA=1和pB=0。因此当B选择MB=0时，A一定会选择MA＞0，此时B的收益为0。但是现实中不会出现B的收益为0这种情况，因为如果A选择MA＞0，除非规定强行禁止B进行反击的规则，否则B必然会在下一阶段选择MB＞0。假定A选择了MA＞0，此时B的选择为最大化：

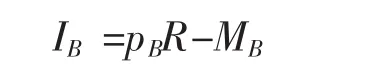
同样，我们省略推导过程直接给出结果：

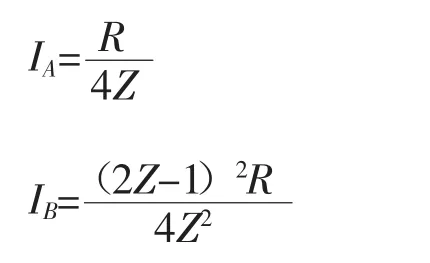
因为Z＞1，可知必然IA＜0.5R，因此当B选择MB=0时，A应当选择MA=0。

再假定第一阶段B选择MB＞0，第二阶段A的选择即为收益最大化问题：

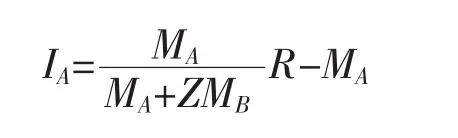
直接给出结果为：

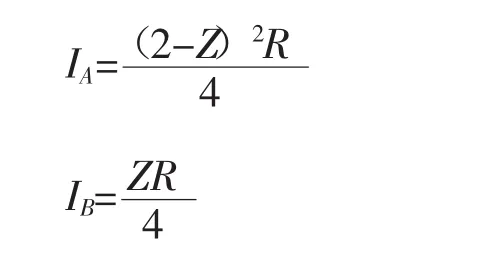
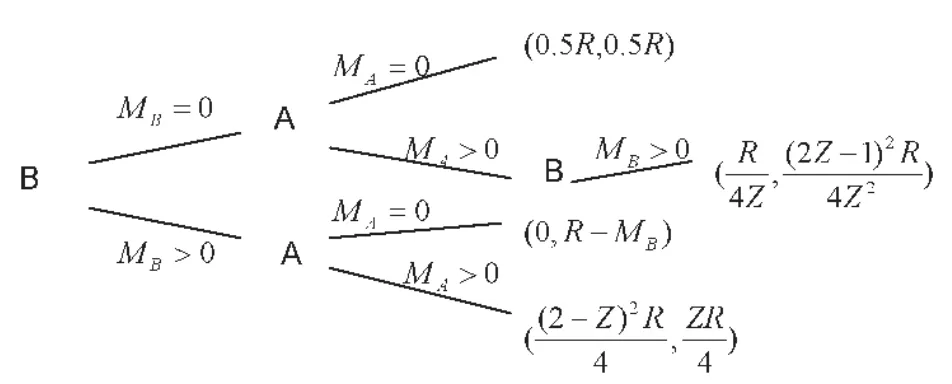
图2

当Z≥2时，IA≤0，而根据规则规定当MA=0时，IA=0，因此当Z≥2时，如果B选择MB＞0，A在任何时候都会选择MA=0，此时B将获得全部收益；由于假定Z＞1，因此当1＜Z＜2时，B选择MB＞0；当1＜Z＜2时，因此应当选择MB=0。

因此该博弈的均衡路径为（图2）：当Z≥2时，B选MB＞0，A选MA=0，均衡收益为（0，RMB）；当1＜Z＜2，B选择MB=0，A选择MA=0，均衡收益为（0.5R，0.5R）。

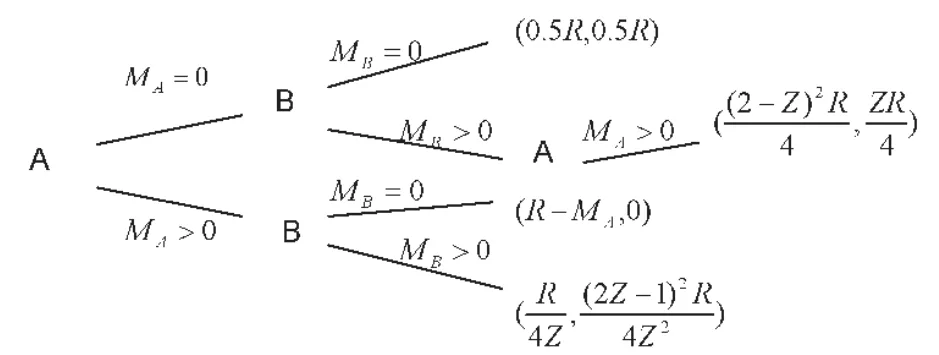
图3

如果由A首先做出选择，从图3可以很明显看出，如果Z≥2，唯一的均衡路径是：A选择MA＞ 0，B选择MB＞0，均衡收益为即斗争均衡，该均衡为内点均衡，因为如果此时A选择MA=0，B必然会选择MB＞0，而A不得不屈服；如果1＜Z＜2，那么A选择MA=0是合理的，因为如果B选择MB＞0，下阶段A还可以选择MA＞ 0，此时，双方所得都严格小于（0.5R，0.5R），因此在1＜Z＜2时，均衡路径为A选择MA=0，B选择MB=0，均衡收益为（0.5R，0.5R），该均衡是角点均衡。因此如果双方实力差距较大的时候（本文为Z≥2），先发和后发具有完全不同的结果，对于劣势一方来说，争取先发是有利的；而如果实力差距较小，不会发生冲突。

在双方实力差距较大时（本文为Z≥2），结果与先后行动的顺序有关。确切地说，冲突中先动的一方总有先发优势，无论是否是占优势的一方。当双方实力差距较小时，双方都会有所顾忌，通常发生冲突的概率较小，因为一旦冲突将使双方投入大量冲突资源，最终冲突的结果使双方的获益小于不冲突的获益。

以上即CFS的基本内容，可以看出，CFS为冲突的研究提供了一个有用的工具。但是，CFS在应用于具体问题的分析时需要注意一些问题：首先，CFS的参与方在本质上是同质的，其差别需要在假设条件时特别加以说明，尤其是对冲突资源的有效性如何界定。其次，在很长时期中，参与人的角色将发生转换，CFS的动态均衡要在变化中及时调整，结论才能有效。如现有的研究认为，冲突中所耗费的冲突资源在模型中是非效率的，阻碍了经济增长，［7］但是，马克思经济学明确指出阶级斗争促进了生产力的进步，如果将冲突资源的耗费与争夺资源的产出进行一个长时间的对比就会发现马克思经济学在这个问题上的先见之明。在后面的分析中，我们可以看到，当阶级的因素加入之后，整个模型都将相应发生变化。

三、阶级斗争与阶级地位的演化

恩格斯指出，历史上已发生的社会变革中，一个新的阶级之所以能够取代旧的阶级，关键的因素在于新的阶级掌握了更加有效的生产方式，

代表更高的生产力。

假定社会上只有阶级甲和阶级乙，阶级甲是旧阶级，阶级乙是新阶级，在初始阶段阶级甲是统治阶级，阶级乙是被统治阶级，双方以各自不同的方式进行生产。再假定两个阶级的生产效率存在差别，阶级乙的生产效率高于阶级甲，阶级乙是更高生产力的代表。阶级甲的产出用 y表示，阶级乙的产出用Y表示，如果生产分多期进行，则第t+1期的双方的产出分别为：

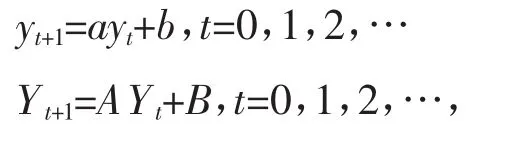
如果方程是自治的，且A＞at＞1，则：

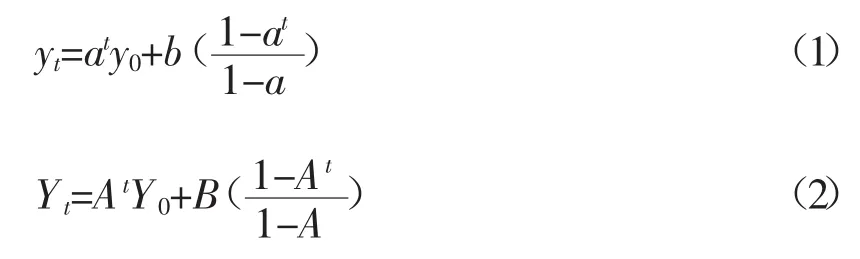
其中y0和Y0分别是两个阶级生产资本的初始状态。在初始阶段，阶级甲是统治阶级，生产资本的初始状态要远远超过阶级乙，即y0＞Y0。

现在我们考察阶级斗争过程的演进。假定待分配的社会资源总数为R，该资源由一不属于两个阶级的主体Ψ生产，假定每一期社会待分配资源分配完毕之后，两个阶级利用该资源进行生产，同时对Ψ进行补偿，在每一期生产结束时，Ψ利用补偿生产新一期的社会待分配资源。根据CFS，对待分配的社会资源总数R，阶级甲的分配额度为P甲，阶级乙的分配额度为P乙，则双方所得分别为：

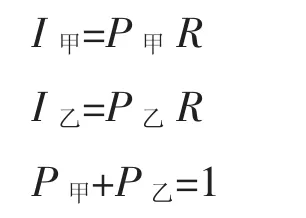
每一期生产完成之后，双方都要对新的社会待分配资源进行重新分配。对双方来说，分配额度的一个关键因素是投入冲突资源的有效性Z，这取决于双方产出的对比。为了方便起见，更加容易地使用CFS的动态均衡结论，我们假定投入冲突资源的有效性水平为双方资本存量比的单调增函数，即：

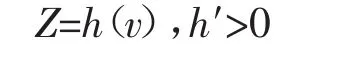
且：

1.h（1）=1

过程的演进分为如下几个阶段：

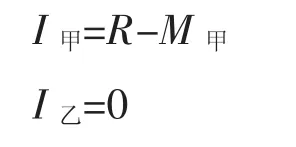
那么在第0期，两个阶级生产资本的初始状况为：

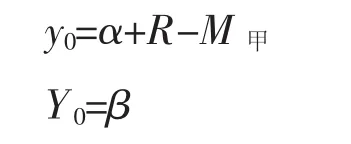
因为Y0＞α，则必然成立，其中M甲可以理解为阶级甲为了维护自身统治制定和运行的各项规则付出的成本，且假定这项成本在第0期付出后如果外部条件不发生变化就不需要再追加，直到重新分配社会资源时。阶级甲付出这项成本之后，阶级乙由于没有付出冲突成本，所以此时社会并没有冲突发生，两个阶级各自以初始的生产资本进行生产。

上述状况说明，当两个阶级实力相差很大的时候，作为统治阶级首先行动，只要付出较小代价就能够获得较大的利益，在资源争夺中占尽优

势。然而，这种先发优势并不总能保持，历史充满偶然性，均衡进程经常会被一些事件打破，比如统治阶级出现内乱，或者天灾、外敌入侵等等。一旦在随后某个时期出现这些事件，社会总资源可能面临重新分配，阶级乙将有机会首先进行选择，此时将出现一个新的初始状态。

若第k期阶级乙获得了重新选择的机会，根据CFS，即使此时期阶级甲的实力仍远高于阶级乙，阶级乙必然选择M乙＞0，阶级甲随后选择M甲＞0。此时，双方的初始生产资本已经发生变化，第k-1期结束时的产出即为第k期开始时双方的生产资本存量，阶级甲为ak，阶级乙为βk，则ak=yk-1，βk=Yk-1，此时仍然ak＞βk，且根据图3，此时对社会总资源Rk进行分配，状况为：

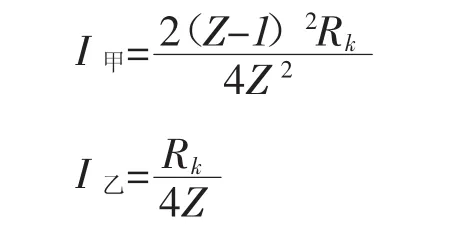
从第k期开始，两个阶级的生产资本的初始状况已经发生了变化：

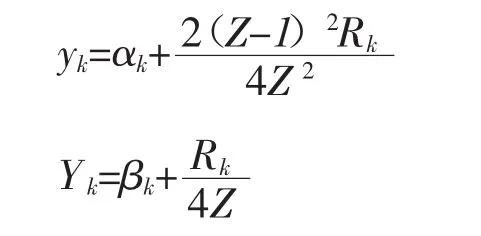
可以看出，此时阶级乙的分配状况要好于状况一时的状态。在这一过程中，阶级乙和阶级甲的冲突成本均大于0，社会爆发冲突。但是这种冲突对阶级乙来说是有利的，相比不冲突的一无所得，阶级乙已经能够从社会总资源中获得部分份额。因此，在双方实力相差较大的时候，处于弱势的阶级必然会寻找机会，通过制造冲突改变在资源分配中的格局，为自己谋取利益。弱势的阶级通过这种冲突获取的利益在优势阶级看来也许微不足道，但是这种冲突所具有的意义却是重大的。首先，这种冲突的发生具有必然性。只要统治阶级的统治出现缝隙，给被统治阶级先发的机会，被统治阶级一定会采取先发冲突的策略，这就证明了在阶级社会中，阶级斗争是必然发生的。其次，这种冲突是历史进程加快的原因。事实上，形如（1）式和（2）式的函数在其常数都大于0且u＞1时，导函数大于0，所以该函数是单调递增函数，此时若A＞ a＞1，则x取任意正整数值t时，有成立，也就是说，在其他条件不变的情况下，必有未来的某个时期j，使Yj=yj成立。因此，即使没有发生冲突，在没有外界干扰的情况下，由于在生产效率方面的优势，阶级乙也会在未来成为经济上占优势的阶级，问题在于尽管最终结果不会改变，但这一过程可能发生的非常漫长。然而通过阶级斗争，阶级乙提高了在资源争夺中的份额，从而使这一过程加快。

由于阶级乙在生产效率方面的优势，在经过多期的生产，两个阶级在实力差距上逐渐缩小，过程将进入下一个阶段。

第二阶段，阶级甲实力超过阶级乙，但差距已经缩小。两个阶级的生产状况来看，存在一个生产时期的区间m＜t＜n，在此区间内，且1＜Z＜2。假定第l-1期在此区间内，该期结束后对社会总资源Rl进行重新分配。从第l期开始阶级甲已经拥有的生产资本状况存量为αl，阶级乙为βl，则αl=yl-1，βl=Yl-1，此时仍然αl＞βl，根据CFS，此时无论阶级甲还是阶级乙首先做出选择，双方都不会支付冲突成本，相应会选择和平策略，即M甲=M乙=0，此时双方在社会总资源分配中的份额分别为：I甲=I乙=0.5Rl。此时两个阶级将又在一个新的初始时期进行生产，拥有的初始生产资本状况为：

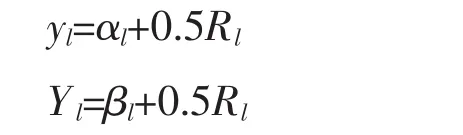
第l期成为新的初始时期，可以看到阶级乙的分配状况进一步改善，获得的社会总资源的份额进一步增加。随着生产时期的进一步增加，阶级乙的实力终将超过阶级甲，此时将进入第三阶段。

第三阶段，阶级乙的实力超过阶级甲，但差距不大。经过一段时期的生产，由于阶级乙的生产效率高于阶级甲，阶级乙的实力终于超过阶级甲。假定存在一个生产时期的区间p＜t＜q，在此区间内根据设定，但1＜Z＜2。此设定的目的是为了更简单的应用图2和图3的结论，并不影响CFS的结果。假定第s-1期在此区间内，该期结束后对社会总资源Rs进行重新分配。从第s期开始甲已经拥有的生产资本存量状况为αs，阶级乙为βs，则αs=ys-1，βs=ys-1，但此时αs＜βs。由于双方实力相差不大，与第二阶段一样，此时无论阶级甲还是阶级乙首先做出选择，双方都会选择和平策略，不会支付冲突成本，即M甲=M乙=0，此时双方在社会总资源分配中的份额分别为：I甲=I乙=0.5Rs。此时两个阶级新的初始生产资本又发生变化，状况为：

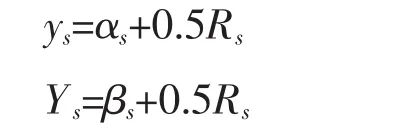
第s期成为新的初始时期。可以看到阶级乙的资源分配状况虽然没有变化，但是其产出已经超过阶级甲，从经济上来说，阶级乙已经成为优势阶级。经过一段时期之后，将进入第四阶段。

第四阶段，阶级乙的实力远超阶级甲。此时存在一个时期T*，当t＞T*时，此时v=，但Z≥2。假定第T-1期是超过第T*期的某个时期，该期结束后重新分配社会总资源RT，从第T期开始甲已经拥有的生产资本存量状况为αT，阶级乙为βT，则αT=yT-1，βT=YT-1，αT＜βT。由于双方实力相差很大，根据图2，可知如果阶级乙首先选择，则阶级乙必然选择M乙＞0，阶级甲随后选择M甲=0，双方的所得分别为：

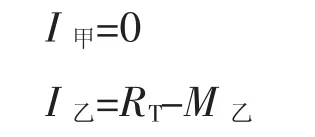
第T期开始的初始生产资本状况为：

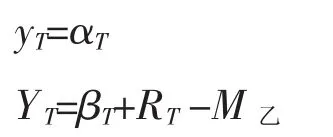
可知此时由于阶级乙处于绝对优势，只需要付出很少的冲突成本就可以占有全部社会资源，而阶级甲不会采取冲突策略。

若第T期阶级甲首先选择，根据图3可知阶级甲必然选择M甲＞0，随后阶级乙选择M乙＞0，此时双方所得分别为：

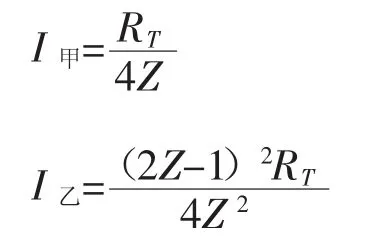
此时：

第T期开始的初始生产资本状况为：

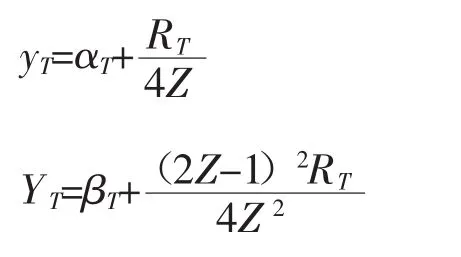
但是，根据（1）式和（2）式可知，随着时间的推移，Z的值会越来越大，R/4Z→0，阶级甲的冲突选择逐渐变得没有意义。阶级乙将获取全部社会资源，而且必将成为新的统治阶级。

四、旧阶级的消亡

上述分析描述了一个具有先进生产力的阶级如何在经济上取代另外一个阶级成为新的统治阶级。事实上到目前为止，斗争的结果是胜利的阶级完全掌握了社会资源的分配，但在已经发生的历史事实来看，阶级斗争中失利的阶级都已

经消亡，消失在历史长河中。演化经济理论为这个结果提供了一个解释：阶级成员并非一成不变，高效率的生产方式会被不断模仿，采用低生产效率生产方式阶级的成员会模仿新的高效率生产方式，在这个过程中，其自身的性质也相应地发生变化，一些阶级的成员由于生产方式的变化从而转化成另外一个阶级的成员，导致原有阶级的成员数量将逐渐减少，最终该阶级完全消失，整个社会关系也彻底发生变化。这应当是导致阶级消亡的重要原因。本文之所以采用演化理论分析这一问题，是因为作者认为一个阶级的消亡并非是由于在某个时点该阶级成员被另外一个阶级集体消灭，而是经过一个演化过程，阶级成员身份发生了转变。这在真实发生的历史上是得到印证的，如资产阶级形成过程中，相当一部分成员出身于封建贵族。

假定阶级甲的成员是随机配对交往，从开始都采取同一种方式生产。经过一段时间，在某一期有比例为X的阶级甲成员开始模仿阶级乙的生产方式。阶级甲生产方式的单位产出为y，阶级乙生产方式的单位产出为Y，则：

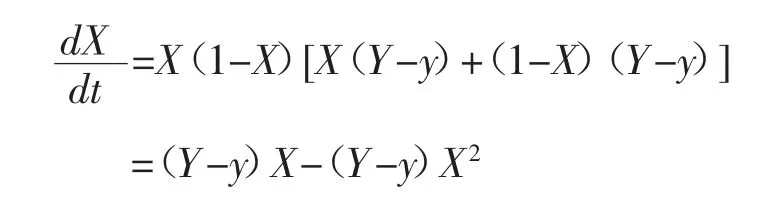
X=0和X=1

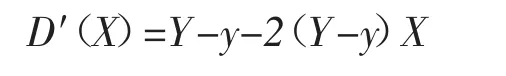
可知：

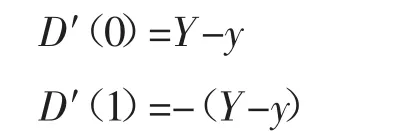
可知阶级甲的进化稳定策略（ESS）取决于Y-y的值，若Y-y＞0，X=1是ESS；若Y-y＜0，X=0 是ESS。因此，根据前文的假设条件，阶级乙采取的生产方式的效率要高于阶级甲，即Y-y＞0，因此X=1是ESS。这一结果显示在演化的过程中，阶级甲的成员将全部模仿阶级乙的生产方式，从而成为阶级乙的成员，阶级甲将最终消亡。

事实上，无论有没有斗争，上述模型的结果都会最终收敛到ESS。但是正如我们前面所说，斗争绝非没有意义，正是由于斗争的存在，加速了这一进程，使得掌握先进生产力的阶级能够快速取代旧阶级，并使得旧阶级消亡的进程缩短。

假定上述演化过程，阶级甲在没有冲突的条件下需要在第η期才能从第0期收敛的ESS。而第μ期开始，阶级乙通过阶级斗争取得统治地位，并在第θ期整个社会全部采取新的生产方式，η＞θ+1。这样从社会总产出的角度来看，在没有冲突的条件下，社会总产出为从第μ期到第η期的总产出为在存在阶级冲突的情况下，只要第μ期到第θ期两个阶级的总产出之和减去双方投入的冲突资源总量再加上第θ+1期到第η期的社会总产出大于没有冲突的社会总产出，即下列不等式成立：

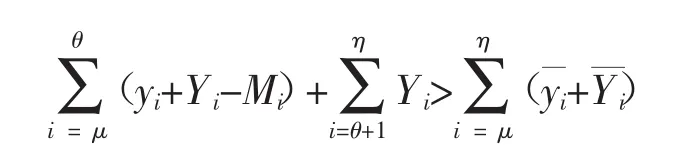
则阶级斗争就是有效率的。因此，相比没有斗争的演化过程，斗争使得资源能够更快的得到有效率分配。而且，增加的产出数量可能远远超过在阶级斗争中消耗的资源数量，资产阶级革命就是这样一种革命，正如《共产党宣言》中所说的那样“资产阶级在它不到一百年的阶级统治中所创造的生产力，比过去一切时代创造的全部生产力还要多，还要大。”［8］

五、结 论

本文使用冲突经济学的模型对阶级斗争与演化的过程进行了分析，为生产力与生产关系的研究提供了一种思路。通过研究证明，在并不严

格的假设条件下，掌握先进生产力的阶级通过阶级斗争建立与生产力发展相适应的生产关系是必然的，该阶级在资源争夺中投入的冲突成本促使了社会资源更快地被使用到更有效率的生产方式中去，因此阶级斗争也是有效率的资源配置方式。

［1］张旭昆，朱诚.收入分配、产权保护与社会冲突［J］.浙江大学学报（人文社科版），2014（1）：197-207.

［2］赫什利弗.冲突的理论［M］//哈特利，桑德勒.国防经济学手册：第1卷.姜鲁明，罗永光，译.北京：经济科学出版社，2001：164-189.

［3］马克思.政治经济学批判［M］//马克思恩格斯文集：第2卷.北京：人民出版社，2009：591-592.

［4］马克思，恩格斯.共产党宣言［M］//马克思恩格斯文集：第2卷.北京：人民出版社，2009：31.

［5］恩格斯.反杜林论［M］//马克思恩格斯文集：第9卷.北京：人民出版社，2009：171-172.

［6］安德顿，卡特.冲突经济学原理［M］.郝朝艳，陈波，译.北京：经济科学出版社，2010：229-230.

［7］刘涛雄.社会冲突与经济增长［M］.北京：清华大学出版社，2008.

［8］马克思，恩格斯.共产党宣言［M］.//马克思恩格斯文集：第2卷.北京：人民出版社，2009：36.

［责任编辑：丁浩芮］

Class Struggle and Social Transformation under the Perspective of Conflict Economics

Liu Tao

M arx's econom ics theory holds that the contradiction betw een productive forces and production relations is the cause of the social revolution. The above conclusion can be proved by using C FS M odel and the analysis m ethod of the class in this paper. Productivity level of each class determ ines the speed of the accum ulation of capital stock. The accum ulation of capital stock determ ines the struggle efficiency of the class. A ccording to the C FS， the process of class struggle can be divided into four stages. E ach class takes special strategy according to struggle efficiency in different process.Then the process show s violent or calm status. The class w hich m asters the advanced productivity w ill w in the struggle in the end. R esearch show s the class struggle is the efficient w ay of resource allocation.

Productivity； C lass Struggle； Social Transform ation

F014

A

1673-8616（2016）04-0039-09

2016-01-18

刘涛，中共贵州省委党校发展研究院副教授（贵州贵阳，550028）。