应用模糊数学方法评价河池市大气环境质量

李文玉（547000）



应用模糊数学方法评价河池市大气环境质量

李文玉（547000）

随着经济的迅速发展，城市大气环境质量问题愈来愈受到人们的重视.由于大气质量的综合评价存在着一定的模糊性，因此大气环境质量评价可以引用模糊评价法。模糊综合评价通过选用SO2，NO2和PM10作为评价因子，对照《环境空气质量标准》（GB3095-1996），经过适当的权重计算，建立评价矩阵进行综合评价。本文主要以河池市2012～2014大气监测数据为例，模糊评价结果表明：河池市大气污染主要是可吸入颗粒物PM10，2012～2013总体大气环境质量为Ⅰ级（清洁），但是2014年大气环境质量处于Ⅰ级和Ⅱ级之间，大气质量有所下降。本文为河池市大气防治工作提供一定参考。

大气质量；河池市；模糊综合评价；隶属度

1　引言

我国随着经济高速发展，城市化进程突飞猛进，大气污染对环境和城市居民的健康影响日益突出，引起了普遍关注。大气质量影响因素主要包括工业生产、居民生活、交通运输和垃圾焚烧等。由于大气环境系统自身就是一个多因素互相作用的复杂系统，而污染的空气成分一般又较为复杂。目前国内评价空气质量一般采用大气质量指数法，但是该方法忽略了不同浓度间的统计性差异，不能客观反映实际空气质量状况，而模糊理论正是将模糊不确定的因素量化，从而进行综合评价［1～2］。河池市隶属于广西壮族自治区，地处广西西北边陲、云贵高原南麓，是大西南通向沿海港口的重要通道，是广西实施西部大开发的重点区域。为了使评价结果更加客观的反映当地空气污染及其变化规律，进而制订相应有效的防治对策，本文应用模糊数学原理，通过计算各污染水平的隶属度，对2012～2014河池市环境空气质量进行综合评价。

2　模糊综合评价模型［3～6］

模糊数学是用数学的方法解决模糊的问题。

2.1建立因子集

根据相关国家环境标准规定，确定相关环境质量的因素即为因子集。建立因素集U=｛u1，u2，…，un｝，即有n个评价指标。

2.2建立评价集

根据国家标准取V为分级集合即为评价集。v=｛v1v2，…vm｝，即代表评价等级、分类的集合每一等级可对应一个模糊子集。

2.3建立隶属函数。

2.4单因子模糊评价

根据隶属函数，可确定各指标实际值的隶属度，进行单因素评价，并得到隶属度模糊关系矩阵

2.5建立权重集［7］

单项指标在总体权重的大小与某种用途的单项分级标准无关。所以对权重用公式Pi=Ci/Si，为了进行模糊运算，各单项权重还须归一化，得Wi=PiΣPi，对于模糊集合U上的单项指标的权重，写成矩阵，即得权重模糊矩阵。

2.6模糊综合评价过程

3　模糊评价实例（如表1）

模糊综合方法具体参考本文第二部分。

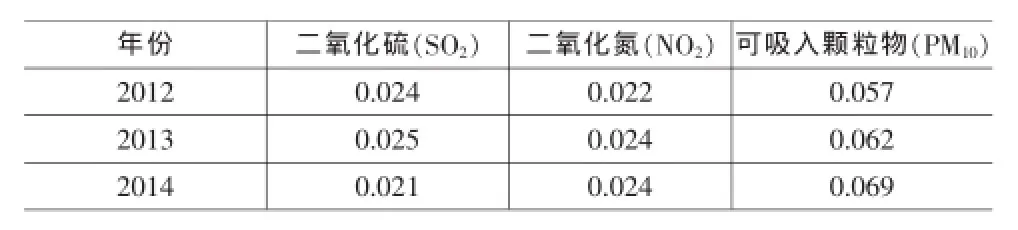
表1　2012～2014河池市大气污染物监测数据（单位：mg/m3）

在进行空气污染评价时首先取U为各因子指标集合，即取：U=｛1，2，3｝，其中U1表示SO2二氧化硫，U2表示NO2二氧化氮；U3表示可吸入颗粒物PM10。根据国家空气质量标准［4］和国内一些城市大气实际污染水平把空气质量分为四个级别，取V为空气质量分级集合，评价集V=｛Ⅰ，Ⅱ，Ⅲ，Ⅳ｝。

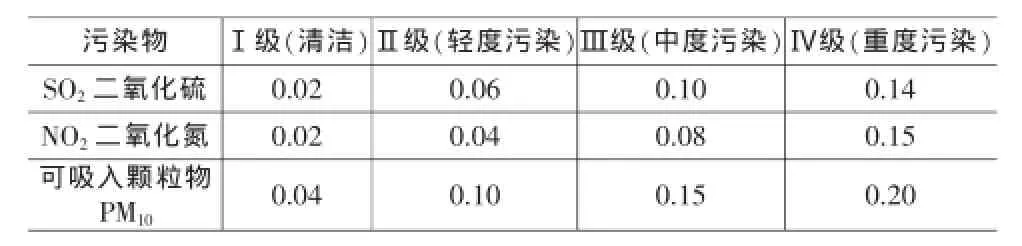
表2　环境空气质量分级标准（单位：mg/m3）

根据取最大隶属度原则，2012年和2013年河池市空气质量属于Ⅰ级，清洁。但是2014年河池市空气质量对于Ⅰ级标准的隶属度为49%，对Ⅱ级空气标准的隶属度为48%，两者十分接近，故可说明2014年河池市的空气质量有所下降。另从各评价因子权重系数结果可知，2012～2014年河池市主要空气污染物为可吸入颗粒物PM10。

4　结论

由于大气环境系统是多因素的耦合，评价大气环境的好坏过程中存在着相当的不确定性，等级的划分界限也很模糊，因此模糊综合评价方法是一种较为理想的评价工具。用模糊理论中的隶属函度来界定空气环境质量的分级边界，考虑了界限的模糊性，较客观的反映了评价结果。

［1］陆玉书.环境影响评价［M］.北京：高等教育出版社，2001.

［2］刘普寅，吴孟达.模糊理论及其应用［M］.长沙：国防科技大学，1998.

［3］杨绪勤.模糊数学在大气环境质量评价中的应用［J］.上海环境科学，1989（1）：14～17.

［4］《环境空气质量标准》（GB3095-1996）.环境科学出版社，1996：1～2.

［5］梁保松，曹殿立.模糊数学及其应用［M］.北京：科学出版社，2007．

［6］YIN Y Y，HUANG GH，HIPEL KW.Fuzzy relation analysis formulticriteria water resources management［J］.Journal of Water Resources Planning and Management，1999，125（1）：41～47．

［7］Chu A T W，Kalaba R E，Spingam K.A comparision of two methods for determining the weights of beinging to fuzzy sets［J］.Journal of Optimization Theory and Application，1979，7（27）：531～538．

2016-3-11

X823

A

2095-2066（2016）09-0220-01