苏嵯输油管道混合原油凝点计算方法

王倩楠，张海涛，司马英杰， 王佳楠，董良辰，周 刚

（1. 东北石油大学 石油工程学院， 黑龙江 大庆 163318；　2. 大庆油田有限责任公司储运销售分公司，黑龙江 大庆 163318；3. 大庆油田有限责任公司天然气分公司， 黑龙江 大庆 163318）



苏嵯输油管道混合原油凝点计算方法

王倩楠1，张海涛2，司马英杰3， 王佳楠1，董良辰1，周 刚1

（1. 东北石油大学 石油工程学院， 黑龙江 大庆 163318；2. 大庆油田有限责任公司储运销售分公司，黑龙江 大庆 163318；3. 大庆油田有限责任公司天然气分公司， 黑龙江 大庆 163318）

对呼伦贝尔与塔木察格原油不同混合比例下进行凝点测试实验，并根据已有的混合原油凝点模型进行计算，优选了凝点计算模型。通过分析实验数据，采用曲线拟合和最小二乘法进行模型修正两种方法得出苏嵯输油管道混合原油凝点计算公式，并对修正后模型和拟合出的曲线进行验证。实验数据表明修正后的模型较曲线拟合公式对于计算混合原油凝点结果更精准，可使原油的凝点较已有模型计算值的最小平均绝对偏差减小75%，较最大平均绝对偏差减小99%，较最小标准偏差减小45.77%，较最大标准偏差减小75.26%。

苏嵯；混合原油；凝点计算；数学模型

苏嵯输油管道主要承担着输送呼伦贝尔油田原油的任务，管道的设计输量为50～85万t/a，由于呼伦贝尔油田的开采量逐年降低，苏嵯管道的输油量达不到设计输量，同时，因为塔木察格油田原油外运仅有一条南线，年通关能力25余万t，难以满足油田生产需要，因此，将塔木察格原油运送至海拉尔油田苏嵯管道苏一联合站卸油点，由此苏嵯管道承担着输送塔木察格原油和呼伦贝尔原油的重大任务。由于塔木察格原油凝点高，流动性差，两种原油混合后的凝点难以确定，给原油的管输及储存作业造成了许多困难。因此，对两种原油混合后的凝点进行实验，并通过分析实验数据得到关于苏嵯输油管道混合原油凝点的计算公式，更方便现场实际应用。

1　实验条件

本实验的凝点测试是按照我国石油行业标准SY/T0541《原油凝点测定法》进行的，测试的油样均通过物理加热脱水处理，不含水，实验结果准确。本实验采取的实验方法是将原油经过恒温水浴预热至（50±1）℃，装入试管中，以0.5～1 ℃/min的冷却速度将油样冷却至高于预期凝点8 ℃时，每降1～2 ℃观测一次油样的流动性，直至将试管水平放置油样不流动时的最高温度即为所测凝点。

2　混合原油的凝点模型

通过查阅大量的文献资料发现关于混合原油凝点的计算模型较多，共有线性模型、李闯文模型［1，2］、陈俊经验公式［3-5］、刘天佑I模型［6］、刘天佑II模型［7，8］，将已有的几种关于混合原油凝点预测模型的计算值与混合原油凝点的实测值进行对比（见表1表2），综合考虑平均偏差、平均绝对偏差、标准偏差和最大偏差，优选出针对苏嵯输油管道混合原油凝点计算模型（见表3）。由计算结果可以看出，对于苏嵯输油管道混合原油的凝点计算，李闯文模型和刘天佑II模型偏差都较小。

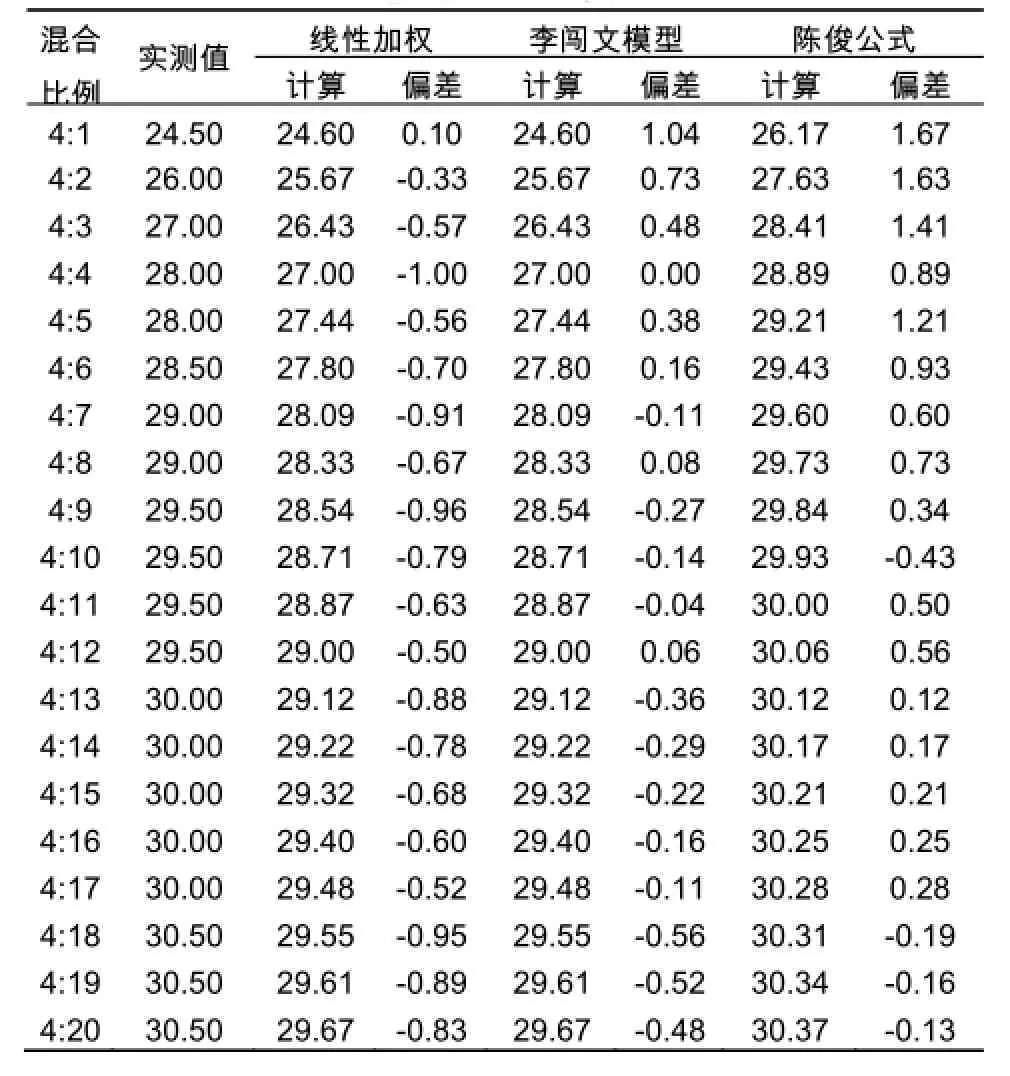
表1　呼伦贝尔原油和塔木察格原油按不同比例混合后凝点的计算值和实测值（一）Table 1 The calculated values and measured values of Hulun Buir and Tamtsag mixed crude oil in different proportions（1）

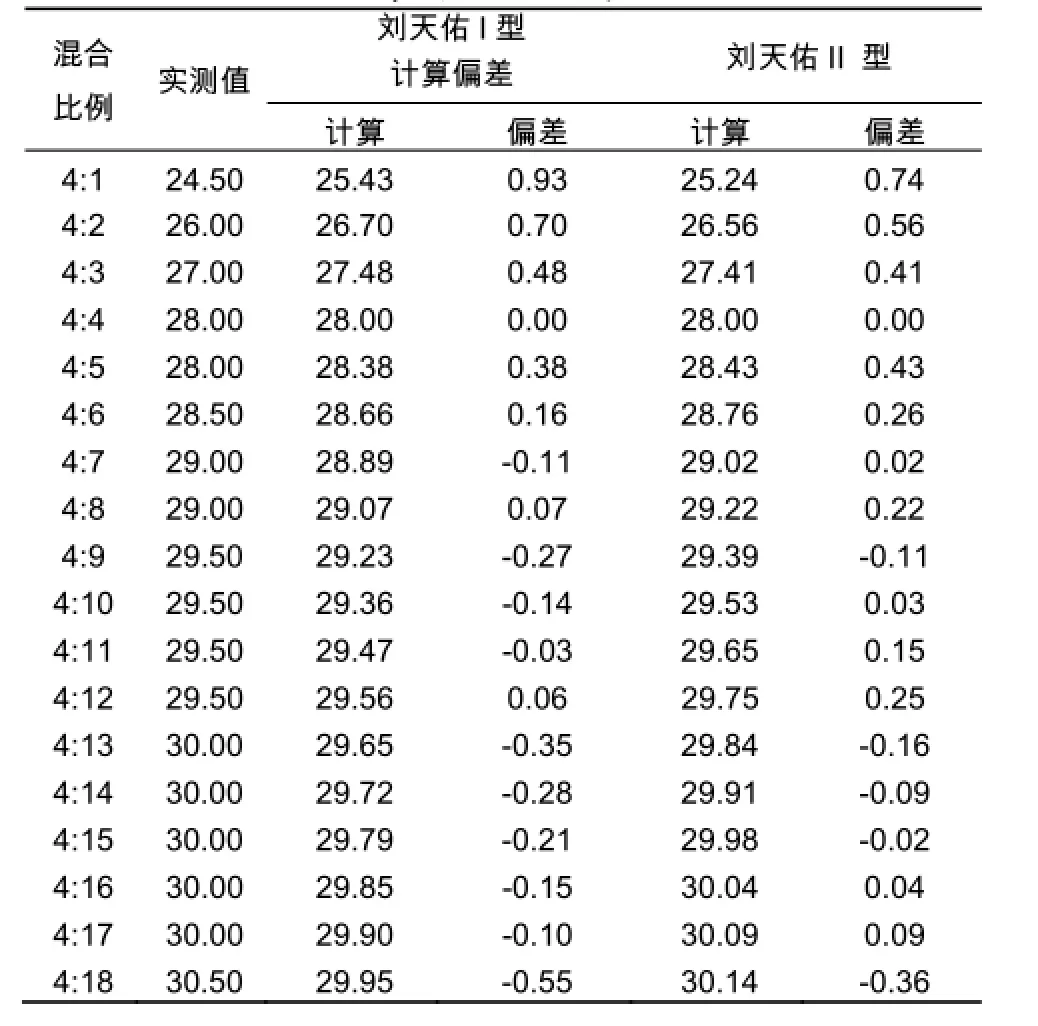
表2　呼伦贝尔原油和塔木察格原油按不同比例混合后凝点的计算值和实测值（二）Table 2 The calculated values and measured values of Hulun Buir and Tamtsag mixed crude oil in different proportions（2）

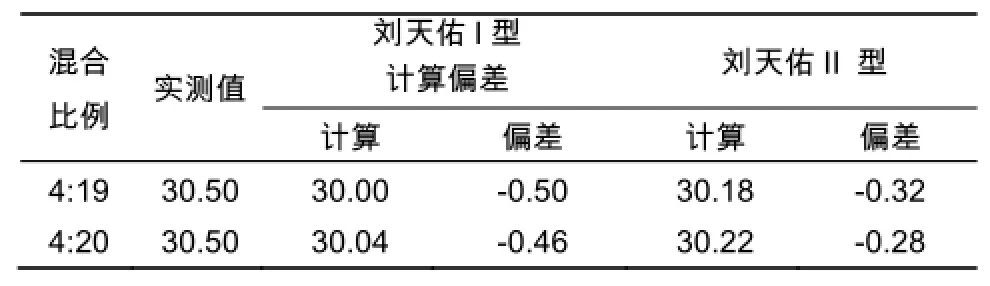
续表

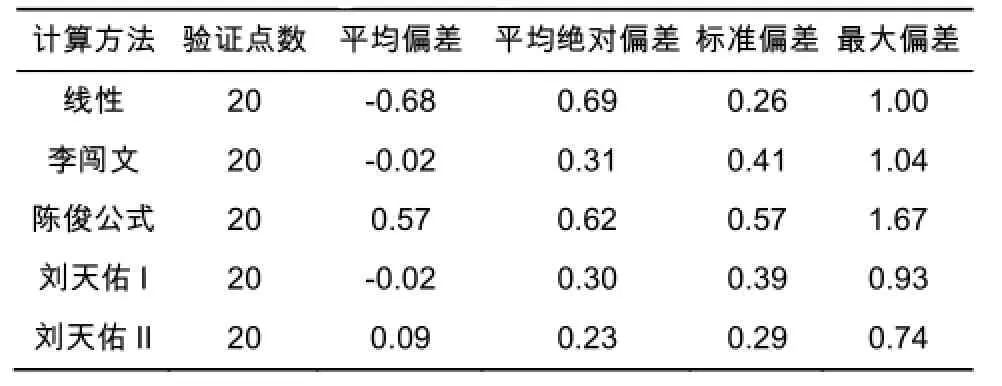
表3　凝点计算模型误差Table 3 Pour point computational model error

3　苏嵯管道混油凝点曲线拟合及模型修正

3.1曲线拟合

根据已有的凝点计算模型和修正模型，发现李闯文和刘天佑模型都必须需要两种组分原油1：1混合后的凝点值，计算起来有一定的局限性，而线性模型和陈俊的经验公式的误差相对于其他的模型会偏大。因此，考虑拟合出一个回归式只需要两种原油的混合比例便可以计算混合原油的凝点，而不需要两种组分原油1：1混合后的凝点值。由此，分析实验数据，发现混合原油凝点的实测值和高凝点原油掺入的比例有良好的相关性，由此进行拟合，得到的回归式为：y=-4.0676x2+13.486x+21.98，其中，y代表混合原油的凝点，x代表高凝点原油的掺混比例，见图1。

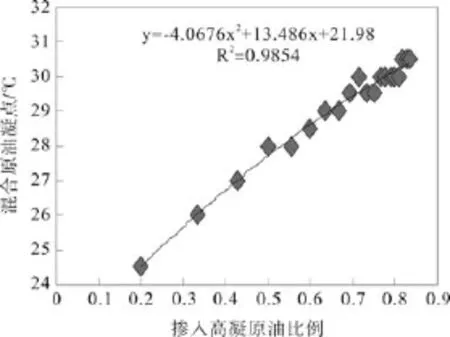
图1　塔木察格原油掺入比例与混油凝点的关系曲线Fig.1 The relation curve of Tamtsag oil mixing proportion and crude oil pour point

3.2模型修正

通过实验数据分析出李闯文模型和刘天佑II模型计算结果较准确，由此为提高混合原油凝点的计算精确度，得到苏嵯输油管道混合原油凝点的计算公式，对计算结果较好的模型进行修正。通过实验数据作散点图可以看出，混合原油比例和混合原油凝点的关系是非线性回归模型。非线性回归模型一般记为

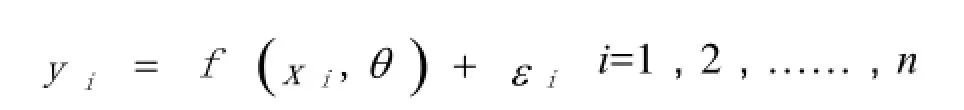
其中，yi为因变量；非随机向量xi=(xi1，xi2，……xik)是自变量；θ=(θ0，θ1，……，θp)为未知参数向量；εi为随机误差项并且满足独立同分布假定。

对于非线性回归模型，使用最小二乘法估计参数θ，求使得

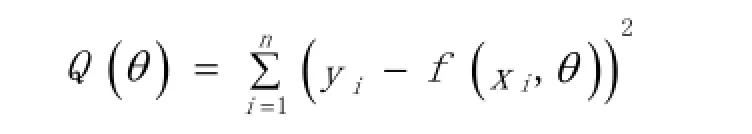
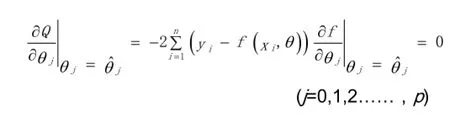
利用如上的非线性回归求解方法，分析实验数据，对混合原油凝点模型进行回归和参数求解，并通过整合修正已有的几种模型，得到苏嵯输油管道不同比例混输原油的凝点计算模型。

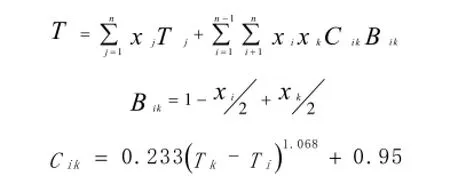
式中，T为混合原油凝点，xi，xk分别为第i，k两种组分原油中低凝点、高凝点组分原油的质量分数，Ti，Tk分别为低凝点原油和高凝点原油的凝点。

曲线拟合和模型修正二种方法的计算值与实测值的误差见表4。

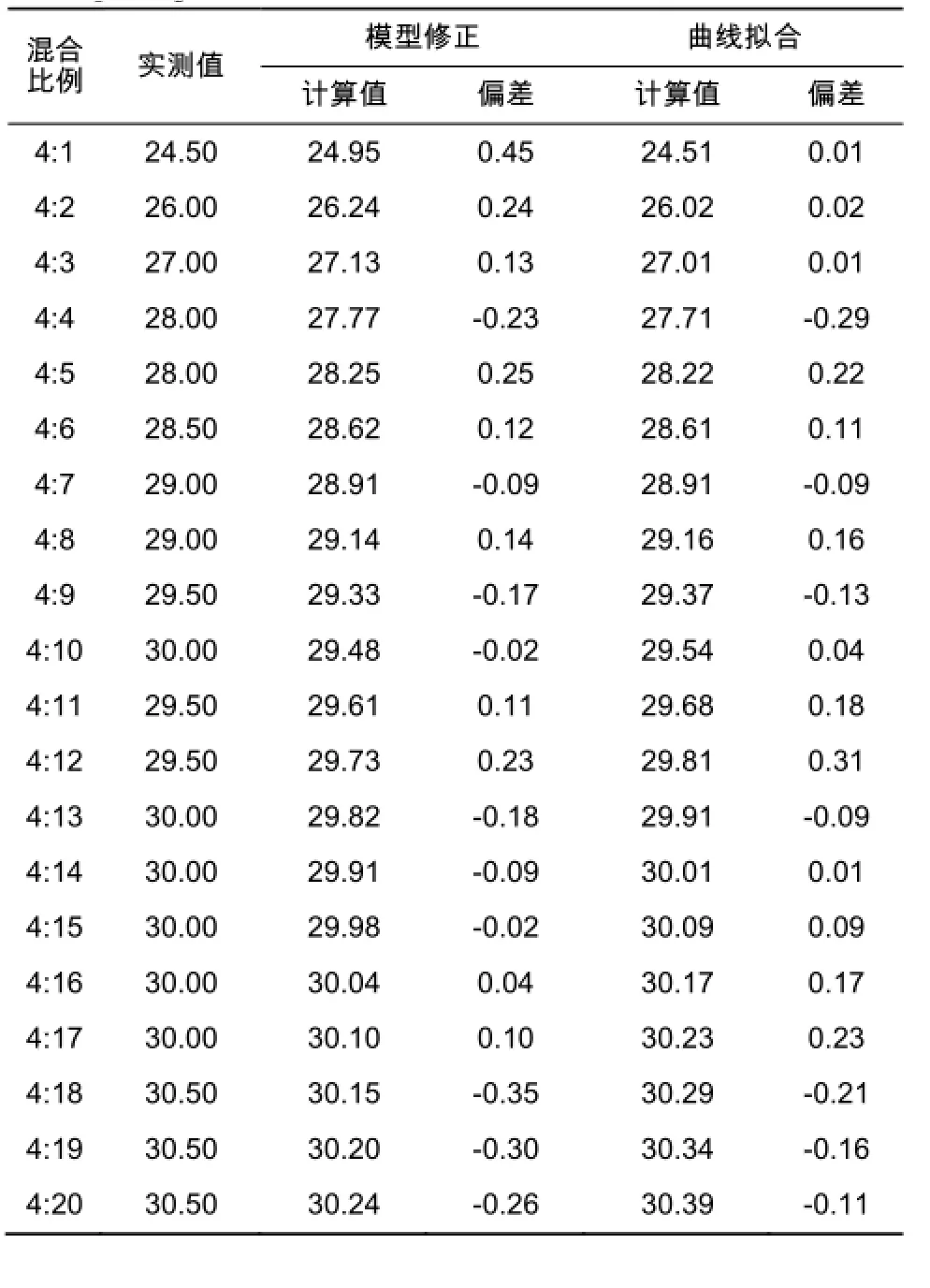
表4　呼伦贝尔原油和塔木察格原油混合后凝点的计算值和实测值对比Table 4 Comparison of calculated and measured values of pour point of Hulun Buir and Tamtsag mixed oil

运用同样的偏差计算方法来计算针对于苏嵯输油管道混合原油凝点模型的偏差。经过分析，曲线拟合的最大偏差为 0.310，平均偏差为 0.025，平均绝对偏差为 0.132，标准偏差为 0.160，模型修正的最大偏差为0.450，平均偏差为0.005 ，平均绝对偏差为 0.176，标准偏差为 0.141。由数据可以看出，两种计算方法对苏嵯输油管道混合原油凝点的计算结果较已有的模型更加准确，与已有计算模型相比，曲线拟合较最大平均偏差减小96.32%，较最小平均绝对偏差减小 42.61%，较最大平均绝对偏差减小 80.87%，较最小标准偏差减小38.46%，较最大标准偏差减小71.92%。模型修正较最小平均偏差减小 75%，较最大平均偏差减小99%，较最小平均绝对偏差减小 23.47%，较最大平均绝对偏差减小 74.49%，较最小标准偏差减小45.77%，较最大标准偏差减小75.26%。为使所得的经验公式具有普适性，排除实验数据的偶然性，因此对两种公式进行验证。

4　验 证

为了使回归的经验公式更加准确的用于计算苏嵯输油管道不同混合比例原油的凝点，排除由于实验比例相近而拟合出的曲线的片面性，在相同的实验条件和实验方法下，测量呼伦贝尔原油和塔木察格原油按照10：1，9：1，……，2：1等9组混合比例下的混合原油凝点，验证两种方法的准确性，使经验公式更方便的应用于现场。两种模型计算结果如表5，见图2。

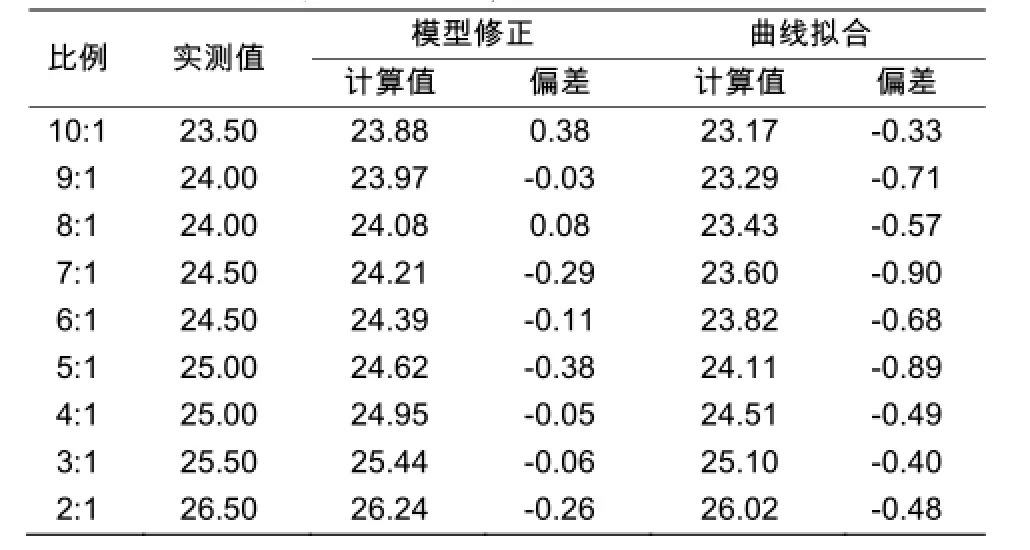
表5　验证模型准确性计算结果Table 5 Verifying the accuracy of the model calculation results

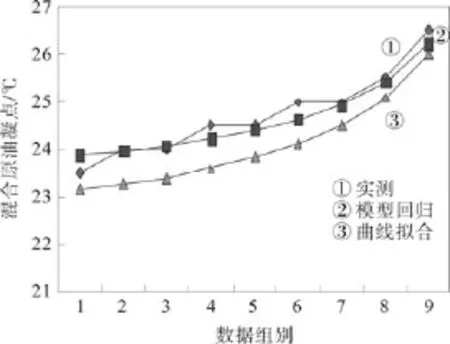
图2　验证模型准确性计算结果Fig.2 Verifying the accuracy of the model calculation results

（1）通过实验数据对已有的凝点计算模型进行分析、优选，得出李闯文模型和刘天佑II模型对于苏嵯输油管道混合原油凝点的计算偏差较小。

（2）对实验数据进行分析，得出两种针对苏嵯输油管道混合原油凝点计算公式，用9组数据进行验证，结果表明模型修正的误差更小，计算结果更准确。

（3）新方法对混合原油凝点的计算结果较现有模型的计算结果的准确性高，平均偏差减小99%，平均绝对偏差减小 74.49%，最大标准偏差减小75.26%。

［1］ 李闯文.混合原油流变学及其配伍规律的研究［D］. 北京：石油大学石油天然气工程学院，1992.

［2］ 贺常兵，张敬业，周靖林.现场混输原油凝点估算新方法［J］. 技术与应用，2011（09）：45-48.

［3］ 陈俊，张劲军，张帆.计算混合原油凝点的一种新方法［J］. 石油大学学报（自然科学版），2003（05）：76-80.

［4］ 蒋文学.新疆混合原油凝点、粘度计算模型研究及其应用［D］. 北京：中国石油大学（北京），2005.

［5］ 罗会玖，李静，王义，等. 中洛管道混合原油凝点和粘度的测量与计算［J］ . 油气储运， 2010，30（2）：141-143+159.

［6］ 刘天佑，孙维中，高艳清，徐诚.多组分混合原油常温输送技术［J］.油气储运，1999，18（9）：1-7.

［7］ 刘天佑，张秀杰，徐诚.新疆混合原油凝固点的计算［J］. 油气储运，1993，12（2）：37- 42，45.

［8］ 徐诚，张秀杰，刘天佑.多组分混合原油凝点与粘度的图示方法［J］.油气田地面工程，1995，14（2）：16-18.

The Calculation Method of Pour Point of Mixed Crude Oil of Suecuo Oil Pipeline

WANG Qian-nan1, ZHANG Hai-tao2, SIMA Ying-jie3, WANG Jia-nan1, DONG liang-chen1, ZHOU gang1
（1. College of Petroleum Engineering, Northeast Petroleum University, Heilongjiang Daqing 163318，China；2. Storage and Transportation Sales Branch of Daqing Oil Field, Heilongjiang Daqing 163318，China; 3. Natural Gas Branch of Daqing Oil Field, Heilongjiang Daqing 163318，China )

The pour point of mixed oil of Hulun Buir oil and Tamtsag oil under different mixing ratio was tested, and the pour point was calculated by different mixed oil pour point models, suitable calculation model of mixed oil pour point was determined. Through analysis of the experimental data, model updating by curve fitting and least square method, calculation formula of Suecuo oil pipeline mixed crude oil pour point was obtained, and the revised models and fitted curve were verified. The experimental data show that the modified model is more accurate than curve fitting formula for calculating pour point of mixed crude oil. The minimum average absolute deviation of the crude oil pour point reduces 75 percent ,the maximum average absolute deviation of the crude oil pour point reduces 99 percent, the minimum standard deviation reduces 45.77 percent, the maximum average standard deviation reduces 75.26 percent than the existing models.

Suecuo; mixed crude oil; pour point calculation; mathematical model

5　结 论

TE 832

A

1671-0460（2016）05-1065-04

严寒地区高含蜡原油储存工艺方案优化技术研究，项目号：2014D-5006-0607

2016-01-12

王倩楠（1992-），女，辽宁锦州人，2010年毕业于东北石油大学油气储运工程专业，研究方向：原油流变。E-mail：471470840@qq.com。