输电线路覆冰时导线表面形状对碰撞系数的影响
张暕何青(华北电力大学能源动力与机械工程学院 北京 102206)
输电线路覆冰时导线表面形状对碰撞系数的影响
张暕何青
(华北电力大学能源动力与机械工程学院北京102206)
输电线路覆冰是过冷却水滴与导线碰撞并被捕获的物理过程。在计算其碰撞系数时,通常采用外表面为圆形的简化模型代替实际绞合导线模型,这在一定程度上降低了计算的精确性。以流体力学理论为基础,运用Fluent软件模拟了过冷却水滴与简化模型和实际模型发生碰撞的过程,通过对比分析了导线表面形状对空气速度、水滴速度和轨迹以及碰撞系数的影响。结果表明,相同条件下,与简化模型相比,实际模型导线周围的空气速度更小,水滴速度也更小,绕流现象更加明显,轨迹也更向外部扩张,实际模型的碰撞系数更小。因此,为保证覆冰模型的精确性,应该使用绞合导线的实际模型进行计算。
输电线路覆冰碰撞系数表面形状
0 引言
积聚在物体表面的水分因温度过低而冻结成冰的现象是一种分布相当广泛的自然现象,当这种现象发生在输电线路上时称为输电线路覆冰[1]。经验表明,覆冰已经严重危及了输电线路的安全运行[2-4]。当输电线路发生覆冰时,冰的重量会增加导线的张力和其支撑结构的负载,从而使得杆塔弯曲、扭转或者下沉,严重时甚至会造成倒杆、倒塔等事故;相邻档导线的不均匀覆冰会产生张力差,使得导线在线夹内不断滑动,造成外层铝线的磨损;在风激励的作用下,覆冰导线的舞动会造成金具损坏、导线断股等事故[5-10]。
自1932年首次记录覆冰事故以来,各国学者对覆冰机理进行了大量研究。覆冰的形成首先是由气象条件决定的,在温度、湿度及风速等达到一定条件后,才有可能形成覆冰[11]。具备了一定的气象条件后,空气中的过冷却水滴在风力的作用下一部分会绕过导线,一部分会与导线表面发生碰撞并被捕获,这是由流体力学的相关定律所决定。被捕获的水滴在导线表面冻结成冰,与导线和空气进行着热量的交换,这与传热学的知识有关。综合来说,输电线路覆冰是一个包括气象学、流体力学和传热学等多学科的复杂物理现象[12]。
传热学观点认为,覆冰是一个热量传递、交换的过程,其覆冰量、冰的形状等与热平衡状态有关。文献[13]首次运用传热学理论分析了覆冰过程的热现象。文献[14,15]对导线表面覆冰时的传热过程进行了分析,建立了覆冰表面的热平衡方程。文献[16]考虑了碰撞水滴动能、热传导及电流焦耳热等对覆冰过程的影响,完善了原有的热平衡方程。
流体力学观点认为,覆冰是过冷却水滴被导线捕获的过程。由于水滴具有惯性,在经过导线表面时,水滴的流动方向会发生改变。水滴与导线碰撞的幅度与导线直径的比定义为碰撞系数[17]。文献[18]对水滴经过圆柱表面的轨迹进行了数值解析。文献[19]首次采用量纲分析法导出了碰撞系数的无因次准则方程式。随着计算机技术的不断发展,各种计算水滴轨迹和碰撞系数的软件也应运而生(如Lewice、Fensap-ice、Fluent等[20,21]),其模拟结果也得到了试验验证。其中,Fluent由于在计算流体力学方面的先天优势而被广泛采用[22,23]。
目前,高压输电线路通常采用绞合导线输电,其表面由多段相切的圆弧组成,并不是光滑、规则的圆形。但在使用Fluent模拟水滴轨迹时,通常采用圆形表征导线的外截面,并没有考虑导线表面形状的影响,这降低了水滴轨迹和碰撞系数的准确性。因此,本文模拟了实际导线表面形状和相同外径的圆形表面两种情况下空气运动的速度场和水滴的轨迹,计算了对应的碰撞系数,通过对比分析了导线表面形状对碰撞系数的影响。
1 导线型号
用于高压输电的导线种类很多,有铝绞线、铝合金绞线、铝合金芯铝绞线、铝包钢芯铝绞线、钢芯铝绞线、钢芯高强度铝合金绞线等十几种型号,实际最常用的是钢芯铝绞线[24]。钢芯铝绞线是由钢线和铝线绞合而成的,如图1所示。它的内部是钢芯,外部是用铝线通过绞合方式缠绕在钢芯周围。在实际高压输电线路中,铝线截面积为240 mm2、300 mm2、400 mm2的钢芯铝绞线应用最为广泛。因此,本文分别选取这三种型号的钢芯铝绞线进行了计算,其具体参数如表1所示。
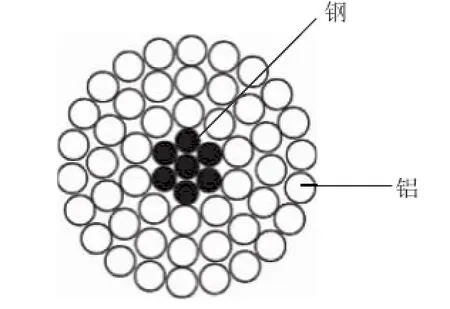
图1 钢芯铝绞线示意图Fig.1 Schematic diagram of aluminium conductor steel reinforced

表1 导线型号参数Tab.1 Mechanical parameters of transmission lines
2 模型建立
2.1物理模型
在进行模拟前,需建立计算区域[25]。由于运动相似性,空气与水滴的流动可以进行降维处理,即视为二维流动。其中,实际模型选取了表1中3种绞合导线,简化模型为与之外径相同的圆形导线。计算区域的外边界为长方形,为减少外边界对流动的影响,各边界长度均取为导线外径的 10倍以上[25]。运用Gambit软件建模和网格划分,为提高计算结果的精确性,导线以及对应入口边界处网格进行加密处理。图2分别为表面为圆表面的简化模型和表面为绞合线的实际模型的网格划分。

图2 模型网格划分Fig.2 Grid division of model
2.2数学模型
目前,在计算覆冰的碰撞系数时,通常采用欧拉-欧拉法或者欧拉-拉格朗日法,其计算的准确性也得到了相关实验的验证[26,27]。由于空气中的过冷却水滴含量很少,即体积分数很低,且远远低于空气,符合多相流中欧拉-拉格朗日方法的前提条件,所以本文采用欧拉-拉格朗日方法进行分析和计算[28]。
将空气视为连续相,在欧拉坐标系下,建立空气相的控制方程。其中,空气的材料属性设置为Fluent默认值,密度为 1.225 kg/m3,运动粘度为 17.9× 10-6kg/(m·s);大气压力为标准气压;入口采用速度边界条件,大小与实际风速一致,由于实际环境中风力一般不会超过6级,即风速不会大于15 m/s,因此本文中风速为0~15 m/s,且均为水平方向[29];出口采用自由流动边界条件;导线采用固体壁面边界条件。求解器为基于压力法的二维非耦合隐式求解器。湍流模型选择标准k-ε模型,对壁面采用标准壁面函数处理。离散方程组采用SIMPLE算法求解。为提高准确度,离散格式采用二阶迎风格式。
将过冷却水滴视为离散相,在拉格朗日坐标系下,建立单个水滴的控制方程,利用离散相模型(Discrete Phase Model,DPM)模拟水滴的流动,得到其运动方程和运动轨迹,实现气液两相流的耦合。其中,水的材料属性设置为 Fluent默认值,密度为998.2 kg/m3,运动粘度为1.003×10-3kg/(m·s);水滴为入口射入,初速度与空气一样,均为风速;水滴中值直径为0~50 μm[29];导线外壁的DPM属性定义为捕获(trap),其余各边界为逃脱(escape)。
建立水滴方程时,假设[30]:
1)水滴在运动过程中保持球形,不分裂、不碰撞、不合并。
2)水滴在运动过程中和周围空气不发生质量、热交换。
3)水滴上的作用力仅有空气粘性阻力、重力和空气浮升力。
3 计算与分析
3.1导线表面形状与空气速度的关系
由于覆冰的形成主要受到与导线方向垂直的水平风的影响,因此为方便计算,本文假设风均水平方向吹入,不存在竖直分量[30],所以空气速度场的分布主要取决于入口风速的大小、导线型号以及导线表面的形状。为科学、严谨地分析导线表面形状与空气速度的关系,本文分别选取了多种大小的入口风速对3种导线进行了模拟计算。
取风速 v分别为 0 m/s、2 m/s、4 m/s、…、12 m/s、15 m/s[31],水平进入,分别对导线简化模型和实际模型进行了模拟。通过分析发现,不同速度和型号下导线表面形状对空气速度的影响十分相似,因此,本文只给出一个典型事例进行分析。图3为入口速度v为6 m/s时,LGJ240-30导线简化模型和实际模型的空气速度云图。
从图3中可以看出,导线表面形状对空气速度有很大的影响,减速效果十分明显。具体地说,在风速大小相同的条件下,与同型号导线的简化模型相比,实际模型导线周围的速度更小,且在导线背风处有很长距离的减速带。如图3所示,在导线左侧即迎风处,简化模型的最小速度在0.5 m/s左右,大部分速度维持在3 m/s左右;而实际模型的最小速度在0.01 m/s左右,大部分速度2 m/s左右。在导线上下两侧,简化模型的速度在8.5 m/s左右,最高速度可达10 m/s以上,而实际模型的速度不到7 m/s,最高速度仅为8 m/s。在导线右侧即背风处,简化模型的最小速度为0.5 m/s左右,并在很短的距离内迅速增大到3 m/s以上,而实际模型的最小速度基本接近于0,并且有很长距离的减速带,其速度在一定距离后才增至3 m/s以上。
由以上分析可知,在风速相同的情况下,与同型号的简化圆形导线相比,实际绞合导线周围的空气速度更小,在导线各侧减速效果都很明显,特别是在背风侧会出现较长的减速带。这主要是由导线表面形状造成的,实际导线的表面并不是一整段连续、光滑的圆弧,而是由多段小圆弧拼接而成,相比较而言,其弧度变化更大,在一定程度上造成了速度的减小。更主要的是,实际导线中存在着多处“V”形夹缝,其对速度的影响很大,空气和过冷却水滴在经过这里时,易形成回流,造成速度的减小。

图3 LGJ-240/30导线简化模型和实际模型空气速度云图(v=6 m/s)Fig.3 Contours of air velocity of simple model and real model of transmission line LGJ-240/30(v=6 m/s)
3.2导线表面形状与水滴速度和运动轨迹的关系
入口风速的大小、水滴中值直径、导线型号及表面形状均影响着水滴的运动。因此,本文分别选取了多种大小的入口风速以及不同大小的水滴中值直径对3种导线进行了模拟计算,为保证计算结果的精确性,与导线外径相对应的入口边界处的网格进行了细化,从此处射入的水滴颗粒数也比两侧更多,水滴轨迹也更密集。
取风速 v分别为 0 m/s、2 m/s、4 m/s、…、12 m/s、15 m/s[29],水滴中值直径d=20 μm,分别对3种导线的简化模型和实际模型进行了模拟。图4为入口速度v为6 m/s的情况下,LGJ240-30导线简化模型和实际模型的过冷却水滴轨迹图。
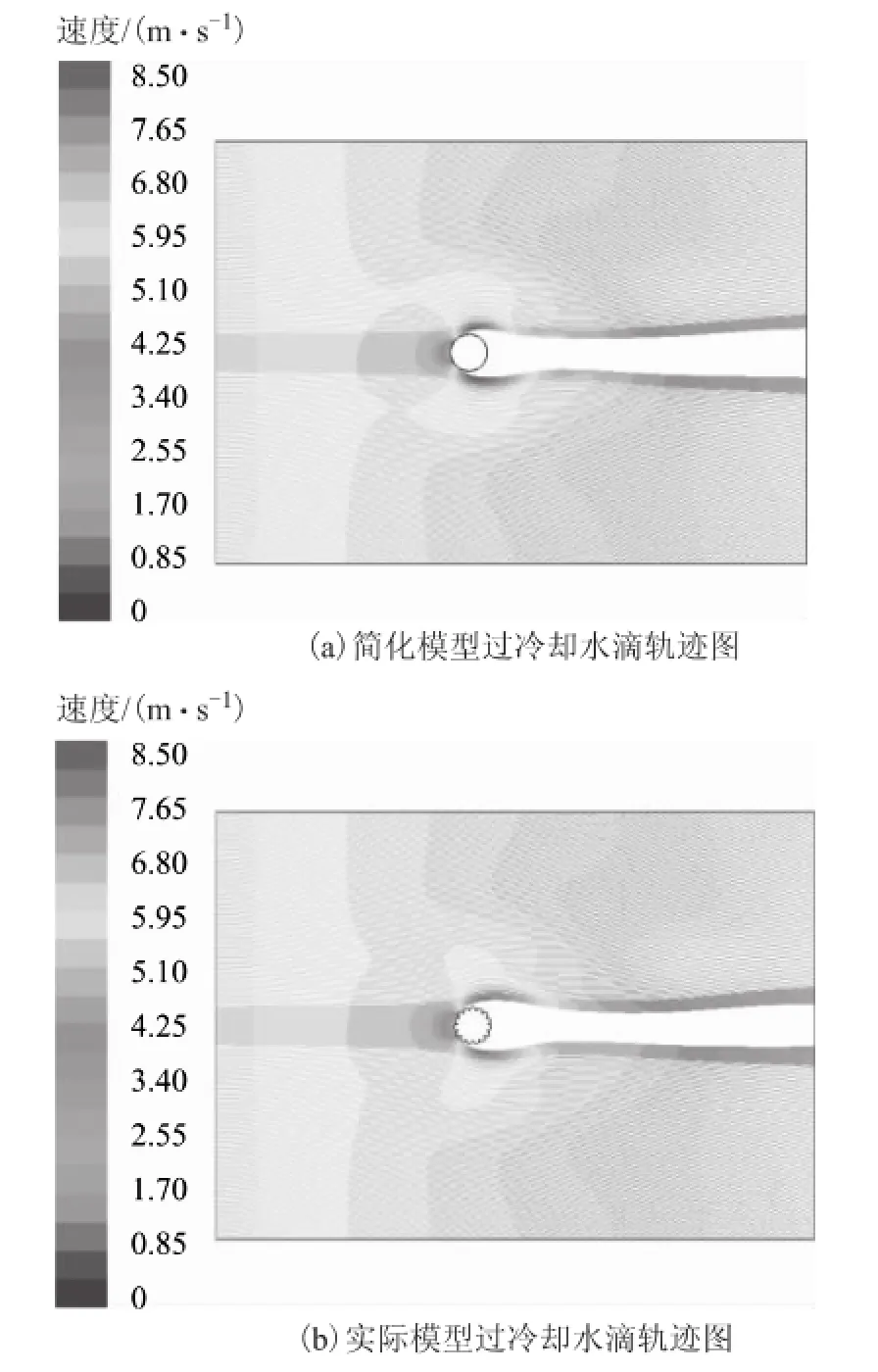
图4 LGJ-240/30导线简化模型和实际模型的过冷却水滴轨迹图(v=6 m/s,d=20 μm)Fig.4 Water droplets trajectories of simple model and real model of the transmission line LGJ-240/30 (v=6 m/s,d=20 μm)
取风速v为10 m/s,水滴中值直径d分别为0 μm、10 μm、…、50 μm,分别对3种导线的简化模型和实际模型进行了模拟。图5为水滴中值直径d=30 μm的情况下,LGJ240-30导线简化模型和实际模型的过冷却水滴轨迹图。
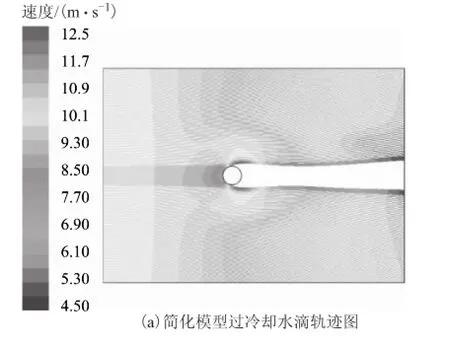

图5 LGJ-240/30导线简化模型和实际模型的过冷却水滴轨迹图(v=10 m/s,d=30 μm)Fig.5 Water droplets trajectories of simple model and real model of the transmission line LGJ-240/30 (v=10 m/s,d=30 μm)
从图4、图5可以看出,虽然两图中风速和水滴中值直径并不相同,但导线表面形状对水滴运动的影响是相似的。与同型号导线的简化模型相比,实际模型中导线周围的水滴速度更小,运动轨迹也不尽相同。以图4为例,简化模型中的过冷却水滴从迎风面进入,一部分水滴与导线发生碰撞,其速度最小为2 m/s,另一部分水滴以4 m/s左右的速度从导线周围绕过,而并未发生碰撞,且在绕过后的最大速度可达到8.5 m/s;而实际模型中与导线碰撞的水滴最小速度仅为0.5 m/s,绕过导线的水滴速度为3 m/s左右,绕过导线后最大速度为7.5 m/s。另外,实际模型的一部分水滴在导线周围时的绕流更明显,轨迹也更向外部扩张,从而并未与导线发生碰撞,这导致实际模型中的碰撞颗粒数和碰撞系数与简化模型并不相同。
显然,与之前的分析类似,表面形状影响着水滴的运动,包括水滴速度场的分布及水滴的运动轨迹,从而导致了实际与导线发生碰撞的水滴颗数与简化模型计算值并不相同,即碰撞系数不同。
3.3导线表面形状与碰撞系数的关系
水滴在经过导线时,大部分会发生绕流现象,并不与导线接触,而一小部分会与导线发生碰撞,通过计算实际与导线碰撞的水滴颗粒数和理论上碰撞的水滴颗粒数的比值即可得到特定外界条件下对应的碰撞系数。通过之前的分析可知,导线表面形状影响着与其碰撞的水滴颗粒数,即影响着碰撞系数的大小,为定量分析表面形状对碰撞系数的影响,本文选取了多种大小的入口风速以及不同大小的水滴中值直径对3种导线进行了模拟计算,结果如表2所示。

表2 不同外界条件下两种模型的碰撞系数值Tab.2 Collision coefficients of two models under different conditions

图6 LGJ-240/30导线简化模型与实际模型碰撞系数的对比图(d=20 μm)Fig.6 Comparison of collision coefficient between simple model and real model of the transmission line LGJ-240/30(d=20 μm)
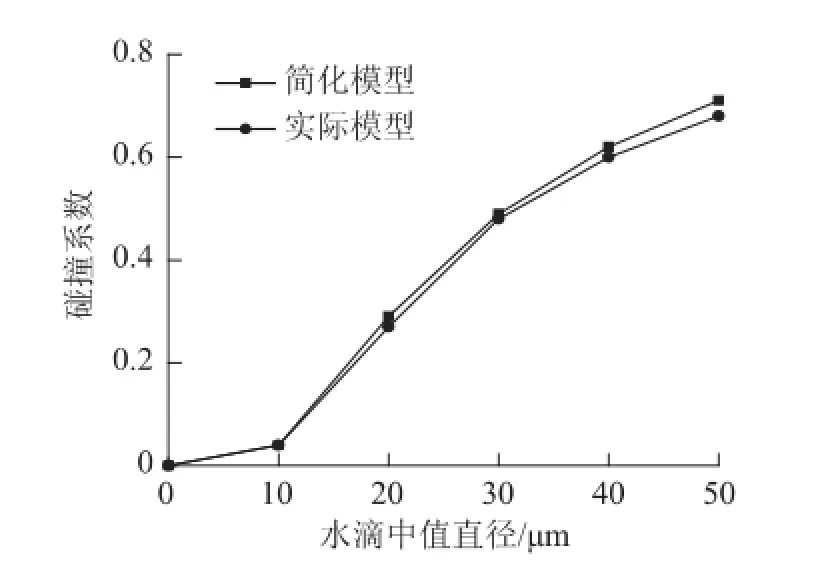
图7 LGJ-240/30导线简化模型与实际模型碰撞系数的对比图(v=10 m/s)Fig.7 Comparison of collision coefficient between simple model and real model of the transmission line LGJ-240/30(v=10 m/s)

图8 不同型号导线简化模型与实际模型碰撞系数的对比图(v=10 m/s,d=30 μm)Fig.8 Comparison of collision coefficient between simple model and real model of different transmission lines (v=10 m/s,d=30 μm)
从表2中可以看出,虽然导线型号、风速以及水滴中值直径并不相同,但导线表面形状对碰撞系数的影响是相似的。图6~图8分别为不同风速、水滴中值直径和导线型号下简化模型与实际模型碰撞系数的对比图。除个别点外,在相同外界条件下,与同型号导线的简化模型相比,实际模型的碰撞系数更小。显然,这是导线表面形状的不同造成的。实际绞合导线不是如简化模型假设的一个光滑的圆,而是由多段圆弧拼接组成,中间存在着很多狭小的夹缝,影响着空气的速度、水滴的速度以及运动轨迹等,同样也影响着与导线碰撞的水滴颗粒数。由于表面形状的不同及这些夹缝的存在,很多在简化模型中可以与导撞的水滴颗粒在实际模型中发生了绕流现象,并未接触到导线,从而导致了碰撞颗粒数和碰撞系数的减小。因此,在计算时若采用简化模型,则会造成一定的误差。以图6为例,在风速从0 m/s增大到15 m/s的过程中,除风速为12 m/s这一点外,简化模型的碰撞系数一直大于实际模型,当风速为4 m/s时,简化模型和实际模型的碰撞系数分别为0.12、0.10,绝对误差约为0.02,相对误差则高达16.7%。
目前,国际通用的计算单位长度导线覆冰增长量公式为[1]

式中,w为空气中液态水含量,kg/m3;v为风速,m/s;A为表面积,m2;α1、α2、α3分别为碰撞系数、捕获系数和冻结系数。捕获系数是指在冻结前仍停留在导线表面的过冷却水滴与碰撞到导线表面的所有过冷却水滴之比。当水滴与导线表面发生碰撞时,大部分都不会反弹,只有小水滴会离开导线表面,但这个量很小,对覆冰过程的影响可以忽略不计[1,32]。因此,液态的水滴一般可以认为没有反弹,即α2=1。冻结系数是指在导线上发生冻结的过冷却水滴与与导线发生碰撞并被捕获的过冷却水滴之比。其大小是由导线表面的热量交换程度决定的,根据现有的热平衡方程[33]即可计算特定条件下的冻结系数。
当v=10 m/s时,LGJ-240/30导线两种模型碰撞系数的差值为0.02,分别取环境温度T=-10℃,液态水含量w=0.001 8 kg/m3,档距L=300 m,捕获系数α2=1,则计算可以得到冻结系数α3=0.817,表面积A=πRL=π×0.010 8×300=10.17 m2。因此,由于碰撞系数误差而造成的覆冰增长率误差为

由此可见,由于碰撞系数误差造成的瞬时覆冰增长率误差高达10.8 kg/h,严重影响了覆冰模型的精确性。导线覆冰是一个长期的过程[14],而在导线表面全覆冰之前,这种由于导线的表面形状而造成的误差将一直存在,影响着覆冰预测结果的准确性。因此,在计算覆冰模型时,当风速较小时,可以采用同外径的圆形截面代替实际绞合导线,而当风速较大时。应该采用表面为绞合线的实际模型,这样才能保证计算结果的精确性。
4 结论
本文以流体力学相关知识为基础,通过Fluent软件分别模拟了过冷却水滴与实际绞合导线和相同外径简化圆形导线两种模型发生碰撞的过程,具体结论如下:
1)在其他参数相同的条件下,与简化模型相比,实际模型导线周围的空气速度更小,即导线表面形状对速度有一定的影响,在导线各侧的减速效果都很明显,且在背风侧的减速带距离更长。
2)在其他参数相同的条件下,导线表面影响过冷却水滴的运动。与简化模型相比,实际模型中导线周围的水滴速度更小,绕流现象更加明显,轨迹也更向外部扩张,从而并未与导线发生碰撞,导致实际模型中的碰撞颗粒数和碰撞系数与简化模型并不相同。
3)在其他参数相同的条件下,与简化模型相比,实际模型的碰撞系数更小。在计算覆冰增长率时,若采用简化模型会产生很大的误差。因此,为保证覆冰模型的精确性,应该使用绞合导线的实际模型进行计算。
[1]Farzameh M.Atmospheric icing of power networks[M]. Berlin:Springer Science&Business Media,2008: 1-10.
[2]胡琴,袁伟,舒立春,等.电压类型对复合绝缘子覆冰及闪络特性的影响[J].电工技术学报,2015,30(3):268-276.
Hu Qin,Yuan Wei,Shu Lichun,et al.Influence of voltage types on composite insulator icing and flashover characteristics[J].Transactions of China Electrotechnical Society,2015,30(3):268-276.
[3]黄文焘,邰能灵,范春菊.基于杆塔结构力学测量的线路覆冰在线监测系统研究[J].电力系统保护与控制,2012,40(24):71-75.
Huang Wentao,Tai Nengling,Fan Chunju.Study on icing monitoringsystemofdifferenttoweroverhead transmission lines based on mechanics measurements [J].Power System Protection and Control,2012,40 (24):71-75.
[4]张满,蒋兴良,舒立春,等.混合凇对分裂导线起晕电压影响[J].电工技术学报,2015,30(3): 258-267.
Zhang Man,Jiang Xingliang,Shu Lichun,et al.The influences of mixed-phase ice on corona inception voltage ofbundleconductor[J].TransactionsofChina Electrotechnical Society,2015,30(3):258-267.
[5]张暕,何青,蓝澜,等.高压输电线路热力融冰影响因素的分析[J].中南大学学报(自然科学版),2013,44(增1):449-455.
Zhang Jian,He Qing,Lan Lan,et al.Analysis of influence factors of thermal de-icing of high-voltage transmission line[J].Journal of Central South University (Science and Technology),2013,44(S1):449-455.
[6]王燕,皇甫成,杜志叶,等.覆冰情况下输电线路有限元计算及其结构优化[J].电力系统保护与控制,2016,44(8):99-106.
Wang Yan,Huangfu Cheng,Du Zhiye,et al.Finite element calculation and structural optimization method for the high voltage transmission line under icing condition [J].Power System Protection and Control,2016,44 (8):99-106.
[7]朱斌,潘玲玲,邹扬,等.考虑融冰因素的输电线路覆冰故障概率计算[J].电力系统保护与控制,2015,43(10):79-84.
Zhu Bin,PanLingling,ZouYang,etal.Fault probability calculation of transmission line considering ice melting factors[J].Power System Protection and Control,2015,43(10):79-84.
[8]何青,吕锡锋,赵晓彤.激励条件下高压输电线路除冰技术应用研究[J].中国电机工程学报,2014,34(18):2997-3003.
He Qing,Lü Xifeng,Zhao Xiaotong.Research on applicationofde-icingtechnologyonhighvoltage transmission line under the condition of incentive[J]. Proceedings of the CSEE,2014,34(18):2997-3003.
[9]陈金熠,范春菊,胡天强,等.考虑架空输电线路状态的线路覆冰监测系统的研究[J].电力系统保护与控制,2012,40(15):93-98.
Chen Jinyi,Fan Chunju,Hu Tianqiang,et al.Study onmonitoringsystemoftransmissionlineicing considering the state of overhead transmission lines[J]. Power System Protection and Control,2012,40(15): 93-98.
[10] 许俊,郭耀杰,曹珂,等.考虑多档导线及绝缘子串影响的覆冰及脱冰输电导线找形分析[J].电工技术学报,2015,30(13):87-91.
Xu Jun,Guo Yaojie,Cao Ke,et al.Research on form-finding of icing and ice-shedding transmission line considering the influence of multi-span and insulator string[J].Transactions of China Electrotechnical Society,2015,30(13):87-91.
[11] 黄宵宁,许瑞,许家浩.南方山区线路覆冰在线监测数据特征分析与预测模型研究[J].电力系统保护与控制,2015,43(23):111-116.
Huang Xiaoning,Xu Rui,Xu Jiahao.Analysis of the characteristics for on-line monitoring data and research of the forecast model of the line icing in southern mountain area[J].Power System Protection and Control,2015,43(23):111-116.
[12]段晓丽.输电线路覆冰量计算模型研究[D].太原:太原理工大学,2010.
[13]Messinger B L.Equilibrium temperature of an unheated icing surface as a function of air speed[J].Journal of the Aeronautical Sciences,2012,20(1):29-42.
[14]Makkonen L.Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology,1984,23 (6):929-939.
[15]Makkonen L.Models for the growth of rime,glaze,icicles and wet snow on structures[J].Philosophical TransactionsoftheRoyalSocietyofLondonA: Mathematical,PhysicalandEngineeringSciences,2000,358(1776):2913-2939.
[16]张志劲,黄海舟,蒋兴良,等.交流输电导线覆冰增长及临界防冰电流的试验研究[J].高电压技术,2012,38(2):469-475.
Zhang Zhijin,Huang Haizhou,Jiang Xingliang,et al. Experiment research on the icing accretion and its critical anti-icing current for conductors under AC condition[J]. High Voltage Engineering,2012,38(2):469-475.
[17]蒋兴良,肖丹华,陈凌,等.基于界面移动理论的导线覆冰过程分析[J].高电压技术,2011,37(4): 982-989.
Jiang Xingliang,Xiao Danhua,Chen Ling,et al. Physical process of icing on fixed wires by interface movement theory[J].High Voltage Engineering,2011,37(4):982-989.
[18]Langmuir I,Blodgett K.A mathematical investigation of water droplet trajectories[J].Collected Works of Irving Langmuir,1946,10(26),348-393.
[19]刘和云,付俊萍,周迪,等.导线覆冰时收集系数的量纲分析[J].华中科技大学学报,2001,29 (10):76-77.
Liu Heyun,Fu Junping,Zhou Di,et al.Dimensional analysis of the collection coefficient wire covered by ice [J].Journal of Huazhong University of Science and Technology,2001,29(10):76-77.
[20]Fu P,Farzaneh M,Bouchard G.Two dimensional modeling of the ice accretion process on transmission line wires and conductors[J].Cold Regions Science and Technology,2006,46(2):132-146.
[21] 郝艳捧,刘国特,阳林,等.风力机组叶片覆冰数值模拟及动载荷特性研究[J].电工技术学报,2015,30(10):292-300.
Hao Yanpeng,Liu Guote,Yang Lin,et al.Study on ice numerical simulation and its power loss characteristics for the blades of wind turbine[J].Transactions of China Electrotechnical Society,2015,30(10):292-300.
[22] 张志劲,黄海舟,蒋兴良,等.基于流体力学的不同型式绝缘子覆冰增长过程分析[J].电工技术学报,2012,27(10):35-43.
Zhang Zhijin,Huang Haizhou,Jiang Xingliang,et al. Analysis of ice growth on different type insulators based onfluiddynamics[J].TransactionsofChina Electrotechnical Society,2012,27(10):35-43.
[23] 肖良成,李新民,江俊.四分裂新月形覆冰导线的气动绕流特性分析[J].电工技术学报,2014,29 (12):261-268.
Xiao Liangcheng,Li Xinmin,Jiang Jun.Study on aerodynamic characteristics of quad-bundled crescentshapeicedconductors[J].TransactionsofChina Electrotechnical Society,2014,29(12):261-268.
[24]黄建辉.架空输电线路常用导线的比较和选择[J].电力建设,2001,22(9):31-32.
Huang Jianhui.Comparison and selection of conventional conductor of overhead transmission lines[J].Electric Power Construction,2001,22(9):31-32.
[25] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004:160-172.
[26]Wirogo S,Srirambhatla S.An Eulerian method to calculate the collection efficiency on two and three dimensional bodies[J].AIAA paper,2003,1073.
[27] 张志劲,黄海舟,蒋兴良,等.复合绝缘子雾凇覆冰厚度预测模型[J].电工技术学报,2014,29(6): 318-326.
Zhang Zhijin,Huang Haizhou,Jiang Xingliang,et al. Model for predicting thickness of rime accreted on compositeinsulators[J].TransactionsofChina Electrotechnical Society,2014,29(6):318-326.
[28] 韩占忠,王敬,兰小平.流体工程仿真计算实例与应用[M].2版.北京:北京理工大学出版社,2010: 273-304.
[29] 蒋兴良,申强.环境参数对导线覆冰厚度影响的试验分析[J].高电压技术,2010,36(5):1096-1100.
Jiang Xingliang,Shen Qiang.Experimental research on influence of environmental parameters on conductor icing thickness[J].HighVoltageEngineering,2010,36 (5):1096-1100.
[30]肖丹华.基于多相流理论的导线覆冰过程研究[D].重庆:重庆大学,2011.
[31]潘晓春,王作民.架空输电线路气象条件设计标准刍议[J].中国电机工程学报,2012(增1):50-56.
Pan Xiaochun,Wang Zuomin.Discussion on the design standardofmeteorologicalconditionsforoverhead transmission line[J].Proceedings of the CSEE,2012 (S1):50-56.
[32]杨军,谢真珍.电线积冰物理过程与数值模拟研究进展[J].气象,2011,37(9):1158-1165.
Yang Jun,Xie Zhenzhen.Advances of study on physical processesandmodelingoficeaccretiononwires [J].Meteorological Monthly,2011,37(9):1158-1165.
[33]孙才新,蒋兴良,熊启新,等.导线覆冰及其干湿增长临界条件分析[J].中国电机工程学报,2003,23(3):141-145.
Sun Caixin,JiangXingliang,XiongQixin,etal. Analysis of critical icing conditions of conductor and wetdry growth[J].Proceedings of the CSEE,2003,23 (3):141-145.
张暕男,1990年生,博士研究生,研究方向为输电线路覆冰及除冰技术。
E-mail:keith0808@163.com(通信作者)
何青男,1962年生,教授,博士生导师,研究方向为电力设备状态监测与故障诊断。
E-mail:hqng@163.com
Influence of Conductor Surface Shape on Collision Coefficient During Transmission Line Icing
Zhang JianHe Qing
(School of Energy Power and Mechanical EngineeringNorth China Electric Power University Beijing102206China)
Icing on the transmission lines is a physical process in which super-cooled water droplets collide with the conductors and then are trapped.Instead of the real model,the simple one which has a circular section is usually used in the calculation of the collision coefficient,which reduces the accuracy of the calculation.Based on the fluid mechanics,the collision processes between the water droplets and both the real model and the simple model are simulated by the computational fluid dynamics software Fluent and the influences of the conductor surface shape on the velocities of air and droplets,the droplets trajectory,and the collision coefficient are analyzed.The results show firstly that,compared with the simple model,the air velocity of the real model is smaller.Secondly,the real model has a smaller droplets velocity,a more obvious streaming,and a more outward droplets trajectory.Finally,the collision coefficient of the real model is always smaller than that of the simple model.Therefore,the real model should be used in order to ensure the accuracy of the icing model.
Transmission lines,icing,collision coefficient,surface shape
TM726
中央高校基本科研业务专项资金(2015XS93)资助项目。
2015-05-14改稿日期 2015-08-26

